文章目录
- 前言
- 一、3 DOF Helicopter实验装置
- 二、3 DOF Helicopter模型建立及简化
- 2.1模型建立
- 2.1.1 俯仰轴建模
- 2.1.2 横侧轴建模
- 2.1.3 旋转轴建模
- 2.2 模型简化
- 三、控制器设计
- 四、实验验证
- 4.1实验设计(包括多实验方法设计及编程实现)
- 4.1.1跟踪信号参数给定
- 4.1.2自适应反步法算法实现
- 4.2实验结果
- 4.2.1仿真实验
- 4.2.2物理装置实验
- 4.2.3三自由度无人机实验视频
前言
本文采用的实验装置为QUANSER公司的3 DOF Helicopter。
使用自适应反步法对其进行控制。
一、3 DOF Helicopter实验装置
3-DOF直升机系统的直升机本体包括支座、螺旋桨、平衡件等,实物如图2-1所示。平衡杆可绕支座在水平面内做旋转动作,在竖直面内做俯仰动作。螺旋桨和平衡块分别被安装在平衡杆的两个端点。两个螺旋桨电机在转动时会形成向上的举力,使平衡杆绕支点俯仰,如果两个电机存在转速差时平衡杆将绕支点做转动。

由于该直升机是二输入三输出的系统,二输入分别为两个电机的电压,三输出分别为:俯仰角、横侧角(滚转角)、旋转角,因此该系统为欠驱动系统。本实验的控制目标是为该被控对象设计一个控制系统,来跟踪和调节三自由度直升机俯仰角和旋转角,从而实现直升飞机飞行高度(俯仰角)和飞行速度的有效控制。
二、3 DOF Helicopter模型建立及简化
2.1模型建立
2.1.1 俯仰轴建模

俯仰轴运动考虑的是横梁在垂直轴上直升机本体在螺旋桨电机的作用下的升降运动,如上图,当前后向伺服电机产生的升力 在垂直方向的分力和 大于直升机本体重力时,直升机机身上升,反之直升机机身下降。根据力学原理,可得俯仰轴微分方程:
J
e
⋅
ε
¨
=
l
1
K
f
⋅
cos
(
ρ
)
(
V
f
+
V
b
)
−
m
g
l
a
cos
(
ε
)
\mathrm{J}_{e} \cdot \ddot{\varepsilon}=l_{1} K_{f} \cdot \cos (\rho)\left(V_{f}+V_{b}\right)-m g l_{a} \cos (\varepsilon)
Je⋅ε¨=l1Kf⋅cos(ρ)(Vf+Vb)−mglacos(ε)
其中,
α
\alpha
α 为俯仰角,
α
¨
\ddot{\alpha}
α¨ 俯仰角的运动加速度,
V
f
V_{f}
Vf,
V
b
V_{b}
Vb 为前后电机输入电压, Mw 为平衡块的质量, Mm 为固定有螺旋桨轴的有效等价质量,
J
ε
J_{\varepsilon}
Jε 为俯仰轴转动 惯量,
J
ε
=
M
w
⋅
L
w
2
+
M
m
⋅
L
w
2
,
l
1
J_{\varepsilon}=M w \cdot L w^{2}+M m \cdot L w^{2}, l_{1}
Jε=Mw⋅Lw2+Mm⋅Lw2,l1 为直乔机本体到支点的距离, Lw 为平衡 块到支点之间的距离,
K
f
K_{f}
Kf 为伺服电机的升力常数,
m
g
l
a
cos
(
ε
)
m g l_{a} \cos (\varepsilon)
mglacos(ε) 为机身的有效重量。
2.1.2 横侧轴建模
横侧轴运动是有两个螺旋桨电机产生的升力差来控制的,当两台螺旋桨电机升力差等于0的时候,横侧轴不偏转,处于水平状态,当升力差存在时,横侧轴发展倾斜,产生横侧运动,横侧轴示意图如下图所示。该模型假定在设计时两台螺旋桨完全对称且对应的伺服电机也是完全相同的,所以在建模的时候可以不考虑重力影响,当两台螺旋桨电机的升力不一样的时候,螺旋桨本体产生一个侧向力造成横侧运动,依据力学原理可以得到该平台的横侧轴微分运动方程如下:
J
p
⋅
ρ
¨
=
K
f
⋅
l
h
⋅
(
V
f
−
V
b
)
J_{p} \cdot \ddot{\rho}=K_{f} \cdot l_{h} \cdot\left(V_{f}-V_{b}\right)
Jp⋅ρ¨=Kf⋅lh⋅(Vf−Vb)

其中,
ρ
\rho
ρ 为横侧角,
ρ
¨
\ddot{\rho}
ρ¨ 为横侧角加速度,
F
1
F_{1}
F1,
F
2
F_{2}
F2 为前后向螺旋桨电机产生的升力
l
h
l_{h}
lh 为螺旋桨伺服电机到中心点的距离;
m
m
m 为螺旋桨伺服电机有效质量。
2.1.3 旋转轴建模
转轴运动的主要动力来源为横侧运动,由于横侧运动,使得两台螺旋桨电机与水平轴成一定角度,产生旋转运动,旋转轴示意图如下图所示。考虑到旋转角、俯仰角、横侧角之间的关系,由拉格朗日力学原理可以得到旋转轴运动微分方程如下:
J
λ
⋅
λ
¨
=
K
f
⋅
l
a
⋅
sin
ρ
⋅
sin
(
ε
)
⋅
(
V
f
+
V
b
)
+
K
f
⋅
l
h
⋅
cos
(
ε
)
(
V
f
−
V
b
)
J_{\lambda}\cdot \ddot{\lambda}=Kf\cdot la\cdot \sin \rho \cdot \sin\mathrm{(}\varepsilon )\cdot \left( V_f+V_b \right) +Kf\cdot lh\cdot \cos\mathrm{(}\varepsilon )\left( V_f-V_b \right)
Jλ⋅λ¨=Kf⋅la⋅sinρ⋅sin(ε)⋅(Vf+Vb)+Kf⋅lh⋅cos(ε)(Vf−Vb)

式中,
λ
\lambda
λ 为旋转角;
J
λ
J_{\lambda}
Jλ 为旋转角转动惯量。
可见,旋转角运动是个与其他两个自由度高度耦合的变量,表现出强非线性,不易于直接用简单的控制算法进行控制。
2.2 模型简化
由模型表达式可知上述分析中建立的数学模型各变量之间具有耦合关系,系统表现出强非线性,很难直接设计有效的控制器,并且发现模型存在两个不同的系统输入,所以为了利用反步法进行控制器设计,我们根据输入的不同将模型拆分为两个子系统,一部分为俯仰轴模型,另一部分为旋转轴与横滚轴模型。
- 俯仰轴模型:
由俯仰轴模型发现参数跟系统输入相乘,所以无法利用自适应办法解决,但是参数与控制输入无关,故采用自适应方法对该参数进行逼近,所以将俯仰轴模型写为以下下形式:
J
e
⋅
ε
¨
=
l
1
K
f
⋅
cos
(
ρ
)
(
V
f
+
V
b
)
−
θ
cos
(
ε
)
\mathrm{J}_e\cdot \ddot{\varepsilon}=l_1K_f\cdot \cos\mathrm{(}\rho )\left( V_f+V_b \right) -\theta \cos\mathrm{(}\varepsilon )
Je⋅ε¨=l1Kf⋅cos(ρ)(Vf+Vb)−θcos(ε) - 旋转轴与横滚轴模型:
由于该部分模型存在严重的耦合,故结合直升机模型飞行姿态,做出可容许范围内的假设。考虑到稳态时实际直升机飞行,横滚角不宜过大,我们假设
∣
ρ
∣
⩽
20
°
\left| \rho \right|\leqslant 20\degree
∣ρ∣⩽20°,
ε
≈
90
°
\varepsilon \approx 90\degree
ε≈90° ,则有
sin
(
ε
)
≈
1
\sin \left( \varepsilon \right) \approx 1
sin(ε)≈1 ,
sin
(
ρ
)
≈
ρ
\sin \left( \rho \right) \approx \rho
sin(ρ)≈ρ ,
cos
(
ρ
)
≈
1
\cos \left( \rho \right) \approx 1
cos(ρ)≈1 ,由于方程中系数都直接与控制输入相乘,所以不采用自适应方法进行逼近,这样可以把上述后两个自由度子系统微分方程简化如下:
J
p
⋅
ρ
¨
=
K
f
⋅
l
h
(
u
f
−
u
b
)
J
t
⋅
λ
¨
=
K
f
⋅
l
a
⋅
sin
p
⋅
(
u
f
+
u
b
)
=
K
ρ
∙
ρ
\begin{aligned} J_p\cdot \ddot{\rho}&=K_f\cdot \mathrm{lh}\left( u_f-u_b \right) \\ J_t\cdot \ddot{\lambda}&=Kf\cdot la\cdot \sin p\cdot \left( u_f+u_b \right) =K\rho \bullet \rho \end{aligned}
Jp⋅ρ¨Jt⋅λ¨=Kf⋅lh(uf−ub)=Kf⋅la⋅sinp⋅(uf+ub)=Kρ∙ρ
其中
K
ρ
K\rho
Kρ 为俯仰角为90°的时候旋转轴方向的动力矩。
根据以上思路,将模型写为如下形式:
x
˙
1
=
x
2
x
˙
2
=
a
⋅
cos
(
x
3
)
(
u
f
+
u
b
)
−
θ
⋅
cos
(
x
1
)
x
˙
3
=
x
4
x
˙
4
=
−
b
x
5
x
˙
5
=
x
6
x
˙
6
=
c
(
u
f
−
u
b
)
\begin{aligned} & \dot{x}_1=x_2 \\ &\dot{x}_2=\mathrm{a}\cdot \cos \left( x_3 \right) \left( u_f+u_b \right) -\theta \cdot \cos \left( x_1 \right) \\ &\dot{x}_3=x_4 \\ &\dot{x}_4=-bx_5 \\ &\dot{x}_5=x_6 \\ &\dot{x}_6=c\left( u_f-u_b \right) \end{aligned}
x˙1=x2x˙2=a⋅cos(x3)(uf+ub)−θ⋅cos(x1)x˙3=x4x˙4=−bx5x˙5=x6x˙6=c(uf−ub)
其中,
x
=
[
ε
,
ε
˙
,
ρ
,
ρ
˙
,
λ
,
λ
˙
]
x=\left[ \varepsilon ,\dot{\varepsilon},\rho ,\dot{\rho},\lambda ,\dot{\lambda} \right]
x=[ε,ε˙,ρ,ρ˙,λ,λ˙],
a
=
0.0858
a=0.0858
a=0.0858,
b
=
1.2304
b=1.2304
b=1.2304,
c
=
0.581
c=0.581
c=0.581。
三、控制器设计
根据整理出的模型,我们设
u
1
=
u
f
+
u
b
u_1=u_f+u_b
u1=uf+ub ,
u
2
=
u
f
−
u
b
u_2=u_f-u_b
u2=uf−ub 。得出如下模型
x
˙
1
=
x
2
x
˙
2
=
a
⋅
cos
(
x
3
)
u
1
−
θ
⋅
cos
(
x
1
)
x
˙
3
=
x
4
x
˙
4
=
−
b
x
5
x
˙
5
=
x
6
x
˙
6
=
c
u
2
\begin{aligned} &\dot{x}_1=x_2 \\ &\dot{x}_2=\mathrm{a}\cdot \cos \left( x_3 \right) u_1-\theta \cdot \cos \left( x_1 \right) \\ &\dot{x}_3=x_4 \\ &\dot{x}_4=-bx_5 \\ &\dot{x}_5=x_6 \\ &\dot{x}_6=cu_2 \end{aligned}
x˙1=x2x˙2=a⋅cos(x3)u1−θ⋅cos(x1)x˙3=x4x˙4=−bx5x˙5=x6x˙6=cu2
然后定义坐标变换:
e
1
=
x
1
−
r
e_1=x_1-r
e1=x1−r ,
e
2
=
x
2
−
x
2
d
e_2=x_2-x_2d
e2=x2−x2d ,
e
3
=
x
3
−
r
1
e_3=x_3-r_1
e3=x3−r1 ,
e
4
=
x
4
−
x
4
d
e_4=x_4-x_4d
e4=x4−x4d ,
e
5
=
x
5
−
x
5
d
e_5=x_5-x_5d
e5=x5−x5d ,
e
6
=
x
6
−
x
6
d
e_6=x_6-x_6d
e6=x6−x6d ,其中
r
r
r为
x
1
x_1
x1 目标输出曲线,
x
2
d
x_2d
x2d 是理想的
x
1
x_1
x1子系统输入,
r
1
r_1
r1为
x
3
x_3
x3目标输出曲线,
x
4
d
、
x
5
d
、
x
6
d
x_4d\text{、}x_5d\text{、}x_6d
x4d、x5d、x6d分别是理想的
x
3
x_3
x3子系统输入。
第1步 尝试使用Lyapunov函数如下
V
1
=
1
2
e
1
2
\mathrm{V}_1=\frac{1}{2}e_{1}^{2}
V1=21e12
对
V
1
\mathrm{V}_1
V1求导可以得到
V
2
=
e
1
e
˙
1
=
e
1
(
x
2
−
r
˙
)
\begin{aligned} \mathrm{V}_2&=e_1\dot{e}_1 \\ \,\, &=e_1\left( x_2-\dot{r} \right) \end{aligned}
V2=e1e˙1=e1(x2−r˙)
设计虚拟控制函数
x
2
d
=
−
k
1
e
1
+
r
˙
,
k
1
>
0
x_2d=-k_1e_1+\dot{r},k_1>0
x2d=−k1e1+r˙,k1>0,将
x
2
d
x_2d
x2d带入到上式中,可以得到
V
˙
=
−
k
1
e
1
2
+
e
1
e
2
\dot{\mathrm{V}}=-k_1e_{1}^{2}+e_1e_2
V˙=−k1e12+e1e2。
第2步 尝试使用Lyapunov函数如下
V
2
=
V
1
+
1
2
e
2
2
+
1
2
θ
~
2
\mathrm{V}_2=\mathrm{V}_1+\frac{1}{2}e_{2}^{2}+\frac{1}{2}\tilde{\theta}^2
V2=V1+21e22+21θ~2
对
V
2
\mathrm{V}_2
V2求导可以得到
V
˙
2
=
V
˙
1
+
e
2
e
˙
2
−
θ
~
θ
˙
=
−
k
1
e
1
2
+
e
1
e
2
+
e
2
(
a
⋅
cos
(
x
3
)
u
1
−
θ
⋅
cos
(
x
1
)
⋅
x
2
d
)
\begin{aligned} \dot{\mathrm{V}}_2&=\dot{\mathrm{V}}_1+e_2\dot{e}_2-\tilde{\theta}\dot{\theta} \\ \,\, &=-k_1e_{1}^{2}+e_1e_2+e_2\left( \mathrm{a}\cdot \cos \left( x_3 \right) u_1-\theta \cdot \cos \left( x_1 \right) \cdot x_2d \right) \end{aligned}
V˙2=V˙1+e2e˙2−θ~θ˙=−k1e12+e1e2+e2(a⋅cos(x3)u1−θ⋅cos(x1)⋅x2d)
得到控制输入
u
1
u_1
u1如下:
u
1
=
−
k
2
e
2
−
e
1
+
θ
~
1
⋅
cos
(
x
1
)
+
x
˙
2
d
a
⋅
cos
(
x
3
)
,
k
2
>
0
u_1=-k_2e_2-e_1+\frac{\tilde{\theta}_1\cdot \cos \left( x_1 \right) +\dot{x}_2d}{\mathrm{a}\cdot \cos \left( x_3 \right)}\text{,}k_2>0
u1=−k2e2−e1+a⋅cos(x3)θ~1⋅cos(x1)+x˙2d,k2>0
将
u
1
u_1
u1带入上式得
V
˙
2
=
−
k
1
e
1
2
−
k
2
e
2
2
−
θ
~
(
e
2
cos
(
x
1
)
+
θ
^
˙
)
\dot{\mathrm{V}}_2=-k_1e_{1}^{2}-k_2e_{2}^{2}-\tilde{\theta}\left( e_2\cos \left( x_1 \right) +\dot{\hat{\theta}} \right)
V˙2=−k1e12−k2e22−θ~(e2cos(x1)+θ^˙)
所以得到自适应参数的变化率为
θ
^
˙
=
−
e
2
cos
(
x
1
)
\dot{\hat{\theta}}=-e_2\cos \left( x_1 \right)
θ^˙=−e2cos(x1)
第3步 尝试使用Lyapunov函数如下
V
3
=
1
2
e
3
2
\mathrm{V}_3=\frac{1}{2}e_{3}^{2}
V3=21e32
对
V
3
\mathrm{V}_3
V3求导可以得到
V
3
=
e
3
e
˙
3
=
e
3
(
x
4
−
r
˙
1
)
\begin{aligned} \mathrm{V}_3&=e_3\dot{e}_3 \\ \,\, &=e_3\left( x_4-\dot{r}_1 \right) \end{aligned}
V3=e3e˙3=e3(x4−r˙1)
设计虚拟控制函数
x
4
d
=
−
k
3
e
3
+
r
˙
,
k
3
>
0
x_4d=-k_3e_3+\dot{r},k_3>0
x4d=−k3e3+r˙,k3>0,将 带入到上式中,可以得到
V
˙
=
−
k
3
e
3
2
−
k
4
e
4
2
−
e
4
e
5
\dot{\mathrm{V}}=-k_3e_{3}^{2}-k_4e_{4}^{2}-e_4e_5
V˙=−k3e32−k4e42−e4e5。
第5步 尝试使用Lyapunov函数如下
V
5
=
V
4
+
1
2
e
5
2
\mathrm{V}_5=\mathrm{V}_4+\frac{1}{2}e_{5}^{2}
V5=V4+21e52
对
V
5
\mathrm{V}_5
V5求导可以得到
V
˙
5
=
V
˙
4
+
e
5
e
˙
5
=
−
k
3
e
3
2
−
k
4
e
4
2
−
k
5
e
5
2
+
e
5
(
x
6
−
x
˙
5
d
)
\begin{aligned} \dot{\mathrm{V}}_5&=\dot{\mathrm{V}}_4+e_5\dot{e}_5 \\ \,\, &=-k_3e_{3}^{2}-k_4e_{4}^{2}-k_5e_{5}^{2}+e_5\left( x_6-\dot{x}_5d \right) \end{aligned}
V˙5=V˙4+e5e˙5=−k3e32−k4e42−k5e52+e5(x6−x˙5d)
设计虚拟控制函数
x
6
d
=
−
k
5
e
5
+
e
4
+
x
5
d
,
k
5
>
0
x_6d=-k_5e_5+e_4+x_5d,k_5>0
x6d=−k5e5+e4+x5d,k5>0,将
x
6
d
x_6d
x6d带入到上式中,可以得到
V
˙
=
−
k
3
e
3
2
−
k
4
e
4
2
−
k
5
e
5
2
+
e
5
e
6
\dot{\mathrm{V}}=-k_3e_{3}^{2}-k_4e_{4}^{2}-k_5e_{5}^{2}+e_5e_6
V˙=−k3e32−k4e42−k5e52+e5e6。
第6步 尝试使用Lyapunov函数如下
V
6
=
V
5
+
1
2
c
e
6
2
\mathrm{V}_6=\mathrm{V}_5+\frac{1}{2c}e_{6}^{2}
V6=V5+2c1e62
对
V
6
\mathrm{V}_6
V6求导可以得到
V
˙
6
=
V
˙
5
+
e
6
e
˙
6
=
−
k
3
e
3
2
−
k
4
e
4
2
−
k
5
e
5
2
+
e
6
(
u
2
−
x
˙
6
d
c
)
\begin{aligned} \dot{\mathrm{V}}_6&=\dot{\mathrm{V}}_5+e_6\dot{e}_6 \\ \,\, &=-k_3e_{3}^{2}-k_4e_{4}^{2}-k_5e_{5}^{2}+e_6\left( u_2-\frac{\dot{x}_6d}{c} \right) \end{aligned}
V˙6=V˙5+e6e˙6=−k3e32−k4e42−k5e52+e6(u2−cx˙6d)
得到控制输入
u
2
u_2
u2如下:
u
2
=
−
k
5
e
6
−
e
5
+
x
˙
6
d
c
,
k
5
>
0
u_2=-k_5e_6-e_5+\frac{\dot{x}_6d}{c}\text{,}k_5>0
u2=−k5e6−e5+cx˙6d,k5>0
稳定性分析
由于
V
=
1
2
e
1
2
+
1
2
a
e
2
2
+
1
2
θ
~
2
+
1
2
e
3
2
+
1
2
b
e
4
2
+
1
2
e
5
2
+
1
2
c
e
6
2
V
˙
=
−
k
1
e
1
2
−
k
2
e
2
2
−
k
3
e
3
2
−
k
4
e
4
2
−
k
5
e
5
2
−
k
6
e
6
2
\begin{aligned} \mathrm{V}&=\frac{1}{2}e_{1}^{2}+\frac{1}{2a}e_{2}^{2}+\frac{1}{2}\tilde{\theta}^2+\frac{1}{2}e_{3}^{2}+\frac{1}{2b}e_{4}^{2}+\frac{1}{2}e_{5}^{2}+\frac{1}{2c}e_{6}^{2} \\ \dot{\mathrm{V}}&=-k_1e_{1}^{2}-k_2e_{2}^{2}-k_3e_{3}^{2}-k_4e_{4}^{2}-k_5e_{5}^{2}-k_6e_{6}^{2} \end{aligned}
VV˙=21e12+2a1e22+21θ~2+21e32+2b1e42+21e52+2c1e62=−k1e12−k2e22−k3e32−k4e42−k5e52−k6e62
所以系统一定是收敛的,并且实现了渐近稳定。
四、实验验证
4.1实验设计(包括多实验方法设计及编程实现)
4.1.1跟踪信号参数给定
本实验分别对正弦信号和方波信号进行了跟踪实验,具体参数设定如下。
对于跟踪的正弦信号,其中俯仰轴所跟踪的正弦信号振幅为7.5°,频率为0.04Hz;旋转轴所跟踪的正弦信号振幅为30°,频率为0.03Hz,具体波形如下图所示。

图4-1原正弦信号
由于正弦信号刚开始的导数不为零,所以为了满足反步法需要的参考信号n阶可导,需要将正弦信号经过Bessel滤波器,使其满足要求。图4-2是经处理后的参考信号(正弦)。

图4-2 Bessel滤波器处理后的正弦信号
对于跟踪的方波信号,其中俯仰轴所跟踪的方波信号振幅为7.5°,频率为0.03Hz;旋转轴所跟踪的方波信号振幅为15°,频率为0.04Hz,具体波形如图4-3所示。 由于反步法要求跟踪信号n阶可导,所以对所需跟踪的方波信号进行处理,本实验首先通过限制方波信号的一阶导数上升沿压摆率和下降沿压摆率降低其斜率,再通过Bessel滤波器使其达到n阶可导的效果。

图 4-3 原方波信号

图 4-4 Rate Limiter处理后的方波信号

图 4-5 Bessel滤波器处理后的方波信号
最后通过搭建simulink实现对信号的处理,具体结构如图4-6所示:
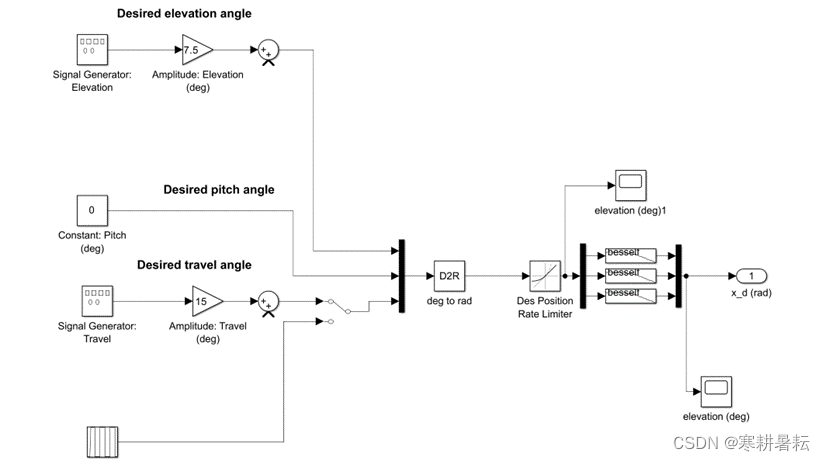
图 4-6 跟踪信号simulink搭建
4.1.2自适应反步法算法实现

图4-7 自适应反步法算法模型搭建
Backstepping controller函数:
function [y,y1] = fcn(u)
k1=2;
k2=3;
k3=2;
k4=2;
k5=3;
k6=3;
r=u(7);
rd=u(8);
rdd=u(9);
r1=u(10);
r1d=u(11);
r1dd=u(12);
r1ddd=u(13);
r1dddd=u(14);
e1=u(1)-r;
x2d=-k1*e1+rd;
e2=u(2)-x2d;
x22d=-k2*(u(2)-rd)+rdd;
e3=u(3)-r1;
x4d=-k3*e3+r1d;
x44d=-k3*(u(4)-r1d)+r1dd;
e4=u(4)-x4d;
x444d=-k3*(-1.2304*u(5)-r1dd)+r1ddd;
x5d=k4*e4+e3-x44d/1.2304;
e5=u(5)-x5d;
x55d=k4*(-1.2304*u(5)-x44d)+u(4)-r1d-x444d/1.2304;
x6d=-k5*e5+e4+x55d;
e6=u(6)-x6d;
x4444d=-k3*(-1.2304*u(6)-r1ddd)+r1dddd;
x555d=k4*(-1.2304*u(6)-x444d)+(-1.2304*u(5)-r1dd)-x4444d/1.2304;
x66d=-k5*(u(6)-x55d)+(-1.2304*u(5)-x44d)+x555d;
asd=-k2*e2-e1+(x22d+u(15)*cos(u(1)))/0.0858/cos(u(3));
fgh=-k6*e6-e5+x66d/0.581;
y = (asd+fgh)/2;
y1 = (asd-fgh)/2;
Adaptive Parameters函数
function y = fcn(u)
k1=2;
th=5;
r=u(7);
rd=u(8);
e1=u(1)-r;
x2d=-k1*e1+rd;
e2=u(2)-x2d;
y = -th*e2*cos(u(1));
4.2实验结果
4.2.1仿真实验
a)当预设的俯仰角和旋转角的跟踪信号为正弦信号时,可以得到如下所示的实验结果。

图 4-8 采用自适应反步法控制器俯仰方向跟踪效果(正弦信号)
!
图 4-9 采用自适应反步法控制器旋转方向跟踪效果(正弦信号))

图 4-10自适应反步法控制器滚转角偏转角度(正弦信号)

图 4-11采用反步法控制器电机输入电压(正弦信号)
b)当预设的俯仰角和的跟踪信号为方波信号时,可以得到如下所示的实验结果。

图 4-12采用自适应反步法控制器俯仰方向跟踪效果(方波信号)

图 4-13采用自适应反步法控制器旋转方向跟踪效果(方波信号)

图 4-14自适应反步法控制器横滚角偏转角度(方波信号)

图 4-15 采用反步法控制器电机输入电压(方波信号)
4.2.2物理装置实验
a)当预设的俯仰角和旋转角的跟踪信号为正弦信号时,可以得到如下所示的实验结果。

图 4-25 采用反步法控制器俯仰方向跟踪效果(正弦信号)

图 4-27 采用反步法控制器旋转方向跟踪效果(正弦信号)

图 4-29 采用反步法控制器滚转角偏转角度(正弦信号)

图 4-31 采用反步法控制器电机输入电压(正弦信号)

图 4-32 自适应反步法自适应参数变化(正弦信号)
4.2.3三自由度无人机实验视频
3 DOF Helicopter backstrpping
仿真以与实验程序文件
本文内容由网友自发贡献,版权归原作者所有,本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容,请联系:hwhale#tublm.com(使用前将#替换为@)