本文介绍如何用数学语言对实际中的优化问题进行建模. 通过建立数学模型, 我们利用现成的求解器可以便捷地计算出最优解(或可行解).
考虑三个粮食储量分别是100, 200, 300的仓库 (单位:吨, 下文省略). 我们需要把粮食运送给4个客户, 其需求分别是: 120, 60, 270, 150.
仓库到客户的单位运输成本用矩阵
C
C
C描述:
[
350
200
300
250
220
330
300
270
215
230
290
240
]
\begin{aligned} \begin{bmatrix} 350 & 200 & 300 & 250 \\ 220 & 330 & 300 & 270 \\ 215 & 230 & 290 & 240 \\ \end{bmatrix} \end{aligned}
⎣⎡350220215200330230300300290250270240⎦⎤
其中行代表仓库, 列代表客户. 矩阵中的每一个值代表对应的仓库到客户的单位运输成本. 我们的目标最小化总的运输成本.
下面我们用数学语言描述该问题.
输入
输出
下面我们写出问题的目标和约束.
目标是最小化总的运输成本, 即
min
∑
i
,
j
c
i
j
x
i
j
.
\min \sum_{i,j}c_{ij}x_{ij}.
mini,j∑cijxij.
我们需要满足的约束条件有两个:
综上所述, 我们可以把运输问题用线性规划(Linear Programming)来表示.
min ∑ i j c i j x i j s.t. ∑ j x i j ≤ a i , ∀ i ∑ i x i j = d j , ∀ j x i j ≥ 0 , ∀ i , j . \begin{aligned} \min~& \sum_{ij}c_{ij} x_{ij} \\ \text{s.t. } & \sum_{j} x_{ij} \leq a_i, \forall i \\ & \sum_{i} x_{ij} = d_j, \forall j \\ & x_{ij} \geq 0, \forall i, j. \end{aligned} min s.t. ij∑cijxijj∑xij≤ai,∀ii∑xij=dj,∀jxij≥0,∀i,j.
为了更加直观地写出数学模型, 我们可以总结一份标准的指南. 它包含四个基本步骤:
指标(Indices)
指标的作用是主要为了简化记号. 以上述运输问题为例, 我们的指标有
i
i
i和
j
j
j, 其中
i
i
i代表仓库,
j
j
j代表客户.
参数(Parameters)
参数是问题的输入. 以上述运输问题为例, 我们的参数是: 供给量(
s
i
s_i
si), 需求量(
d
j
)
d_j)
dj), 单位运输成本
c
i
,
j
c_{i,j}
ci,j.
决策变量(Decision Variables)
决策变量是算法的输出.
优化目标(Objective)
一般是最小化或最大化一个目标函数. 在某些情况下, 问题只需要找到一个可行解, 因此也可以不指定优化目标.
约束(Constraints)
用等式或不等式描述解的限制.
常用的商用求解器有Gruobi和CPLEX(可申请教育和学术的lisense). 商用求解器功能强大, 能求解多种类型的规划问题, 例如整数规划, 混合整数规划, 二次规划等. 免费的求解器有Google的ORtools, 它把一些开源的求解器做了集成, 求解速度虽然比不上商用求解器, 实际中也能满足很多业务需求.
求解方式有两种:
第一种是直接用商用求解器提供的IDE. 按照求解器的建模语法把模型写出来, 然后求解. 建模语法的好处是非常贴近公式化的描述, 所见即所得.
第二种是调用求解器提供的API, 初始化参数, 约束, 目标, 然后求解.
本文我们使用开源工具ORtools求解(基本的教程请自行google,需要翻墙)
模型
# model.py
from ortools.linear_solver import pywraplp
import numpy as np
class TransportModel(object):
def __init__(self, a, d, C):
"""
:param a: 供给量(m维向量), m代表仓库数量
:param d: 需求量(n维向量), n代表客户数量
:param C: 单位运输成本(m*n维矩阵), C[i][j]代表仓库i到客户j的单位运输成本
"""
self._solver = pywraplp.Solver('TransportModel',
pywraplp.Solver.GLOP_LINEAR_PROGRAMMING)
self._a = a
self._d = d
self._C = C
self._m = len(self._a) # 仓库数量
self._n = len(self._d) # 客户数量
self._x = None # 决策变量
self._solution_x = None # 计算结果
self._obj_val = None # 目标函数值
def _init_decision_variables(self):
self._x = [
# 0 <= x[i][j] <= infinity
[self._solver.NumVar(0, self._solver.infinity(), "x[%d][%d]" % (i, j))
for j in range(self._n)] for i in range(self._m)
]
def _init_constraints(self):
# 每个仓库的出库量不能超过其供给量
# sum(x[i][j]) <= a[i], over j
for i in range(self._m):
ct = self._solver.Constraint(0, self._a[i])
for j in range(self._n):
ct.SetCoefficient(self._x[i][j], 1)
# 每个客户的需求应该被满足
# sum(x[i][j]) == b[j], over i
for j in range(self._n):
ct = self._solver.Constraint(self._d[j], self._d[j])
for i in range(self._m):
ct.SetCoefficient(self._x[i][j], 1)
def _init_objective(self):
obj = self._solver.Objective()
for i in range(self._m):
for j in range(self._n):
obj.SetCoefficient(self._x[i][j], self._C[i][j])
obj.SetMinimization()
def solve(self):
self._init_decision_variables()
self._init_constraints()
self._init_objective()
self._solver.Solve()
# 求解器返回的解
self._solution_x = [
[self._x[i][j].solution_value() for j in range(self._n)]
for i in range(self._m)
]
# sum(C[i][i] * x[i][j]) over i,j
self._obj_val = np.sum(np.array(self._C) * np.array(self._solution_x))
def print_result(self):
print("最优值 = ", self._obj_val)
print("最优解 x = ")
print(np.array(self._solution_x))
主函数
# main.py
from data import a, d, C # 运输问题实例
from model import TransportModel
if __name__ == '__main__':
tm = TransportModel(a, d, C)
tm.solve()
tm.print_result()
完整代码: 运输问题
把数字1-9填入下图的空格子中, 且满足如下三个条件:
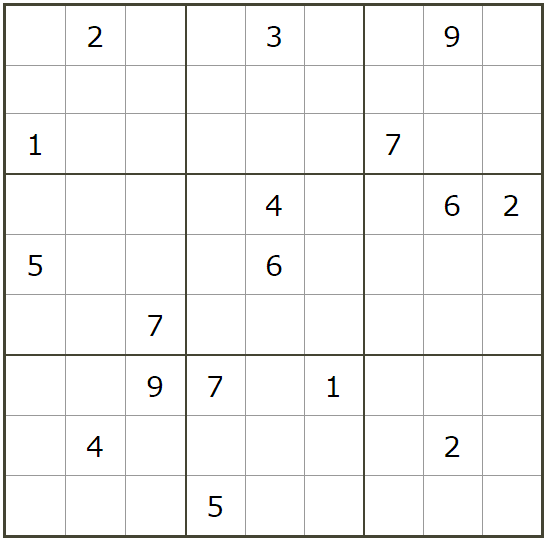
我们通过数学规划的方式求解该问题.
指标
参数
决策变量
约束
综上所述, 我们的规划可以写成下面的整数规划(Integer Programming). 注意: 无优化目标.
min 0 s.t. x i , j , p , q , n ≥ a i , j , p , q , n , ∀ i , j , p , q , n ∑ n x i , j , p , q , n = 1 , ∀ i , j , p , q ∑ p , q x i , j , p , q , n = 1 , ∀ i , j , n ∑ j , q x i , j , p , q , n = 1 , ∀ i , p , n ∑ i , p x i , j , p , q , n = 1 , ∀ j , q , n x i , j , p , q ∈ { 0 , 1 } . \begin{aligned} \min~& 0 \\ \text{s.t. } & x_{i,j,p,q,n} \geq a_{i,j,p,q,n}, \forall i, j,p,q, n \\ & \sum_n x_{i,j,p,q,n} = 1, \forall i,j,p,q \\ & \sum_{p, q} x_{i,j, p, q, n} = 1, \forall i, j, n \\ & \sum_{j, q} x_{i,j,p,q,n} = 1, \forall i,p, n \\ & \sum_{i, p} x_{i,j,p,q,n} = 1, \forall j,q, n \\ & x_{i,j,p,q} \in \{ 0,1\} . \end{aligned} min s.t. 0xi,j,p,q,n≥ai,j,p,q,n,∀i,j,p,q,nn∑xi,j,p,q,n=1,∀i,j,p,qp,q∑xi,j,p,q,n=1,∀i,j,nj,q∑xi,j,p,q,n=1,∀i,p,ni,p∑xi,j,p,q,n=1,∀j,q,nxi,j,p,q∈{0,1}.
模型
# model.py
from ortools.linear_solver import pywraplp
import numpy as np
class SudokuModel(object):
def __init__(self, a):
"""
:param a: Sudoku实例
"""
self._solver = pywraplp.Solver('SudokuModel',
pywraplp.Solver.BOP_INTEGER_PROGRAMMING)
self._a = a
self._x = None # 决策变量
self._solution_x = None # 计算结果
def __init_decision_variables(self):
self._x = np.empty((3, 3, 3, 3, 9)).tolist()
for i in range(3):
for j in range(3):
for p in range(3):
for q in range(3):
for n in range(9):
# 已知数字不允许修改
# x[i][j][p][q][n] >= a[i][j][p][q][n]
self._x[i][j][p][q][n] \
= self._solver.IntVar(self._a[i][j][p][q][n], 1,
'x[%d][%d][%d][%d][%d]' % (i, j, p, q, n))
def __init_constraints(self):
# 一个单元格同时只允许填入一个数字
# sum(x[i][j][p][q][n]) = 1, over n
for i in range(3):
for j in range(3):
for p in range(3):
for q in range(3):
ct = self._solver.Constraint(1, 1)
for n in range(9):
ct.SetCoefficient(self._x[i][j][p][q][n], 1)
# 每个区块包含数字1-9
# sum(x[i][j][p][q][n]) = 1, over p, q
for i in range(3):
for j in range(3):
for n in range(9):
ct = self._solver.Constraint(1, 1)
for p in range(3):
for q in range(3):
ct.SetCoefficient(self._x[i][j][p][q][n], 1)
# 每行包含数字1-9
# sum(x[i][j][p][q][n]) = 1, over j, q
for i in range(3):
for p in range(3):
for n in range(9):
ct = self._solver.Constraint(1, 1)
for j in range(3):
for q in range(3):
ct.SetCoefficient(self._x[i][j][p][q][n], 1)
# 每列包含数字1-9
# sum(x[i][j][p][q][n]) = 1, over i, p
for j in range(3):
for q in range(3):
for n in range(9):
ct = self._solver.Constraint(1, 1)
for i in range(3):
for p in range(3):
ct.SetCoefficient(self._x[i][j][p][q][n], 1)
def solve(self):
self.__init_decision_variables()
self.__init_constraints()
self._solver.Solve()
self._get_solution_x()
def _get_solution_x(self):
self._solution_x = np.empty((3, 3, 3, 3))
for i in range(3):
for j in range(3):
for p in range(3):
for q in range(3):
for n in range(9):
if self._x[i][j][p][q][n].solution_value() == 1:
self._solution_x[i][j][p][q] = n + 1
def print_result(self):
res = np.empty((9, 9))
for i in range(3):
for p in range(3):
for j in range(3):
for q in range(3):
res[i*3+p][j*3+q] = self._solution_x[i][j][p][q]
print(res)
主函数
# main.py
from model import SudokuModel
from data import a
if __name__ == '__main__':
sm = SudokuModel(a)
sm.solve()
sm.print_result()
完整代码: Sudoku