提取ORB特征后,需要根据点估计相机的运动。根据相机的原理,可以分为下面几种情况:
1、当采用单目相机,只知道2D像素坐标,需要根据两组2D点估计运动,这时用对极几何求解
2、当采用双目相机、RGB-D相机,或者通过其他方法知道距离信息,需要根据两组3D点估计运动,这时用ICP求解
3、如果是一组3D点、一组2D点(也就是得到了一些3D点和它们在相机的投影位置),这时用PnP求解
1、对极约束
当希望求取两帧图像  之间的运动,设第一帧到第二帧的运动为
之间的运动,设第一帧到第二帧的运动为 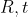 。两个相机中心分别为
。两个相机中心分别为  。现在,考虑
。现在,考虑 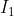 中有一个特征点
中有一个特征点 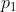 ,它在
,它在 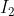 中对应着特征点
中对应着特征点 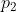 。这两个点是通过特征匹配得到的。如果匹配正确,说明它们确实是同一个空间点在两个成像平面上的投影
。这两个点是通过特征匹配得到的。如果匹配正确,说明它们确实是同一个空间点在两个成像平面上的投影
为了描述它们之间的几何关系,用到了极平面、极点、基线、极线等概念
极平面:  所在的平面
所在的平面
极点: 连线与像平面
连线与像平面  的交点
的交点 
基线: 连线
连线
极线:极平面与两个像平面  之间的相交线
之间的相交线
从第一帧的角度上看,射线  是某个像素 P 可能出现的空间位置,如果不知道 P 的位置,那么当我们在第二个图像上看时,极线
是某个像素 P 可能出现的空间位置,如果不知道 P 的位置,那么当我们在第二个图像上看时,极线  是 P 可能出现的投影位置,也是射线
是 P 可能出现的投影位置,也是射线  在第二个相机中的投影。当我们通过特征点匹配,确定了
在第二个相机中的投影。当我们通过特征点匹配,确定了 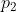 的像素位置,从而能够推断 P 的空间位置以及相机运动
的像素位置,从而能够推断 P 的空间位置以及相机运动

设 ![P = [X,Y,Z]^T](https://latex.codecogs.com/gif.latex?P%20%3D%20%5BX%2CY%2CZ%5D%5ET) ,
, ,
, (R,t描述第一个坐标系到第二个坐标系的运动)
(R,t描述第一个坐标系到第二个坐标系的运动)
由于 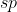 和
和  都位于同一条投影直线上,因此记
都位于同一条投影直线上,因此记 
投影关系改写为  ,
,
将P的归一化坐标  代入上式得
代入上式得 
两边同时左乘 t^ (相当于两侧同时与 t 做外积),
两侧同时左乘  ,
,  ,
, 与
与  均垂直,因此式子左边等于 0 ,从而
均垂直,因此式子左边等于 0 ,从而 
将 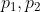 代入上式,
代入上式,
上面两个式子称为对极约束,它的几何意义是  共面,其中
共面,其中
 是本质矩阵
是本质矩阵
 是基础矩阵
是基础矩阵
对极约束又表示为 
对极约束给出了匹配点对的空间位置关系。相机位姿估计问题变为以下两步:
1、根据像素位置求解 E 或 F (本质矩阵 E 与基础矩阵 F 相差了相机内参 K ,而 K 在SLAM问题中是已知的,因此求解 E 和求解 F 是一样的)
2、根据 E 或 F ,求解 R ,t
2、本质矩阵
本质矩阵是3x3矩阵,具有以下特点:
1、在不同尺度下是等价的。本质矩阵 E 由对极约束定义,对极约束是等式为0的约束,因此对 E 乘以任意非0常数后,对极约束仍然成立
2、本质矩阵的内在性质:由  ,本质矩阵 E 的奇异值必定是
,本质矩阵 E 的奇异值必定是 ![[\sigma ,\sigma ,0] ^T](https://latex.codecogs.com/gif.latex?%5B%5Csigma%20%2C%5Csigma%20%2C0%5D%20%5ET) 的形式
的形式
3、 共有六个自由度,由于尺度等价性,实际上只有五个自由度(线性无关)
共有六个自由度,由于尺度等价性,实际上只有五个自由度(线性无关)
由于本质矩阵 E 具有五个自由度,因此至少使用 5 对点求解。但是,E 的内在性质是一种非线性性质,在求解线性方程时会带来麻烦,因此,也可以只考虑它的尺度等价性,使用八对点来估计 E (八点法)。八点法只利用了 E 的线性性质,因此可以在线性代数框架下求解
考虑一对匹配点,它们的归一化坐标为:![x_1 = [u_1 ,v_1 ,1]^T , x_2 = [u_2 ,v_2 ,1]^T](https://latex.codecogs.com/gif.latex?x_1%20%3D%20%5Bu_1%20%2Cv_1%20%2C1%5D%5ET%20%2C%20x_2%20%3D%20%5Bu_2%20%2Cv_2%20%2C1%5D%5ET) ,根据对极约束
,根据对极约束

把矩阵 E 展开,写成向量的形式:![e = [e_1 ,e_2 ,e_3 ,e_4 ,e_5 ,e_ 6 ,e_7 ,e_8 ,e_9 ]^T](https://latex.codecogs.com/gif.latex?e%20%3D%20%5Be_1%20%2Ce_2%20%2Ce_3%20%2Ce_4%20%2Ce_5%20%2Ce_%206%20%2Ce_7%20%2Ce_8%20%2Ce_9%20%5D%5ET) ,那么对极约束可以写成
,那么对极约束可以写成 ![[u_1 u_2 ,u_1 v_2 ,u_1 ,v_1 u_2 ,v_1 v_2 ,v_1 ,u_2 ,v_2 ,1] * e = 0](https://latex.codecogs.com/gif.latex?%5Bu_1%20u_2%20%2Cu_1%20v_2%20%2Cu_1%20%2Cv_1%20u_2%20%2Cv_1%20v_2%20%2Cv_1%20%2Cu_2%20%2Cv_2%20%2C1%5D%20*%20e%20%3D%200)
同理,对于其它点对也有相同的表示。把所有点都放到一个方程中,变成线性方程组 (  表示第 i 个特征点)
表示第 i 个特征点)

线性方程组的系数矩阵由特征点位置构成,大小为 8 × 9。如果八对匹配点组成的矩阵满足秩为 8 的条件,那么 E 的各元素就可由上述方程解得,并且零空间维数为 1, e 构成一条线
根据已经估得的本质矩阵 E,恢复出相机的运动 R,t,这个过程是由奇异值分解(SVD)得到的:
其中 U,V 为正交阵,Σ 为奇异值矩阵。根据 E 的内在性质,我们知道 
在 SVD 分解中,对于任意一个 E,存在两个可能的 t,R 与它对应:

其中  表示沿 Z 轴旋转 90 度得到的旋转矩阵。同时,由于 −E 和 E 等价,所以对任意一个 t 取负号,也会得到同样的结果。因此,从 E 分解到 t,R 时,一共存在四个可能的解
表示沿 Z 轴旋转 90 度得到的旋转矩阵。同时,由于 −E 和 E 等价,所以对任意一个 t 取负号,也会得到同样的结果。因此,从 E 分解到 t,R 时,一共存在四个可能的解
已知空间点在相机(蓝色线)上的投影(红点),想要求解相机的运动。在保持红点不变的情况下,可以画出四种可能的情况,只有第一种解中,P 在两个相机中都具有正的深度。因此点在两个相机下的深度可以作为正解的判别依据
根据线性方程解出的 E,可能不满足 E 的内在性质——它的奇异值不一定为 σ,σ,0 的形式。这时,在做 SVD 时,会刻意地把 Σ 矩阵调整成上面的样子
对八点法求得的 E 进行 SVD 分解后,会得到奇异值矩阵  ,不妨设
,不妨设  ,取
,取

这相当于是把求出来的矩阵投影到了 E 所在的流形上。当然,更简单的做法是将奇异值矩阵取成  ,因为 E 具有尺度等价性,这样做也是合理的
,因为 E 具有尺度等价性,这样做也是合理的
3、单应矩阵
单应矩阵 H 通常描述处于共同平面上的一些点。若场景中的特征点都落在同一平面上,可以通过单应性来进行运动估计
在图像 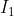 和
和 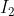 有一对匹配好的特征点
有一对匹配好的特征点 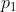 和
和 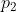 。这些特征点落在某平面上。设这个平面满足方程:
。这些特征点落在某平面上。设这个平面满足方程: ,即
,即 ,则
,则

上式简写为  ,其中 H 就是单应矩阵(3x3)
,其中 H 就是单应矩阵(3x3)
单应矩阵与旋转、平移以及平面参数有关,求解运动与 本质矩阵E 类似,根据匹配点对计算 H ,然后将其分解,计算旋转和平移。上式展开:
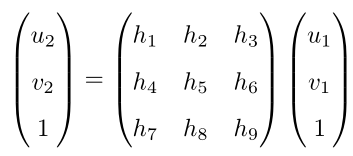
这里的等号是在非零因子下成立的。在实际处理中,通常乘以一个非零因子使得 h 9 = 1。然后根据第三行,去掉这个非零因子,于是有:
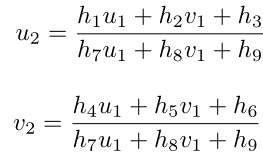
整理后得:

一组匹配点对可以构造出三个约束(只有两个是线性无关的),因此自由度为 8 的单应矩阵可以通过 4 对匹配特征点算出(这些特征点不能有三点共线的情况),即求解以下的线性方程组(当 h 9 = 0 时,右侧为零):

以上做法把 H 矩阵看成了向量,通过解该向量的线性方程来恢复 H,又称直接线性变换法
求出单应矩阵以后需要对其进行分解,才可以得到相应的旋转矩阵 R 和平移向量 t。单应矩阵的分解同样会返回四组旋转矩阵与平移向量,并且同时可以计算出它们分别对应的场景点所在平面的法向量
如果已知成像的地图点的深度全为正值(即在相机前方),则又可以排除两组解。最后仅剩两组解,这时需要通过更多的先验信息进行判断
通常可以通过假设已知场景平面的法向量来解决,如场景平面与相机平面平行,那么法向量 n 的理论值为 
当特征点共面,或者相机发生纯旋转的时候,基础矩阵的自由度下降,出现退化现象。现实中的数据总包含一些噪声,这时候如果继续使用八点法求解基础矩阵,基础矩阵多余的自由度将会主要由噪声决定。为了能够避免退化现象造成的影响,通常我们会同时估计基础矩阵 F 和单应矩阵H,选择重投影误差比较小的那个作为最终的运动估计矩阵
4、三角测量
在单目 SLAM 中,仅通过单张图像无法获得像素的深度信息,需要通过三角测量的方法来估计地图点的深度
三角测量是指:通过在两处观察同一个点的夹角,确定该点的距离。
考虑图像 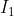 和
和 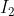 ,以左图为参考,右图的变换矩阵为 T。相机光心为
,以左图为参考,右图的变换矩阵为 T。相机光心为 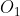 和
和 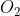 。在
。在 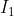 中有特征点
中有特征点 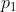 ,对应
,对应 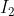 中有特征点
中有特征点 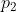 。理论上直线
。理论上直线  与
与  在场景中会相交于一点 P,该点即是两个特征点所对应的地图点在三维场景中的位置
在场景中会相交于一点 P,该点即是两个特征点所对应的地图点在三维场景中的位置
然而由于噪声的影响,这两条直线往往无法相交。因此,可以通过最二小乘去求解

按照对极几何中的定义,设  为两个特征点的归一化坐标,那么它们满足:
为两个特征点的归一化坐标,那么它们满足:
通过对极几何,可以求解出 R,t 。而估计深度,也就是求解上式的
对上式两边左乘  ,得:
,得:
通过这个式子可以解出 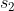 ,进一步可以求出
,进一步可以求出 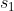 。由于估计的 R,t 不一定能准确使上式为0,因此多采用最小二乘法求解
。由于估计的 R,t 不一定能准确使上式为0,因此多采用最小二乘法求解
本文内容由网友自发贡献,版权归原作者所有,本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容,请联系:hwhale#tublm.com(使用前将#替换为@)