2.1 信息的存储
- 十六进制转二进制,将十六进制的每一位转换成一个4位的二进制
即:
[
0123456789
A
B
C
D
E
F
]
16
[0123456789ABCDEF]_{16}
[0123456789ABCDEF]16 对应
[
0000
−
1111
]
2
[0000-1111]_2
[0000−1111]2
- 每台计算机都有一个字长
(
w
o
r
d
s
i
z
e
)
(word\ size)
(word size),对于一个字长为
w
w
w位的机器,虚拟地址范围为
[
0
,
2
w
−
1
]
[0,2^w-1]
[0,2w−1]
程序最多可以访问
2
w
2^w
2w个字节
- 在当前大规模从32位字长机器到64位字长机器的迁移情况,大部分的64位字长机器都向后兼容了32位字长机器。当程序
prog.c用伪指令linux> gcc -m32 prog.c编译后,该程序就可以在32位或64位机器上正确运行。而当程序prog,c用伪指令linux> gcc -m64 prog.c编译后,该程序只能在64位机器上运行。区别32位和64位程序,区别在于程序是如何编译的,而不是其依赖运行的机器类型。
- 信息的存储方式,以
in a = 4666;为例,a的大小为4个字节,二进制表示为0001 0010 0011 1010,十六进制表示为0x123a。
有效字节从低到高依次为a,3,2,1,这些字节在机器上的存储是连续的,如果最低有效字节a存储在内存地址更高的地方,那么这称为大端(高尾端)。反之最低有效字节a存储在内存地址更低的地方,这称为小段(低尾端)。
至于大端和小端的机器,Linux32, Windows
参考博客
- 如何打印出一个数的具体存储格式
/*
author: solego
*/
#include<bits/stdc++.h>
using namespace std;
typedef unsigned char* byte_pointer;
void show_bytes(byte_pointer start, int len) {
for(int i = 0; i < len; ++i) {
printf("%x\n", start[i]);
} printf("\n");
int main()
{
int x = -10;
/*
expect: 0x ff ff ff f6
x(sign magnitude) = 10000000 00000000 00000000 00001010
x(one's complement) = 11111111 11111111 11111111 11110101
x(two's complement) = 11111111 11111111 11111111 11110110
10(two's complement) = 00000000 00000000 00000000 00001010
*/
show_bytes((byte_pointer) &x, sizeof(x));
return 0;
}
result:
f6
ff
ff
ff
由此可以看出来,在计算机中存储的是补码,循环是从低地址到高地址的,而优先输出最低有效字节,所以windows采用的是小端(低尾端),这里利用unsigned char大小为
1
1
1字节,恰好表示出[0,255]。
| 数据类型 |
移位方向 |
移位方式 |
| 无符号数 |
左移 |
逻辑移位,补0 |
| 有符号数 |
左移 |
逻辑移位,补0 |
| 无符号数 |
右移 |
算术移位,补0 |
| 有符号数 |
右移 |
算术移位,负数补1,其余补0 |
| 左移采用逻辑移位,无符号数的右移采用逻辑移位 |
|
|
| 有符号数采用算术右移,负数右移左补1,其余右移左补0,这也是对应满足补码运算的。 |
|
|
2.2 整数的表示
-
计算机中的整数都是以补码形式存在的
原码,反码和补码:建议参考
将一个数的补码看成向量,向量的每一位为其二进制值,一个
w
w
w位的向量,则有:
对于非负数和无符号数,
∑
i
=
0
w
−
1
x
i
2
i
\sum_{i=0}^{w-1}x_i{2^i}
∑i=0w−1xi2i,
对于负数:其最高位的位权是
−
2
w
−
1
-2^{w-1}
−2w−1,即
x
w
−
1
×
(
−
2
w
−
1
)
+
∑
i
=
0
w
−
2
x
i
2
i
x^{w-1}\times(-2^{w-1})+\sum_{i=0}^{w-2}x_i{2^i}
xw−1×(−2w−1)+∑i=0w−2xi2i
这样来看,就能很好的解释
1000
0000
1000\ 0000
1000 0000表示的是
−
2
7
-2^7
−27而非
−
0
-0
−0了。
以
8
8
8位为例
对于有符号数:
- 正数:符号位为
0
0
0,
[
0000
0000
,
0111
1111
]
[0000\ 0000,0111\ 1111]
[0000 0000,0111 1111] 即
[
0
,
2
7
−
1
]
[0,2^7-1]
[0,27−1]
- 负数:符号位为
1
1
1,
[
1000
0000
,
1111
1111
]
[1000\ 0000,1111\ 1111]
[1000 0000,1111 1111] 即
[
−
2
7
,
−
1
]
[-2^7,-1]
[−27,−1]
-
位数相等的 有符号数和无符号数之间的互相转换
short int a = -12345;
unsigned short b = (unsigned short) a;
printf("a = %d, b = %u", a, b);
result:
a = -12345
b = 53191
以上例子中short和unsigned short均为2字节,即16位
-12345: 1100 1111 1100 0111
53191: 1100 1111 1100 0111
可以发现两者的补码是一致的,可以理解为解释这些二进制位的方式变了
对于有符号数,最高位解释为符号位,同时最高位是
−
2
15
-2^{15}
−215,而对于无符号数,最高位解释为普通的位,即为
2
15
2^{15}
215。
关于
w
w
w位的有符号数到无符号数的映射
如果有符号数的符号位为
0
0
0,那么解释不变
如果有符号数的符号位为
1
1
1,那么在解释成无符号数时,该位就是一个普通的位。
具体到十进制来看:
S
T
o
U
(
x
)
=
{
x
,
x
≥
0
x
+
2
w
,
x
<
0
SToU(x)=\left\{ \begin{aligned} x,x\geq 0\\ x+2^w,x<0\\ \end{aligned} \right.
SToU(x)={x,x≥0x+2w,x<0
这是因为将负数的符号位由
−
2
w
−
1
-2^{w-1}
−2w−1解释为
2
w
−
1
2^{w-1}
2w−1是相差了
2
w
2^w
2w的,而将非负数转换成无符号数,符号位无影响。
从无符号数转换成有符号数:
U
T
o
S
(
x
)
=
{
x
,
x
≤
2
w
−
1
−
1
x
−
2
w
,
x
≥
2
w
−
1
UToS(x)=\left\{ \begin{aligned} x,x\leq 2^{w-1}-1\\ x-2^w,x\geq 2^{w-1}\\ \end{aligned} \right.
UToS(x)={x,x≤2w−1−1x−2w,x≥2w−1
-
在有符号数和无符号数进行运算时,有符号数会被强制转换成无符号数来执行运算
int a = -1;
unsigned int b = 0;
if(a < b) printf("a < b\n");
else printf("a > b\n");
result:
a > b
这里的signed int a被强制转换成了(unsigned int a),即a = 2^32 - 1
-
将位数不相等的整数类型转换
-
从字节少的强制转换成字节多的,扩展的为高位,原有的部分为低位
对无符号数的扩展是零扩展,在扩展的数位上补0即可
对有符号数的扩展是符号位扩展,即在扩展的数位上补符号位
对于数据的强制类型转换,是不可改变其所表示的值的。
int a = -1;
long long b = a;
a: 1111 1111 1111 1111 1111 1111 1111 1111
b: 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111
需要证明这两种补码得到的结果是一样的。
我们考虑一种简单的情况:
a 为4位的-1,b 为5位的-1,c 为6位的-1
a: 1111 = -2^3 + 2^2 + 2^1 + 2^0
b: 1 1111 = (-2^4 + 2^3) + 2^2 + 2^1 + 2^0 = -2^3 + 2^2 + 2^1 + 2^0
c: 11 1111 = (-2^5 + 2^4 + 2^3) + 2^1 + 2^0 = -2^3 + 2^2 + 2^1 + 2^0
因此c = b = a,扩展到更高位依然是正确的
对于正数来说,扩展的符号位为0,显然是不会影响结果的。
-
从字节多的强制转换成字节少的,则是保留低位,直接去除高位,这样是可能改变实际值的
对于无符号数是直接去除高位即可
对于有符号数,先用无符号数解释,然后直接去除高位,再用有符号数来解释
long long b = -1ll << 32;
cout << b << "\n";
int a = (int)b;
cout << a << "\n";
result:
-4294967296
0
2.3 整数的运算 加(减)法
-
无符号数加法
0
≤
x
<
2
w
,
0
≤
y
<
2
w
0\leq x < 2^w, 0\leq y<2^w
0≤x<2w,0≤y<2w
x
+
y
=
{
x
+
y
,
x
+
y
<
2
w
x
+
y
−
2
w
,
x
+
y
≥
2
w
x+y=\left\{ \begin{aligned} x+y,x+y< 2^{w}\\ x+y-2^w,x+y\geq 2^w\\ \end{aligned} \right.
x+y={x+y,x+y<2wx+y−2w,x+y≥2w
大于等于
2
w
2^w
2w相当于溢出,溢出的部分全部被舍弃,只保留
[
0
,
w
)
[0,w)
[0,w)位,相当于对
2
w
2^w
2w取模,因为这里
x
+
y
x+y
x+y的范围是
[
0
,
2
w
+
1
−
2
]
[0,2^{w+1}-2]
[0,2w+1−2],最多只会在第
w
w
w位上有权,所以减去
2
w
2^w
2w即可。
判断溢出
bool add_ok(unsigned x, unsigned y) {
unsigned sum = x + y;
return sum >= x;
}
证明:
数学方面来看:
x + y >= x, x + y >= y
发生溢出时:
sum = x + y - 2^w
因为 y < 2^w
所以y - 2^w < 0
所以 x + y - 2^w < x
对于y是同理。
-
有符号数加法,分为正溢出,即两个正数相加的结果溢出,以及负溢出,即两个负数相加的结果溢出
−
2
w
−
1
≤
x
≤
2
w
−
1
−
1
,
−
2
w
−
1
≤
y
≤
2
w
−
1
−
1
-2^{w-1}\leq x\leq 2^{w-1}-1, -2^{w-1}\leq y\leq 2^{w-1}-1
−2w−1≤x≤2w−1−1,−2w−1≤y≤2w−1−1
x
+
y
=
{
x
+
y
−
2
w
,
x
+
y
≥
2
w
−
1
x
+
y
,
−
2
w
−
1
≤
x
+
y
<
2
w
−
1
x
+
y
+
2
w
,
x
+
y
<
−
2
w
−
1
x+y=\left\{ \begin{aligned} x+y-2^w,x+y\geq 2^{w-1}\\ x+y,-2^{w-1}\leq x+y< 2^{w-1}\\ x+y+2^w,x+y< -2^{w-1}\\ \end{aligned} \right.
x+y=⎩⎪⎨⎪⎧x+y−2w,x+y≥2w−1x+y,−2w−1≤x+y<2w−1x+y+2w,x+y<−2w−1
对于正溢出:
两个二进制正数 127和1:
0111 1111
0000 0001
----------
1000 0000
对于负溢出:
两个二进制负数 -128和-1
1000 0000
1111 1111
----------
(1)0111 1111
无论是哪种:
都可以用无符号数来解释他们,然后进行无符号数的加法
得到结果后,再进行无符号数到有符号数的转换
唯一的问题是:在解释负溢出时,得到了(w+1)位,解释成有符号数则是一个(w+1)位的有符号数,
而我们是舍弃溢出不部分的,所以需要加上这部分,即2^w
-
加法逆元
对于整数
x
x
x,使得
x
+
x
′
=
0
x+x'=0
x+x′=0的
x
′
x'
x′就是
x
x
x的加法逆元,也可以称为相反数
-
无符号数的加法逆元
0
≤
x
<
2
w
,
0
≤
x
′
<
2
w
0\leq x< 2^w,0\leq x'<2^w
0≤x<2w,0≤x′<2w
这里要涉及到溢出求逆元了,当第
w
+
1
w+1
w+1位为
1
1
1,其余均为
0
0
0,特殊的是当
x
=
0
x=0
x=0,
x
′
=
0
x'=0
x′=0
否则
x
′
=
2
w
−
x
x'=2^w-x
x′=2w−x
x
′
=
{
x
,
x
=
0
2
w
−
x
,
x
>
0
x'=\left\{ \begin{aligned} x,x=0\\ 2^w-x,x>0\\ \end{aligned} \right.
x′={x,x=02w−x,x>0
-
有符号数的加法逆元
当
x
>
−
2
w
x>-2^w
x>−2w,那么对应的
x
′
=
−
x
x'=-x
x′=−x
当
x
=
−
2
w
x=-2^w
x=−2w,那么对应的
x
′
=
x
x'=x
x′=x
x
′
=
{
x
,
x
=
−
2
w
−
x
,
x
>
−
2
w
x'=\left\{ \begin{aligned} x,x=-2^w\\ -x,x>-2^w\\ \end{aligned} \right.
x′={x,x=−2w−x,x>−2w
2.3 乘除法
2.4 浮点数
浮点数与其位模式的表示对应为:
V
=
(
−
1
)
s
×
M
×
2
E
V = (-1)^s\times M \times 2^{E}
V=(−1)s×M×2E

最高位
s
s
s 表示符号位,当
s
=
0
s=0
s=0,表示正数;当
s
=
1
s=1
s=1,表示负数
e
x
p
exp
exp 表示阶码,即指数位,与上述的
E
E
E 对应
f
r
a
c
frac
frac与尾数相关,与上述的
M
M
M 对应
浮点数分为单精度浮点数 float 和双精度浮点数 double
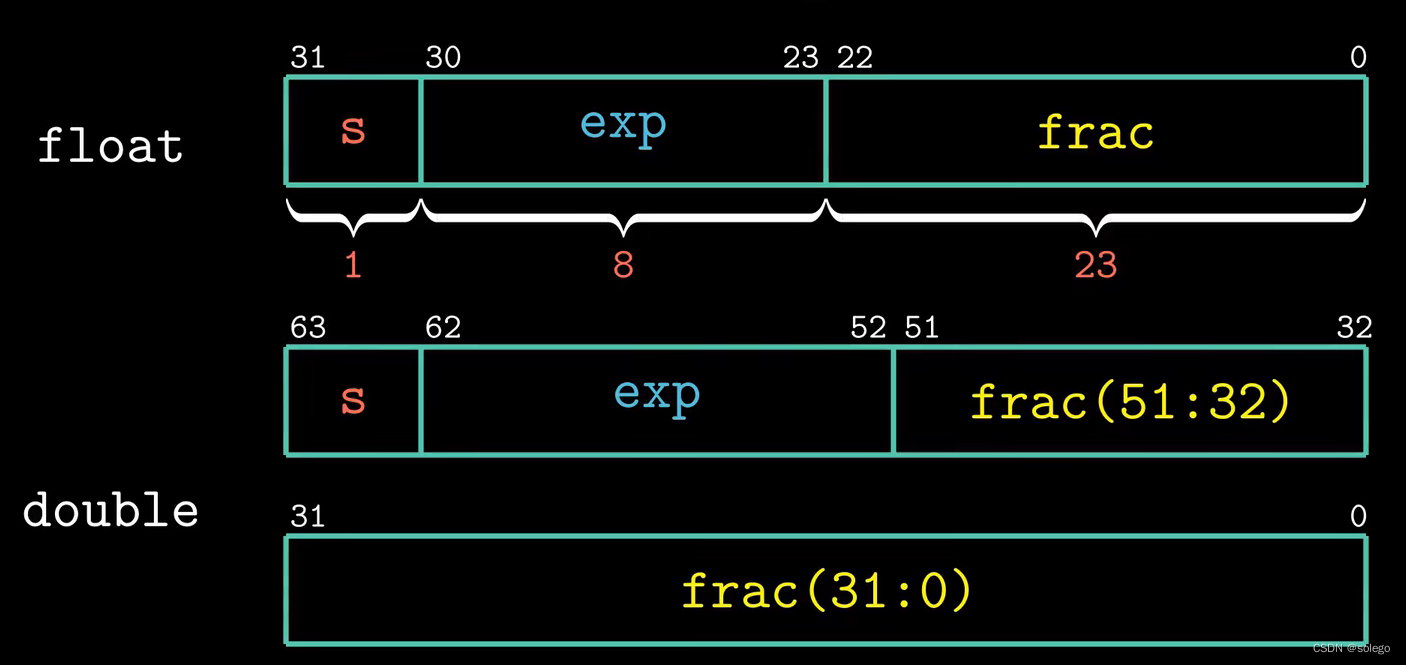
浮点数的值分为三种:
- 规格化的值 (Normalized Values)
- 非规格化的值 (Denormalized Values)
- 特殊值 (Special Values)
阶码的值决定了浮点数的值是以上的哪一种
- 当
e
x
p
exp
exp 的二进制位不全为
0
0
0 或不全为
1
1
1,此时表示的是 规格化的值
- 当
e
x
p
exp
exp 的二进制位全为
0
0
0,此时表示的是非规格化的值
- 当
e
x
p
exp
exp 的二进制位全为
1
1
1,此时表示的是特殊值
特殊值分为两类:
- 一类表示无穷大或无穷小(Infinity):
f
r
a
c
frac
frac 对应的二进制位全为
0
0
0
- 另一类表示不是一个数 (NaN):
f
r
a
c
frac
frac 对应的二进制位不全为
0
0
0
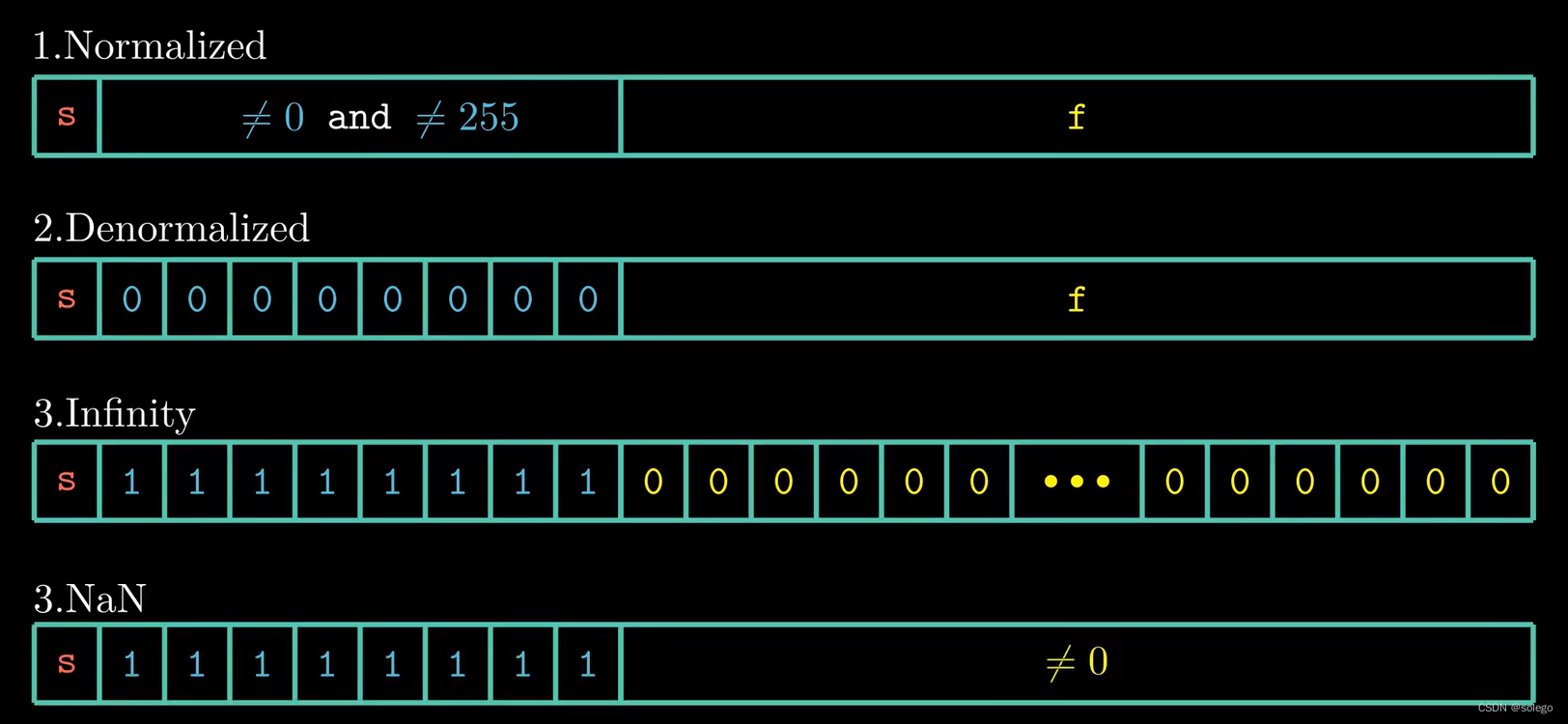
规格化的值(Normalized Values)
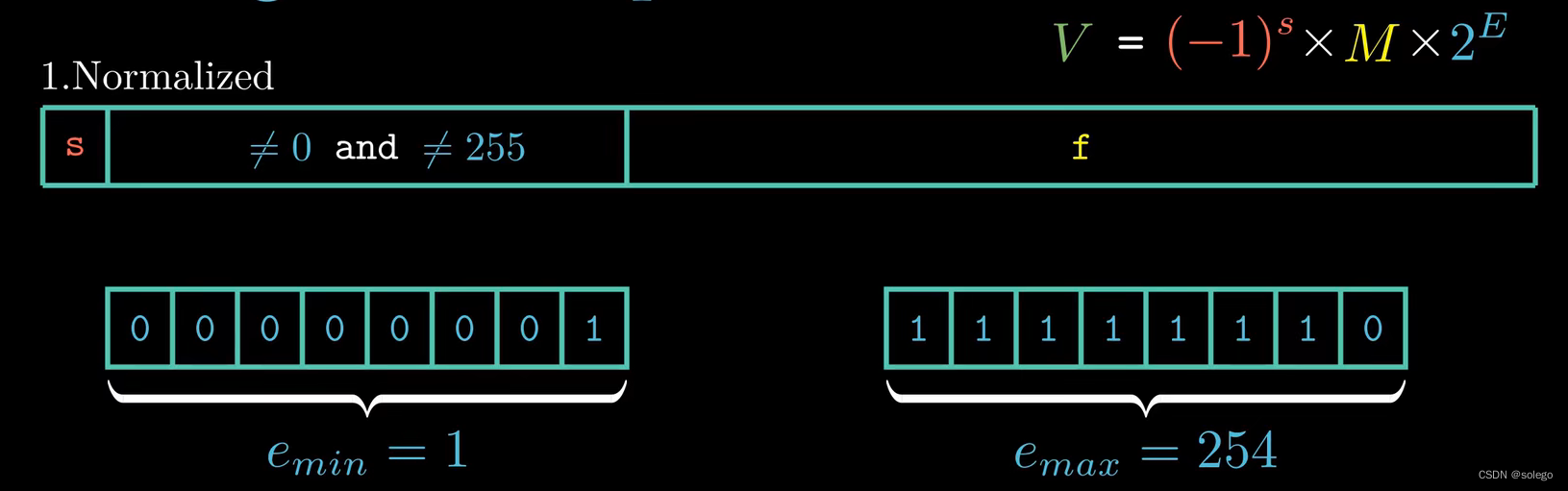
E
=
e
−
b
i
a
s
E = e-bias
E=e−bias
b
i
a
s
(
f
l
o
a
t
)
=
2
8
−
1
−
1
=
127
bias(float)=2^{8-1}-1=127
bias(float)=28−1−1=127
b
i
a
s
(
d
o
u
b
l
e
)
=
2
11
−
1
−
1
=
1023
bias(double)=2^{11-1}-1=1023
bias(double)=211−1−1=1023
对应单精度浮点数
f
l
o
a
t
float
float,
e
m
i
n
=
1
,
e
m
a
x
=
254
e_{min}=1,e_{max}=254
emin=1,emax=254
E
∈
[
−
126
,
127
]
E\in[-126,127]
E∈[−126,127]
对应双精度浮点数
d
o
u
b
l
e
double
double,
e
m
i
n
=
1
,
e
m
a
x
=
2046
e_{min}=1,e_{max}=2046
emin=1,emax=2046
E
∈
[
−
1022
,
1023
]
E\in[-1022,1023]
E∈[−1022,1023]

M
=
1
+
f
M=1+f
M=1+f
因为这里的
M
M
M 取值可以通过调整,使得
E
E
E 的取值使得总是有
M
∈
[
1
,
2
)
M\in[1,2)
M∈[1,2),所以这个
1
1
1 就可以省略,但是在计算时需要加上这个
1
1
1。
非规格化的值(Denormalized Values)
-
s
=
0
,
M
=
0
,
f
=
0
:
V
=
+
0.0
s=0, M=0,f=0: V=+0.0
s=0,M=0,f=0:V=+0.0
-
s
=
1
,
M
=
0
,
f
=
0
:
V
=
−
0.0
s=1, M=0,f=0: V=-0.0
s=1,M=0,f=0:V=−0.0
根据
I
E
E
E
IEEE
IEEE 的规则,
+
0.0
+0.0
+0.0 和
−
0.0
-0.0
−0.0 在某些方面是不同的,在大部分方面是相同的
非规格化的值另外一个用途是可以表示非常接近
0
0
0 的数
当阶码字段全为
0
0
0 时,阶码
E
=
1
−
b
i
a
s
,
M
=
f
E=1-bias,M=f
E=1−bias,M=f。注意这里是非规格化的值,不要用规格化的值的方式去解释非规格化的值 。
特殊值(Special Values)
当阶码字段二进制位全为
1
1
1,是无穷大
当
s
=
0
,
f
=
0
:
V
=
+
∞
s=0,f=0: V=+∞
s=0,f=0:V=+∞
当
s
=
1
,
f
=
0
:
V
=
−
∞
s=1,f=0: V=-∞
s=1,f=0:V=−∞
当
f
≠
0
:
V
=
N
a
N
f\neq 0: V=NaN
f=0:V=NaN
当运算结果不为实数,或者用无穷也无法表示的情况,这些均为
N
a
N
(
N
o
t
a
N
u
m
b
e
r
)
NaN(Not\ a\ Number)
NaN(Not a Number)
如下是一个
8
8
8 位的浮点数
符号位
s
s
s
e
x
p
exp
exp 是
4
4
4 位,
b
i
a
s
=
2
4
−
1
−
1
=
7
bias=2^{4-1}-1=7
bias=24−1−1=7
f
r
a
c
frac
frac 是
3
3
3 位
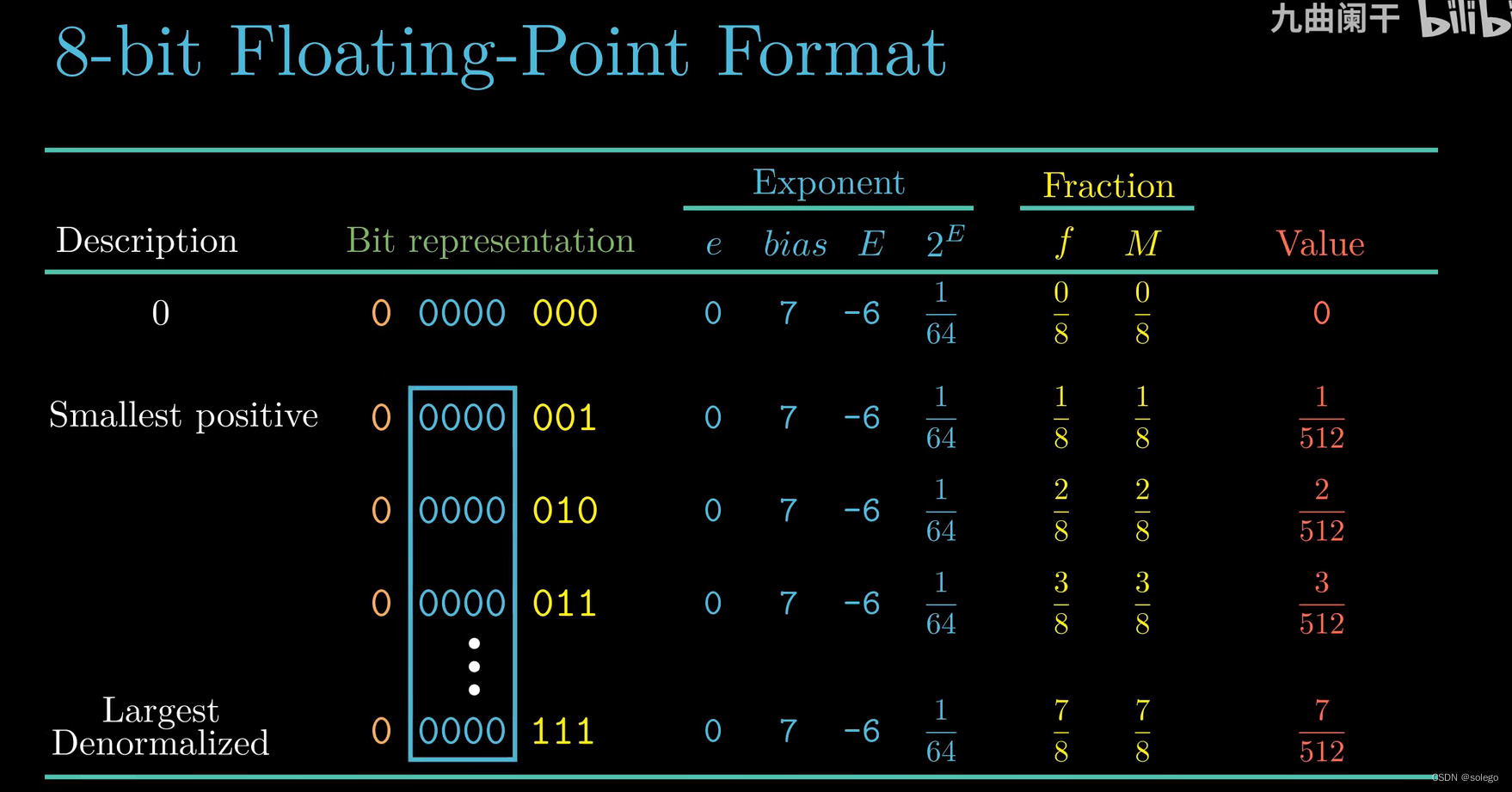
V
=
(
−
1
)
s
×
M
×
2
E
V = (-1)^s\times M \times 2^{E}
V=(−1)s×M×2E
舍入操作
对于一个浮点数,如果将其舍入为正数,该如何舍入呢?
对于
1.5
1.5
1.5 ,将其舍入为整数,应该舍入成
1
1
1 还是
2
2
2 呢?
舍入操作分为
4
4
4 种:
- 向下舍入
(
R
o
u
n
d
−
d
o
w
n
)
(Round-down)
(Round−down):朝向数值小的方向舍入
- 向上舍入
(
R
o
u
n
d
−
u
p
)
(Round-up)
(Round−up):朝向数值大的方向舍入
- 向零舍入
(
R
o
u
n
d
−
t
o
w
a
r
d
s
−
z
e
r
o
)
(Round-towards-zero)
(Round−towards−zero):朝向零的方向舍入
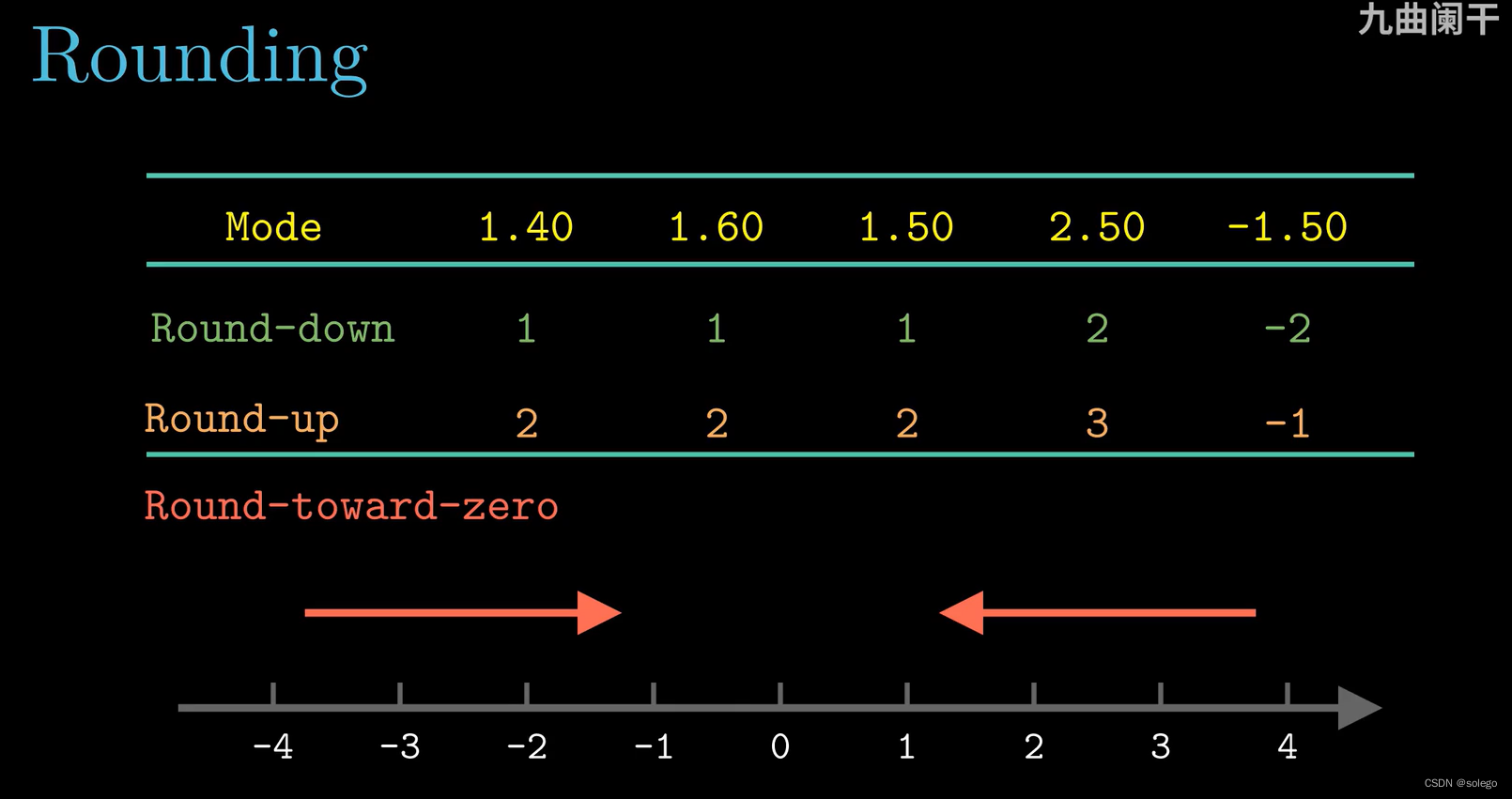
- 向偶数舍入
(
R
o
u
n
d
−
t
o
−
e
v
e
n
)
(Round-to-even)
(Round−to−even):向最近的值舍入,小数点
4
4
4 舍
6
6
6 入,如果为
5
5
5,则向偶数舍入,如
1.5
1.5
1.5 向
2
2
2 舍入,
2.5
2.5
2.5 也向
2
2
2 舍入。

浮点数的运算

(1)和(2)说明浮点数加法不满足结合律
(3)和(4)说明浮点数乘法不满足结合律
(5)和(6)说明浮点数乘法不满足分配律
类型转换
-
int -> float,由于 float的小数字段是
23
23
23 位,int 是
32
32
32 位数,所以可能会导致精度丢失
-
int/float -> double,由于 double 小数字段是
52
52
52 位,因此可以保留精确的数值
此外,float -> double 时,float精度相较于 double 较小,转换后可能被舍入
-
double -> float 可能会溢出
-
float/double -> int 一种可能的是向零舍入,另一种可能的是发生溢出