目录
1.用来做什么?
2.线性卡尔曼滤波
3.扩展卡尔曼滤波
4.无迹卡尔曼滤波
1.用来做什么?
——针对系统的不确定性:1.不存在完美的数学模型
2.系统的扰动不可控、也很难建模
3.测量传感器存在误差
例1:通过系统的状态方程得出的电流值i1,和传感器测得的电流值i2,由于不确定性的存在,两个值都不准确,所以i1和i2通过卡尔曼滤波算法算出其最接近真实值的值。
例2:如小红同学说今天老师穿的是红色的衣服(根据以往经验,每周四老师都穿红衣服,小红得出的结论),小白说老师今天穿的白色的衣服(看到一个像老师的人穿的白色的衣服,小白得出老师穿白色衣服的结论),通过卡尔曼滤波推算谁说话的权重更大,则推断出更应该相信谁的话。
2.线性卡尔曼滤波
系统真实方程为(状态方程的基础上存在噪声):


先验估计(他叫这名):
 —— 这是系统状态方程(方程建立的不准确性)
—— 这是系统状态方程(方程建立的不准确性)
 —— 这是先验误差协方差(用来算卡尔曼增益)
—— 这是先验误差协方差(用来算卡尔曼增益)
——(注意:噪声满足 ,其中0是期望值,
,其中0是期望值,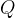 是协方差矩阵。
是协方差矩阵。 这里是
这里是 误差的期望/协方差(越接近0越好)。
误差的期望/协方差(越接近0越好)。
![P_{k}^{-}=E[e^{-}_{k}*e^{-}_{k}{T}] =AE[e_{k-1}e_{k-1}^{T}]A^{T}+E[w_{k-1}w_{k-1}^{T}] =AP_{k-1}A^{T}+Q](https://latex.csdn.net/eq?P_%7Bk%7D%5E%7B-%7D%3DE%5Be%5E%7B-%7D_%7Bk%7D*e%5E%7B-%7D_%7Bk%7D%7BT%7D%5D%20%3DAE%5Be_%7Bk-1%7De_%7Bk-1%7D%5E%7BT%7D%5DA%5E%7BT%7D+E%5Bw_%7Bk-1%7Dw_%7Bk-1%7D%5E%7BT%7D%5D%20%3DAP_%7Bk-1%7DA%5E%7BT%7D+Q)
后验估计(所要求的值):
因为: ——(传感器测量的不准确性)
——(传感器测量的不准确性)



 ——后验得到的值
——后验得到的值
![P_{k}=E[e_{k}*e_{k}^{T}]](https://latex.csdn.net/eq?P_%7Bk%7D%3DE%5Be_%7Bk%7D*e_%7Bk%7D%5E%7BT%7D%5D) ——
—— (真实值与后验估计误差的期望(目标期望为0))
(真实值与后验估计误差的期望(目标期望为0))
![=E[(x_{k}-\widehat{x}_{k})(x_{k}-\widehat{x}_{k})^{T}]](https://latex.csdn.net/eq?%3DE%5B%28x_%7Bk%7D-%5Cwidehat%7Bx%7D_%7Bk%7D%29%28x_%7Bk%7D-%5Cwidehat%7Bx%7D_%7Bk%7D%29%5E%7BT%7D%5D)
其目标为P的期望为0或方差最小(使后验估计与真实值误差最小),通过推导可以得到卡尔曼增益:
 ——(
——(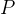 最小时求得的
最小时求得的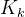 )
)
同时可以得到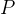 :
:
 —— (用来更新
—— (用来更新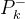 值)
值)
3.扩展卡尔曼滤波
卡尔曼滤波主要用于分析线性系统。
扩展卡尔曼滤波主要用于分析非线性系统。(正态分布的随机变量通过非线性系统后就不再是正态的了) 。
扩展卡尔曼滤波——主要是通过泰勒级数一阶展开,将非线性系统线性化,之后的求取与线性化卡尔曼滤波一致。
非线性系统:




泰勒级数一阶展开式:

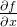 多维用雅克比矩阵
多维用雅克比矩阵
对非线性系统线性化。系统有误差,无法在真实点线性化,则 在
在 处线性化(
处线性化( 为
为 时的后验估计)
时的后验估计)

 等于0(误差假设为0)
等于0(误差假设为0) 雅克比矩阵
雅克比矩阵 雅克比矩阵。
雅克比矩阵。
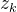 在
在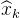 线性化:
线性化:

 ,
, 。
。
令 ,
, 。
。
 ——线性化后的系统方程
——线性化后的系统方程
先验估计:


后验估计:



标红部分为扩展和线性卡尔曼滤波的不同之处。
4.无迹卡尔曼滤波
由于扩展卡尔曼滤波可能存在线性化误差,且一般情况下雅克比矩阵不易实现,增加了算法的计算复杂度。
无迹卡尔曼滤波不采用泰勒展开实现非线性系统线性化,而是采用无迹变换(Unscented Transform,UT)来处理均值和协方差的非线性传递问题。(UKF算法是对非线性函数的概率密度分布进行近似,用一系列确定样本来逼近状态的后验概率密度,而不是对非线性函数进行近似,不需要对雅克比矩阵进行求导。)
无迹变换:
——(1)原状态分布中按某一规则选取一些采样点(其均值和方差等于原状态分布的均值和方差)
—— (2)将点带入非线性方程中(求取变换后的均值和协方差)
以对称分布采样的UT变换为例。设一个非线性变换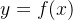 。状态向量
。状态向量 为
为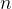 维随机变量,已知其均值
维随机变量,已知其均值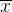 和方差
和方差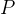 。通过UT变换得到2n+1个sigma点和相应的权值
。通过UT变换得到2n+1个sigma点和相应的权值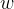 。
。
(1)计算2n+1个sigma点,即采样点

 表示矩阵方根的第
表示矩阵方根的第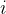 列。注意应确保
列。注意应确保 为半正定矩阵。
为半正定矩阵。
设:
 ,
,
则:
 ,
,  ——
—— 与
与 对称
对称
合并起来就是9个sigma点:
sig1 sig2 sig3 sig4 sig5 sig6 sig7 sig8 sig9

(2)计算采样点相应的权值

将9个sigma点带入非线性方程得到新的sigma点:

假设得到 sig1 sig2 sig3 sig4 sig5 sig6 sig7 sig8 sig9
 ,
,
定义权值 ,
,
可求得下一个点的先验值(经过UT变换后得到的先验值)


 (随便填的值,我就不算了哈哈哈)
(随便填的值,我就不算了哈哈哈)
以上是无迹变换算先验值的整个过程。
无迹卡尔曼滤波算法:
非线性系统:

步骤:
————1、经过UT变换求得sigma采样点及其权值

————2、计算2n+1个sigma点集的一步预测
![X^{^{(i)}}(k+1/k)=f[k,X^{i}(k/k)]](https://latex.csdn.net/eq?X%5E%7B%5E%7B%28i%29%7D%7D%28k+1/k%29%3Df%5Bk%2CX%5E%7Bi%7D%28k/k%29%5D)
————3、系统状态量的一步预测(相当于KF/EKF的先验值)
 ——UT变换后得到的新的状态值
——UT变换后得到的新的状态值
![P(k+1/k)=\sum_{i=0}^{2n}w^{i}[\widehat{X}(k+1/k)-{X}^{i}(k+1/k)][\widehat{X}(k+1/k)-{X}^{i}(k+1/k)^{T}]+Q](https://latex.csdn.net/eq?P%28k+1/k%29%3D%5Csum_%7Bi%3D0%7D%5E%7B2n%7Dw%5E%7Bi%7D%5B%5Cwidehat%7BX%7D%28k+1/k%29-%7BX%7D%5E%7Bi%7D%28k+1/k%29%5D%5B%5Cwidehat%7BX%7D%28k+1/k%29-%7BX%7D%5E%7Bi%7D%28k+1/k%29%5E%7BT%7D%5D+Q)
————4、再次使用UT变换,产生新的sigma点集

————5、新的sigma点集带入观测方程,得到预测的观测量
![Z^{i}(k+1/k)=h[X^{i}(k+1/k)]](https://latex.csdn.net/eq?Z%5E%7Bi%7D%28k+1/k%29%3Dh%5BX%5E%7Bi%7D%28k+1/k%29%5D)
————6、通过加权求得观测量新的均值及协方差
 ——UT变换后得到的新的观测值
——UT变换后得到的新的观测值
![Pz_{k}z_{k}=\sum_{i=0}^{2n}w^{i}[Z^{i}(k+1/k)]-\overline{Z}(k+1/k)][Z^{i}(k+1/k)]-\overline{Z}(k+1/k)]^{T}+R](https://latex.csdn.net/eq?Pz_%7Bk%7Dz_%7Bk%7D%3D%5Csum_%7Bi%3D0%7D%5E%7B2n%7Dw%5E%7Bi%7D%5BZ%5E%7Bi%7D%28k+1/k%29%5D-%5Coverline%7BZ%7D%28k+1/k%29%5D%5BZ%5E%7Bi%7D%28k+1/k%29%5D-%5Coverline%7BZ%7D%28k+1/k%29%5D%5E%7BT%7D+R)
![Px_{k}z_{k}=\sum_{i=0}^{2n}w^{i}[X^{i}(k+1/k)]-\overline{X}(k+1/k)][Z^{i}(k+1/k)]-\overline{Z}(k+1/k)]^{T}](https://latex.csdn.net/eq?Px_%7Bk%7Dz_%7Bk%7D%3D%5Csum_%7Bi%3D0%7D%5E%7B2n%7Dw%5E%7Bi%7D%5BX%5E%7Bi%7D%28k+1/k%29%5D-%5Coverline%7BX%7D%28k+1/k%29%5D%5BZ%5E%7Bi%7D%28k+1/k%29%5D-%5Coverline%7BZ%7D%28k+1/k%29%5D%5E%7BT%7D)
————7、 计算卡尔曼增益

————8、系统的状态更新和协方差更新
![\widehat{X}(k+1/k+1)=\widehat{X}(k+1/k)+K(k+1)[Z(k+1)-\widehat{Z}(k+1/k)]](https://latex.csdn.net/eq?%5Cwidehat%7BX%7D%28k+1/k+1%29%3D%5Cwidehat%7BX%7D%28k+1/k%29+K%28k+1%29%5BZ%28k+1%29-%5Cwidehat%7BZ%7D%28k+1/k%29%5D)


图1. 卡尔曼滤波流程图
实际应用(仿真分析):
系统方程:


 ,
, ,
,![Q=\sigma _{w}*diag([1,1])](https://latex.csdn.net/eq?Q%3D%5Csigma%20_%7Bw%7D*diag%28%5B1%2C1%5D%29) ,
, 。
。
真实状态信息为:
![X_{real}(k)=[x_{real}(k),\dot{x}_{real}(k),y_{real}(k),\dot{y}_{real}(k)]^{T}](https://latex.csdn.net/eq?X_%7Breal%7D%28k%29%3D%5Bx_%7Breal%7D%28k%29%2C%5Cdot%7Bx%7D_%7Breal%7D%28k%29%2Cy_%7Breal%7D%28k%29%2C%5Cdot%7By%7D_%7Breal%7D%28k%29%5D%5E%7BT%7D)
UKF滤波算法得到的目标状态为:
![X_{UKF}(k)=[x_{UKF}(k),\dot{x}_{{UKF}}(k),y_{{UKF}}(k),\dot{y}_{{UKF}}(k)]^{T}](https://latex.csdn.net/eq?X_%7BUKF%7D%28k%29%3D%5Bx_%7BUKF%7D%28k%29%2C%5Cdot%7Bx%7D_%7B%7BUKF%7D%7D%28k%29%2Cy_%7B%7BUKF%7D%7D%28k%29%2C%5Cdot%7By%7D_%7B%7BUKF%7D%7D%28k%29%5D%5E%7BT%7D)
定义均方根误差(RMSE):


代码:
T=1;
N=60/T;
X=zeros(4,N); ——定义X为4行60列的数列
X(:,1)=[-100,2,200,20]; ——第一个点
Z=zeros(1,N); ——定义Z为1行60列的数列
delta_w=1e-3;
Q=delta_w*diag([0.5,1]); ——状态噪声
G=[T^2/2,0;T,0;0,T^2/2;0,T];
R=5; ——观测噪声
F=[1,T,0,0;0,1,0,0;0,0,1,T;0,0,0,1];
x0=200;
y0=300; ——可以随便给定(Z方程里的值)
Xstation=[x0,y0];
v=sqrtm(R)*randn(1,N);
for t=2:N
X(:,t)=F*X(:,t-1)+G*sqrtm(Q)*randn(2,1);
end
for t=1:N
Z(t)=Dist(X(:,t),Xstation)+v(t);
end ——真实状态值和观测值


L=4;
alpha=1;
kalpha=0;
belta=2;
ramda=3-L;
for j=1:2*L+1
Wm(j)=1/(2*(L+ramda));
Wc(j)=1/(2*(L+ramda));
end
Wm(1)=ramda/(L+ramda); ——求第一次方差的权值
Wc(1)=ramda/(L+ramda)+1-alpha^2+belta; ——求第一次均值的权值
Wm
Wc

Xukf=zeros(4,N);
Xukf(:,1)=X(:,1);
P0=eye(4);
for t=2:N ——(注:下面给出的数据是第一次循环)
xestimate=Xukf(:,t-1);
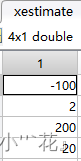
P=P0; ——初始协方差随便给定 (4行4列矩阵)
cho=(chol(P*(L+ramda)))'; ——半正定矩阵
for k=1:L
xgamaP1(:,k)=xestimate+cho(:,k);

xgamaP2(:,k)=xestimate-cho(:,k); —— xgamaP1的1列与xgamaP2的1列关于xestimate对称
xgamaP1的2列与xgamaP2的2列对称
xgamaP1的3列与xgamaP2的3列对称
xgamaP1的4列与xgamaP2的4列对称
end
Xsigma=[xestimate,xgamaP1,xgamaP2]; ——求出第一步的9个sigma点

Xsigmapre=F*Xsigma; ——9个sigma点带入非线性函数得到新的9个sigma点

Xpred=zeros(4,1);
for k=1:2*L+1
Xpred=Xpred+Wm(k)*Xsigmapre(:,k); ——新的状态值(先验值)4行1列
end

Ppred=zeros(4,4);
for k=1:2*L+1
Ppred=Ppred+Wc(k)*(Xsigmapre(:,k)-Xpred)*(Xsigmapre(:,k)-Xpred)';
end
Ppred=Ppred+G*Q*G'; ——新的协方差

chor=(chol((L+ramda)*Ppred))';
for k=1:L
XaugsigmaP1(:,k)=Xpred+chor(:,k);
XaugsigmaP2(:,k)=Xpred-chor(:,k);
end
Xaugsigma=[Xpred XaugsigmaP1 XaugsigmaP2]; ——先验值经UT变化得到新的9个sigma点 (用来算Z值)

for k=1:2*L+1;
Zsigmapre(1,k)=hfun(Xaugsigma(:,k),Xstation);——9个sigma点带入非线性函数得到新的9个 end sigma点,公式
 Zpred=0;
Zpred=0;
for k=1:2*L+1
Zpred=Zpred+Wm(k)*Zsigmapre(1,k); ——新的Z值
end
Pzz=0;
for k=1:2*L+1
Pzz=Pzz+Wc(k)*(Zsigmapre(1,k)-Zpred)*(Zsigmapre(1,k)-Zpred)'; ——用来求卡尔曼增益
end
Pzz=Pzz+R;

Pxz=zeros(4,1);
for k=1:2*L+1
Pxz=Pxz+Wc(k)*(Xaugsigma(:,k)-Xpred)*(Zsigmapre(1,k)-Zpred)'; ——用来求卡尔曼增益
end

K=Pxz*inv(Pzz);

xestimate=Xpred+K*(Z(t)-Zpred); ——最终求得的值

P=Ppred-K*Pzz*K'; ——更新协方差值
P0=P;
Xukf(:,t)=xestimate; ——迭代
end
for i=1:N
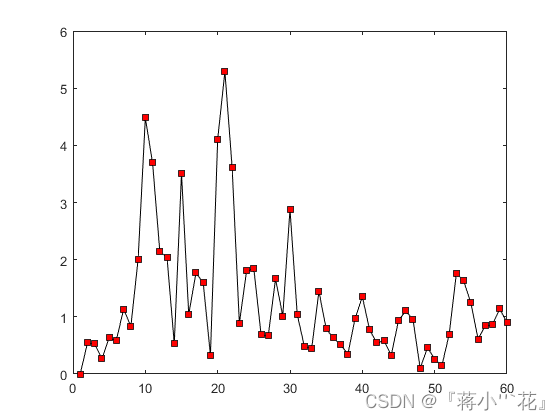
Err_KalmanFilter(i)=Dist(X(:,i),Xukf(:,i));
end
figure
hold on;box on;
plot(X(1,:),X(3,:),'-k.');
plot(Xukf(1,:),Xukf(3,:),'-r+');
legend('真实轨迹','UKF轨迹')
figure
hold on;box on;
plot(Err_KalmanFilter,'-ks','MarkerFace','r')
调用函数1:
function d=Dist(X1,X2)
if length(X2)<=2
d=sqrt((X1(1)-X2(1))^2+(X1(3)-X2(2))^2);
else
d=sqrt((X1(1)-X2(1))^2+(X1(3)-X2(3))^2);
end
调用函数2:
function[y]=hfun(x,xx)
y=sqrt((x(1)-xx(1))^2+(x(3)-xx(2))^2);
参考视频:
【卡尔曼滤波器】1_递归算法_Recursive Processing_哔哩哔哩_bilibili
参考书本:
卡尔曼滤波原理及应用——MATLAB仿真