概述
在上一篇文章中讲述了Kruskal和Prim算法，用于得到最小生成树，今天将会介绍两种得到最短路径的算法——Dijlkstra和Bellman-Ford算法
Dijkstra算法
上面的特点在我讲完这个算法的思想之后你就会明白为什么了。
算法思想：
这个算法的思想其实特别贴近生活，如果你把每个点都想象成一个小石头，每个边都想成一根绳子，边的权值表示绳长。然后，我们选择其中一个石头，作为第一个从地上被拉起来的，将其慢慢地从地上拿起来，之后肯定会有一个离它最近的小石头也会被拉起来，就这样不断往上提，最终所有石头都会被提起来。好了，说完了这个例子后，我想问你一个比较常识性的问题：除了第一块石头外，每块被拉起来的石头是否都是被前一个被拉起来的石头所拉起来的？当你相通了这个，后面当我解释过程的时候就好说了
我们先来看一下下面这个例子：我们以A为起点，按照我们之前的例子去挨个提起来:
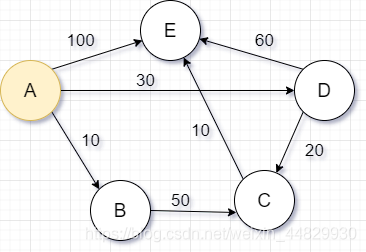
过程：
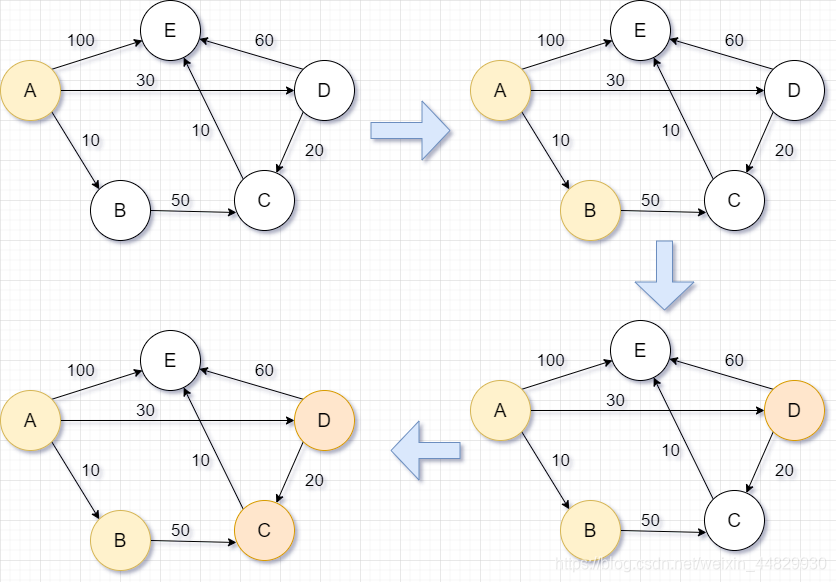
上面是使用该算法的一个过程图，我们现在来对其进行一个解释，并且，为了方便记录最短路径，我会用一个表来记录最短路径
以A为源点，并且将A点所直接指向的顶点的路径信息记录到该表中。从图中不难看出提起来的第一块石头是B，它是被A提起来的，因此更新A到B的最短路径信息，我们发现和原来是一样的
| 终点 | 最短路径 | 长度 |
|---|---|---|
| B | A -> B | 10 |
| C | ∞ | |
| D | A -> D | 30 |
| E | A -> E | 100 |
接下来，下一个被踢起来的是D，它是被A提起来的，更新其最短路径，更新后的路径信息也是和原来一样
| 终点 | 最短路径 | 长度 |
|---|---|---|
| B | A -> B | 10 |
| C | ∞ | |
| D | A -> D | 30 |
| E | A -> E | 100 |
很明显，下一个被踢起来的是C，它是被谁提起来的呢？看一下图就知道，它是被D所提起来的。为什么我总是强调是被谁提起来的这个问题呢？还记得我之前在说思想的时候说过的问题吗？正是因为每个被提起来的石头都是被上一个已经被提起的石头所提起来的，所以他的最短路径就是，提起他的那块石头的最短路径再到达当前被提起的石头的最短路径就是当前石头的最短路径了。
如果听着有点蒙，我们用这一步的这个例子给你说明一下，当前C被D所提起来，因此A到C的最短路径就是A到D的最短路径加上D到C的最短路径，权值也是在上一条路径的基础上进行相加得到的。我们发现此时的路径信息50要小于一开始的路径长度∞，因此更新后最短路径信息就变成了下面这样了
| 终点 | 最短路径 | 长度 |
|---|---|---|
| B | A -> B | 10 |
| C | A -> D -> C | 50 |
| D | A -> D | 30 |
| E | A -> E | 100 |
再往后就是最后一步了，E点被提起，它是被C所提起来的，并且此时的最短路径长度比表中的原来的路径长度要短，因此进行更新
| 终点 | 最短路径 | 长度 |
|---|---|---|
| B | A -> B | 10 |
| C | A -> D -> C | 50 |
| D | A -> D | 30 |
| E | A -> D -> C -> E | 60 |
至此，就得到了以A为起点到达其他点的最短路径信息了
参考代码（部分）
-
/**
* Dijkstra算法，原理：每个节点当做石头，每个边当做绳子，然后把往上拉
*
* 限制条件：图中不能有负权边，不然可能会出现，某个点被提起来之后，又发现了可以到达它的更短的边
* 也可以理解为，在选起点后，就存在某条权值为负数的路径，就是说已经被提起来了
*
* @return V - PathInfo
* PathInfo中存的是List<EdgeInfo<V, E> 和 weight
*/
@Override
public Map<V, PathInfo<V, E>> dijkstra(V begin) {
// 拿到起点
Vertex<V, E> beginVertex = vertices.get(begin);
if (Objects.isNull(beginVertex)) {
return null;
}
// 返回结果
Map<V, PathInfo<V, E>> result = new HashMap<>();
// 未拿起来的顶点
Map<Vertex<V, E>, PathInfo<V, E>> paths = new HashMap<>();
// 初始化paths里面一开始只有A->A weight=0这样一条路劲，然后进入下面的循环进行松弛
paths.put(beginVertex, new PathInfo<>(weightManager.zero()));
while (!paths.isEmpty()) {
// 选择一个最短路径所到达的顶点
Map.Entry<Vertex<V, E>, PathInfo<V, E>> minEntry = getMinPath(paths);
// 松弛操作
// 拿到顶点，即一块“石头”被提起
Vertex<V, E> minVertex = minEntry.getKey();
// 拿到当前最短边的PathInfo
PathInfo<V, E> minPathInfo = minEntry.getValue();
// 加入到result中
result.put(minVertex.value, minEntry.getValue());
// 从paths中删除
paths.remove(minVertex);
// 遍历该顶点的outEdges并试着更新边的to，这里遍历不能用foreach，否则不能continue
for (Edge<V, E> edge : minVertex.outEdges) {
// 为了适用于无向图，也要判断to指向的顶点是否已经被“提起”过，避免重复遍历
// 如果是begin则跳过，不能加到result中，在此处判断或者在返回前将其删除
if (result.containsKey(edge.to.value)) {
continue;
}
relaxForDijkstra(edge, paths, minPathInfo);
}
}
// 将起点从结果中移除
result.remove(begin);
return result;
}
代码中注释部分的松弛操作指的是提石头并更新最短路径信息。
小结
回顾之前的算法特点，我们回答一下为什么不能有负权边这个问题，其实就利用这个算法的提石头思想就可以解释，提石头的时候绳子的长度不能肯定不能是负的，如果是负的，那该算法就解决不了了，因为
Bellman-Ford算法
算法特点
算法思想
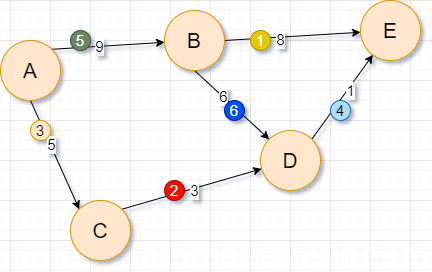
代码（部分）
public Map<V, PathInfo<V, E>> bellmanFord(V begin) {
// 拿到起点
Vertex<V, E> beginVertex = vertices.get(begin);
if (Objects.isNull(beginVertex)) {
return null;
}
// 初始化: 返回结果
Map<V, PathInfo<V, E>> result = new HashMap<>();
// 初始化起点，并放入result中
PathInfo<V, E> beginPathInfo = new PathInfo<>();
beginPathInfo.weight = weightManager.zero();
result.put(begin, beginPathInfo);
// 因为每次最少会找到一条，所以理论上最多循环V-1次就可以找到所有的
int count = vertices.size() - 1;
PathInfo<V, E> fromPathInfo;
for (int i = 0; i < count; i++) {
for (Edge<V, E> edge : edges) {
// 松弛操作，最开始这里可能为空，因此需要初始化起点并放入result
fromPathInfo = result.get(edge.from.value);
relax(edge, result, fromPathInfo);
}
}
// 再循环一次，判断是否有负权环，如果还有边可以进行松弛操作说明存在负权环
for (Edge<V, E> edge : edges) {
// 松弛操作，最开始这里可能为空，因此需要初始化起点并放入result
fromPathInfo = result.get(edge.from.value);
if (relax(edge, result, fromPathInfo)) {
System.out.println("存在负权环");
return null;
}
}
// 将起点从结果中移除
result.remove(begin);
return result;
}
解释： 该算法的原理就是按照一定的顺序将所有的路径不断的重复遍历，每次遍历都会通过搜对边进行松弛操作来发现最少一条最短路径，直到某次循环没有再发现新的最短路径的时候，这个时候说明最短路径已经都找到了，次时算法结束。也许你会对这个结束的条件有点疑惑，我们可以举个例子，假如某次循环更新了一条最短路径，那么是不是有可能该路径后面的路径也会发生变化呢？是不是要再次去遍历？当然要！
和上面的Dijkstra算法相似的是，都会维护一个数据结构用于保存最短路径信息，并且都是不断地去遍历路径。不一样的是遍历的方式有所不同，对于前者，每次找确定的边的时候都是找最短的那一条，确定了的边下次不会再去循环。对于后者，就按照一定的顺序去进行松弛即可，实现起来相对较简单。
还有一个问题还没有说，就是Bellman-Ford算法是如何检测负权环的？我们不妨先假设，有负权环 会怎么样：首先，负权环因为环路的总权值是负的，所以每走一圈，路径长度就会减少，每次松弛都会减 少，因此每次循环都会伴随着至少一次以上的最短路径信息更新操作。之前我们也说了，每次循环至少会 找到一条最短路径，那么如果要找到所有的最短路径，那么遍历的次数一定是有限的！，但是有负权环的 情况下就回无限循环，所以我们可根据循环次数来判断是否存在负权环！
总结
我们不妨先假设，有负权环 会怎么样：首先，负权环因为环路的总权值是负的，所以每走一圈，路径长度就会减少，每次松弛都会减 少，因此每次循环都会伴随着至少一次以上的最短路径信息更新操作。之前我们也说了，每次循环至少会 找到一条最短路径，那么如果要找到所有的最短路径，那么遍历的次数一定是有限的！，但是有负权环的 情况下就回无限循环，所以我们可根据循环次数来判断是否存在负权环！**
总结
本次学习了Dijkstra算法和Bellman-Ford算法，两种算法各有各的特点，前者不能存在负权边，后者可以允许负权边，并且可以检测负权环。前者是提石头的思想，后者则是不断的去重复走，直至熟悉所有最短路径