自治的(时间齐次的)一阶微分方程
x
˙
=
ϕ
(
x
)
(
6.1
)
\dot{x}=\phi(x) (6.1)
x˙=ϕ(x)(6.1)
其中,
x
˙
\dot x
x˙表示
∂
x
/
∂
t
\partial x/ \partial t
∂x/∂t,
x
˙
\dot x
x˙为向量组
(
x
˙
1
,
x
˙
2
,
.
.
.
,
x
˙
k
)
(\dot x_1,\dot x_2,...,\dot x_k)
(x˙1,x˙2,...,x˙k),
ϕ
\phi
ϕ是开集X到
R
k
R^{k}
Rk的映射,
X
=
{
x
1
,
x
2
.
.
.
,
x
k
}
X=\{x_1,x_2...,x_k\}
X={x1,x2...,xk}指的是状态空间,
ϕ
(
x
)
\phi(x)
ϕ(x)被称为向量场,定义了状态空间X中每个点上流的方向和速度(由x_k可以计算出\phi(x_k),用矩阵X进行的映射即为向量场\phi),由(6.1)解微分方程面临如下几个问题:
里普菲茨连续性
若对任意
x
,
y
∈
C
,
C
⊂
X
,
∃
λ
x,y\in C ,C\subset X,\exists \lambda
x,y∈C,C⊂X,∃λ使得
∣
∣
ϕ
(
y
)
−
ϕ
(
x
)
∣
∣
⩽
∣
∣
y
−
x
∣
∣
||\phi(y)-\phi(x)||\leqslant ||y-x||
∣∣ϕ(y)−ϕ(x)∣∣⩽∣∣y−x∣∣,则称函数
ϕ
\phi
ϕ是里普菲茨连续的。
一阶偏导数连续 严格于 里普菲茨连续 严格于 连续
picard_lindelof定理(解的存在性与唯一性)
如果
X
⊂
R
k
X\subset R^k
X⊂Rk是一个开集,且向量场
ϕ
:
X
→
R
k
\phi:X \rightarrow R^k
ϕ:X→Rk是里普菲茨连续的,那么(6.1)通过每个状态
x
0
∈
X
x^0 \in X
x0∈X有唯一的解映射
ξ
(
⋅
,
x
0
)
:
T
→
X
\xi(·,x^0):T\rightarrow X
ξ(⋅,x0):T→X,而且,
ξ
(
t
,
x
0
)
\xi(t,x^0)
ξ(t,x0)在
t
∈
T
t\in T
t∈T和
x
0
∈
X
x^0\in X
x0∈X时是连续的。
通过picard_lindelof定理可知,在足够平滑的向量场(满足里普菲茨连续性条件下),(局部)解的存在性与唯一性(满足初始条件的解)可以得到保证
解的全局性
定义:方程组(6.1)通过某个初始状态
x
0
∈
X
x^0\in X
x0∈X的解是一个函数
ξ
(
⋅
,
x
0
)
:
T
→
X
\xi(·,x^0):T \rightarrow X
ξ(⋅,x0):T→X,使得
ξ
(
0
,
x
0
)
=
x
0
\xi(0,x^0)=x^0
ξ(0,x0)=x0(在t=0时,满足初始条件),且下式对所有T=R均成立,则称解是全局的。
d
d
t
ξ
(
t
,
x
0
)
=
ψ
[
ξ
(
t
,
x
0
)
]
\dfrac{d}{dt}\xi(t,x^0)=\psi[\xi(t,x^0)]
dtdξ(t,x0)=ψ[ξ(t,x0)]
微分方程解的特殊情况
-
非里普菲茨连续情况下,常微分方程有多个解
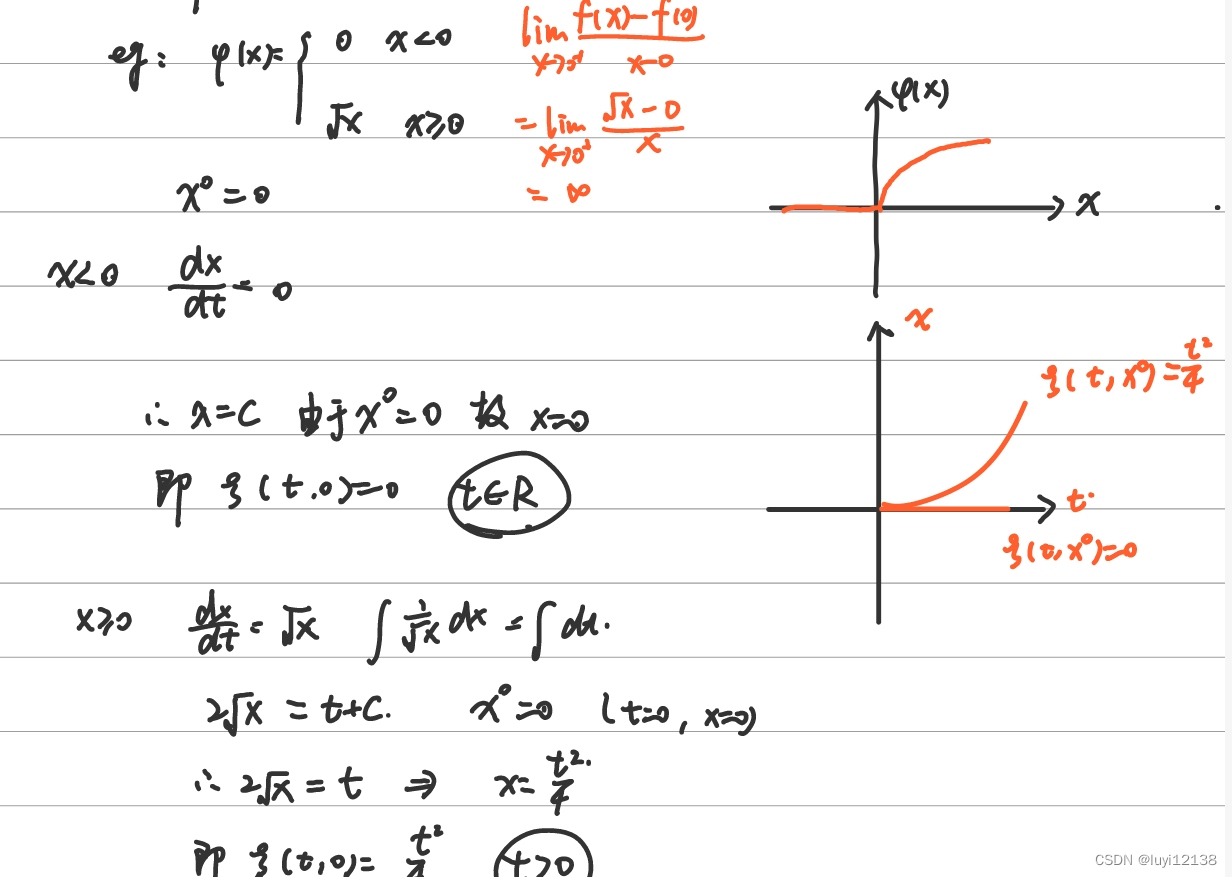
-
爆炸型解
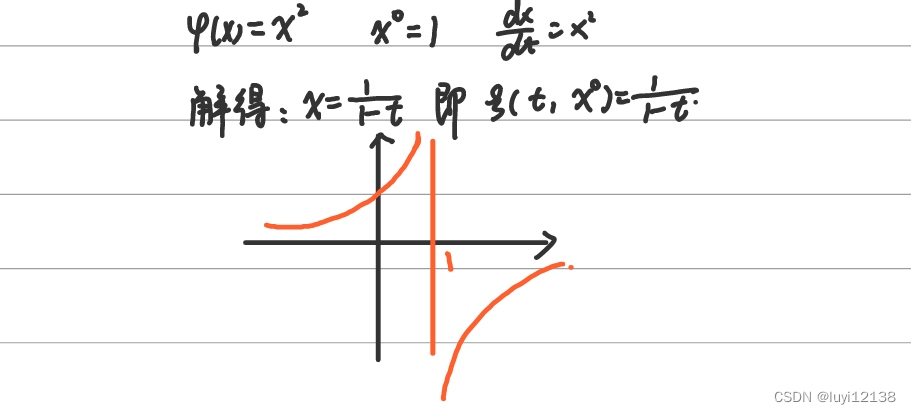
微分方程解法
例6.4
{
x
˙
1
=
ϕ
1
(
x
)
=
α
x
1
−
x
2
x
˙
2
=
ϕ
2
(
x
)
=
x
1
+
α
x
2
\begin{cases} \dot x_1=\phi_1(x)=\alpha x_1-x_2\\ \dot x_2=\phi_2(x)= x_1+\alpha x_2 \end{cases}
{x˙1=ϕ1(x)=αx1−x2x˙2=ϕ2(x)=x1+αx2

本文参考来源《演化博弈论》乔根·W·威布尔[著]