B站网课来自 3Blue1Brown的翻译版,看完醍醐灌顶,强烈推荐:
线性代数的本质
本课程从几何的角度翻译了线代中各种核心的概念及性质,对做题和练习效果有实质性的提高,下面博主来总结一下自己的理解
1.向量的本质
在物理中的理解是一个有起点和终点的方向矢量,而在计算机科学中的理解——更像是某种类似于列表的结构体(只不过这是一种以数字为元素的列表)。
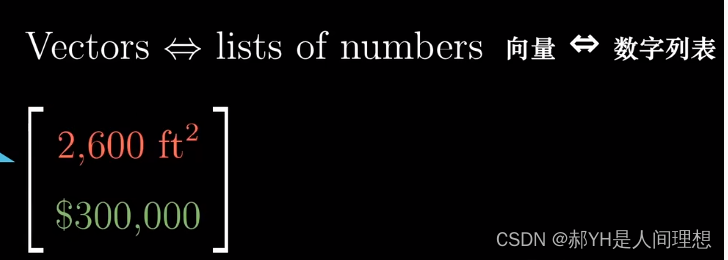
对应在数学的领域,可以理解为一种坐标——分别用列表中的项来对应起点与终点(二维向量)。
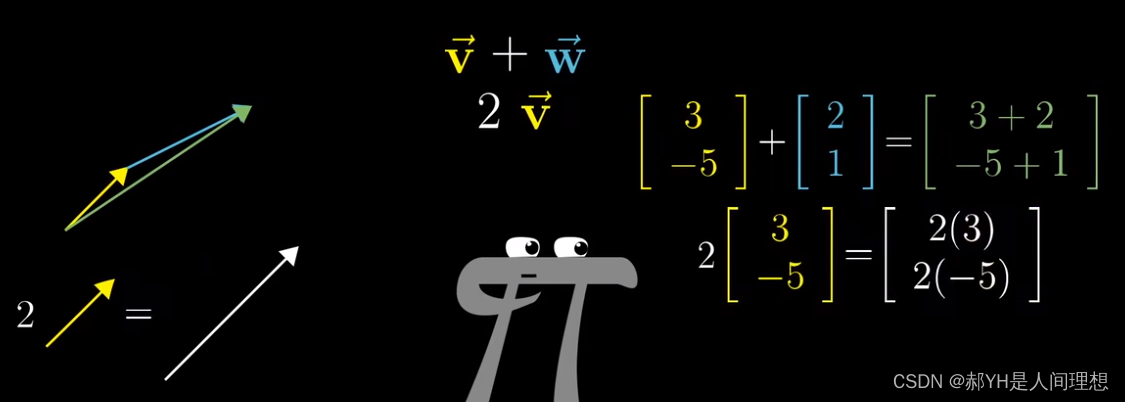
而向量加法的本质,即为对应维度上的线性相消。 而另一种理解为,向量是空间中的某种运动,在不同维度上的线性抵消,如下图——这一性质也可以扩展到n维。
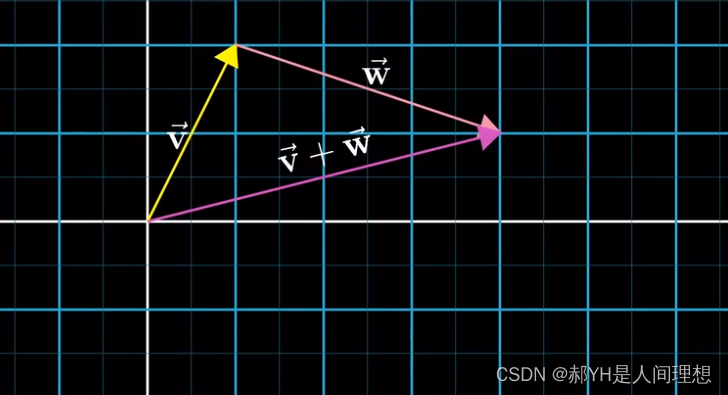
2.向量的坐标
首先理解单位向量的概念——i(1,0),j(0,1),由i与j的线性相加可以得到空间中的任一向量~
而向量【-3,2】,可以将两个元素理解为2个标量——即对向量的拉伸与压缩。
而基向量,也就是单位向量,即为所谓拉伸与压缩的对象!
两个数型向量的相加,被称为这2个向量的线性组合~
对于线性的一种理解:只允许1个标量变化,其余n-1个维度的坐标固定,所产生的向量集即为一条直线!
3.张成空间
定义:所有可以表示为给定向量线性组合的向量的集合。
- 对于二维,表示所有二维空间中向量的集合,亦或终点相同的向量的集合
- 对于三维,表示一个平面或者一个空间
4.线性相关与线性无关
- 所谓线性相关,即向量组中至少有一个是多余的,即没有对张成空间的形成做出贡献——换句话说,有至少一个向量可由其他向量线性相加获得(线性组合)
- 而所谓线性无关,即每一个向量的存在都会使得张成空间的维度增加
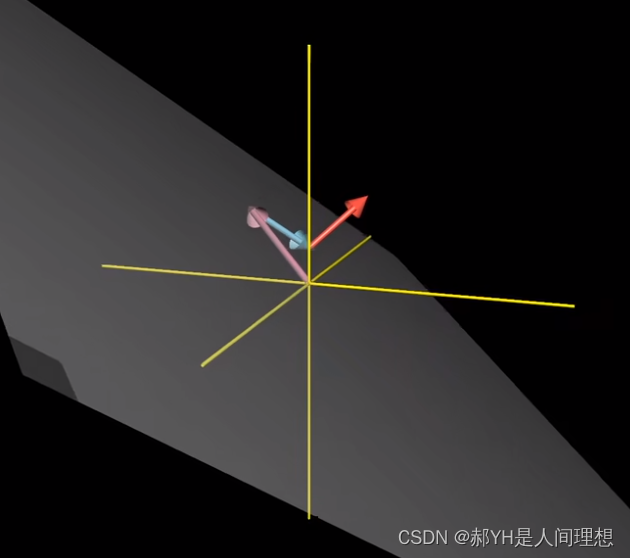
5.矩阵的本质——线性变换
所谓变化,其实就是函数的一种花哨说法~
本质上,向量a是由i和j的一个线性组合,而空间发生变化后a1则变为了同样发生变化的i1与j1与原来保持一致的线性组合!

所以,如果将变化后的i1与j1按照列向量合集表示,如下图,即形成了所谓的矩阵!
也就是说,在二维空间的线性变换,仅由4个数就可以决定!
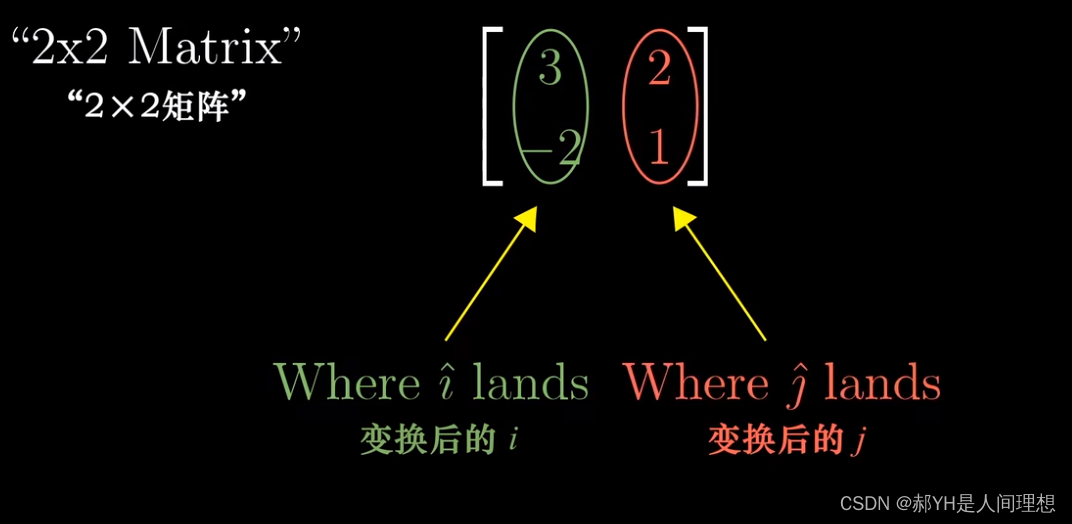 此刻若给出一个矩阵和一个已知变量 ,即可得出:对该向量进行目标矩阵的变换后可以得出的新向量!
此刻若给出一个矩阵和一个已知变量 ,即可得出:对该向量进行目标矩阵的变换后可以得出的新向量!
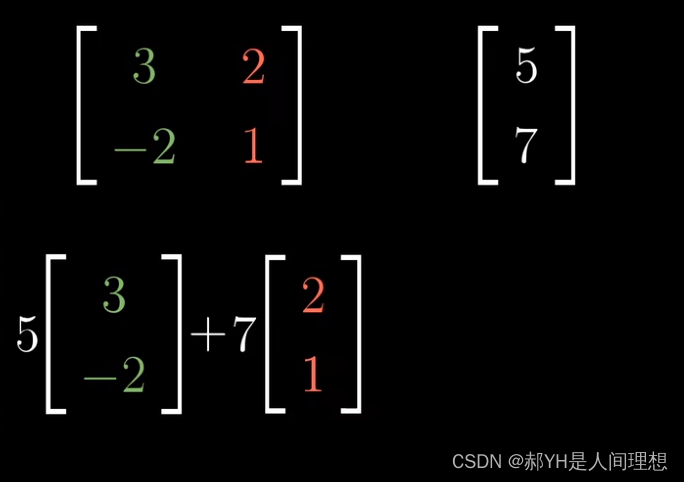
关于上面的一个理解,不要晕:所谓的5/7,本质上的意味是:a=5i+7j,也就是说,所谓的目标向量,本质也是对i和j的一种变化!!!而为什么有的变化就是向量,而有的变化就是矩阵呢?那是因为,所谓的5/7,他对应的均为当前方向上的变化——即翻倍延长,而矩阵中,第一行的变化,均为在i方向上的变化,而第二行则全部对应j方向的变化——也就是说,矩阵变化后的i1和j1,实际上是在两个方向上同时变化!!!因此不难理解矩阵乘法的底层逻辑:这里第一行乘以第一列的意义,实际上是原来对应的5i,在i变成i1后所需要对应的变化——即i方向变3,j方向变2!第二行也是同理~此刻即使扩展到n维,这一原理仍成立!
再进行一个更炸裂的理解:所谓m行n列的矩阵,m即为当前基向量的个数——即坐标系的维度,而所谓的mn列,即为对原始的基向量,需要进行几维的线性变换!
因此,我们可以说:矩阵的本质就是一种线性变换!(也就是作用于向量的函数)
6.矩阵的乘法
如果将矩阵理解为一种线性变换,那么矩阵的相乘本质即为连续的线性变换~

注意一个细节——同函数一致,需要向右往左看!
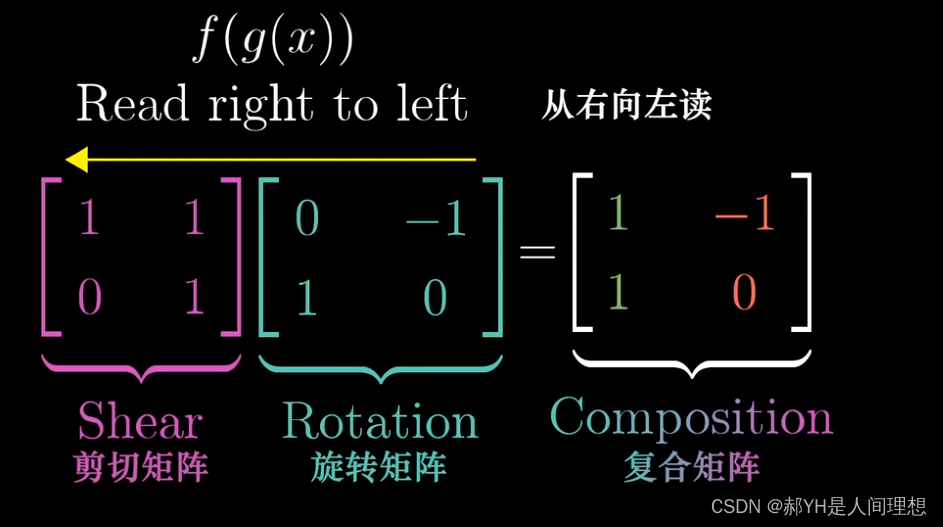
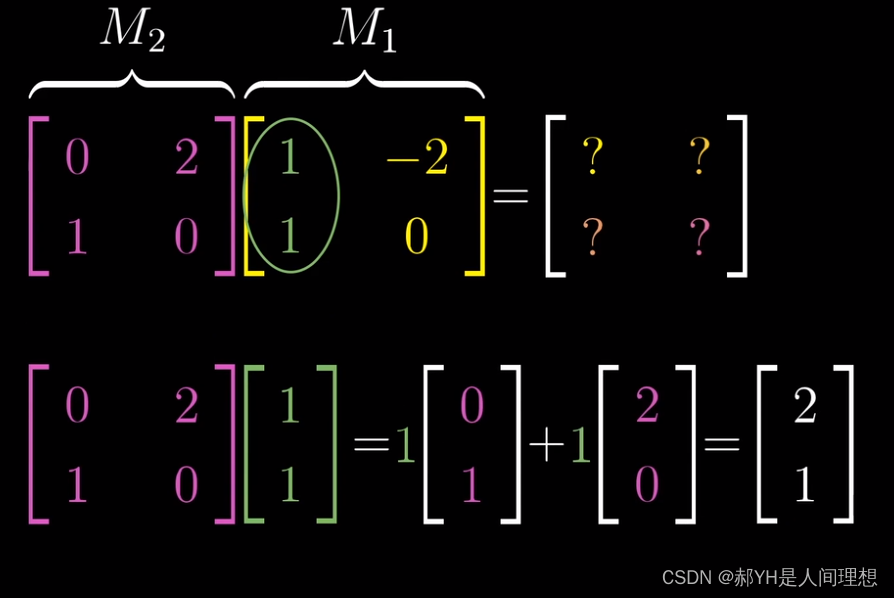
对于相乘后得到的矩阵:第一列即为第一个矩阵进行变换变为i1后,第二个矩阵使他变换为了i2;j2的诞生亦是如此~
至于乘法的规则,再描述一遍:如上的1/1,即为对i的变化,现在需要将i1变化为i2,则需要再对i1进行i和j两个维度上的一次变化! 所以i1的i方向1在i上变0,j上变1;j1的i方向上2而j方向上变0!
非常抽象,需要反复琢磨!
7.三维空间中的线性变换
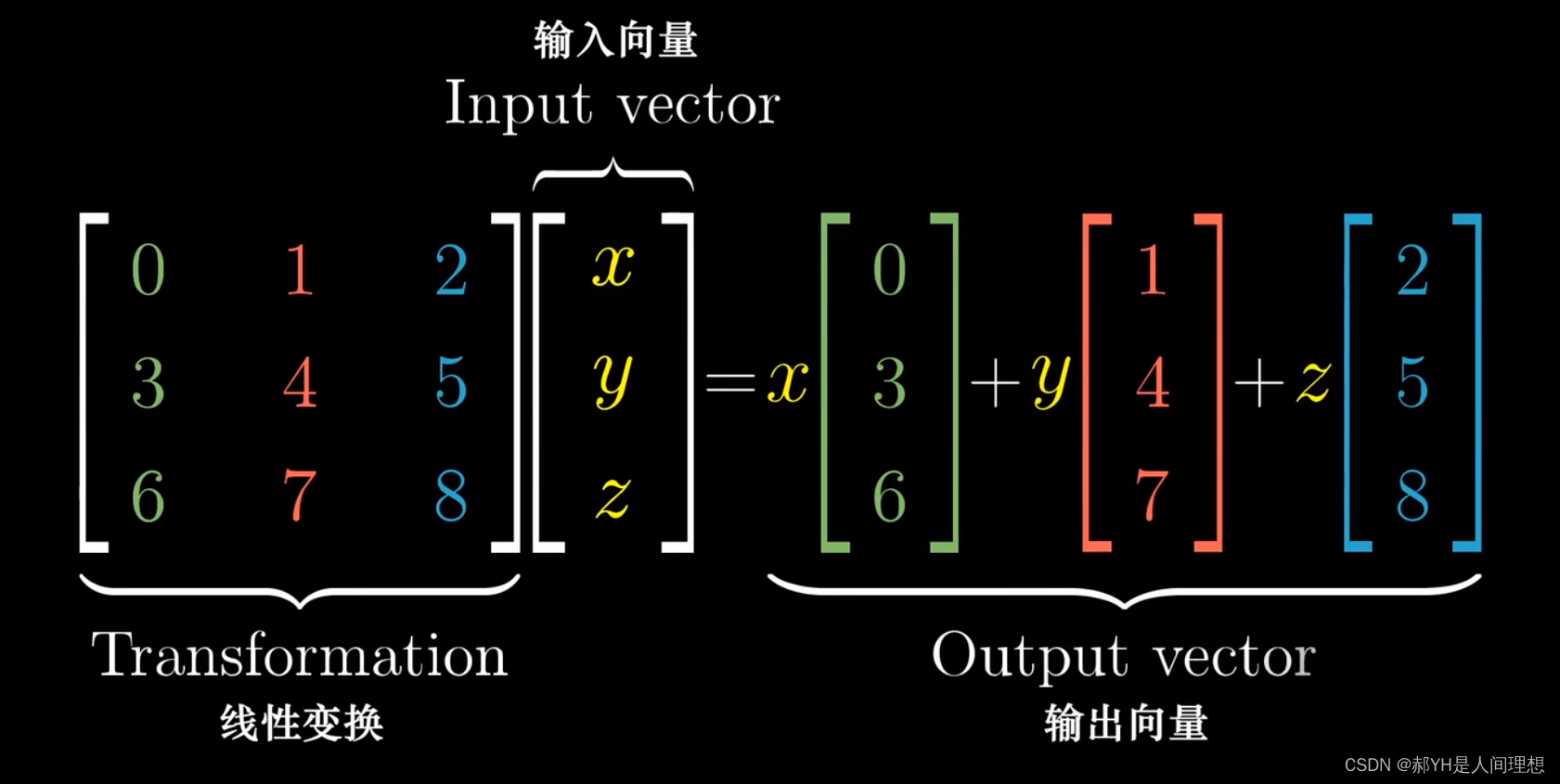
同二维平面一致,此处仅需要9个数,即可完成三维空间下的线性变换,将这9个数组为三维向量。
此处对3维方阵与向量的乘积做出如下两种理解:
- 首先,按列看,1~3列可以分别对应为基向量i、j、k的线性变换,而按行看,则代表i、j、k向量在当前所对应的维度上各自的变化量。
- 另一种解释,如上图,xyz后面的向量,实际意义是经过线性变换后坐标系里的基向量,而此刻把xyz可以理解为一种给定的标量,并作用于当前变换后的基向量
8.行列式
单位正方形:在二维平面内,以i和j两个基向量为边所圈成的正方形
行列式的本质,即为线性变换对原面积改变的比例——行列式的值即为对面积的缩放比例数值
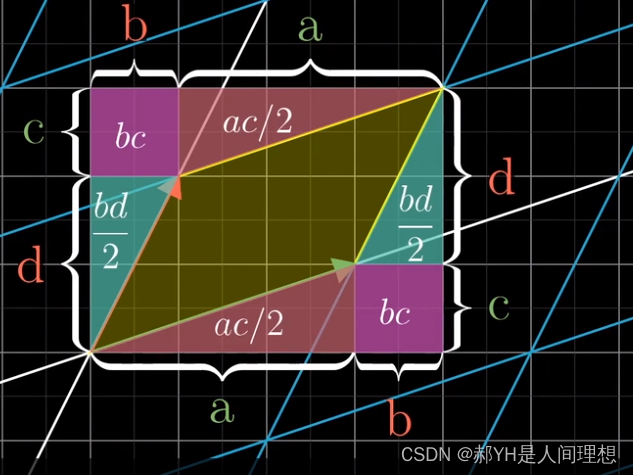
- 在二维平面里,如果行列式的值为负,本质是在将矩阵翻转~
- 在三维空间里,行雷士的值即为对应体积的缩放比例~
在三维的情况下,当行列式为0时,即当前的体积被压缩为0,几何角度的理解为:存在共线向量、共面甚至重合的一个点!——这便是所谓线性相关的几何意义。
这也从某种角度解释了——为什么对应的行列式为0的向量组必然线性相关,实质上还是那个理解,存在未对维度变化做出贡献的向量
(可以说,空间压缩的本质是行列式为0)
9.线性方程组
首先要注意——线性方程组存在的意义和向量的乘法非常的类似~
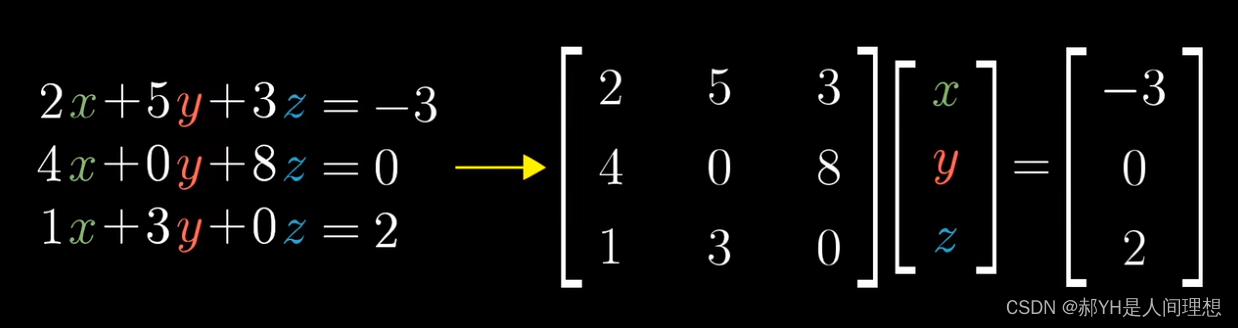
如上是一种非常具有技巧性的理解:方程组可以表示为矩阵与向量的积
其中系数矩阵A本质上就是对于向量的某种函数;而这里的向量是一个未知数,由x/y/z三个未知的数值表示。
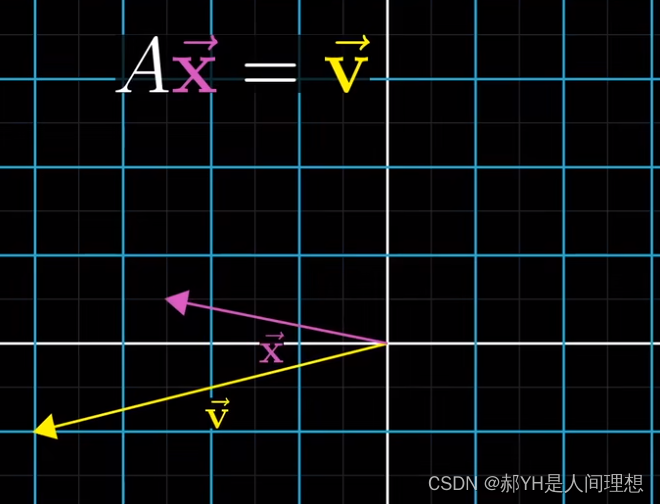
上述Ax=v的理解可以有两种:
- 矩阵代表一种线性变换,在一元函数中可以理解为k、b这样的常数,而xyz组成的向量本质上就是一元函数中的自变量
- 同理,依旧可以理解为,xyz是对当前经过矩阵A变换后的新的基向量的数值,则这一方程本质上变为了求解标量xyz的过程
10.逆矩阵
顾名思义,几何意义即为逆向的线性变换。
存在的意义为,A-1和A可以相互抵消,形成一个本质上什么都做的变换,这样的变换又被称为恒等变换
单位矩阵E的集合意义在这里就解释得同了:对角线为1的性质,带来了仅对当前向量的基向量所对应维度的变换,且倍数为1。
11.秩
本质为线性变换后的空间维数(国内的课本定义为:非0子式的最高阶数......)
秩为1表示变换后的直线落在一条一维的线上,秩为2表示为二维空间
列空间:所有可能得输出向量所构成的集合——所以秩也可以定义为列空间的维数
满秩:秩数与列数相等
12.非方阵的矩阵

如上图,结合一个具体的例子产生矩阵的数值意义:2列代表着,输入空间有两个基向量,即该向量的张成空间可以理解为是二维的;而3行,又意味着每一个基向量又有3个坐标组成。而这样一个三行两列的句子,意味着空间中的一个平面。
总的来说,矩阵的行数即为当前向量坐标的个数,而列数则是基向量的个数~

因此这里提出一个比较炸裂的理解:为什么不是方阵的矩阵均没有行列式呢?这是因为,方阵与向量的积不会改变向量的维度,而矩阵本身又是一个线性变换,所以可以理解为乘以对应的行列式——即某个倍数;而矩阵乘以一个向量,会改变向量的维度!因此在不同的维度下讨论倍数,便不再具有意义。这里打个比方,有一桶水,所谓的伸缩本质上就是给水桶里添加/减少容量的过程,而如果水洒了一地,维度改变,即不再具有倍数的讨论。
13.特征值与特征向量
特征值:衡量特征向量在变换中拉伸或压缩的比例的因子~
特征向量:线性变换中不离开自己张成空间的特殊向量~
(一部分暂不展开更细的讲解,之后有机会更新)