---

偏微分方程(Partial Differential Equation I)
偏微分方程(Partial Differential Equation II)
偏微分方程(Partial Differential Equation III)
偏微分方程(Partial Differential Equation IV)

---

参考文献：

《数学物理方程》| 季孝达
《数学物理方法》| 吴崇试
《数学物理方法》| 梁昆淼
MOOC北京大学《数学物理方法》| 吴崇试 、高春媛

正交曲面坐标系下的分离变量

上章只是讨论了用分离变量法解决直角坐标系中的各种定解问题，但实际中的边界是多种多样的，坐标系参照问题中的边界形状来选择，可以方便的解决相应的本征值问题。

平面极坐标系 ( r , ϕ ) (r,ϕ) (r,ϕ)
{ x = r cos ⁡ ϕ y = r sin ⁡ ϕ \begin{cases} x=r\cosϕ \\ y=r\sinϕ \end{cases} {x=rcosϕy=rsinϕ​

拉普拉斯算符
Δ = ∂ 2 ∂ r 2 + 1 r ∂ ∂ r + 1 r 2 ∂ 2 ∂ ϕ 2 = 1 r ∂ ∂ r ( r ∂ ∂ r ) + 1 r 2 ∂ 2 ∂ ϕ 2 \begin{aligned} Δ &=\cfrac{∂^2}{∂r^2}+\cfrac{1}{r}\cfrac{∂}{∂r}+\cfrac{1}{r^2}\cfrac{∂^2}{∂ϕ^2} \\ &=\cfrac{1}{r}\cfrac{∂}{∂r}\left(r\cfrac{∂}{∂r}\right)+\cfrac{1}{r^2}\cfrac{∂^2}{∂ϕ^2} \end{aligned} Δ​=∂r2∂2​+r1​∂r∂​+r21​∂ϕ2∂2​=r1​∂r∂​(r∂r∂​)+r21​∂ϕ2∂2​​
三维柱坐标系 ( r , ϕ , z ) (r,ϕ,z) (r,ϕ,z)
{ x = r cos ⁡ ϕ y = r sin ⁡ ϕ z = z \begin{cases}x=r\cosϕ \\y=r\sinϕ \\z=z \end{cases} ⎩⎪⎨⎪⎧​x=rcosϕy=rsinϕz=z​

拉普拉斯算符
Δ = ∂ 2 ∂ r 2 + 1 r ∂ ∂ r + 1 r 2 ∂ 2 ∂ ϕ 2 + ∂ 2 ∂ z 2 = 1 r ∂ ∂ r ( r ∂ ∂ r ) + 1 r 2 ∂ 2 ∂ ϕ 2 + ∂ 2 ∂ z 2 \begin{aligned} Δ &=\cfrac{∂^2}{∂r^2}+\cfrac{1}{r}\cfrac{∂}{∂r} +\cfrac{1}{r^2}\cfrac{∂^2}{∂ϕ^2}+\cfrac{∂^2}{∂z^2} \\ &=\cfrac{1}{r}\cfrac{∂}{∂r}\left(r\cfrac{∂}{∂r}\right) +\cfrac{1}{r^2}\cfrac{∂^2}{∂ϕ^2}+\cfrac{∂^2}{∂z^2} \end{aligned} Δ​=∂r2∂2​+r1​∂r∂​+r21​∂ϕ2∂2​+∂z2∂2​=r1​∂r∂​(r∂r∂​)+r21​∂ϕ2∂2​+∂z2∂2​​
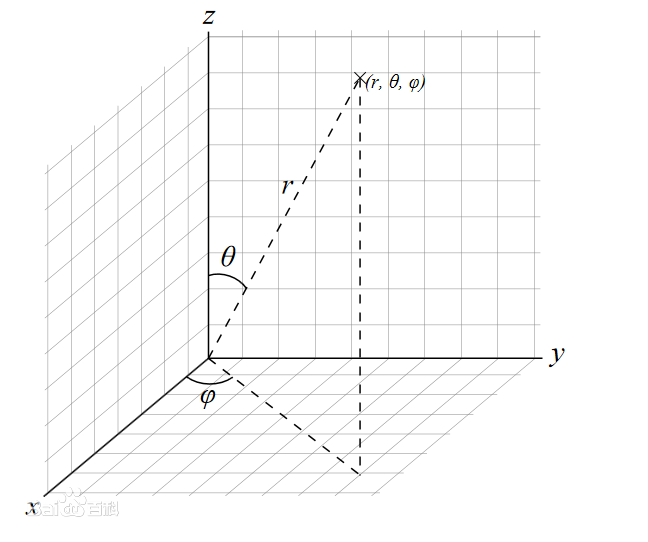
三维球坐标系 ( r , θ , ϕ ) (r,θ,ϕ) (r,θ,ϕ)
{ x = r sin ⁡ θ cos ⁡ ϕ y = r sin ⁡ θ sin ⁡ ϕ z = r cos ⁡ θ \begin{cases} x=r\sinθ\cosϕ \\ y=r\sinθ\sinϕ \\ z=r\cosθ \end{cases} ⎩⎪⎨⎪⎧​x=rsinθcosϕy=rsinθsinϕz=rcosθ​

拉普拉斯算符
Δ = ∂ 2 ∂ r 2 + 2 r ∂ ∂ r + 1 r 2 ∂ 2 ∂ θ 2 + cos ⁡ θ r 2 sin ⁡ θ ∂ ∂ θ + 1 r 2 sin ⁡ 2 θ ∂ 2 ∂ ϕ 2 = 1 r 2 ∂ ∂ r ( r 2 ∂ ∂ r ) + 1 r 2 sin ⁡ θ ∂ ∂ θ ( sin ⁡ θ ∂ ∂ θ ) + 1 r 2 sin ⁡ 2 θ ∂ 2 ∂ ϕ 2 \begin{aligned} Δ & =\cfrac{∂^2}{∂r^2}+\cfrac{2}{r}\cfrac{∂}{∂r} +\cfrac{1}{r^2}\cfrac{∂^2}{∂θ^2} +\cfrac{\cosθ}{r^2\sinθ}\cfrac{∂}{∂θ} +\cfrac{1}{r^2\sin^2θ}\cfrac{∂^2}{∂ϕ^2} \\ &=\cfrac{1}{r^2}\cfrac{∂}{∂r}\left(r^2\cfrac{∂}{∂r}\right) +\cfrac{1}{r^2\sinθ}\cfrac{∂}{∂θ}\left(\sinθ\cfrac{∂}{∂θ}\right) +\cfrac{1}{r^2\sin^2θ}\cfrac{∂^2}{∂ϕ^2} \end{aligned} Δ​=∂r2∂2​+r2​∂r∂​+r21​∂θ2∂2​+r2sinθcosθ​∂θ∂​+r2sin2θ1​∂ϕ2∂2​=r21​∂r∂​(r2∂r∂​)+r2sinθ1​∂θ∂​(sinθ∂θ∂​)+r2sin2θ1​∂ϕ2∂2​​

三维空间拉普拉斯方程
Δ = u x x + u y y + u z z = 0 Δ=u_{xx}+u_{yy}+u_{zz}=0 Δ=uxx​+uyy​+uzz​=0
(1) 球坐标系
1 r 2 ∂ ∂ r ( r 2 ∂ u ∂ r ) + 1 r 2 sin ⁡ θ ∂ ∂ θ ( sin ⁡ θ ∂ u ∂ θ ) + 1 r 2 sin ⁡ 2 θ ∂ 2 u ∂ ϕ 2 = 0 \cfrac{1}{r^2}\cfrac{∂}{∂r}\left(r^2\cfrac{∂u}{∂r}\right) +\cfrac{1}{r^2\sinθ}\cfrac{∂}{∂θ}\left(\sinθ\cfrac{∂u}{∂θ}\right) +\cfrac{1}{r^2\sin^2θ}\cfrac{∂^2u}{∂ϕ^2}=0 r21​∂r∂​(r2∂r∂u​)+r2sinθ1​∂θ∂​(sinθ∂θ∂u​)+r2sin2θ1​∂ϕ2∂2u​=0
令 u ( r , θ , ϕ ) = R ( r ) S ( θ , ϕ ) u(r,θ,ϕ)=R(r)S(θ,ϕ) u(r,θ,ϕ)=R(r)S(θ,ϕ) 带入方程分离变量，可得到
1 R d d r ( r 2 d R d r ) = − 1 S sin ⁡ θ ∂ ∂ θ ( sin ⁡ θ ∂ S ∂ θ ) − 1 S sin ⁡ 2 θ ∂ 2 S ∂ ϕ 2 = μ \cfrac{1}{R}\cfrac{d}{dr}\left(r^2\cfrac{dR}{dr}\right) =-\cfrac{1}{S\sinθ}\cfrac{∂}{∂θ}\left(\sinθ\cfrac{∂S}{∂θ}\right) -\cfrac{1}{S\sin^2θ}\cfrac{∂^2S}{∂ϕ^2}=μ R1​drd​(r2drdR​)=−Ssinθ1​∂θ∂​(sinθ∂θ∂S​)−Ssin2θ1​∂ϕ2∂2S​=μ
于是得到两个方程
d d r ( r 2 d R d r ) − μ R = 0 \cfrac{d}{dr}\left(r^2\cfrac{dR}{dr}\right)-μR=0 drd​(r2drdR​)−μR=0

1 sin ⁡ θ ∂ ∂ θ ( sin ⁡ θ ∂ S ∂ θ ) + 1 sin ⁡ 2 θ ∂ 2 S ∂ ϕ 2 + μ S = 0 \cfrac{1}{\sinθ}\cfrac{∂}{∂θ}\left(\sinθ\cfrac{∂S}{∂θ}\right) +\cfrac{1}{\sin^2θ}\cfrac{∂^2S}{∂ϕ^2}+μS=0 sinθ1​∂θ∂​(sinθ∂θ∂S​)+sin2θ1​∂ϕ2∂2S​+μS=0

第一个常微分方程为欧拉方程，此方程通解为 （取 μ = m 2 μ=m^2 μ=m2 ）
R = { C 0 + D 0 ln ⁡ r ( m = 0 ) C m r m + D m 1 r m ( m ≠ 0 ) R=\begin{cases}C_0+D_0\ln r & (m=0)\\C_mr^m+D_m\cfrac{1}{r^m} & (m\neq0) \end{cases} R=⎩⎨⎧​C0​+D0​lnrCm​rm+Dm​rm1​​(m=0)(m​=0)​
再令 S ( θ , ϕ ) = Θ ( θ ) Φ ( ϕ ) S(θ,ϕ)=Θ(θ)Φ(ϕ) S(θ,ϕ)=Θ(θ)Φ(ϕ) 进一步分离变量，得到
sin ⁡ θ Θ d d θ ( sin ⁡ θ d Θ d θ ) + μ sin ⁡ 2 θ = − 1 Φ d 2 Φ d ϕ 2 = λ \cfrac{\sinθ}{Θ}\cfrac{d}{dθ}\left(\sinθ\cfrac{dΘ}{dθ}\right) +μ\sin^2θ=-\cfrac{1}{Φ}\cfrac{d^2Φ}{dϕ^2}=λ Θsinθ​dθd​(sinθdθdΘ​)+μsin2θ=−Φ1​dϕ2d2Φ​=λ
同样分解为两个常微分方程
Φ ′ ′ + λ Φ = 0 (1.1) Φ''+λΦ=0\tag{1.1} Φ′′+λΦ=0(1.1)

sin ⁡ θ d d θ ( sin ⁡ θ d Θ d θ ) + ( μ sin ⁡ 2 θ − λ ) Θ = 0 (1.2) \sinθ\cfrac{d}{dθ}\left(\sinθ\cfrac{dΘ}{dθ}\right)+(μ\sin^2θ-λ)Θ=0 \tag{1.2} sinθdθd​(sinθdθdΘ​)+(μsin2θ−λ)Θ=0(1.2)

常微分方程 (1.1) 与隐藏的自然周期条件构成本征值问题。易求得本征值是
λ = m 2 , ( m = 0 , 1 , 2 , ⋯   ) λ=m^2,\quad(m=0,1,2,\cdots) λ=m2,(m=0,1,2,⋯)
本征函数为
Φ ( ϕ ) = A cos ⁡ m ϕ + B sin ⁡ m ϕ Φ(ϕ)=A\cos mϕ+B\sin mϕ Φ(ϕ)=Acosmϕ+Bsinmϕ
将本征值带入方程 1.2) ，并做转换 令 x = cos ⁡ θ x=\cosθ x=cosθ ，常数 μ = l ( l + 1 ) μ=l(l+1) μ=l(l+1) 可得到
( 1 − x 2 ) d 2 Θ d x 2 − 2 x d Θ d x + [ l ( l + 1 ) − m 2 1 − x 2 ] Θ = 0 (1-x^2)\cfrac{d^2Θ}{dx^2}-2x\cfrac{dΘ}{dx}+[l(l+1)-\cfrac{m^2}{1-x^2}]Θ=0 (1−x2)dx2d2Θ​−2xdxdΘ​+[l(l+1)−1−x2m2​]Θ=0
这叫做 l l l 阶连带勒让德方程 (Legendre)。其 m = 0 m=0 m=0 的特例叫做勒让德方程。

(2) 柱坐标系
1 r ∂ ∂ r ( r ∂ u ∂ r ) + 1 r 2 ∂ 2 u ∂ ϕ 2 + ∂ 2 u ∂ z 2 = 0 \cfrac{1}{r}\cfrac{∂}{∂r}\left(r\cfrac{∂u}{∂r}\right) +\cfrac{1}{r^2}\cfrac{∂^2u}{∂ϕ^2}+\cfrac{∂^2u}{∂z^2}=0 r1​∂r∂​(r∂r∂u​)+r21​∂ϕ2∂2u​+∂z2∂2u​=0
令 u ( r , ϕ , z ) = R ( r ) Φ ( ϕ ) Z ( z ) u(r,ϕ,z)=R(r)Φ(ϕ)Z(z) u(r,ϕ,z)=R(r)Φ(ϕ)Z(z) 带入方程分离变量，可得到
r 2 R R ′ ′ + r R R ′ + r 2 Z ′ ′ Z = − Φ ′ ′ Φ = λ \cfrac{r^2}{R}R''+\cfrac{r}{R}R'+r^2\cfrac{Z''}{Z}=-\cfrac{Φ''}{Φ}=λ Rr2​R′′+Rr​R′+r2ZZ′′​=−ΦΦ′′​=λ
于是分解为两个方程
Φ ′ ′ + λ Φ = 0 (1.3) Φ''+λΦ=0\tag{1.3} Φ′′+λΦ=0(1.3)

r 2 R R ′ ′ + r R R ′ + r 2 Z ′ ′ Z = λ (1.4) \cfrac{r^2}{R}R''+\cfrac{r}{R}R'+r^2\cfrac{Z''}{Z}=λ\tag{1.4} Rr2​R′′+Rr​R′+r2ZZ′′​=λ(1.4)

方程 (1.4) 同样分解为两个常微分方程
Z ′ ′ + μ Z = 0 (1.5) Z''+μZ=0\tag{1.5} Z′′+μZ=0(1.5)

R ′ ′ + 1 r R ′ − ( μ + λ r 2 ) R = 0 (1.6) R''+\cfrac{1}{r}R'-(μ+\cfrac{λ}{r^2})R=0\tag{1.6} R′′+r1​R′−(μ+r2λ​)R=0(1.6)

常微分方程 (1.3) 与隐藏的自然周期条件构成本征值问题。易求得本征值是
λ = m 2 , ( m = 0 , 1 , 2 , ⋯   ) λ=m^2,\quad(m=0,1,2,\cdots) λ=m2,(m=0,1,2,⋯)
本征函数为
Φ ( ϕ ) = A cos ⁡ m ϕ + B sin ⁡ m ϕ Φ(ϕ)=A\cos mϕ+B\sin mϕ Φ(ϕ)=Acosmϕ+Bsinmϕ
一般，圆柱区域上下底面齐次边界条件或圆柱侧面齐次边界条件分别与 (1.5) 和 (1.6) 构成本征值问题。
方程 (1.5) 的通解为
Z = { C e − μ z + D e − − μ z ( μ < 0 ) C + D z ( μ = 0 ) C cos ⁡ μ z + D sin ⁡ μ z ( μ > 0 ) Z=\begin{cases} Ce^{\sqrt{-μ}z}+De^{-\sqrt{-μ}z} & (μ<0)\\ C+Dz & (μ=0)\\ C\cos\sqrt{μ}z+D\sin\sqrt{μ}z & (μ>0) \end{cases} Z=⎩⎪⎨⎪⎧​Ce−μ ​z+De−−μ ​zC+DzCcosμ ​z+Dsinμ ​z​(μ<0)(μ=0)(μ>0)​
对于方程 (1.6) 分为三种情形
(1) 当 μ = 0 μ=0 μ=0 ，方程为欧拉方程，通解为
R = { E + F ln ⁡ r ( m = 0 ) E r m + F r m ( m = 1 , 2 , ⋯   ) R=\begin{cases} E+F\ln r & (m=0)\\ Er^m+\cfrac{F}{r^m} &(m=1,2,\cdots) \end{cases} R=⎩⎨⎧​E+FlnrErm+rmF​​(m=0)(m=1,2,⋯)​
(2) 当 μ < 0 μ<0 μ<0 取 μ = − ν 2 , x = ν r μ=−ν^2, x=νr μ=−ν2,x=νr 得到 m m m 阶贝塞尔方程 (Bessel)
x 2 d 2 R d x 2 + x d R d x + ( x 2 − m 2 ) R = 0 x^2\cfrac{d^2R}{dx^2}+x\cfrac{dR}{dx}+(x^2-m^2)R=0 x2dx2d2R​+xdxdR​+(x2−m2)R=0
(3) 当 μ > 0 μ>0 μ>0 取 x = μ r x=\sqrt{μ}r x=μ ​r 得到 m m m 阶虚宗量贝塞尔方程
x 2 d 2 R d x 2 + x d R d x − ( x 2 + m 2 ) R = 0 x^2\cfrac{d^2R}{dx^2}+x\cfrac{dR}{dx}-(x^2+m^2)R=0 x2dx2d2R​+xdxdR​−(x2+m2)R=0
波动方程
u t t − a 2 Δ u = 0 u_{tt}-a^2Δu=0 utt​−a2Δu=0
分离时间变量 t t t 和空间变量 r \mathrm{r} r ，令 u ( r , t ) = T ( t ) v ( r ) u(\mathrm{r},t)=T(t)v(\mathrm{r}) u(r,t)=T(t)v(r) 带入方程得到
T ′ ′ a 2 T = Δ v v = − k 2 \cfrac{T''}{a^2T}=\cfrac{Δv}{v}=-k^2 a2TT′′​=vΔv​=−k2
于是分解为两个方程
T ′ ′ + k 2 a 2 T = 0 (1.7) T''+k^2a^2T=0\tag{1.7} T′′+k2a2T=0(1.7)

Δ v + k 2 v = 0 (1.8) Δv+k^2v=0\tag{1.8} Δv+k2v=0(1.8)

常微分方程 (1.7) 为已讨论过的欧拉方程，偏微分方程 (1.8) 叫做亥姆霍兹方程。

热传导方程
u t − a 2 Δ u = 0 u_t-a^2 Δu=0 ut​−a2Δu=0
分离时间变量 t t t 和空间变量 r \mathrm{r} r ，令 u ( r , t ) = T ( t ) v ( r ) u(\mathrm{r},t)=T(t)v(\mathrm{r}) u(r,t)=T(t)v(r) 带入方程得到
T ′ a 2 T = Δ v v = − k 2 \cfrac{T'}{a^2T}=\cfrac{Δv}{v}=-k^2 a2TT′​=vΔv​=−k2
于是分解为两个方程
T ′ + k 2 a 2 T = 0 (1.9) T'+k^2a^2T=0\tag{1.9} T′+k2a2T=0(1.9)

Δ v + k 2 v = 0 (1.10) Δv+k^2v=0\tag{1.10} Δv+k2v=0(1.10)

常微分方程 (1.9) 为已讨论过的欧拉方程，偏微分方程 (1.10) 也是亥姆霍兹方程。

亥姆霍兹方程 (Helmholtz)
Δ v + k 2 v = 0 Δv+k^2v=0 Δv+k2v=0
(1) 球坐标系
1 r 2 ∂ ∂ r ( r 2 ∂ v ∂ r ) + 1 r 2 sin ⁡ θ ∂ ∂ θ ( sin ⁡ θ ∂ v ∂ θ ) + 1 r 2 sin ⁡ 2 θ ∂ 2 v ∂ ϕ 2 + k 2 v = 0 \cfrac{1}{r^2}\cfrac{∂}{∂r}\left(r^2\cfrac{∂v}{∂r}\right) +\cfrac{1}{r^2\sinθ}\cfrac{∂}{∂θ}\left(\sinθ\cfrac{∂v}{∂θ}\right) +\cfrac{1}{r^2\sin^2θ}\cfrac{∂^2v}{∂ϕ^2}+k^2v=0 r21​∂r∂​(r2∂r∂v​)+r2sinθ1​∂θ∂​(sinθ∂θ∂v​)+r2sin2θ1​∂ϕ2∂2v​+k2v=0
令 v ( r , θ , ϕ ) = R ( r ) S ( θ , ϕ ) v(r,θ,ϕ)=R(r)S(θ,ϕ) v(r,θ,ϕ)=R(r)S(θ,ϕ) 带入方程分离变量，可得到
d d r ( r 2 d R d r ) + ( k 2 r 2 − μ ) R = 0 (1.11) \cfrac{d}{dr}\left(r^2\cfrac{dR}{dr}\right)+(k^2r^2-μ)R=0\tag{1.11} drd​(r2drdR​)+(k2r2−μ)R=0(1.11)

1 sin ⁡ θ ∂ ∂ θ ( sin ⁡ θ ∂ S ∂ θ ) + 1 sin ⁡ 2 θ ∂ 2 S ∂ ϕ 2 + μ S = 0 (1.12) \cfrac{1}{\sinθ}\cfrac{∂}{∂θ}\left(\sinθ\cfrac{∂S}{∂θ}\right)+\cfrac{1}{\sin^2θ}\cfrac{∂^2S}{∂ϕ^2}+μS=0\tag{1.12} sinθ1​∂θ∂​(sinθ∂θ∂S​)+sin2θ1​∂ϕ2∂2S​+μS=0(1.12)

再令 S ( θ , ϕ ) = Θ ( θ ) Φ ( ϕ ) S(θ,ϕ)=Θ(θ)Φ(ϕ) S(θ,ϕ)=Θ(θ)Φ(ϕ) 进一步分离变量，可得到
Φ ′ ′ + λ Φ = 0 Φ''+λΦ=0 Φ′′+λΦ=0

sin ⁡ θ d d θ ( sin ⁡ θ d Θ d θ ) + ( μ sin ⁡ 2 θ − λ ) Θ = 0 \sinθ\cfrac{d}{dθ}\left(\sinθ\cfrac{dΘ}{dθ}\right)+(μ\sin^2θ-λ)Θ=0 sinθdθd​(sinθdθdΘ​)+(μsin2θ−λ)Θ=0

可以像上节那样进一步得到
Φ ( ϕ ) = A cos ⁡ m ϕ + B sin ⁡ m ϕ ( m = 0 , 1 , 2 , ⋯   ) Φ(ϕ)=A\cos mϕ+B\sin mϕ\quad(m=0,1,2,\cdots) Φ(ϕ)=Acosmϕ+Bsinmϕ(m=0,1,2,⋯)
和 l l l 阶连带勒让德方程
( 1 − x 2 ) d 2 Θ d x 2 − 2 x d Θ d x + [ l ( l + 1 ) − m 2 1 − x 2 ] Θ = 0 (1-x^2)\cfrac{d^2Θ}{dx^2}-2x\cfrac{dΘ}{dx}+[l(l+1)-\cfrac{m^2}{1-x^2}]Θ=0 (1−x2)dx2d2Θ​−2xdxdΘ​+[l(l+1)−1−x2m2​]Θ=0
其中 x = cos ⁡ θ x=\cosθ x=cosθ ，常数 μ = l ( l + 1 ) μ=l(l+1) μ=l(l+1) 。这时，方程 (1.11) 可成为
d d r ( r 2 d R d r ) + [ k 2 r 2 − l ( l + 1 ) ] R = 0 \cfrac{d}{dr}\left(r^2\cfrac{dR}{dr}\right)+[k^2r^2-l(l+1)]R=0 drd​(r2drdR​)+[k2r2−l(l+1)]R=0
叫做 l l l 阶球贝塞尔方程。

(2) 柱坐标系
1 r ∂ ∂ r ( r ∂ v ∂ r ) + 1 r 2 ∂ 2 v ∂ ϕ 2 + ∂ 2 v ∂ z 2 + k 2 v = 0 \cfrac{1}{r}\cfrac{∂}{∂r}\left(r\cfrac{∂v}{∂r}\right)+\cfrac{1}{r^2}\cfrac{∂^2v}{∂ϕ^2}+\cfrac{∂^2v}{∂z^2}+k^2v=0 r1​∂r∂​(r∂r∂v​)+r21​∂ϕ2∂2v​+∂z2∂2v​+k2v=0
令 v ( r , ϕ , z ) = R ( r ) Φ ( ϕ ) Z ( z ) v(r,ϕ,z)=R(r)Φ(ϕ)Z(z) v(r,ϕ,z)=R(r)Φ(ϕ)Z(z) 一步步分离变量，可得到
Φ ′ ′ + λ Φ = 0 (1.13) Φ''+λΦ=0\tag{1.13} Φ′′+λΦ=0(1.13)

Z ′ ′ + μ Z = 0 (1.14) Z''+μZ=0\tag{1.14} Z′′+μZ=0(1.14)

R ′ ′ + 1 r R ′ + ( k 2 − μ − λ r 2 ) R = 0 (1.15) R''+\cfrac{1}{r}R'+(k^2-μ-\cfrac{λ}{r^2})R=0\tag{1.15} R′′+r1​R′+(k2−μ−r2λ​)R=0(1.15)

圆柱区域上下底面齐次边界条件或圆柱侧面齐次边界条件分别与 (1.13) 和 (1.14) 构成本征值问题。
取 x = k 2 − μ r x=\sqrt{k^2-μ}r x=k2−μ ​r ，方程 (1.15) 如上节那样变为 贝塞尔方程 。

球函数

勒让德方程的解

求解勒让德方程(Legendre equation)
( 1 − x 2 ) y ′ ′ − 2 x y ′ + l ( l + 1 ) y = 0 (1.1) (1-x^2)y''-2xy'+l(l+1)y=0\tag{1.1} (1−x2)y′′−2xy′+l(l+1)y=0(1.1)

其中 l l l 为实参数，该方程的任意非零解称为勒让德函数。由于方程是二阶变系数常微分方程，可采用幂级数求解。

易知 x = 0 x=0 x=0 是方程的常点¹，当 ∣ x ∣ < 1 |x|<1 ∣x∣<1 时，方程有幂级数解
y = ∑ k = 0 ∞ c k x k (1.2) y=\displaystyle\sum_{k=0}^∞c_kx^k\tag{1.2} y=k=0∑∞​ck​xk(1.2)

如果系数 p ( x ) , q ( x ) p(x),q(x) p(x),q(x) 在点 x 0 x_0 x0​ 的邻域是解析的，则点 x 0 x_0 x0​ 叫做方程的常点；如果 x 0 x_0 x0​ 是 p ( x ) p(x) p(x) 或 q ( x ) q(x) q(x) 的奇点，则点 x 0 x_0 x0​ 叫做方程的奇点。

带入勒让德方程逐项微分整理合并，可以得到
∑ k = 0 ∞ { ( k + 2 ) ( k + 1 ) c k + 2 − [ k ( k + 1 ) − l ( l + 1 ) ] c k } x k = 0 \displaystyle \sum_{k=0}^∞\{(k+2)(k+1)c_{k+2}-[k(k+1)-l(l+1)]c_k\}x^k=0 k=0∑∞​{(k+2)(k+1)ck+2​−[k(k+1)−l(l+1)]ck​}xk=0
根据泰勒展开的唯一性可以得到
( k + 2 ) ( k + 1 ) c k + 2 − [ k ( k + 1 ) − l ( l + 1 ) ] c k = 0 (k+2)(k+1)c_{k+2}-[k(k+1)-l(l+1)]c_k=0 (k+2)(k+1)ck+2​−[k(k+1)−l(l+1)]ck​=0
即获得递推公式
c k + 2 = ( k − l ) ( k + l + 1 ) ( k + 2 ) ( k + 1 ) c k (1.3) c_{k+2}=\cfrac{(k-l)(k+l+1)}{(k+2)(k+1)}c_k\tag{1.3} ck+2​=(k+2)(k+1)(k−l)(k+l+1)​ck​(1.3)
反复利用递推关系式就可以得到系数
{ c 2 k = c 0 ( 2 k ) ! ( 2 k − l − 2 ) ( 2 k − l − 4 ) ⋯ ( − l ) ( 2 k + l − 1 ) ( 2 k + l − 3 ) ⋯ ( l + 1 ) c 2 k + 1 = c 1 ( 2 k + 1 ) ! ( 2 k − l − 1 ) ( 2 k − l − 3 ) ⋯ ( − l + 1 ) ( 2 k + l ) ( 2 k + l − 2 ) ⋯ ( l + 2 ) \begin{cases} c_{2k}=\cfrac{c_0}{(2k)!}(2k-l-2)(2k-l-4)\cdots(-l)(2k+l-1)(2k+l-3)\cdots(l+1) \\ c_{2k+1}=\cfrac{c_1}{(2k+1)!}(2k-l-1)(2k-l-3)\cdots(-l+1)(2k+l)(2k+l-2)\cdots(l+2) \end{cases} ⎩⎪⎪⎨⎪⎪⎧​c2k​=(2k)!c0​​(2k−l−2)(2k−l−4)⋯(−l)(2k+l−1)(2k+l−3)⋯(l+1)c2k+1​=(2k+1)!c1​​(2k−l−1)(2k−l−3)⋯(−l+1)(2k+l)(2k+l−2)⋯(l+2)​
其中 c 0 , c 1 c_0,c_1 c0​,c1​ 是任意常数。利用 Γ \Gamma Γ 函数²的性质，上式可化为

{ c 2 k = c 0 2 2 k ( 2 k ) ! Γ ( k − l 2 ) Γ ( k + l + 1 2 ) Γ ( − l 2 ) Γ ( l + 1 2 ) c 2 k + 1 = c 1 2 2 k ( 2 k + 1 ) ! Γ ( k − l − 1 2 ) Γ ( k + 1 + l 2 ) Γ ( k − l − 1 2 ) Γ ( 1 + l 2 ) \begin{cases} c_{2k}=c_0\cfrac{2^{2k}}{(2k)!}\cfrac{Γ(k-\cfrac{l}{2})Γ(k+\cfrac{l+1}{2})}{Γ(-\cfrac{l}{2})Γ(\cfrac{l+1}{2})} \\ c_{2k+1}=c_1\cfrac{2^{2k}}{(2k+1)!}\cfrac{Γ(k-\cfrac{l-1}{2})Γ(k+1+\cfrac{l}{2})}{Γ(k-\cfrac{l-1}{2})Γ(1+\cfrac{l}{2})} \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​c2k​=c0​(2k)!22k​Γ(−2l​)Γ(2l+1​)Γ(k−2l​)Γ(k+2l+1​)​c2k+1​=c1​(2k+1)!22k​Γ(k−2l−1​)Γ(1+2l​)Γ(k−2l−1​)Γ(k+1+2l​)​​
此时，分别取 c 0 = 1 , c 1 = 0 c_0=1,c_1=0 c0​=1,c1​=0 和 c 0 = 0 , c 1 = 1 c_0=0,c_1=1 c0​=0,c1​=1 ，我们可以获得两个级数解
y 1 ( x ) = ∑ k = 0 ∞ c 2 k x 2 k (1.4) y_1(x)=\sum_{k=0}^{∞}c_{2k}x^{2k} \tag{1.4} y1​(x)=k=0∑∞​c2k​x2k(1.4)

y 2 ( x ) = ∑ k = 0 ∞ c 2 k + 1 x 2 k + 1 (1.5) y_2(x)=\sum_{k=0}^{∞}c_{2k+1}x^{2k+1}\tag{1.5} y2​(x)=k=0∑∞​c2k+1​x2k+1(1.5)

容易证明 y 1 ( x ) , y 2 ( x ) y_1(x),y_2(x) y1​(x),y2​(x) 线性无关，且在 x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1) 收敛。所以，勒让德方程的解就是
y ( x ) = C 0 y 1 ( x ) + C 1 y 2 ( x ) y(x)=C_0y_1(x)+C_1y_2(x) y(x)=C0​y1​(x)+C1​y2​(x)

其中 C 0 , C 1 C_0,C_1 C0​,C1​ 为任意常数。

勒让德函数

勒让德多项式：观察上节级数 y 1 ( x ) , y 2 ( x ) y_1(x),y_2(x) y1​(x),y2​(x) ，容易发现，如果参数 l l l 是某个偶数 ， l = 2 n l=2n l=2n（ n n n是正整数）， y 1 ( x ) y_1(x) y1​(x) 则直到 x 2 n x^{2n} x2n 为止，因为从 c 2 n + 2 c_{2n+2} c2n+2​ 开始都含有因子 ( 2 n − l ) (2n-l) (2n−l) 从而都为零。 y 1 ( x ) y_1(x) y1​(x) 化为 2 n 2n 2n 次多项式，并且只含偶次幂，而 y 2 ( x ) y_2(x) y2​(x) 仍然是无穷级数。同理，当 l l l 是奇数 ， l = 2 n + 1 l=2n+1 l=2n+1（ n n n是零或正整数）， y 2 ( x ) y_2(x) y2​(x) 化为 2 n + 1 2n+1 2n+1 次多项式，并且只含奇次幂，而 y 1 ( x ) y_1(x) y1​(x) 仍然是无穷级数。
下面给出 y 1 ( x ) y_1(x) y1​(x) 或 y 2 ( x ) y_2(x) y2​(x) 为多项式时的表达式，为了简洁，通常取最高次项的系数（ l l l为零或正整数）
c l = ( 2 l ) ! 2 l ( l ! ) 2 c_{l}=\cfrac{(2l)!}{2^l(l!)^2} cl​=2l(l!)2(2l)!​
反用系数递推公式 (1.3)
c k = ( k + 2 ) ( k + 1 ) ( k − l ) ( k + l + 1 ) c k + 2 c_k=\cfrac{(k+2)(k+1)}{(k-l)(k+l+1)}c_{k+2} ck​=(k−l)(k+l+1)(k+2)(k+1)​ck+2​
就可以把其他系数一一推算出来，一般的有
c l − 2 n = ( − 1 ) n ( 2 l − 2 n ) ! n ! 2 l ( l − n ) ! ( l − 2 n ) ! c_{l-2n}=(-1)^n\cfrac{(2l-2n)!}{n!2^l(l-n)!(l-2n)!} cl−2n​=(−1)nn!2l(l−n)!(l−2n)!(2l−2n)!​
这样求得勒让德方程 (1.1) 的解称为 l l l 阶勒让德多项式，或第一类勒让德函数。
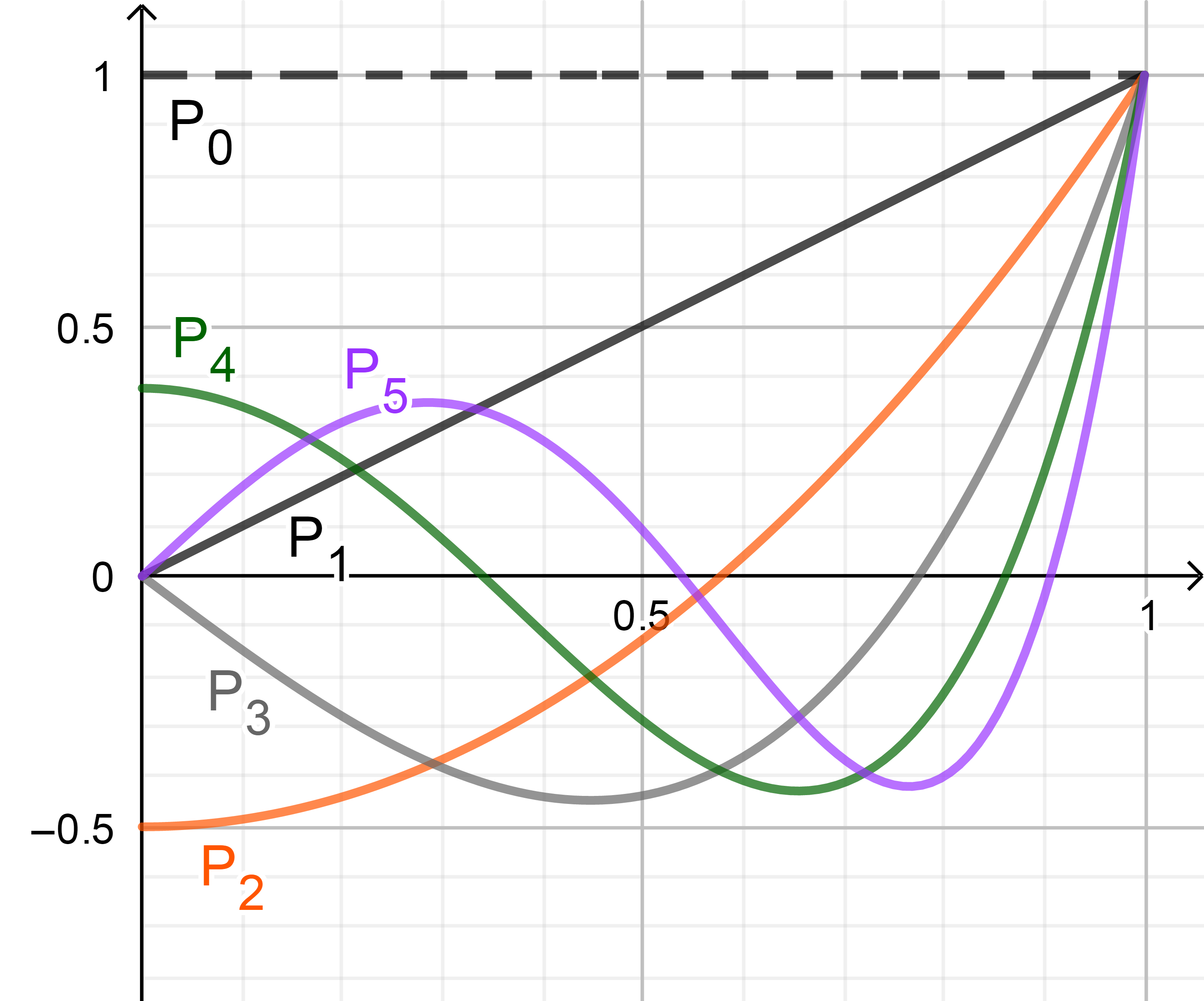
P l ( x ) = ∑ n = 0 [ l / 2 ] ( − 1 ) n ( 2 l − 2 n ) ! n ! 2 l ( l − n ) ! ( l − 2 n ) ! x l − 2 n (2.1) P_l(x)=\sum_{n=0}^{[l/2]}(-1)^n \cfrac{(2l-2n)!}{n!2^l(l-n)!(l-2n)!}x^{l-2n}\tag{2.1} Pl​(x)=n=0∑[l/2]​(−1)nn!2l(l−n)!(l−2n)!(2l−2n)!​xl−2n(2.1)
其中 l l l为零或正整数，记号 [ l / 2 ] [l/2] [l/2] 表示不超过 l / 2 l/2 l/2 的最大整数，即
[ l / 2 ] = { l / 2 ( l 为 偶 数 ) ( l − 1 ) / 2 ( l 为 奇 数 ) [l/2]=\begin{cases} l/2 & (l 为偶数)\\ (l-1)/2 & (l 为奇数) \end{cases} [l/2]={l/2(l−1)/2​(l为偶数)(l为奇数)​

勒让德多项式的微分表示
P l ( x ) = 1 2 l l ! d l d x l ( x 2 − 1 ) l (2.2) P_l(x)=\cfrac{1}{2^ll!}\cfrac{d^l}{dx^l}(x^2-1)^l\tag{2.2} Pl​(x)=2ll!1​dxldl​(x2−1)l(2.2)
此式称为罗德里格斯表达式(Rodrigues)。由表达式不难看出勒让德多项式的奇偶性
P l ( − x ) = ( − 1 ) l P l ( x ) P_l(-x)=(-1)^lP_l(x) Pl​(−x)=(−1)lPl​(x)

勒让德多项式的积分表示：按照柯西公式，微分表示可写成路径积分
P l ( x ) = 1 2 π i 1 2 l ∮ C ( z 2 − 1 ) l ( z − x ) l + 1 d z (2.3) P_l(x)=\cfrac{1}{2\pi\mathrm i}\cfrac{1}{2^l}\oint_C\cfrac{(z^2-1)^l}{(z-x)^{l+1}}dz\tag{2.3} Pl​(x)=2πi1​2l1​∮C​(z−x)l+1(z2−1)l​dz(2.3)
其中 C C C 为 z z z 平面上围绕 z = x z=x z=x 点任一闭合回路，这叫做施列夫利积分 (SchlMli)。
还可以进一步表示为定积分，为此取 C C C 为圆周，圆心在 z = x z=x z=x ，半径为 x 2 − 1 \sqrt{x^2-1} x2−1 ​ 。在圆周 C C C 上 z − x = x 2 − 1 e i ψ , d z = i x 2 − 1 e i ψ d ψ z-x=\sqrt{x^2-1}e^{\mathrm iψ},dz=\mathrm i\sqrt{x^2-1}e^{\mathrm iψ}dψ z−x=x2−1 ​eiψ,dz=ix2−1 ​eiψdψ ，所以 (2.3) 式成为
P l ( x ) = 1 π ∫ 0 π [ x + i 1 − x 2 cos ⁡ ψ ] l d ψ P_l(x)=\cfrac{1}{\pi}\int_0^{\pi}[x+\mathrm i\sqrt{1-x^2}\cos\mathrm ψ]^ldψ Pl​(x)=π1​∫0π​[x+i1−x2 ​cosψ]ldψ
这叫做拉普拉斯积分，如果从 x x x 变换回变量 θ ,   x = cos ⁡ θ θ,\ x=\cosθ θ, x=cosθ ，则
P l ( x ) = 1 π ∫ 0 π [ cos ⁡ θ + i sin ⁡ θ cos ⁡ ψ ] l d ψ (2.4) P_l(x)=\cfrac{1}{\pi}\int_0^{\pi}[\cosθ+\mathrm i\sinθ\cos\mathrm ψ]^ldψ\tag{2.4} Pl​(x)=π1​∫0π​[cosθ+isinθcosψ]ldψ(2.4)
从上式很容易看出 P l ( 1 ) = 1 , P l ( − 1 ) = ( − 1 ) l P_l(1)=1,P_l(-1)=(-1)^l Pl​(1)=1,Pl​(−1)=(−1)l 从而得到
∣ P l ( x ) ∣ ⩽ 1 , ( − 1 ⩽ x ⩽ 1 ) |P_l(x)|⩽1,\quad(-1⩽x⩽1) ∣Pl​(x)∣⩽1,(−1⩽x⩽1)

第二类勒让德函数：以上讨论知道，当 l l l为零或正整数时， y 1 , y 2 y_1,y_2 y1​,y2​ 中有一个是勒让德多项式，而另一个仍是无穷级数，此时勒让德方程的一般解为
y = C 1 P l ( x ) + C 2 Q l ( x ) y=C_1P_l(x)+C_2Q_l(x) y=C1​Pl​(x)+C2​Ql​(x)
其中 Q l ( x ) Q_l(x) Ql​(x) 为由 P l ( x ) P_l(x) Pl​(x) 导出具有统一形式的线性无关特解
Q l ( x ) = P l ( x ) ∫ 1 ( 1 − x 2 ) P l 2 ( x ) d x (2.5) Q_l(x)=P_l(x)\int\cfrac{1}{(1-x^2)P_l^2(x)}dx\tag{2.5} Ql​(x)=Pl​(x)∫(1−x2)Pl2​(x)1​dx(2.5)
可计算得 Q 0 ( x ) = 1 2 ln ⁡ 1 + x 1 − x , Q 1 ( x ) = x 2 ln ⁡ 1 + x 1 − x − 1 , ⋯ Q_0(x)=\cfrac{1}{2}\ln\cfrac{1+x}{1-x},\quad Q_1(x)=\cfrac{x}{2}\ln\cfrac{1+x}{1-x}-1,\quad \cdots Q0​(x)=21​ln1−x1+x​,Q1​(x)=2x​ln1−x1+x​−1,⋯
一般表达式为
Q l ( x ) = 1 2 P l ( x ) ln ⁡ 1 + x 1 − x − ∑ n = 1 [ l / 2 ] 2 l − 4 n + 3 ( 2 n − 1 ) ( l − n + 1 ) P l − 2 n + 1 ( x ) (2.6) Q_l(x)=\cfrac{1}{2}P_l(x)\ln\cfrac{1+x}{1-x} -\sum_{n=1}^{[l/2]}\cfrac{2l-4n+3}{(2n-1)(l-n+1)}P_{l-2n+1}(x)\tag{2.6} Ql​(x)=21​Pl​(x)ln1−x1+x​−n=1∑[l/2]​(2n−1)(l−n+1)2l−4n+3​Pl−2n+1​(x)(2.6)

勒让德多项式的正交性：在区间 ( − 1 , 1 ) (-1,1) (−1,1) 上正交
∫ − 1 1 P l ( x ) P k ( x ) d x = 0 ( l ≠ k ) \int_{-1}^{1}P_l(x)P_k(x)dx=0\quad(l\neq k) ∫−11​Pl​(x)Pk​(x)dx=0(l​=k)
如果从 x x x 变换回变量 θ ,   x = cos ⁡ θ θ,\ x=\cosθ θ, x=cosθ ，则
∫ 0 π P l ( cos ⁡ θ ) P k ( cos ⁡ θ ) sin ⁡ θ d θ = 0 ( l ≠ k ) \int_{0}^{\pi}P_l(\cosθ)P_k(\cosθ)\sinθdθ=0\quad(l\neq k) ∫0π​Pl​(cosθ)Pk​(cosθ)sinθdθ=0(l​=k)

勒让德多项式的模
∥ P l ( x ） ∥ 2 = ∫ − 1 1 P l 2 ( x ) d x \|P_l(x）\|^2=\int_{-1}^{1}P^2_l(x)dx ∥Pl​(x）∥2=∫−11​Pl2​(x)dx
可计算得
∥ P l ( x ） ∥ = 2 2 l + 1 ( l = 0 , 1 , 2 , ⋯   ) (2.7) \|P_l(x）\|=\sqrt{\cfrac{2}{2l+1}}\quad(l=0,1,2,\cdots)\tag{2.7} ∥Pl​(x）∥=2l+12​ ​(l=0,1,2,⋯)(2.7)

傅里叶-勒让德级数：设函数 f ( x ) f(x) f(x) 在区间 [ − 1 , 1 ] [-1,1] [−1,1] 上满足狄利克雷条件，则 f ( x ) f(x) f(x) 在连续点处展开为
f ( x ) = ∑ k = 0 ∞ c k P k ( x ) f(x)=\sum_{k=0}^{\infty}c_kP_k(x) f(x)=k=0∑∞​ck​Pk​(x)
其中系数
c k = 2 k + 1 2 ∫ − 1 1 f ( x ) P k ( x ) d x c_k=\cfrac{2k+1}{2}\int_{-1}^{1}f(x)P_k(x)dx ck​=22k+1​∫−11​f(x)Pk​(x)dx
在物理上常取 x = cos ⁡ θ ( 0 ⩽ θ ⩽ π ) x=\cosθ(0⩽θ⩽\pi) x=cosθ(0⩽θ⩽π) ，则
f ( θ ) = ∑ k = 0 ∞ c k P k ( cos ⁡ θ ) f(θ)=\sum_{k=0}^{\infty}c_kP_k(\cosθ) f(θ)=k=0∑∞​ck​Pk​(cosθ)
其中系数
c k = 2 k + 1 2 ∫ 0 π f ( θ ) P k ( cos ⁡ θ ) sin ⁡ θ d θ c_k=\cfrac{2k+1}{2}\int_{0}^{\pi}f(θ)P_k(\cosθ)\sinθdθ ck​=22k+1​∫0π​f(θ)Pk​(cosθ)sinθdθ

勒让德多项式的生成函数：首先由电荷势理论引入
1 R 2 − 2 R r cos ⁡ θ + r 2 = { ∑ k = 0 ∞ r k R k + 1 P k ( cos ⁡ θ ) ( r < R ) ∑ k = 0 ∞ R k r k + 1 P k ( cos ⁡ θ ) ( r > R ) (2.8) \cfrac{1}{\sqrt{R^2-2Rr\cosθ+r^2}}=\begin{cases} \displaystyle\sum_{k=0}^{\infty}\cfrac{r^k}{R^{k+1}}P_k(\cosθ) &(r<R) \\ \displaystyle\sum_{k=0}^{\infty}\cfrac{R^k}{r^{k+1}}P_k(\cosθ) &(r>R) \end{cases} \tag{2.8} R2−2Rrcosθ+r2 ​1​=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧​k=0∑∞​Rk+1rk​Pk​(cosθ)k=0∑∞​rk+1Rk​Pk​(cosθ)​(r<R)(r>R)​(2.8)

勒让德多项式的递推关系
(1) 递推公式
( k + 1 ) P k + 1 ( x ) − ( 2 k + 1 ) x P k ( x ) + k P k − 1 ( x ) = 0 (2.9) (k+1)P_{k+1}(x)-(2k+1)xP_k(x)+kP_{k-1}(x)=0\tag{2.9} (k+1)Pk+1​(x)−(2k+1)xPk​(x)+kPk−1​(x)=0(2.9)
(2) 通过微分还可以获得许多其他类别的递推关系
P k ′ ( x ) − x P k − 1 ′ ( x ) = k P k − 1 ( x ) P k ′ ( x ) − P k − 1 ′ ( x ) = k P k ( x ) ( 1 − x 2 ) P k ′ ( x ) = k P k − 1 ′ ( x ) − k x P k ( x ) ( 1 − x 2 ) P k − 1 ′ ( x ) = k x P k − 1 ( x ) − k P k ′ ( x ) P'_k(x)-xP'_{k-1}(x)=kP_{k-1}(x) \\ P'_k(x)-P'_{k-1}(x)=kP_{k}(x) \\ (1-x^2)P'_k(x)=kP'_{k-1}(x)-kxP_{k}(x) \\ (1-x^2)P'_{k-1}(x)=kxP_{k-1}(x)-kP'_{k}(x) Pk′​(x)−xPk−1′​(x)=kPk−1​(x)Pk′​(x)−Pk−1′​(x)=kPk​(x)(1−x2)Pk′​(x)=kPk−1′​(x)−kxPk​(x)(1−x2)Pk−1′​(x)=kxPk−1​(x)−kPk′​(x)

勒让德多项式的奇偶性：当 l l l 为偶数时， P l ( x ) P_l(x) Pl​(x) 为偶函数；当 l l l 为奇数时， P l ( x ) P_l(x) Pl​(x) 为奇函数
P l ( − x ) = ( − 1 ) l P l ( x ) (2.10) P_l(-x)=(-1)^lP_l(x)\tag{2.10} Pl​(−x)=(−1)lPl​(x)(2.10)

连带勒让德函数

连带勒让德方程
( 1 − x 2 ) d 2 Θ d x 2 − 2 x d Θ d x + [ l ( l + 1 ) − m 2 1 − x 2 ] Θ = 0 (3.1) (1-x^2)\cfrac{d^2Θ}{dx^2}-2x\cfrac{dΘ}{dx}+[l(l+1)-\cfrac{m^2}{1-x^2}]Θ=0\tag{3.1} (1−x2)dx2d2Θ​−2xdxdΘ​+[l(l+1)−1−x2m2​]Θ=0(3.1)
为了寻找连带勒让德方程和勒让德方程之间的联系，通常作代换
Θ = ( 1 − x 2 ) m / 2 y ( x ) Θ=(1-x^2)^{m/2}y(x) Θ=(1−x2)m/2y(x)
则方程 (3.1) 可化为
( 1 − x 2 ) y ′ ′ − 2 ( m + 1 ) x y ′ + [ l ( l + 1 ) − m ( m + 1 ) ] y = 0 (3.2) (1-x^2)y''-2(m+1)xy'+[l(l+1)-m(m+1)]y=0\tag{3.2} (1−x2)y′′−2(m+1)xy′+[l(l+1)−m(m+1)]y=0(3.2)
事实上，上述微分方程 (3.2) 就是勒让德方程求导 m m m 次得到的方程，利用莱布尼茨求导公式
( u v ) ( n ) = ∑ k = 0 n ∁ n k u ( n − k ) v ( k ) (uv)^{(n)}=\displaystyle\sum_{k=0}^n ∁^k_n u^{(n-k)}v^{(k)} (uv)(n)=k=0∑n​∁nk​u(n−k)v(k)
将勒让德方程
( 1 − x 2 ) P ′ ′ − 2 x P ′ + l ( l + 1 ) P = 0 (1-x^2)P''-2xP'+l(l+1)P=0 (1−x2)P′′−2xP′+l(l+1)P=0
对 x x x 求导 m m m 次得到
( 1 − x 2 ) ( P ( m ) ) ′ ′ − 2 x ( P ( m ) ) ′ + [ l ( l + 1 ) − m ( m + 1 ) ] P ( m ) = 0 (1-x^2)(P^{(m)})''-2x(P^{(m)})'+[l(l+1)-m(m+1)]P^{(m)}=0 (1−x2)(P(m))′′−2x(P(m))′+[l(l+1)−m(m+1)]P(m)=0
这正是方程 (3.2) 的形式，因此方程 (3.2) 的解 y ( x ) y(x) y(x) 正是勒让德方程解 P ( x ) P(x) P(x) 的 m m m 阶导数。方程 (3.2) 与自然边界条件构成本征值问题，本征值是 l ( l + 1 ) l(l+1) l(l+1) ，本征函数则是勒让德多项式 P l ( x ) P_l(x) Pl​(x) 的 m m m 阶导数，即
y ( x ) = P l ( m ) ( x ) y(x)=P_l^{(m)}(x) y(x)=Pl(m)​(x)
将此式代回可得到 Θ = ( 1 − x 2 ) m / 2 P l ( m ) ( x ) Θ=(1-x^2)^{m/2}P_l^{(m)}(x) Θ=(1−x2)m/2Pl(m)​(x) ，通常记作
P l m ( x ) = ( 1 − x 2 ) m / 2 P l ( m ) ( x ) (3.3) P_l^m(x)=(1-x^2)^{m/2}P_l^{(m)}(x)\tag{3.3} Plm​(x)=(1−x2)m/2Pl(m)​(x)(3.3)
这称为连带勒让德多项式。由于 P l ( x ) P_l(x) Pl​(x) 是 l l l 次多项式，最多只能求导 l l l 次，超过后就得到零，因此必须有 l ⩾ m l⩾m l⩾m 。

连带勒让德多项式的微分表示
P l m ( x ) = ( 1 − x 2 ) m / 2 2 l l ! d l + m d x l + m ( x 2 − 1 ) l (3.4) P^m_l(x)=\cfrac{(1-x^2)^{m/2}}{2^ll!}\cfrac{d^{l+m}}{dx^{l+m}}(x^2-1)^l\tag{3.4} Plm​(x)=2ll!(1−x2)m/2​dxl+mdl+m​(x2−1)l(3.4)
此式称为罗德里格斯表达式(Rodrigues)。

连带勒让德多项式的积分表示：按照柯西公式，微分表示可写成路径积分
P l m ( x ) = ( 1 − x 2 ) m / 2 2 l 1 2 π i ( l + m ) ! l ! ∮ C ( z 2 − 1 ) l ( z − x ) l + m + 1 d z (3.5) P^m_l(x)=\cfrac{(1-x^2)^{m/2}}{2^l} \cfrac{1}{2\pi\mathrm i}\cfrac{(l+m)!}{l!} \oint_C\cfrac{(z^2-1)^l}{(z-x)^{l+m+1}}dz\tag{3.5} Plm​(x)=2l(1−x2)m/2​2πi1​l!(l+m)!​∮C​(z−x)l+m+1(z2−1)l​dz(3.5)
其中 C C C 为 z z z 平面上围绕 z = x z=x z=x 点任一闭合回路，这叫做施列夫利积分 (SchlMli)。
还可以进一步表示为
P l m ( x ) = i m 2 π ( l + m ) ! l ! ∫ − π π e − i m ψ [ x + 1 2 x 2 − 1 ( e − i ψ + e i ψ ) ] l d ψ P^m_l(x)=\cfrac{\mathrm i^m}{2\pi}\cfrac{(l+m)!}{l!} \int_{-\pi}^{\pi}e^{-\mathrm imψ} [x+\cfrac{1}{2}\sqrt{x^2-1}(e^{-\mathrm iψ}+e^{\mathrm iψ})]^ldψ Plm​(x)=2πim​l!(l+m)!​∫−ππ​e−imψ[x+21​x2−1 ​(e−iψ+eiψ)]ldψ
或变为拉普拉斯积分 ( x = cos ⁡ θ ) (x=\cosθ) (x=cosθ)
P l m ( x ) = i m 2 π ( l + m ) ! l ! ∫ − π π e − i m ψ [ cos ⁡ θ + i sin ⁡ θ cos ⁡ ψ ] l d ψ (3.6) P^m_l(x)=\cfrac{\mathrm i^m}{2\pi}\cfrac{(l+m)!}{l!} \int_{-\pi}^{\pi}e^{-\mathrm imψ} [\cosθ+\mathrm i\sinθ\cos\mathrm ψ]^ldψ\tag{3.6} Plm​(x)=2πim​l!(l+m)!​∫−ππ​e−imψ[cosθ+isinθcosψ]ldψ(3.6)
连带勒让德多项式的正交性：在区间 ( − 1 , 1 ) (-1,1) (−1,1) 上正交
∫ − 1 1 P l m ( x ) P k m ( x ) d x = 0 ( l ≠ k ) \int_{-1}^{1}P^m_l(x)P^m_k(x)dx=0\quad(l\neq k) ∫−11​Plm​(x)Pkm​(x)dx=0(l​=k)
如果从 x x x 变换回变量 θ ,   x = cos ⁡ θ θ,\ x=\cosθ θ, x=cosθ ，则
∫ 0 π P l m ( cos ⁡ θ ) P k m ( cos ⁡ θ ) sin ⁡ θ d θ = 0 ( l ≠ k ) \int_{0}^{\pi}P^m_l(\cosθ)P^m_k(\cosθ)\sinθdθ=0\quad(l\neq k) ∫0π​Plm​(cosθ)Pkm​(cosθ)sinθdθ=0(l​=k)

连带勒让德多项式的模
∥ P l m ( x ） ∥ 2 = ∫ − 1 1 [ P l m ( x ) ] 2 d x \|P^m_l(x）\|^2=\int_{-1}^{1}[P^m_l(x)]^2dx ∥Plm​(x）∥2=∫−11​[Plm​(x)]2dx
可计算得
∥ P l m ( x ） ∥ = 2 ( l + m ) ! ( 2 l + 1 ) ( l − m ) ! ( l = 0 , 1 , 2 , ⋯   ) (3.7) \|P^m_l(x）\|=\sqrt{\cfrac{2(l+m)!}{(2l+1)(l-m)!}}\quad(l=0,1,2,\cdots)\tag{3.7} ∥Plm​(x）∥=(2l+1)(l−m)!2(l+m)!​ ​(l=0,1,2,⋯)(3.7)

连带傅里叶-勒让德级数：设函数 f ( x ) f(x) f(x) 在区间 [ − 1 , 1 ] [-1,1] [−1,1] 上满足狄利克雷条件，则 f ( x ) f(x) f(x) 在连续点处展开为
f ( x ) = ∑ k = 0 ∞ c k P k m ( x ) f(x)=\sum_{k=0}^{\infty}c_kP^m_k(x) f(x)=k=0∑∞​ck​Pkm​(x)
其中系数
c k = ( 2 l + 1 ) ( l − m ) ! 2 ( l + m ) ! ∫ − 1 1 f ( x ) P k m ( x ) d x c_k=\cfrac{(2l+1)(l-m)!}{2(l+m)!}\int_{-1}^{1}f(x)P^m_k(x)dx ck​=2(l+m)!(2l+1)(l−m)!​∫−11​f(x)Pkm​(x)dx
在物理上常取 x = cos ⁡ θ ( 0 ⩽ θ ⩽ π ) x=\cosθ(0⩽θ⩽\pi) x=cosθ(0⩽θ⩽π) ，则
f ( θ ) = ∑ k = 0 ∞ c k P k m ( cos ⁡ θ ) f(θ)=\sum_{k=0}^{\infty}c_kP^m_k(\cosθ) f(θ)=k=0∑∞​ck​Pkm​(cosθ)
其中系数
c k = ( 2 l + 1 ) ( l − m ) ! 2 ( l + m ) ! ∫ 0 π f ( θ ) P k m ( cos ⁡ θ ) sin ⁡ θ d θ c_k=\cfrac{(2l+1)(l-m)!}{2(l+m)!}\int_{0}^{\pi}f(θ)P^m_k(\cosθ)\sinθdθ ck​=2(l+m)!(2l+1)(l−m)!​∫0π​f(θ)Pkm​(cosθ)sinθdθ

连带勒让德多项式的递推关系
( k − m + 1 ) P k + 1 m ( x ) − ( 2 k + 1 ) x P k m ( x ) + ( k + m ) P k − 1 m ( x ) = 0 (3.8) (k-m+1)P^m_{k+1}(x)-(2k+1)xP^m_k(x)+(k+m)P^m_{k-1}(x)=0\tag{3.8} (k−m+1)Pk+1m​(x)−(2k+1)xPkm​(x)+(k+m)Pk−1m​(x)=0(3.8)

球谐函数

球函数：我们回到拉普拉斯变换在球坐标下的分离变量，我们曾得到方程
1 sin ⁡ θ ∂ ∂ θ ( sin ⁡ θ ∂ S ∂ θ ) + 1 sin ⁡ 2 θ ∂ 2 S ∂ ϕ 2 + μ S = 0 (4.1) \cfrac{1}{\sinθ}\cfrac{∂}{∂θ}\left(\sinθ\cfrac{∂S}{∂θ}\right) +\cfrac{1}{\sin^2θ}\cfrac{∂^2S}{∂ϕ^2}+μS=0\tag{4.1} sinθ1​∂θ∂​(sinθ∂θ∂S​)+sin2θ1​∂ϕ2∂2S​+μS=0(4.1)
称为球函数方程。令 S ( θ , ϕ ) = Θ ( θ ) Φ ( ϕ ) S(θ,ϕ)=Θ(θ)Φ(ϕ) S(θ,ϕ)=Θ(θ)Φ(ϕ) 进一步分离变量，可获得其解
S l m ( θ , ϕ ) = P l m ( cos ⁡ θ ) ( A l m cos ⁡ m ϕ + B l m sin ⁡ m ϕ ) = P l m ( cos ⁡ θ ) { sin ⁡ m ϕ cos ⁡ m ϕ } , ( m = 0 , 1 , 2 , ⋯   , l ) (4.2) \begin{aligned} S_l^m(θ,ϕ) &=P_l^m(\cosθ)(A_l^m\cos mϕ+B_l^m\sin mϕ) \\ &=P_l^m(\cosθ)\begin{Bmatrix} \sin mϕ \\ \cos mϕ \\ \end{Bmatrix}, \end{aligned} \quad (m=0,1,2,\cdots,l)\tag{4.2} Slm​(θ,ϕ)​=Plm​(cosθ)(Alm​cosmϕ+Blm​sinmϕ)=Plm​(cosθ){sinmϕcosmϕ​},​(m=0,1,2,⋯,l)(4.2)
称为 l l l 阶球谐函数 (Spherical harmonics) 。其中常数 μ = l ( l + 1 ) μ=l(l+1) μ=l(l+1) ，符号 { } \{\} {} 表示其中列举的函数是线性独立的，可任取其一。

线性独立的 l l l 阶球函数共有 2 l + 1 2l+1 2l+1 个，这是因为对应于 m = 0 m=0 m=0 ，只有一个球函数 P l ( cos ⁡ θ ) P_l(\cosθ) Pl​(cosθ) ，对应于 m = 1 , 2 , ⋯   , l m=1,2,\cdots,l m=1,2,⋯,l ，则各有两个 P l m ( cos ⁡ θ ) sin ⁡ m ϕ P^m_l(\cosθ)\sin mϕ Plm​(cosθ)sinmϕ 和 P l m ( cos ⁡ θ ) cos ⁡ m ϕ P^m_l(\cosθ)\cos mϕ Plm​(cosθ)cosmϕ。

复数形式的球函数：根据欧拉公式 (4.2) 可以完全写为
S l m ( θ , ϕ ) = P l ∣ m ∣ ( cos ⁡ θ ) e i m ϕ ( m = 0 , ± 1 , ± 2 , ⋯   , ± l ) (4.3) S_l^m(θ,ϕ)=P_l^{|m|}(\cosθ)e^{\mathrm imϕ}\quad (m=0,\pm1,\pm2,\cdots,\pm l) \tag{4.3} Slm​(θ,ϕ)=Pl∣m∣​(cosθ)eimϕ(m=0,±1,±2,⋯,±l)(4.3)
球函数正交关系：任意两个球函数 (4.2) 在球面 S   ( 0 ⩽ θ ⩽ π , 0 ⩽ ϕ ⩽ 2 π ) S\ (0⩽θ⩽\pi,0⩽ϕ⩽2\pi) S (0⩽θ⩽π,0⩽ϕ⩽2π) 上正交
∫ 0 π ∫ 0 2 π S l m ( θ , ϕ ) S k n ( θ , ϕ ) sin ⁡ θ d θ d ϕ = 0 ( m ≠ n  or  l ≠ k ) \int_0^{\pi}\int_0^{2\pi}S_l^m(θ,ϕ)S_k^n(θ,ϕ)\sinθdθdϕ=0\quad(m\neq n\text{ or }l\neq k) ∫0π​∫02π​Slm​(θ,ϕ)Skn​(θ,ϕ)sinθdθdϕ=0(m​=n or l​=k)
球函数的模：
∥ S l m ( θ , ϕ ) ∥ 2 = ∫ 0 π ∫ 0 2 π [ S l m ( θ , ϕ ) ] 2 sin ⁡ θ d θ d ϕ \|S_l^m(θ,ϕ)\|^2=\int_0^{\pi}\int_0^{2\pi}[S_l^m(θ,ϕ)]^2\sinθdθdϕ ∥Slm​(θ,ϕ)∥2=∫0π​∫02π​[Slm​(θ,ϕ)]2sinθdθdϕ
计算得
∥ S l m ( θ , ϕ ) ∥ = 2 π δ m ( l + m ) ! ( 2 l + 1 ) ( l − m ) ! (4.4) \|S_l^m(θ,ϕ)\|=\sqrt{\cfrac{2\piδ_m(l+m)!}{(2l+1)(l-m)!}}\tag{4.4} ∥Slm​(θ,ϕ)∥=(2l+1)(l−m)!2πδm​(l+m)!​ ​(4.4)
其中 δ m = { 2 ( m = 0 ) 1 ( m = 1 , 2 , ⋯   ) δ_m=\begin{cases}2&(m=0) \\ 1 & (m=1,2,\cdots)\end{cases} δm​={21​(m=0)(m=1,2,⋯)​

复数形式的模可写成
∥ S l m ( θ , ϕ ) ∥ = 4 π ( l + ∣ m ∣ ) ! ( 2 l + 1 ) ( l − ∣ m ∣ ) ! (4.5) \|S_l^m(θ,ϕ)\|=\sqrt{\cfrac{4\pi(l+|m|)!}{(2l+1)(l-|m|)!}}\tag{4.5} ∥Slm​(θ,ϕ)∥=(2l+1)(l−∣m∣)!4π(l+∣m∣)!​ ​(4.5)
广义傅里叶级数：定义在球面 S S S 上的函数 f ( θ , ϕ ) f(θ,ϕ) f(θ,ϕ) 以球函数为基的二重傅里叶展开为
f ( θ , ϕ ) = ∑ m = 0 ∞ ∑ l = m ∞ [ A l m cos ⁡ m ϕ + B l m sin ⁡ m ϕ ] P l m ( cos ⁡ θ ) (4.6) f(θ,ϕ)=\sum_{m=0}^{\infty}\sum_{l=m}^{\infty}[A_l^m\cos mϕ+B_l^m\sin mϕ]P_l^m(\cosθ)\tag{4.6} f(θ,ϕ)=m=0∑∞​l=m∑∞​[Alm​cosmϕ+Blm​sinmϕ]Plm​(cosθ)(4.6)
其中系数为
A l m = ( 2 l + 1 ) ( l − m ) ! 2 π δ m ( l + m ) ! ∫ 0 π ∫ 0 2 π f ( θ , ϕ ) P l m ( cos ⁡ θ ) cos ⁡ m ϕ sin ⁡ θ d θ d ϕ A_l^m=\cfrac{(2l+1)(l-m)!}{2\piδ_m(l+m)!} \int_0^{\pi}\int_0^{2\pi}f(θ,ϕ)P_l^m(\cosθ)\cos mϕ\sinθdθdϕ Alm​=2πδm​(l+m)!(2l+1)(l−m)!​∫0π​∫02π​f(θ,ϕ)Plm​(cosθ)cosmϕsinθdθdϕ

B l m = ( 2 l + 1 ) ( l − m ) ! 2 π ( l + m ) ! ∫ 0 π ∫ 0 2 π f ( θ , ϕ ) P l m ( cos ⁡ θ ) sin ⁡ m ϕ sin ⁡ θ d θ d ϕ B_l^m=\cfrac{(2l+1)(l-m)!}{2\pi(l+m)!} \int_0^{\pi}\int_0^{2\pi}f(θ,ϕ)P_l^m(\cosθ)\sin mϕ\sinθdθdϕ Blm​=2π(l+m)!(2l+1)(l−m)!​∫0π​∫02π​f(θ,ϕ)Plm​(cosθ)sinmϕsinθdθdϕ

复数形式的傅里叶展开为
f ( θ , ϕ ) = ∑ l = 0 ∞ ∑ m = − l l C l m P l ∣ m ∣ ( cos ⁡ θ ) e i m ϕ (4.7) f(θ,ϕ)=\sum_{l=0}^{\infty}\sum_{m=-l}^{l}C_l^mP_l^{|m|}(\cosθ)e^{\mathrm imϕ}\tag{4.7} f(θ,ϕ)=l=0∑∞​m=−l∑l​Clm​Pl∣m∣​(cosθ)eimϕ(4.7)
其中系数为
C l m = ( 2 l + 1 ) ( l − ∣ m ∣ ) ! 4 π ( l + ∣ m ∣ ) ! ∫ 0 π ∫ 0 2 π f ( θ , ϕ ) P l ∣ m ∣ ( cos ⁡ θ ) [ e i m ϕ ] ∗ sin ⁡ θ d θ d ϕ C_l^m=\cfrac{(2l+1)(l-|m|)!}{4\pi(l+|m|)!} \int_0^{\pi}\int_0^{2\pi}f(θ,ϕ)P_l^{|m|}(\cosθ)[e^{\mathrm imϕ}]^*\sinθdθdϕ Clm​=4π(l+∣m∣)!(2l+1)(l−∣m∣)!​∫0π​∫02π​f(θ,ϕ)Pl∣m∣​(cosθ)[eimϕ]∗sinθdθdϕ
其中 [ e i m ϕ ] ∗ [e^{\mathrm imϕ}]^* [eimϕ]∗ 是 e i m ϕ e^{\mathrm imϕ} eimϕ 的共轭复数。

正交归一化：物理中常常用正交归一化的球函数
Y l m = ( 2 l + 1 ) ( l − ∣ m ∣ ) ! 4 π ( l + ∣ m ∣ ) ! P l ∣ m ∣ ( cos ⁡ θ ) e i m ϕ ( m = 0 , ± 1 , ± 2 , ⋯   , ± l ) (4.8) Y_l^m=\sqrt{\cfrac{(2l+1)(l-|m|)!}{4\pi(l+|m|)!}} P_l^{|m|}(\cosθ)e^{\mathrm imϕ}\quad (m=0,\pm1,\pm2,\cdots,\pm l) \tag{4.8} Ylm​=4π(l+∣m∣)!(2l+1)(l−∣m∣)!​ ​Pl∣m∣​(cosθ)eimϕ(m=0,±1,±2,⋯,±l)(4.8)
这时就有正交归一关系
∫ 0 π ∫ 0 2 π Y l m ( θ , ϕ ) Y k n ( θ , ϕ ) sin ⁡ θ d θ d ϕ = δ l , k δ m , n \int_0^{\pi}\int_0^{2\pi}Y_l^m(θ,ϕ)Y_k^n(θ,ϕ)\sinθdθdϕ=δ_{l,k}δ_{m,n} ∫0π​∫02π​Ylm​(θ,ϕ)Ykn​(θ,ϕ)sinθdθdϕ=δl,k​δm,n​

柱函数

贝塞尔方程的解

贝塞尔方程(Bessel equation)
x 2 y ′ ′ + x y ′ + ( x 2 − ν 2 ) y = 0 (1.1) x^2y''+xy'+(x^2-ν^2)y=0\tag{1.1} x2y′′+xy′+(x2−ν2)y=0(1.1)

其中 ν ν ν 为实参数。由于方程是二阶变系数常微分方程，采用幂级数求解，设其解的形式为
y = ∑ k = 0 ∞ c k x k + r (1.2) y=\displaystyle\sum_{k=0}^∞c_kx^{k+r}\tag{1.2} y=k=0∑∞​ck​xk+r(1.2)

其中 c 0 ≠ 0 , c k , r c_0\neq0,\quad c_k,r c0​​=0,ck​,r 是待定常数。带入贝塞尔方程可得
x 2 ∑ k = 1 ∞ ( k + r ) ( k + r − 1 ) c k x k + r − 2 + x ∑ k = 1 ∞ ( k + r ) c k x k + r − 1 + ( x 2 − ν 2 ) ∑ k = 0 ∞ ( k + r ) c k x k + r = 0 \displaystyle x^2\sum_{k=1}^∞(k+r)(k+r-1)c_kx^{k+r-2} +x\sum_{k=1}^∞(k+r)c_kx^{k+r-1} +(x^2-ν^2)\sum_{k=0}^∞(k+r)c_kx^{k+r}=0 x2k=1∑∞​(k+r)(k+r−1)ck​xk+r−2+xk=1∑∞​(k+r)ck​xk+r−1+(x2−ν2)k=0∑∞​(k+r)ck​xk+r=0
进一步合并 x x x 的同幂项
∑ k = 0 ∞ [ ( k + r ) ( k + r − 1 ) + ( k + r ) − ν 2 ] c k x k + r + ∑ k = 0 ∞ c k x k + r + 2 = 0 \displaystyle\sum_{k=0}^∞[(k+r)(k+r-1)+(k+r)-ν^2]c_kx^{k+r}+\sum_{k=0}^∞c_kx^{k+r+2}=0 k=0∑∞​[(k+r)(k+r−1)+(k+r)−ν2]ck​xk+r+k=0∑∞​ck​xk+r+2=0
令各项的系数等于零，得代数方程组
{ c 0 [ r 2 − ν 2 ] = 0 c 1 [ ( r + 1 ) 2 − ν 2 ] = 0 ⋯ ⋯ c k [ ( r + k ) 2 − ν 2 ] + c k − 2 = 0 ⋯ ⋯ \begin{cases} c_0[r^2-ν^2]=0 \\ c_1[(r+1)^2-ν^2]=0 \\ \cdots\quad\cdots \\ c_k[(r+k)^2-ν^2]+c_{k-2}=0 \\ \cdots\quad\cdots \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​c0​[r2−ν2]=0c1​[(r+1)2−ν2]=0⋯⋯ck​[(r+k)2−ν2]+ck−2​=0⋯⋯​
因为 c 0 ≠ 0 c_0\neq0 c0​​=0 ，故从方程组解得 r = ± ν r=\pm ν r=±ν
(1) 当 r = ν r= ν r=ν 时，带入代数方程组可得
c 1 = 0 , c k = − c k − 2 k ( 2 ν + k ) ( k = 2 , 3 , ⋯   ) c_1=0,\quad c_k=-\cfrac{c_{k-2}}{k(2ν+k)}\quad (k=2,3,\cdots) c1​=0,ck​=−k(2ν+k)ck−2​​(k=2,3,⋯)
或按下标是奇数或偶数，我们分别有
{ c 2 k + 1 = − c 2 k − 1 ( 2 k + 1 ) ( 2 ν + 2 k + 1 ) c 2 k = − c 2 k − 2 2 k ( 2 ν + 2 k ) ( k = 1 , 2 , ⋯   ) \begin{cases} c_{2k+1}=\cfrac{-c_{2k-1}}{(2k+1)(2ν+2k+1)} \\ c_{2k}=\cfrac{-c_{2k-2}}{2k(2ν+2k)} \end{cases}\quad (k=1,2,\cdots) ⎩⎪⎪⎨⎪⎪⎧​c2k+1​=(2k+1)(2ν+2k+1)−c2k−1​​c2k​=2k(2ν+2k)−c2k−2​​​(k=1,2,⋯)
从而求得
{ c 2 k − 1 = 0 c 2 k = ( − 1 ) k c 0 2 2 k k ! ( ν + 1 ) ( ν + 2 ) ⋯ ( ν + k ) ( k = 1 , 2 , ⋯   ) \begin{cases} c_{2k-1}=0 \\ c_{2k}=(-1)^k\cfrac{c_0}{2^{2k}k!(ν+1)(ν+2)\cdots(ν+k)} \\ \end{cases}\quad (k=1,2,\cdots) ⎩⎨⎧​c2k−1​=0c2k​=(−1)k22kk!(ν+1)(ν+2)⋯(ν+k)c0​​​(k=1,2,⋯)
将各 c k c_k ck​ 带入 (1.2) 得到贝塞尔方程得一个解
y 1 = c 0 x ν + ∑ k = 1 ∞ ( − 1 ) k c 0 2 2 k k ! ( ν + 1 ) ( ν + 2 ) ⋯ ( ν + k ) x 2 k + ν \displaystyle y_1=c_0x^ν+\sum_{k=1}^{∞}(-1)^k\cfrac{c_0}{2^{2k}k!(ν+1)(ν+2)\cdots(ν+k)}x^{2k+ν} y1​=c0​xν+k=1∑∞​(−1)k22kk!(ν+1)(ν+2)⋯(ν+k)c0​​x2k+ν
此时 c 0 c_0 c0​ 仍是任意常数，通常为求特解取
c 0 = 1 2 ν Γ ( ν + 1 ) c_0=\cfrac{1}{2^ν\Gamma(ν+1)} c0​=2νΓ(ν+1)1​ ，其中² Γ ( s ) = ∫ 0 ∞ x s − 1 e − x d x \displaystyle\Gamma(s)=\int_{0}^{∞}x^{s-1}e^{-x}dx Γ(s)=∫0∞​xs−1e−xdx
从而上式特解变为
J ν ( x ) = ∑ k = 0 ∞ ( − 1 ) k k ! Γ ( ν + k + 1 ) ( x 2 ) 2 k + ν (1.3) \displaystyle J_ν(x)=\sum_{k=0}^{∞}\cfrac{(-1)^k}{k!\Gamma(ν+k+1)}(\cfrac{x}{2})^{2k+ν}\tag{1.3} Jν​(x)=k=0∑∞​k!Γ(ν+k+1)(−1)k​(2x​)2k+ν(1.3)

J ν ( x ) J_ν(x) Jν​(x) 是由贝塞尔方程定义得特殊函数，称为 ν ν ν 阶第一类贝塞尔函数。
由达朗贝尔判别法不难验证级数 J ν ( x ) J_ν(x) Jν​(x) 在 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 收敛，因此，贝塞尔方程总有一个特解 J ν ( x ) J_ν(x) Jν​(x)，我们只需寻求另一个线性无关的特解即可求得贝塞尔方程通解。

(2) 当 r = − ν r=-ν r=−ν 时，和 r = ν r=ν r=ν 的求解过程一样，我们可以求得另一个特解
y 2 = c 0 x − ν + ∑ k = 1 ∞ ( − 1 ) k c 0 2 2 k k ! ( − ν + 1 ) ( − ν + 2 ) ⋯ ( − ν + k ) x 2 k − ν \displaystyle y_2=c_0x^{-ν}+\sum_{k=1}^{∞}(-1)^k\cfrac{c_0}{2^{2k}k!(-ν+1)(-ν+2)\cdots(-ν+k)}x^{2k-ν} y2​=c0​x−ν+k=1∑∞​(−1)k22kk!(−ν+1)(−ν+2)⋯(−ν+k)c0​​x2k−ν
此时，令 c 0 = 1 2 − ν Γ ( − ν + 1 ) c_0=\cfrac{1}{2^{-ν}\Gamma(-ν+1)} c0​=2−νΓ(−ν+1)1​ ，从而上式特解变为
J − ν ( x ) = ∑ k = 0 ∞ ( − 1 ) k k ! Γ ( − ν + k + 1 ) ( x 2 ) 2 k − ν (1.4) \displaystyle J_{-ν}(x)=\sum_{k=0}^{∞}\cfrac{(-1)^k}{k!\Gamma(-ν+k+1)}(\cfrac{x}{2})^{2k-ν}\tag{1.4} J−ν​(x)=k=0∑∞​k!Γ(−ν+k+1)(−1)k​(2x​)2k−ν(1.4)

级数 J − ν ( x ) J_{-ν}(x) J−ν​(x) 在 x > 0 x>0 x>0 时收敛。由于当 ν ν ν 不为整数时 J ν ( x ) J_{ν}(x) Jν​(x) 和 J − ν ( x ) J_{-ν}(x) J−ν​(x) 线性无关，贝塞尔方程的通解为
y = C 1 J ν ( x ) + C 2 J − ν ( x ) (1.5) y=C_1J_ν(x)+C_2J_{-ν}(x) \tag{1.5} y=C1​Jν​(x)+C2​J−ν​(x)(1.5)
其中 C 1 , C 2 C_1,C_2 C1​,C2​ 为任意常数。
有时取 C 1 = cot ⁡ ν π , C 2 = − csc ⁡ ν π C_1=\cot ν\pi,\quad C_2=-\csc ν\pi C1​=cotνπ,C2​=−cscνπ 带入 (1.5) 得到一个特解，作为 J ν ( x ) J_ν(x) Jν​(x) 另一个线性无关的特解
N ν ( x ) = J ν ( x ) cos ⁡ ν π − J − ν ( x ) sin ⁡ ν π (1.6) N_ν(x)=\cfrac{J_ν(x)\cos ν\pi-J_{-ν}(x)}{\sin ν\pi}\tag{1.6} Nν​(x)=sinνπJν​(x)cosνπ−J−ν​(x)​(1.6)
叫做 ν ν ν 阶诺依曼函数 (Neumann)或 ν ν ν 阶第二类贝塞尔函数。因此贝塞尔方程的通解也可取为
y = C 1 J ν ( x ) + C 2 N ν ( x ) (1.7) y=C_1J_ν(x)+C_2N_ν(x)\tag{1.7} y=C1​Jν​(x)+C2​Nν​(x)(1.7)
(3) 当 ν = n ν=n ν=n 为正整数时， J − n ( x ) = ( − 1 ) n J n ( x ) J_{-n}(x)=(-1)^nJ_n(x) J−n​(x)=(−1)nJn​(x) 与 J n ( x ) J_n(x) Jn​(x) 线性相关。我们可以考虑诺依曼函数，定义
Y n ( x ) = lim ⁡ α → n J α ( x ) cos ⁡ ν π − J − α ( x ) sin ⁡ α π Y_n(x)=\lim\limits_{α\to n}\cfrac{J_α(x)\cos ν\pi-J_{-α}(x)}{\sin α\pi} Yn​(x)=α→nlim​sinαπJα​(x)cosνπ−J−α​(x)​
上式为 0 0 \frac{0}{0} 00​ 不定式，根据洛必达法则得
Y n ( x ) = lim ⁡ α → n ( ∂ J α ( x ) ∂ α − 1 cos ⁡ α π ∂ J − α ( x ) ∂ α ) Y_n(x)=\lim\limits_{α\to n}(\cfrac{∂J_α(x)}{∂α}-\cfrac{1}{\cosα\pi}\cfrac{∂J_{-α}(x)}{∂α}) Yn​(x)=α→nlim​(∂α∂Jα​(x)​−cosαπ1​∂α∂J−α​(x)​)
可以证明 J n ( x ) , Y n ( x ) J_n(x),Y_n(x) Jn​(x),Yn​(x) 线性无关，因此对于任意实数 ν ν ν ，贝塞尔方程的通解为
y = C 1 J ν ( x ) + C 2 Y ν ( x ) (1.8) y=C_1J_ν(x)+C_2Y_ν(x)\tag{1.8} y=C1​Jν​(x)+C2​Yν​(x)(1.8)
虚宗量贝塞尔方程
x 2 y ′ ′ + x y ′ − ( x 2 + ν 2 ) y = 0 (1.9) x^2y''+xy'-(x^2+ν^2)y=0\tag{1.9} x2y′′+xy′−(x2+ν2)y=0(1.9)
做变量变换 t = i x t=\mathrm{i}x t=ix ，方程变为 t 2 y ′ ′ + t y ′ + ( t 2 − ν 2 ) y = 0 t^2y''+ty'+(t^2-ν^2)y=0 t2y′′+ty′+(t2−ν2)y=0 已求得其解。
(1) 当 ν ν ν 非整数时，通常取一般解为
y = C 1 I ν ( x ) + C 2 I − ν ( x ) (1.10) y=C_1I_ν(x)+C_2I_{-ν}(x)\tag{1.10} y=C1​Iν​(x)+C2​I−ν​(x)(1.10)
其中 I ν ( x ) = i − ν J ν ( i x ) , I − ν ( x ) = i ν J − ν ( i x ) I_ν(x)=\mathrm{i}^{-ν}J_ν(\mathrm{i}x),I_{-ν}(x)=\mathrm{i}^{ν}J_{-ν}(\mathrm{i}x) Iν​(x)=i−νJν​(ix),I−ν​(x)=iνJ−ν​(ix) 为实值函数，称为虚宗量贝塞尔函数。
(2) 关于第二类虚宗量贝塞尔函数的处理，通常又取线性独立的特解
{ H ν ( 1 ) ( x ) = J ν ( x ) + i N ν ( x ) H ν ( 2 ) ( x ) = J ν ( x ) − i N ν ( x ) \begin{cases} H_ν^{(1)}(x)=J_ν(x)+\mathrm{i}N_ν(x) \\ H_ν^{(2)}(x)=J_ν(x)-\mathrm{i}N_ν(x) \end{cases} {Hν(1)​(x)=Jν​(x)+iNν​(x)Hν(2)​(x)=Jν​(x)−iNν​(x)​
并称为第一种和第二种汉克儿函数 (Hankel)，或第三类贝塞尔函数。于是虚宗量贝塞尔方程的一般解又可表示为
y = C 1 H ν ( 1 ) ( x ) + C 2 H ν ( 2 ) ( x ) y=C_1H_ν^{(1)}(x)+C_2H_ν^{(2)}(x) y=C1​Hν(1)​(x)+C2​Hν(2)​(x)
为了获得两个线性独立的实数特解通常：
当 ν ν ν 非整数时，取
K ν ( x ) = π 2 i exp ⁡ ( i π ν 2 ) H ν ( 1 ) ( i x ) = π 2 sin ⁡ ν π [ I − ν ( x ) − I ν ( x ) ] K_ν(x)=\cfrac{\pi}{2}\mathrm{i}\exp(\cfrac{\mathrm{i}\pi ν}{2})H_ν^{(1)}(\mathrm{i}x) =\cfrac{\pi}{2\sinν\pi}[I_{-ν}(x)-I_ν(x)] Kν​(x)=2π​iexp(2iπν​)Hν(1)​(ix)=2sinνππ​[I−ν​(x)−Iν​(x)]
当 ν = n ν= n ν=n 是整数时，取极限
K ν ( x ) = lim ⁡ α → ν π 2 sin ⁡ α π [ I − α ( x ) − I α ( x ) ] K_ν(x)=\lim\limits_{α\to ν}\cfrac{\pi}{2\sinα\pi}[I_{-α}(x)-I_α(x)] Kν​(x)=α→νlim​2sinαππ​[I−α​(x)−Iα​(x)]
函数 K ν ( x ) K_ν(x) Kν​(x) 称为虚宗量汉克尔函数 。通常取虚宗量贝塞尔方程的解为
y = C 1 I ν ( x ) + C 2 K ν ( x ) (1.11) y=C_1I_ν(x)+C_2K_{ν}(x)\tag{1.11} y=C1​Iν​(x)+C2​Kν​(x)(1.11)

贝塞尔函数

整数阶贝塞尔函数的性质 ：第二、三类贝塞尔函数都是第一类贝塞尔函数的线性组合，因此第一类贝塞尔函数的性质都适用。

(1) J n ( x ) J_{n}(x) Jn​(x) 与 J − n ( x ) J_{-n}(x) J−n​(x) 线性相关
J − n ( x ) = ( − 1 ) n J n ( x ) J_{-n}(x)=(-1)^nJ_n(x) J−n​(x)=(−1)nJn​(x)
(2) J n ( x ) J_n(x) Jn​(x) 的奇偶性
J n ( − x ) = ( − 1 ) n J n ( x ) J_n(-x)=(-1)^nJ_n(x) Jn​(−x)=(−1)nJn​(x)
(3) J n ( x ) J_n(x) Jn​(x) 的生成函数
exp ⁡ [ x 2 ( t − 1 t ) ] = ∑ n = − ∞ + ∞ J n ( x ) t n ( n ≠ 0 ) \displaystyle\exp[\cfrac{x}{2}(t-\cfrac{1}{t})] =\sum_{n=-\infty}^{+\infty}J_n(x)t^n\quad (n\neq0) exp[2x​(t−t1​)]=n=−∞∑+∞​Jn​(x)tn(n​=0)
(4) J n ( x ) J_n(x) Jn​(x) 的积分表示：生成函数中令 t = e i θ t=e^{\mathrm iθ} t=eiθ 得到
J n ( x ) = 1 π ∫ 0 π cos ⁡ ( x sin ⁡ θ − n θ ) d θ J_n(x)=\cfrac{1}{\pi}\int_0^\pi\cos(x\sinθ-nθ)dθ Jn​(x)=π1​∫0π​cos(xsinθ−nθ)dθ
(5) 如果生成函数中令 t = i e i θ t=\mathrm ie^{\mathrm iθ} t=ieiθ 得到
e i k r cos ⁡ θ = J 0 ( k r ) + 2 ∑ n = 1 ∞ i n J n ( k r ) cos ⁡ n θ e^{\mathrm ikr\cosθ}=J_0(kr)+2\displaystyle\sum_{n=1}^{\infty}\mathrm i^nJ_n(kr)\cos nθ eikrcosθ=J0​(kr)+2n=1∑∞​inJn​(kr)cosnθ
ν ν ν 阶贝塞尔函数的性质

(1) 递推关系式
d d x [ x ν J ν ( x ) ] = x ν J ν − 1 ( x ) d d x [ x − ν J ν ( x ) ] = − x − ν J ν + 1 ( x ) (2.1) \cfrac{d}{dx}[x^νJ_ν(x)]=x^νJ_{ν-1}(x) \\ \cfrac{d}{dx}[x^{-ν}J_ν(x)]=-x^{-ν}J_{ν+1}(x) \tag{2.1} dxd​[xνJν​(x)]=xνJν−1​(x)dxd​[x−νJν​(x)]=−x−νJν+1​(x)(2.1)
从递推关系式中还可以得到两个新的关系式
J ν − 1 ( x ) − J ν + 1 ( x ) = 2 J ν ′ ( x ) J ν − 1 ( x ) + J ν + 1 ( x ) = 2 ν x J ν ( x ) J_{ν-1}(x)-J_{ν+1}(x)=2J'_{ν}(x) \\ J_{ν-1}(x)+J_{ν+1}(x)=\cfrac{2ν}{x}J_{ν}(x) Jν−1​(x)−Jν+1​(x)=2Jν′​(x)Jν−1​(x)+Jν+1​(x)=x2ν​Jν​(x)
(2) 贝塞尔函数 J ν ( x ) J_{ν}(x) Jν​(x) 与 J − ν ( x ) J_{-ν}(x) J−ν​(x) 的 Wronski 行列式
W [ J ν ( x ) , J − ν ( x ) ] = ∣ J ν ( x ) J − ν ( x ) J ν ′ ( x ) J − ν ′ ( x ) ∣ = − 2 π x sin ⁡ π ν (2.2) W[J_{ν}(x),J_{-ν}(x)]=\begin{vmatrix} J_{ν}(x) & J_{-ν}(x) \\ J'_{ν}(x) & J'_{-ν}(x) \end{vmatrix}=-\cfrac{2}{\pi x}\sin\piν\tag{2.2} W[Jν​(x),J−ν​(x)]=∣∣∣∣​Jν​(x)Jν′​(x)​J−ν​(x)J−ν′​(x)​∣∣∣∣​=−πx2​sinπν(2.2)
半奇数阶贝塞尔函数：第一类贝塞尔函数和诺依曼函数一般不是初等函数，但半奇数阶第一类贝塞尔函数 J n + 1 2 ( x ) ( n = 0 , 1 , 2 , ⋯   ) J_{n+\frac{1}{2}}(x)\quad (n=0,1,2,\cdots) Jn+21​​(x)(n=0,1,2,⋯) 可以用初等函数表示，由递推关系可得
J 1 2 ( x ) = 2 π x sin ⁡ x , J − 1 2 ( x ) = 2 π x cos ⁡ x J_{\frac{1}{2}}(x)=\sqrt{\cfrac{2}{\pi x}}\sin x,\quad J_{-\frac{1}{2}}(x)=\sqrt{\cfrac{2}{\pi x}}\cos x J21​​(x)=πx2​ ​sinx,J−21​​(x)=πx2​ ​cosx

J n + 1 2 ( x ) = ( − 1 ) n 2 π x x n ( d x d x ) n ( sin ⁡ x x ) J − ( n + 1 2 ) ( x ) = 2 π x x n ( d x d x ) n ( cos ⁡ x x ) (2.3) J_{n+\frac{1}{2}}(x)=(-1)^n\sqrt{\cfrac{2}{\pi x}}x^n (\cfrac{d}{xdx})^n(\cfrac{\sin x}{x}) \\ J_{-(n+\frac{1}{2})}(x)=\sqrt{\cfrac{2}{\pi x}}x^n (\cfrac{d}{xdx})^n(\cfrac{\cos x}{x}) \tag{2.3} Jn+21​​(x)=(−1)nπx2​ ​xn(xdxd​)n(xsinx​)J−(n+21​)​(x)=πx2​ ​xn(xdxd​)n(xcosx​)(2.3)
贝塞尔函数的零点：即方程 J ν ( x ) = 0 J_{ν}(x)=0 Jν​(x)=0 的根，在求解数学物理方程定解问题时，具有重要意义。 由级数表达式 (1.3) 知 J ν ( x ) J_{ν}(x) Jν​(x) 为偶函数，故实数零点存在的话，必然成对出现，而 J 0 ( 0 ) = 1 , J ν ( 0 ) = 0 ( ν > 0 ) J_0(0)=1,J_ν(0)=0(ν>0) J0​(0)=1,Jν​(0)=0(ν>0) 。下面给出一些结论：
(1) J ν ( x ) J_{ν}(x) Jν​(x) 由无穷多个单重零点，且在实轴上关于原点对称分布，因而必有无穷多个正零点。当 ν > − 1 ν>-1 ν>−1 或为整数时，只有实数零点。
(2) J ν ( x ) J_{ν}(x) Jν​(x) 的零点和 J ν + 1 ( x ) J_{ν+1}(x) Jν+1​(x) 的零点彼此相间，且没有非零的公共零点。
(3) 设 μ 1 < μ 2 < ⋯ < μ m < μ m + 1 < ⋯ μ_1<μ_2<\cdots<μ_m<μ_{m+1}<\cdots μ1​<μ2​<⋯<μm​<μm+1​<⋯ 表示 J ν ( x ) J_{ν}(x) Jν​(x)的正实零点，则当 m → ∞ m\to\infty m→∞ 时， μ m + 1 − μ m → π μ_{m+1}-μ_{m}\to\pi μm+1​−μm​→π ，即 J ν ( x ) J_{ν}(x) Jν​(x) 几乎是以 2 π 2\pi 2π 为周期的周期函数。
(4) 第二类贝塞尔函数 Y ν ( x ) Y_ν(x) Yν​(x) 的零点分布在 ( 0 , + ∞ ) (0,+\infty) (0,+∞) 上，他与第一类贝塞尔函数零点有相似的结论。
(5) 虚宗量贝塞尔函数 I ν ( x ) I_ν(x) Iν​(x) 和虚宗量贝塞尔函数 K ν ( x ) K_ν(x) Kν​(x) 不存在实数零点。

贝塞尔函数的渐进展开：一般用于判断自然边界条件进行取舍
(1) 当 x → 0 x\to0 x→0 时， J 0 ( x ) → 1 , J ν ( x ) → 0 , J − ν ( x ) → ∞ N 0 ( x ) → − ∞ , N ν ( x ) → ± ∞ ( ν ≠ 0 ) J_0(x)\to1,\quad J_ν(x)\to0,\quad J_{-ν}(x)\to\infty \\ N_0(x)\to-\infty,\quad N_ν(x)\to\pm\infty\quad(ν\neq0) J0​(x)→1,Jν​(x)→0,J−ν​(x)→∞N0​(x)→−∞,Nν​(x)→±∞(ν​=0)
(2) 当 x → ∞ x\to\infty x→∞ 时， H ν ( 1 ) ( x ) ∼ 2 π x exp ⁡ [ i ( x − ν π 2 − π 4 ) ] H ν ( 2 ) ( x ) ∼ 2 π x exp ⁡ [ − i ( x − ν π 2 − π 4 ) ] J ν ( x ) ∼ 2 π x cos ⁡ ( x − ν π 2 − π 4 ) N ν ( x ) ∼ 2 π x sin ⁡ ( x − ν π 2 − π 4 ) H_ν^{(1)}(x)\sim\sqrt{\cfrac{2}{\pi x}}\exp[\mathrm i(x-\cfrac{ν\pi}{2}-\cfrac{\pi}{4})] \\ H_ν^{(2)}(x)\sim\sqrt{\cfrac{2}{\pi x}}\exp[-\mathrm i(x-\cfrac{ν\pi}{2}-\cfrac{\pi}{4})] \\ J_ν(x)\sim\sqrt{\cfrac{2}{\pi x}}\cos(x-\cfrac{ν\pi}{2}-\cfrac{\pi}{4}) \\ N_ν(x)\sim\sqrt{\cfrac{2}{\pi x}}\sin(x-\cfrac{ν\pi}{2}-\cfrac{\pi}{4}) Hν(1)​(x)∼πx2​ ​exp[i(x−2νπ​−4π​)]Hν(2)​(x)∼πx2​ ​exp[−i(x−2νπ​−4π​)]Jν​(x)∼πx2​ ​cos(x−2νπ​−4π​)Nν​(x)∼πx2​ ​sin(x−2νπ​−4π​)

贝塞尔函数与本征值问题：以三维空间拉普拉斯方程圆柱坐标系分离变量法为例
在圆柱内 ( 0 ⩽ r ⩽ r 0 ) (0⩽r⩽r_0) (0⩽r⩽r0​) 关于半径 r r r 的微分方程
R ′ ′ + 1 r R ′ − ( μ + m 2 r 2 ) R = 0 ( m = 0 , 1 , 2 , ⋯   ) R''+\cfrac{1}{r}R'-(μ+\cfrac{m^2}{r^2})R=0\quad(m=0,1,2,\cdots) R′′+r1​R′−(μ+r2m2​)R=0(m=0,1,2,⋯)
分三种情况讨论，如果有柱侧边界条件的限制，当 μ > 0 μ>0 μ>0 时，得到虚宗量贝塞尔方程，不存在实数零点，应予排除。
当 μ ⩽ 0 μ⩽0 μ⩽0 取 μ = − ν 2 , x = ν r μ=−ν^2, x=νr μ=−ν2,x=νr 得到整数 m m m 阶贝塞尔方程 (Bessel)
x 2 d 2 R d x 2 + x d R d x + ( x 2 − m 2 ) R = 0 x^2\cfrac{d^2R}{dx^2}+x\cfrac{dR}{dx}+(x^2-m^2)R=0 x2dx2d2R​+xdxdR​+(x2−m2)R=0
在这个方程的线性独立解中，由于自然边界条件的限制 m ⩾ 0 m ⩾ 0 m⩾0 ，我们只要非负阶贝塞尔函数
R ( r ) = J m ( x ) = J m ( − μ r ) R(r)=J_m(x)=J_m(\sqrt{-μ}r) R(r)=Jm​(x)=Jm​(−μ ​r)
再由圆柱侧面的齐次边界条件决定本征值 μ μ μ ，和相应的本征函数 R ( r ) R(r) R(r) 。
对于第一类齐次边界条件 R ( r 0 ) = 0 R(r_0)=0 R(r0​)=0 ，即 J m ( − μ r 0 ) = 0 J_m(\sqrt{-μ}r_0)=0 Jm​(−μ ​r0​)=0
对于第二类齐次边界条件 R ′ ( r 0 ) = 0 R'(r_0)=0 R′(r0​)=0 ，即 − μ J m ′ ( − μ r 0 ) = 0 \sqrt{-μ}J'_m(\sqrt{-μ}r_0)=0 −μ ​Jm′​(−μ ​r0​)=0 ，若 μ ≠ 0 \mu\neq0 μ​=0 ，则 J m ′ ( − μ r 0 ) = 0 J'_m(\sqrt{-μ}r_0)=0 Jm′​(−μ ​r0​)=0
对于第三类齐次边界条件 R ( r 0 ) + H R ′ ( r 0 ) = 0 R(r_0)+HR'(r_0)=0 R(r0​)+HR′(r0​)=0 ，即 J m ( − μ r 0 ) + H − μ J m ′ ( − μ r 0 ) = 0 J_m(\sqrt{-μ}r_0)+H\sqrt{-μ}J'_m(\sqrt{-μ}r_0)=0 Jm​(−μ ​r0​)+H−μ ​Jm′​(−μ ​r0​)=0 。

贝塞尔函数的正交性：作为施图姆-刘维尔本征值问题正交关系的特例，用 μ k μ_k μk​ 表示 J m ( μ r ) J_m(\sqrt{μ}r) Jm​(μ ​r) 在圆柱侧面常见的三类齐次边界条件的第 k k k 个正根或本征值，在区间 [ 0 , r 0 ] [0,r_0] [0,r0​] 上带权重函数 r r r 正交
∫ 0 r 0 J m ( μ k r ) J m ( μ l r ) r d r = 0 ( k ≠ l ) \displaystyle\int_{0}^{r_0}J_m(\sqrt{μ_k}r)J_m(\sqrt{μ_l}r)rdr=0\quad(k\neq l) ∫0r0​​Jm​(μk​ ​r)Jm​(μl​ ​r)rdr=0(k​=l)
贝塞尔函数的模：为了用于计算基于贝塞尔函数的广义傅里叶展开，定义模
∥ J m ( μ k r ) ∥ 2 = ∫ 0 r 0 J m 2 ( μ k r ) r d r = 1 2 ( r 0 2 − m 2 μ k ) J m 2 ( μ k r 0 ) + 1 2 r 0 2 [ J m ′ ( μ k r 0 ) ] 2 (2.4) \begin{aligned} \|J_m(\sqrt{μ_k}r)\|^2 &=\int_{0}^{r_0}J^2_m(\sqrt{μ_k}r)rdr \\ &=\cfrac{1}{2}(r_0^2-\cfrac{m^2}{μ_k})J^2_{m}(\sqrt{μ_k}r_0) +\cfrac{1}{2}r_0^2[J'_{m}(\sqrt{μ_k}r_0)]^2 \end{aligned}\tag{2.4} ∥Jm​(μk​ ​r)∥2​=∫0r0​​Jm2​(μk​ ​r)rdr=21​(r02​−μk​m2​)Jm2​(μk​ ​r0​)+21​r02​[Jm′​(μk​ ​r0​)]2​(2.4)
傅里叶-贝塞尔级数：设函数 f ( r ) f(r) f(r) 在区间 [ 0 , r 0 ] [0,r_0] [0,r0​] 上满足狄利克雷条件，且 f ( 0 ) f(0) f(0) 有界， f ( r 0 ) = 0 f(r_0)=0 f(r0​)=0 则函数 f ( r ) f(r) f(r) 的傅里叶-贝塞尔级数是
f ( r ) = ∑ k = 1 ∞ c k J m ( μ k r ) (2.5) \displaystyle f(r)=\sum_{k=1}^{\infty}c_kJ_m(\sqrt{μ_k}r)\tag{2.5} f(r)=k=1∑∞​ck​Jm​(μk​ ​r)(2.5)
其中系数
c k = 1 ∥ J m ( μ k r ) ∥ 2 ∫ 0 r 0 f ( r ) J m ( μ k r ) r d r (2.6) c_k=\cfrac{1}{\|J_m(\sqrt{μ_k}r)\|^2}\int_0^{r_0}f(r)J_m(\sqrt{μ_k}r)rdr\tag{2.6} ck​=∥Jm​(μk​ ​r)∥21​∫0r0​​f(r)Jm​(μk​ ​r)rdr(2.6)
当 r 0 → ∞ r_0\to\infty r0​→∞ 时，则有傅里叶-贝塞尔积分
f ( r ) = ∫ 0 ∞ F ( ω ) J m ( ω r ) ω d ω F ( ω ) = ∫ 0 ∞ f ( r ) J m ( ω r ) r d r f(r)=\int_0^{\infty}F(ω)J_m(ωr)ωdω \\ F(ω)=\int_0^{\infty}f(r)J_m(ωr)rdr f(r)=∫0∞​F(ω)Jm​(ωr)ωdωF(ω)=∫0∞​f(r)Jm​(ωr)rdr

球贝塞尔方程

d d r ( r 2 d R d r ) + [ k 2 r 2 − l ( l + 1 ) ] R = 0 (3.1) \cfrac{d}{dr}\left(r^2\cfrac{dR}{dr}\right)+[k^2r^2-l(l+1)]R=0\tag{3.1} drd​(r2drdR​)+[k2r2−l(l+1)]R=0(3.1)

做变量变换 x = k r , R ( r ) = π 2 x y ( x ) x=kr,\quad R(r)=\sqrt{\cfrac{\pi}{2x}}y(x) x=kr,R(r)=2xπ​ ​y(x) 带入上式，则方程化为 l + 1 / 2 l+1/2 l+1/2 阶贝塞尔方程
x 2 y ′ ′ + x y ′ + [ x 2 − ( l + 1 2 ) 2 ] y = 0 (3.2) x^2y''+xy'+[x^2-(l+\cfrac{1}{2})^2]y=0\tag{3.2} x2y′′+xy′+[x2−(l+21​)2]y=0(3.2)
若 k = 0 k=0 k=0 ，方程 (3.1) 退化为
r 2 R ′ ′ + 2 r R ′ − l ( l + 1 ) R = 0 r^2R''+2rR'-l(l+1)R=0 r2R′′+2rR′−l(l+1)R=0
其两个线性独立的解为 r l , 1 / r l + 1 r^l,1/r^{l+1} rl,1/rl+1 较为简单，下面着重讨论 k ≠ 0 k\neq0 k​=0 的情形

线性独立解

l + 1 / 2 l+1/2 l+1/2 阶贝塞尔方程有如下几种解
J l + 1 / 2 ( x ) ,   J − ( l + 1 / 2 ) ( x ) ,   N l + 1 / 2 ( x ) ,   H l + 1 / 2 ( 1 ) ( x ) ,   H l + 1 / 2 ( 2 ) ( x ) J_{l+1/2}(x),\ J_{-(l+1/2)}(x),\ N_{l+1/2}(x),\ H^{(1)}_{l+1/2}(x),\ H^{(2)}_{l+1/2}(x) Jl+1/2​(x), J−(l+1/2)​(x), Nl+1/2​(x), Hl+1/2(1)​(x), Hl+1/2(2)​(x)
其中任取两个就组成方程 (3.2) 的线性独立解。这样求贝塞尔方程 (3.1) 的线性独立解就是下列五种任取两种
球贝塞尔函数
j l ( x ) = π 2 x J l + 1 / 2 ( x ) , j − l ( x ) = π 2 x J − l + 1 / 2 ( x ) j_l(x)=\sqrt{\frac{\pi}{2x}}J_{l+1/2}(x),\\ j_{-l}(x)=\sqrt{\frac{\pi}{2x}}J_{-l+1/2}(x) jl​(x)=2xπ​ ​Jl+1/2​(x),j−l​(x)=2xπ​ ​J−l+1/2​(x)
球诺依曼函数
n l = π 2 x N l + 1 / 2 ( x ) n_l=\sqrt{\frac{\pi}{2x}}N_{l+1/2}(x) nl​=2xπ​ ​Nl+1/2​(x)
球汉克儿函数
h l ( 1 ) ( x ) = π 2 x H l + 1 / 2 ( 1 ) ( x ) , h l ( 2 ) ( x ) = π 2 x H l + 1 / 2 ( 2 ) ( x ) h^{(1)}_l(x)=\sqrt{\frac{\pi}{2x}}H^{(1)}_{l+1/2}(x),\\ h^{(2)}_l(x)=\sqrt{\frac{\pi}{2x}}H^{(2)}_{l+1/2}(x) hl(1)​(x)=2xπ​ ​Hl+1/2(1)​(x),hl(2)​(x)=2xπ​ ​Hl+1/2(2)​(x)
球汉克儿函数由定义知 h l ( 1 ) ( x ) = j l ( x ) + i n l ( x ) , h l ( 2 ) ( x ) = j l ( x ) − i n l ( x ) h^{(1)}_l(x)=j_l(x)+\mathrm in_l(x),\quad h^{(2)}_l(x)=j_l(x)-\mathrm in_l(x) hl(1)​(x)=jl​(x)+inl​(x),hl(2)​(x)=jl​(x)−inl​(x)

初等函数表示式
j 0 ( x ) = sin ⁡ x x , j − 1 ( x ) = cos ⁡ x x j_0(x)=\cfrac{\sin x}{x},\quad j_{-1}(x)=\cfrac{\cos x}{x} j0​(x)=xsinx​,j−1​(x)=xcosx​

n l ( x ) = ( − 1 ) l + 1 j − ( l + 1 ) ( x ) n 0 ( x ) = cos ⁡ x x , n − 1 ( x ) = sin ⁡ x x n_l(x)=(-1)^{l+1}j_{-(l+1)}(x) \\n_0(x)=\cfrac{\cos x}{x},\quad n_{-1}(x)=\cfrac{\sin x}{x} nl​(x)=(−1)l+1j−(l+1)​(x)n0​(x)=xcosx​,n−1​(x)=xsinx​

---

1. 对于齐次线性微分方程标准形式
   y ′ ′ + p ( x ) y ′ + q ( x ) y = 0 y''+p(x)y'+q(x)y=0 y′′+p(x)y′+q(x)y=0 ↩︎

2. Γ \Gamma Γ 函数性质： Γ ( s + 1 ) = s Γ ( s + 1 ) \Gamma(s+1)=s\Gamma(s+1) Γ(s+1)=sΓ(s+1)
   Γ ( ν + 1 ) = ν ! ν \Gamma(ν+1)=ν!\quad ν Γ(ν+1)=ν!ν为正整数。 ↩︎ ↩︎