1 概率公式
条件概率: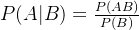
全概率公式:
贝叶斯公式(Bayes):
2 贝叶斯公式
2.1 贝叶斯公式带来的思考
给定某些样本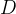 ,在这些样本中计算某结论
,在这些样本中计算某结论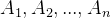 出现的概率,即
出现的概率,即
 贝叶斯公式
贝叶斯公式
 样本给定,则对于任何
样本给定,则对于任何 是常数,仅为归一化因子。
是常数,仅为归一化因子。
 :忽略
:忽略
 :若这些结论
:若这些结论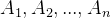 的先验概率相等(或近似),则可以由此推导。
的先验概率相等(或近似),则可以由此推导。
2.2 贝叶斯公式的应用
金条问题:

设这三个箱子为B=1,B=2,B=3, 两块贵金属为M=G(金条),M=S(银条)
所以已知:



问题就转化为求
解答:
2.3 贝叶斯网络
- 把某个研究系统中涉及到的随机变量,根据是否条件独立绘制在一个有向图中,就形成了贝叶斯网络。
- 贝叶斯网络(Bayesian Network),又称有向无环图模型,是一种概率图模型之一,根据概率图的拓扑结构,考察一组随机变量
 及其
及其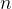 组条件概率分布。
组条件概率分布。
- 概率图模型分为马尔可夫网络模型(无向图)和贝叶斯网络模型(有向图)。
- 一般而言,贝叶斯网络的有向无环图中的节点表示随机变量,它们可以是可观察到的变量,或隐变量、未知参数等。连接两个节点的箭头代表此两个随机变量是具有因果关系(或非条件独立)。若两个节点间以一个单箭头连接在一起,表示其中一个节点是“因(parents)”,另一个是‘果(children)”,两节点就会产生一个条件概率值。
- 一个简单的贝叶斯网络
2.4 全贝叶斯网络
每一对结点之间都有边连接


举例说明:当K=5时
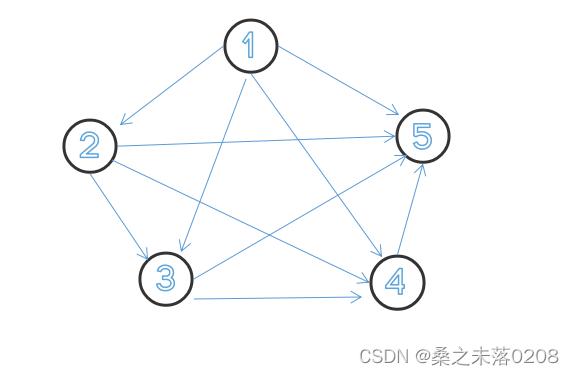
2.5 "正常"的贝叶斯网络
- 有些边缺失
- 如下图所示:直观上
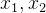 独立,
独立, 在
在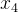 给定条件下独立
给定条件下独立
-
 的联合分布为:
的联合分布为:

举例说明:
例一:
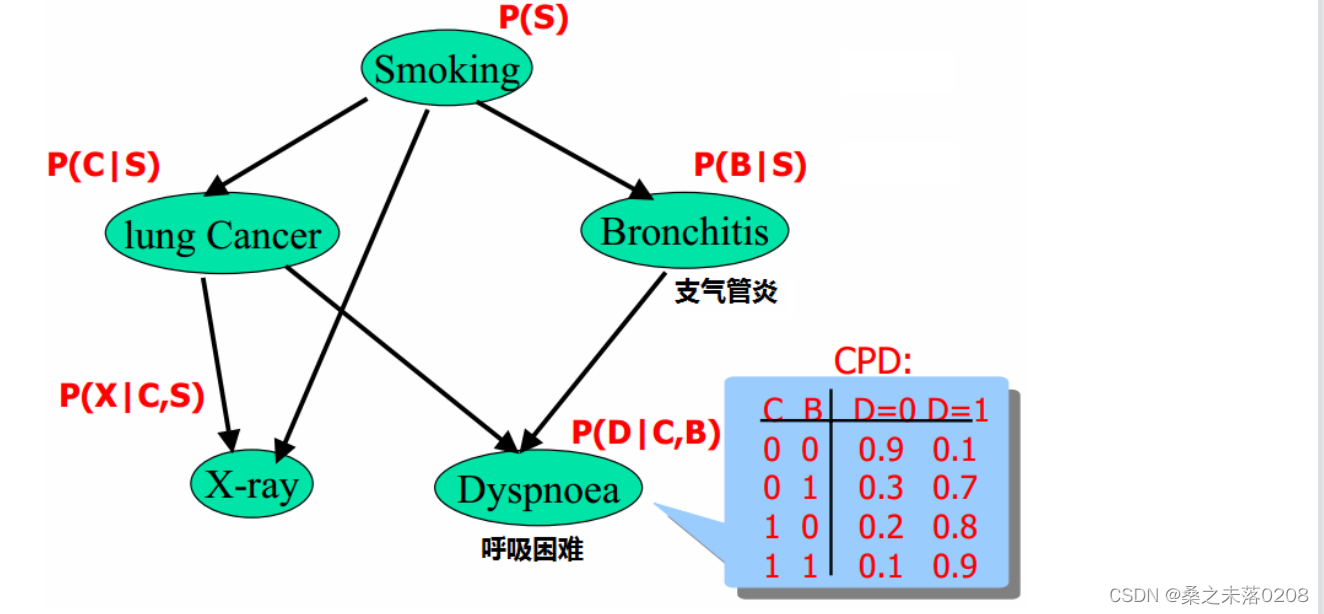
由于呼吸困难(D)所造成的原因有肺癌(C)和支气管炎(B),所以才有上表(CPD)。
例二:
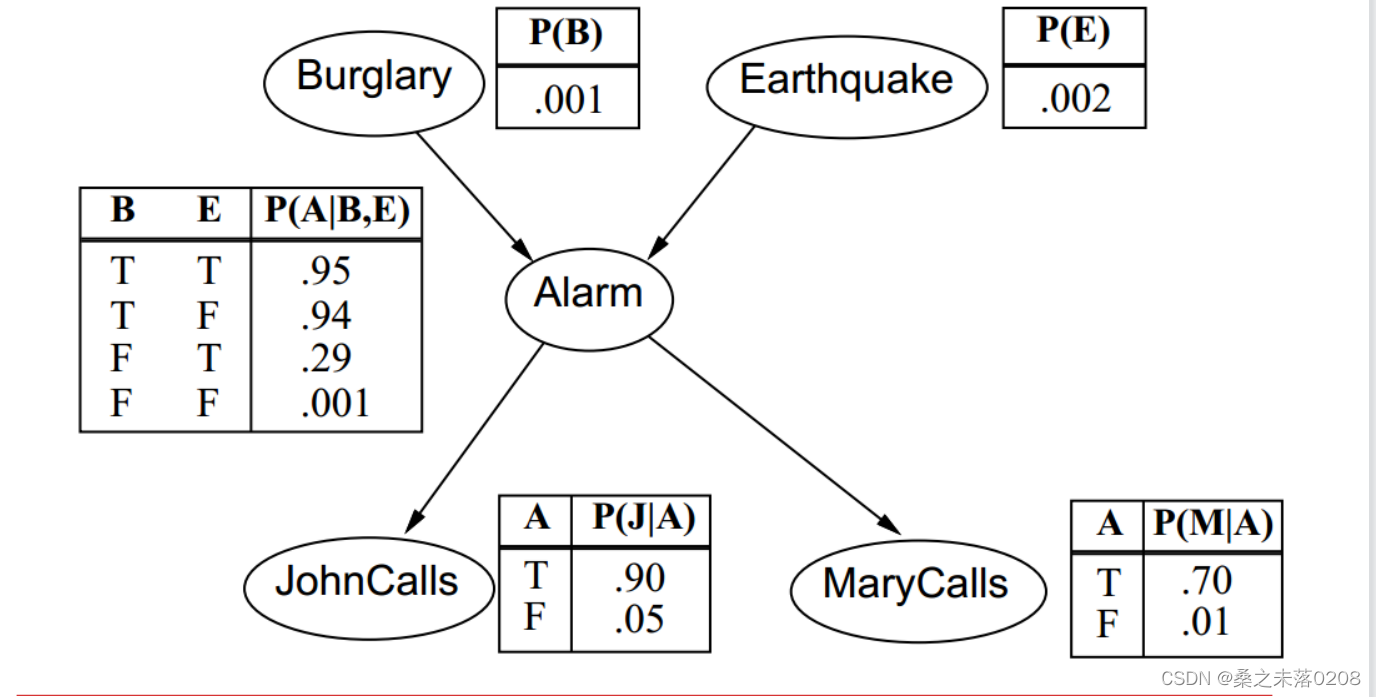
全部随机变量的联合分布为:

实际上,如果需要求联合分布,仅需给出拓扑图,以及各个随机变量之间的概率分布表即可。
2.6 “特殊”的贝叶斯网络

通过贝叶斯网络判定条件独立:
(1)情况一:tail-to-tail
由图可看出:
所以:
又因为:
所以:
即在c给定条件下,a和b被阻断,是独立的。
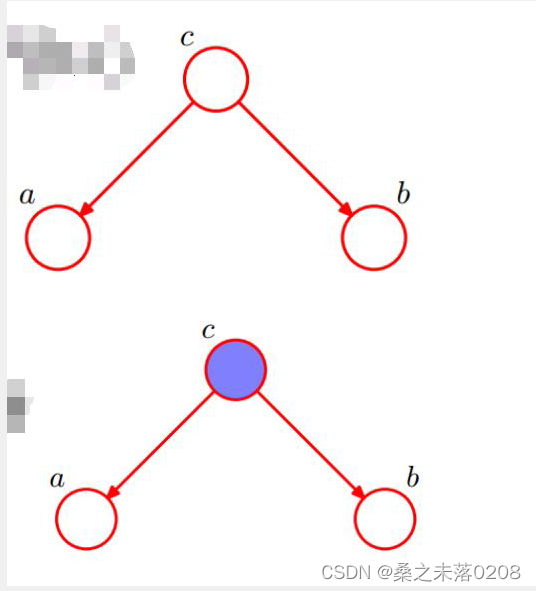
(2)情况二:head-to-tail
由于
所以有:
![P(a,b|c)=P(a,b,c)/P(c)=[P(a)\cdot P(c|a)\cdot P(b|c)] /P(c)=[P(a,c)\cdot P(b|c)]/P(c)=P(a|c)\cdot P(b|c)](https://latex.csdn.net/eq?P%28a%2Cb%7Cc%29%3DP%28a%2Cb%2Cc%29/P%28c%29%3D%5BP%28a%29%5Ccdot%20P%28c%7Ca%29%5Ccdot%20P%28b%7Cc%29%5D%20/P%28c%29%3D%5BP%28a%2Cc%29%5Ccdot%20P%28b%7Cc%29%5D/P%28c%29%3DP%28a%7Cc%29%5Ccdot%20P%28b%7Cc%29)
即在c给定条件下,a和b被阻断,是独立的。

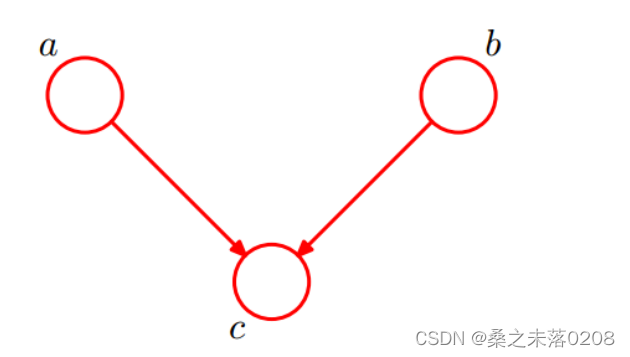
(3)情况三:head-to-head
由于
所以有:
从而:
即在c未知的条件下,a和b被阻断,是独立的。
2.7 将上述结点推广至结点集

ps:有D-separation可知,在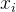 给定的条件下,
给定的条件下, 的分布和
的分布和 条件独立。即:
条件独立。即: 的分布状态只和
的分布状态只和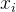 有关,和其他变量条件独立,这种顺次演变的随机过程模型,叫做马尔科夫模型。
有关,和其他变量条件独立,这种顺次演变的随机过程模型,叫做马尔科夫模型。

- 隐马尔科夫模型(HMM,Hidden Markov Model)可用标注问题,在语音识别、NLP、生物信息、模式识别等领域被实践证明是有效的算法。
- HMM是关于时序的概率模型,描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。
- 隐马尔科夫模型随机生成的状态的序列,称为状态序列;每个状态生成一个观测,由此产生的观测随机序列,称为观测序列。序列的每个位置可看做是一个时刻。空间序列也可使用该模型,如分析DNA。
2.8 贝叶斯网络的用途

