引言
说到底,回归任务都是寻找特征 与目标
与目标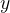 之间的关系,我们认为每一个特征或多或少,或积极或消极地对目标产生着影响,我们期望寻找数学表达式来表达出这种影响。
之间的关系,我们认为每一个特征或多或少,或积极或消极地对目标产生着影响,我们期望寻找数学表达式来表达出这种影响。
一、回归模型
想象一下描述特征 与目标
与目标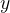 之间最简单明了的关系是什么?
之间最简单明了的关系是什么?
当然是线性关系了;每个特征占一个权重比例,影响着目标的表达。
1.1模型表达式
于是,我们构造 的模型表达式
的模型表达式
其中 是输入的t维度特征向量,被称为自变量(independent variables);
是输入的t维度特征向量,被称为自变量(independent variables);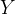 是我们所寻求的目标(target)。
是我们所寻求的目标(target)。
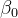 被称为截距(intercept);
被称为截距(intercept); 被称为斜率参数(slope coefficients);
被称为斜率参数(slope coefficients); 是误差项(error term),与模型无关,服从于正态分布
是误差项(error term),与模型无关,服从于正态分布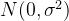 。
。
很形象的是,线性模型服从LINE准则,即
Linearity)线性 – 目标和自变量之间的关系是线性的
Independence)独立性 – 误差项相互独立
Normality)正态性 – 误差项服从正态分布
Equal variance)方差相等 – 误差项同方差
1.2一元线性回归
一元线性回归(Simple Linear Regression)顾名思义,自变量只有一个特征,是一维的,其表达式
对于二维坐标系而言,一元线性回归可视化就容易明朗的多。

点是实际值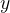 ,对应直线为模型的预测值
,对应直线为模型的预测值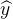 ,可以看到两者之间总是有一些距离的,是随机误差作用的结果。
,可以看到两者之间总是有一些距离的,是随机误差作用的结果。
二、参数估计
好了,模型已经有了,我们该如何确定斜率参数与截距项呢?
以一元线性回归为例,我们当然希望我们的预测与实际越接近越好,于是我们用损失 来衡量预测偏离实际的程度;
来衡量预测偏离实际的程度;
然而这种偏差时正时负,会相互抵消,于是我们用损失的平方之和来评判模型是否能很好的预测给定的数据:

我们称上式为残差平方和(residual sum of squares ,RSS),我们希望通过改变 使得这个损失最小,于是
使得这个损失最小,于是 就是模型待估计的参数(coefficients)。
就是模型待估计的参数(coefficients)。



其中 是样本均值,
是样本均值, 是目标均值,
是目标均值, 是我们估计的参数
是我们估计的参数
值得注意的一点是,一元线性回归是存在最优解的;
我们计算其损失的Hessian 矩阵

讨论矩阵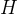 的特征值,相当于讨论矩阵
的特征值,相当于讨论矩阵 的特征值
的特征值


讨论 项,经数学推导发现他恒非负
项,经数学推导发现他恒非负
所以 的两个根其中一个大于0,另一个大于等于0(当
的两个根其中一个大于0,另一个大于等于0(当
 时该特征根为0)。
时该特征根为0)。
由此得知矩阵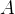 正定或者半正定,于是又矩阵
正定或者半正定,于是又矩阵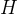 正定半正定可见损失函数是凸函数(凸优化看这一篇
正定半正定可见损失函数是凸函数(凸优化看这一篇
凸优化(Quasi convex optimization)与梯度下降(Grad descent) https://blog.csdn.net/a2333333_/article/details/130614781?spm=1001.2014.3001.5501),必定存在极值点。
https://blog.csdn.net/a2333333_/article/details/130614781?spm=1001.2014.3001.5501),必定存在极值点。
三、多元线性回归
3.1多元线性回归表达式
上述的表达式 便是多元线性回归(Multiple Linear Regression),它和一元的不同在于,特征多了起来。
便是多元线性回归(Multiple Linear Regression),它和一元的不同在于,特征多了起来。
对于这一串表达式,我们用简介的矩阵乘法来表示

于是有 ,
,
3.2参数估计
其中 是待估计参数;
是待估计参数;
扩展上文所提到的,一元线性回归是凸优化问题,多元线性回归同样是凸优化问题,其损失函数是严格的凸函数,一定在区间内存在最优值,于是有

这便要求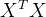 是可逆的,这便涉及到高等代数线性空间的理论了。
是可逆的,这便涉及到高等代数线性空间的理论了。
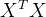 可逆,即仅存在0向量
可逆,即仅存在0向量 使得
使得 ,而
,而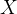 与
与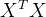 有着相同的零空间,于是要求
有着相同的零空间,于是要求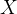 列满秩,即样本之间线性无关。
列满秩,即样本之间线性无关。
当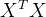 不可逆,也就是
不可逆,也就是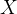 不满足列满秩了,此时输入的多个样本之间线性相关了,即至少存在一个样本可以被其他样本的线性组合所表示,这时候称自变量存在完全多重共线性(perfect multicollinearity)。此时需要去掉那些由其他变量线性组合而成的变量,或者收集更多的特征使样本间不存在线性关系
不满足列满秩了,此时输入的多个样本之间线性相关了,即至少存在一个样本可以被其他样本的线性组合所表示,这时候称自变量存在完全多重共线性(perfect multicollinearity)。此时需要去掉那些由其他变量线性组合而成的变量,或者收集更多的特征使样本间不存在线性关系
当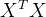 可逆,但是有样本几乎可以被其他样本所线性表示了,此时称当变量间存在准多重共线性(near multicollinearity)。此时可以通过降维来解决问题。
可逆,但是有样本几乎可以被其他样本所线性表示了,此时称当变量间存在准多重共线性(near multicollinearity)。此时可以通过降维来解决问题。