一下理解均为本人的个人理解,如有错误,欢迎指出
logistic回归又称logistic回归分析,是一种广义的线性回归分析模型
设想有这么一种情况,有一组数据,因变量只有0和1两种取值,我们想用一个函数去拟合这组数据,传统的线性回归的因变量取值是连续的,而逻辑回归用于处理因变量取值0-1时的函数拟合的情况,逻辑回归处理的是令人头疼的离散值连续化的问题(参考资料逻辑回归)
对于一个事物,在已知自变量的情况下,如果这个事物的取值为1,逻辑回归不是单纯的认为其取值为1,而是认为相对于取值为0,该事物取值为1的概率更大,若使用y表示已知自变量的情况下,该事物取值为1的概率,则1-y表示已知自变量的情况下,该事物取值为0的概率,则使用:
y 1 − y ( 式 1.0 ) \frac{y}{1-y}(式1.0) 1−yy(式1.0)
表示已知自变量的情况下,该事物作为取值为1的相对可能性,式1.0又称为几率,通过概率角度,我们将因变量的0-1取值转变为 ( 0 , + ∞ ) (0,+\infin) (0,+∞)区间的连续值,但是,线性回归的取值区间是 ( − ∞ , + ∞ ) (-\infin,+\infin) (−∞,+∞),所以我们还需要一个手段,将几率的取值范围扩展为 ( − ∞ , + ∞ ) (-\infin,+\infin) (−∞,+∞),逻辑回归采用了对数函数,即:
ln ( y 1 − y ) ( 式 1.1 ) \ln(\frac{y}{1-y})(式1.1) ln(1−yy)(式1.1)
式1.1称为对数几率,式1.1的取值为 ( − ∞ , + ∞ ) (-\infin,+\infin) (−∞,+∞),此时有:
ln ( y 1 − y ) = w T x + b ( 式 1.2 ) \ln(\frac{y}{1-y})=w^Tx+b(式1.2) ln(1−yy)=wTx+b(式1.2)
对上式进行化简得:
y = 1 1 + e − ( w T x + b ) ( 式 1.3 ) y=\frac{1}{1+e^{-(w^Tx+b)}}(式1.3) y=1+e−(wTx+b)1(式1.3)
该函数即为sigmoid函数复合
w
T
x
+
b
w^Tx+b
wTx+b 后获得,sigmoid函数长这样:
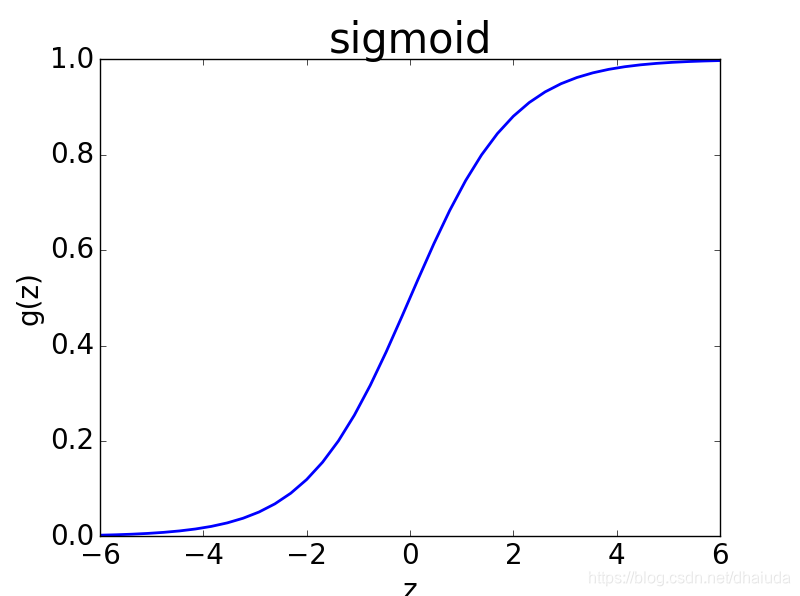
这个函数因变量取值为(0,1),当自变量大到一定程度时,sigmoid函数的取值将趋近于1。
对于因变量取值为1的数据,逻辑回归只是认为该数据取值为1的相对概率较大,即对数几率比较大,那么,只需让式1.1的输出尽可能大,即y尽可能大,对于取值为0的数据,只需让式1.1的输出尽可能小,即y尽可能小。
说白了,逻辑回归只保证在已知自变量的情况下,对于取值为1的数据,式1.3的取值将会尽可能的趋近于1,对于取值为0的数据,式1.3的取值将会尽可能的趋近于0,但是并没有给出区分取值0-1的区分点,这就需要我们根据自己的实际需要进行确定,但这也给了逻辑回归一定的灵活性
经过上述分析,我们已经获得了逻辑回归的表达式——式1.3,接下来,该怎么求解
w
、
b
w、b
w、b?依据线性回归的思想,我们很容易想到通过均方误差作为损失函数,如下:
上图中的
ϕ
\phi
ϕ函数即为sigmoid函数,但是这个函数是非凸函数,给定一组样本,考虑二维的情况,其函数图像如下:
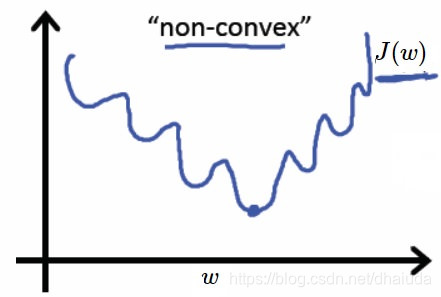
如果使用常用的梯度下降法、牛顿法,将很容易陷入局部最小,也就是说,我们应该换一个损失函数,该损失函数为凸函数
若使用后验概率
p
(
y
=
1
∣
x
)
p(y=1|x)
p(y=1∣x)来表示y,即已知x的情况下,y取值为1的概率,则则
p
(
y
=
0
∣
x
)
p(y=0|x)
p(y=0∣x)表示已知x的情况下,y取值为0的概率,式1.2可重写为:
ln ( p ( y = 1 ∣ x ) p ( y = 0 ∣ x ) ) = w T x + b ( 式 2.0 ) \ln(\frac{p(y=1|x)}{p(y=0|x)})=w^Tx+b(式2.0) ln(p(y=0∣x)p(y=1∣x))=wTx+b(式2.0)
又有:
p ( y = 1 ∣ x ) + p ( y = 0 ∣ x ) = 1 ( 式 2.1 ) p(y=1|x)+p(y=0|x)=1(式2.1) p(y=1∣x)+p(y=0∣x)=1(式2.1)
连立式2.0与2.1可得(初等解方程的问题,就不再列出过程):
p
(
y
=
1
∣
x
)
=
e
w
T
x
+
b
1
+
e
w
T
x
+
b
(
式
2.2
)
p
(
y
=
0
∣
x
)
=
1
1
+
e
w
T
x
+
b
(
式
2.3
)
p(y=1|x)=\frac{e^{w^Tx+b}}{1+e^{w^Tx+b}}(式2.2) \\ p(y=0|x)=\frac{1}{1+e^{w^Tx+b}} (式2.3)
p(y=1∣x)=1+ewTx+bewTx+b(式2.2)p(y=0∣x)=1+ewTx+b1(式2.3)
从逻辑回归的角度出发,假设有m个样本,样本与样本间相互独立(即一个样本的出现不会影响其他样本的出现),我们来梳理一下我们现有的条件
满足使用极大似然估计的条件,则最大化对数似然:
ι ( w , b ) = ∑ i = 1 m ln ( y i ∣ x i ; w , b ) ( 式 2.4 ) \iota(w,b)=\sum_{i=1}^m\ln(y_i|x_i;w,b)(式2.4) ι(w,b)=i=1∑mln(yi∣xi;w,b)(式2.4)
等等,极大似然估计真的很好的解释逻辑回归的思想么?即对于取值为1的样本,式1.3的输出尽可能靠近1 。取值为0的样本,式1.3的输出尽可能靠近0。
首先注意到式(2.2)分子分母同除以
e
(
w
T
x
+
b
)
e^{(w^Tx+b)}
e(wTx+b)就可以得到式1.3 。
极大似然法是想令每个样本属于其真实标记的概率越大越好,那么对于取值为1的样本,极大似然法将使式2.2的取值尽可能大,即y的取值尽可能大,即式1.3的取值尽可能趋近于1,对于取值为0的样本,极大似然法将使式2.3的取值尽可能大,即y的取值尽可能小,即式1.3的取值尽可能趋近于0
对式2.2,2.3使用0-1规划,可得:
ln ( y i ∣ x i ; w , b ) = y i p ( y i = 1 ∣ x i ) + ( 1 − y i ) p ( y i = 0 ∣ x i ) ( 式 2.5 ) \ln(y_i|x_i;w,b)=y_ip(y_i=1|x_i)+(1-y_i)p(y_i=0|x_i)(式2.5) ln(yi∣xi;w,b)=yip(yi=1∣xi)+(1−yi)p(yi=0∣xi)(式2.5)
连立式2.2、2.3、2.4、2.5,可将对数似然转变为(基本的初等变换,这里不列出推导过程):
ι ( w , b ) = ∑ i = 1 m ( ln ( y i e w T x i + b + 1 − y i ) − ln ( 1 + e w T x i + b ) ) ( 式 2.6 ) \iota(w,b)=\sum_{i=1}^m(\ln(y_ie^{w^Tx_i+b}+1-y_i)-\ln(1+e^{w^Tx_i+ b})) (式2.6) ι(w,b)=i=1∑m(ln(yiewTxi+b+1−yi)−ln(1+ewTxi+b))(式2.6)
观察式子 ln ( y i e w T x i + b + 1 − y i ) \ln(y_ie^{w^Tx_i+b}+1-y_i) ln(yiewTxi+b+1−yi),当 y i y_i yi取值为1时,其取值为 w T x i + b w^Tx_i+b wTxi+b,当 y i y_i yi取值为0时,其取值为0,则可用 y i ( w T x i + b ) y_i(w^Tx_i+b) yi(wTxi+b)来表示 ln ( y i e w T x i + b + 1 − y i ) \ln(y_ie^{w^Tx_i+b}+1-y_i) ln(yiewTxi+b+1−yi)
则式2.6可表示为:
ι
(
w
,
b
)
=
∑
i
=
1
m
(
y
i
(
w
T
x
i
+
b
)
−
ln
(
1
+
e
w
T
x
i
+
b
)
)
(
式
2.7
)
\iota(w,b)=\sum_{i=1}^m(y_i(w^Tx_i+b)-\ln(1+e^{w^Tx_i+ b})) (式2.7)
ι(w,b)=i=1∑m(yi(wTxi+b)−ln(1+ewTxi+b))(式2.7)
最大化式2.7等价于最小化式2.8
ι ( w , b ) = ∑ i = 1 m ( − y i ( w T x i + b ) + ln ( 1 + e w T x i + b ) ) ( 式 2.8 ) \iota(w,b)=\sum_{i=1}^m(-y_i(w^Tx_i+b)+\ln(1+e^{w^Tx_i+ b})) (式2.8) ι(w,b)=i=1∑m(−yi(wTxi+b)+ln(1+ewTxi+b))(式2.8)
式2.8的海森矩阵为半正定,故其为凸函数,可以使用最优化理论获得其最小值
这里我们使用梯度下降法,下面给出梯度下降法的推导过程
令
x
i
x_i
xi表示
(
x
i
1
,
x
i
2
,
.
.
.
.
,
x
i
n
)
(x_{i1},x_{i2},....,x_{in})
(xi1,xi2,....,xin),即数据具有n个特征,
w
w
w表示
(
w
1
,
w
2
,
.
.
.
.
.
,
w
n
)
(w_1,w_2,.....,w_n)
(w1,w2,.....,wn),共有m组数据,
y
i
y_i
yi表示第i组数据的取值,式2.8对
w
、
b
w、b
w、b求导得
∂
ι
∂
w
1
=
∑
i
=
1
m
(
−
y
i
x
i
1
)
+
∑
i
=
1
m
(
ln
(
1
+
e
w
T
x
i
+
b
)
x
i
1
)
∂
ι
∂
w
2
=
∑
i
=
1
m
(
−
y
i
x
i
2
)
+
∑
i
=
1
m
(
ln
(
1
+
e
w
T
x
i
+
b
)
x
i
2
)
.
.
.
.
.
∂
ι
∂
w
n
=
∑
i
=
1
m
(
−
y
i
x
i
n
)
+
∑
i
=
1
m
(
ln
(
1
+
e
w
T
x
i
+
b
)
x
i
n
)
∂
ι
∂
b
=
∑
i
=
1
m
(
−
y
i
)
+
∑
i
=
1
m
(
ln
(
1
+
e
w
T
x
i
+
b
)
)
\begin{aligned} & \frac{\partial \iota}{\partial w_1}=\sum_{i=1}^m(-y_{i}x_{i1})+\sum_{i=1}^m(\ln(1+e^{w^Tx_i+b})x_{i1})\\ & \frac{\partial \iota}{\partial w_2}=\sum_{i=1}^m(-y_{i}x_{i2})+\sum_{i=1}^m(\ln(1+e^{w^Tx_i+b})x_{i2})\\ &.....\\ &\frac{\partial \iota}{\partial w_n}=\sum_{i=1}^m(-y_{i}x_{in})+\sum_{i=1}^m(\ln(1+e^{w^Tx_i+b})x_{in})\\ &\frac{\partial \iota}{\partial b}=\sum_{i=1}^m(-y_{i})+\sum_{i=1}^m(\ln(1+e^{w^Tx_i+b})) \end{aligned}
∂w1∂ι=i=1∑m(−yixi1)+i=1∑m(ln(1+ewTxi+b)xi1)∂w2∂ι=i=1∑m(−yixi2)+i=1∑m(ln(1+ewTxi+b)xi2).....∂wn∂ι=i=1∑m(−yixin)+i=1∑m(ln(1+ewTxi+b)xin)∂b∂ι=i=1∑m(−yi)+i=1∑m(ln(1+ewTxi+b))
将上面这一坨式子写成矩阵的形式,则有:
{
∂
ι
∂
w
1
∂
ι
∂
w
2
.
.
∂
ι
∂
w
n
∂
ι
∂
b
}
=
{
x
11
x
21
.
.
.
x
m
1
x
12
x
22
.
.
.
x
m
2
.
.
.
.
.
.
.
.
x
1
n
x
2
n
.
.
.
x
m
n
1
1
1
1
}
{
−
y
1
−
y
2
.
.
−
y
m
}
+
{
x
11
x
21
.
.
.
x
m
1
x
12
x
22
.
.
.
x
m
2
.
.
.
.
.
.
.
.
x
1
n
x
2
n
.
.
.
x
m
n
1
1
1
1
}
{
ln
(
1
+
e
w
T
x
1
+
b
)
e
w
T
x
1
+
b
ln
(
1
+
e
w
T
x
2
+
b
)
e
w
T
x
2
+
b
.
.
ln
(
1
+
e
w
T
x
m
+
b
)
e
w
T
x
m
+
b
}
\left\{ \begin{matrix} \frac{\partial \iota}{\partial w_1}\\ \frac{\partial \iota}{\partial w_2}\\ .\\ .\\ \frac{\partial \iota}{\partial w_n}\\ \frac{\partial \iota}{\partial b} \end{matrix} \right\} = \left\{ \begin{matrix} x_{11} & x_{21} & ... & x_{m1} \\ x_{12} & x_{22} & ... & x_{m2} \\ . & . & . &.\\ . & . & . &.\\ x_{1n} & x_{2n} & ... & x_{mn} \\ 1 & 1 & 1 &1\\ \end{matrix} \right\} \left\{ \begin{matrix} -y_1\\ -y_2\\ .\\ .\\ -y_m \end{matrix} \right\}+ \left\{ \begin{matrix} x_{11} & x_{21} & ... & x_{m1} \\ x_{12} & x_{22} & ... & x_{m2} \\ . & . & . &.\\ . & . & . &.\\ x_{1n} & x_{2n} & ... & x_{mn} \\ 1 & 1 & 1 &1\\ \end{matrix} \right\} \left\{ \begin{matrix} \ln(1+e^{w^Tx_1+b})e^{w^Tx_1+b} \\ \ln(1+e^{w^Tx_2+b})e^{w^Tx_2+b} \\ . \\ . \\ \ln(1+e^{w^Tx_m+b})e^{w^Tx_m+b} \\ \end{matrix} \right\}
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∂w1∂ι∂w2∂ι..∂wn∂ι∂b∂ι⎭⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎫=⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧x11x12..x1n1x21x22..x2n1...........1xm1xm2..xmn1⎭⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎫⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧−y1−y2..−ym⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫+⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧x11x12..x1n1x21x22..x2n1...........1xm1xm2..xmn1⎭⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎫⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧ln(1+ewTx1+b)ewTx1+bln(1+ewTx2+b)ewTx2+b..ln(1+ewTxm+b)ewTxm+b⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫
令
X
T
=
{
x
11
x
21
.
.
.
x
m
1
x
12
x
22
.
.
.
x
m
2
.
.
.
.
.
.
.
.
x
1
n
x
2
n
.
.
.
x
m
n
1
1
1
1
}
X^T=\left\{ \begin{matrix} x_{11} & x_{21} & ... & x_{m1} \\ x_{12} & x_{22} & ... & x_{m2} \\ . & . & . &.\\ . & . & . &.\\ x_{1n} & x_{2n} & ... & x_{mn} \\ 1 & 1 & 1 &1\\ \end{matrix} \right\}
XT=⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧x11x12..x1n1x21x22..x2n1...........1xm1xm2..xmn1⎭⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎫
Y
=
{
y
1
y
2
.
.
y
m
}
Y=\left\{ \begin{matrix} y_1\\ y_2\\ .\\ .\\ y_m \end{matrix} \right\}
Y=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧y1y2..ym⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫
H
=
{
ln
(
1
+
e
w
T
x
1
+
b
)
e
w
T
x
1
+
b
ln
(
1
+
e
w
T
x
2
+
b
)
e
w
T
x
2
+
b
.
.
ln
(
1
+
e
w
T
x
m
+
b
)
e
w
T
x
m
+
b
}
H= \left\{ \begin{matrix} \ln(1+e^{w^Tx_1+b})e^{w^Tx_1+b} \\ \ln(1+e^{w^Tx_2+b})e^{w^Tx_2+b} \\ . \\ . \\ \ln(1+e^{w^Tx_m+b})e^{w^Tx_m+b} \\ \end{matrix} \right\}
H=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧ln(1+ewTx1+b)ewTx1+bln(1+ewTx2+b)ewTx2+b..ln(1+ewTxm+b)ewTxm+b⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫
则
w
w
w的更新值
w
,
w^,
w,可表示为:
w , = w − α ( X T ( − Y ) + X T H ) w^,=w-\alpha( X^T(-Y)+X^TH) w,=w−α(XT(−Y)+XTH)
分类:因变量取值0-1本身可看成二分类问题,本文介绍的逻辑回归模型适用于二分类问题
对于分类问题,可以使用ROC和AUC进行度量,这里偷个懒,不自己写了(两个星期打了三场比赛一场答辩,都要吐了,呕)可以参考:机器学习之分类器性能指标之ROC曲线、AUC值,内容讲解的是正确的,和周志华老师的《机器学习》中讲的差不多,只是更详细
总结自百度百科 数模缺大腿
因变量满足二项分布
从推导过程可以看到,因变量取值只有两种,并且要求相互独立,因为相互独立是使用极大似然法的前提,百度百科上也说过残差满足二项分布,其实只要因变量满足二项分布,残差也一定满足,因为残差的取值也只有两种
逻辑回归是一个线性模型,因为逻辑回归的分界面是一个直线(平面)
import torch
from torch import nn
import matplotlib.pyplot as plt
import numpy as np
# 假数据
n_data = torch.ones(100, 2) # 数据的基本形态
x0 = torch.normal(2 * n_data, 1) # 类型0 x data (tensor), shape=(100, 2)
y0 = torch.zeros(100) # 类型0 y data (tensor), shape=(100, 1)
x1 = torch.normal(-2 * n_data, 1) # 类型1 x data (tensor), shape=(100, 1)
y1 = torch.ones(100) # 类型1 y data (tensor), shape=(100, 1)
# 注意 x, y 数据的数据形式是一定要像下面一样 (torch.cat 是在合并数据)
x_data = torch.cat((x0, x1), 0).type(torch.FloatTensor) # FloatTensor = 32-bit floating
y_data = torch.cat((y0, y1), 0).type(torch.FloatTensor) # LongTensor = 64-bit integer
class LogisticRegression(nn.Module):
def __init__(self):
super(LogisticRegression, self).__init__()
self.lr = nn.Linear(2, 1)
self.sm = nn.Sigmoid()
def forward(self, x):
x = self.lr(x)
x = self.sm(x)
return x
logistic_model = LogisticRegression()
if torch.cuda.is_available():
logistic_model.cuda()
# 定义损失函数和优化器
criterion = nn.BCELoss()
optimizer = torch.optim.SGD(logistic_model.parameters(), lr=1e-3, momentum=0.9)
# 开始训练
for epoch in range(10000):
out = logistic_model(x_data)
loss = criterion(out, y_data)
print_loss = loss.data.item()
mask = out.ge(0.5).float() # 以0.5为阈值进行分类
correct = (mask == y_data).sum() # 计算正确预测的样本个数
acc = correct.item() / x_data.size(0) # 计算精度
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 每隔20轮打印一下当前的误差和精度
if (epoch + 1) % 20 == 0:
print('*' * 10)
print('epoch {}'.format(epoch + 1)) # 训练轮数
print('loss is {:.4f}'.format(print_loss)) # 误差
print('acc is {:.4f}'.format(acc)) # 精度
# 结果可视化
w0, w1 = logistic_model.lr.weight[0]
w0 = float(w0.item())
w1 = float(w1.item())
b = float(logistic_model.lr.bias.item())
plot_x = np.arange(-7, 7, 0.1)
plot_y = (-w0 * plot_x - b) / w1
plt.scatter(x_data.data.numpy()[:, 0], x_data.data.numpy()[:, 1], c=y_data.data.numpy(), s=100, lw=0, cmap='RdYlGn')
plt.plot(plot_x, plot_y)
plt.show()
运行结果:

如果您想了解更多有关深度学习、机器学习基础知识,或是java开发、大数据相关的知识,欢迎关注我们的公众号,我将在公众号上不定期更新深度学习、机器学习相关的基础知识,分享深度学习中有趣文章的阅读笔记。

