目录
0、引言
一、数值积分的积分思想
1、中矩形公式
2、梯形公式
3、辛普森公式
二、求积公式的余项和代数精度
三、插值型求积公式
四、牛顿--柯特斯公式 (N-C公式)
五、复化求积法
1、复化梯形公式
2、复化辛普森公式 (要求 n 为偶数)
六、代码实现
0、引言
在高数中,可以根据  ,求得积分。但是如果
,求得积分。但是如果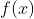 存在以下两种情况:
存在以下两种情况:
-
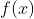 是离散函数
是离散函数
- 无法求得原函数
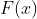
那么对于这种情况,就可以利用数值积分。
所谓数值积分,指利用被积函数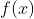 在有限个点上的函数值来计算积分近似值的一种方法。
在有限个点上的函数值来计算积分近似值的一种方法。
一、数值积分的积分思想
积分中值定理: ![\int_{a}^{b}f(x)dx = (b-a)f(\xi ),\xi \in [a,b]](https://private.codecogs.com/gif.latex?%5Cint_%7Ba%7D%5E%7Bb%7Df%28x%29dx%20%3D%20%28b-a%29f%28%5Cxi%20%29%2C%5Cxi%20%5Cin%20%5Ba%2Cb%5D)
一重积分可以理解为求面积,积分中值定理可以看成:在![x\in [a,b]](https://private.codecogs.com/gif.latex?x%5Cin%20%5Ba%2Cb%5D) 上,函数
上,函数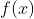 与
与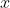 轴的面积等于以
轴的面积等于以 为长,
为长,![\xi \in [a,b]](https://private.codecogs.com/gif.latex?%5Cxi%20%5Cin%20%5Ba%2Cb%5D) 中一点函数值
中一点函数值 为宽的矩形的面积。
为宽的矩形的面积。

1、中矩形公式

2、梯形公式

3、辛普森公式
![\int_{a}^{b}f(x)dx\approx (b-a)\cdot \frac{1}{6}[f(a)+4f(\frac{a+b}{2})+f(b)]](https://private.codecogs.com/gif.latex?%5Cint_%7Ba%7D%5E%7Bb%7Df%28x%29dx%5Capprox%20%28b-a%29%5Ccdot%20%5Cfrac%7B1%7D%7B6%7D%5Bf%28a%29+4f%28%5Cfrac%7Ba+b%7D%7B2%7D%29+f%28b%29%5D)
一般情况下,可用: 
 ,其中
,其中  。
。
上式称为数值积分的基本公式,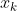 称为求积节点,
称为求积节点,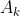 称为求积系数。
称为求积系数。
二、求积公式的余项和代数精度
1、余项

2、代数精度
若数值积分公式对任意的  次的代数多项式都准确成立,而对于
次的代数多项式都准确成立,而对于 却不能成立,则称该数值积分公式的代数精度为
却不能成立,则称该数值积分公式的代数精度为 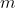 。
。
举个例子理解一下: 求梯形公式的代数精度。
解: 
- 当
 ,
,
- 当
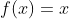 ,
, 
- 当
 ,
, ;
;


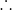 梯形公式的代数精度为1。
梯形公式的代数精度为1。
定理:含有 n+1 个节点的插值型数值积分公式的代数精度至少为 n 。
三、插值型求积公式
已知
则拉格朗日插值可表示为:  ,
, 为 基函数。
为 基函数。




即为 插值型求积公式。其中 
四、牛顿--柯特斯公式 (N-C公式)
牛顿-柯斯特求积公式是插值型求积公式的特殊形式,在插值型求积公式中所取节点是等距时称为牛顿-柯斯特公式。
即,N-C公式为等距节点的插值型求积公式。

在[![[a,b]](https://private.codecogs.com/gif.latex?%5Ba%2Cb%5D) 区间内设置等距的插值节点
区间内设置等距的插值节点 .
.
设节点步长为
则节点 
![\forall x\in [a,b]](https://private.codecogs.com/gif.latex?%5Cforall%20x%5Cin%20%5Ba%2Cb%5D) ,有
,有 

则插值型求积系数:

 变量由
变量由  ,所以变量范围由
,所以变量范围由![[a,b]\rightarrow [0,n]](https://private.codecogs.com/gif.latex?%5Ba%2Cb%5D%5Crightarrow%20%5B0%2Cn%5D) ;
;


 ,与
,与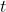 无关的提到积分号之外
无关的提到积分号之外



因为  只与
只与  有关,与
有关,与  ,步长
,步长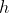 均无关
均无关
而该表达式称之为柯斯特求积系数,记为

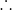 求积系数
求积系数 
N-C公式为:
1、n = 1 (梯形公式)


 就变成了梯形公式
就变成了梯形公式
2、n = 2 (辛普森公式)
 ,
, ,
,

 辛普森公式
辛普森公式
3、n=4
![\int_{a}^{b}f(x)dx = \frac{b-a}{90}[7f(x_{0})+ 32f(x_{1})+12f(x_{2})+32f(x_{3})+7(x_{4})]](https://private.codecogs.com/gif.latex?%5Cint_%7Ba%7D%5E%7Bb%7Df%28x%29dx%20%3D%20%5Cfrac%7Bb-a%7D%7B90%7D%5B7f%28x_%7B0%7D%29+%2032f%28x_%7B1%7D%29+12f%28x_%7B2%7D%29+32f%28x_%7B3%7D%29+7%28x_%7B4%7D%29%5D) ,其中
,其中 
五、复化求积法
当积分区间较大时,C-N求积公式的误差会很大。为减少误差,可以考虑增加节点,但用高次多项式插值导出的公式稳定性不好。所以可以考虑用分段插值函数来代替被积函数。
把![[a,b]](https://private.codecogs.com/gif.latex?%5Ba%2Cb%5D) 分成n 个区间
分成n 个区间![[x_{k-1},x_{k}] (k=1,2,\cdots ,n)](https://private.codecogs.com/gif.latex?%5Bx_%7Bk-1%7D%2Cx_%7Bk%7D%5D%20%28k%3D1%2C2%2C%5Ccdots%20%2Cn%29) ,然后给每个区间上用低阶N-C公式求积(设为
,然后给每个区间上用低阶N-C公式求积(设为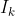 ),则
),则

1、复化梯形公式
![T_{n}= \frac{h}{2}[f(x_{0})+f(x_{1})] + \frac{h}{2}[f(x_{1})+f(x_{2})] + \cdots + \frac{h}{2}[f(x_{n-1})+f(x_{n})]](https://private.codecogs.com/gif.latex?T_%7Bn%7D%3D%20%5Cfrac%7Bh%7D%7B2%7D%5Bf%28x_%7B0%7D%29+f%28x_%7B1%7D%29%5D%20+%20%5Cfrac%7Bh%7D%7B2%7D%5Bf%28x_%7B1%7D%29+f%28x_%7B2%7D%29%5D%20+%20%5Ccdots%20+%20%5Cfrac%7Bh%7D%7B2%7D%5Bf%28x_%7Bn-1%7D%29+f%28x_%7Bn%7D%29%5D)
![= \frac{h}{2}[f(a)+ 2\sum_{k=1}^{n-1}f(x_{k}) + f(b)]](https://private.codecogs.com/gif.latex?%3D%20%5Cfrac%7Bh%7D%7B2%7D%5Bf%28a%29+%202%5Csum_%7Bk%3D1%7D%5E%7Bn-1%7Df%28x_%7Bk%7D%29%20+%20f%28b%29%5D) ,其中
,其中
拓展:变步长梯形公式
定步长复化求积公式的一个明显缺点是:事先很难估计分划数n使结果达到预期精度。由于适当加密分点,精度会有所改善,为此采用自动加密分点的方法,并利用事后估计来控制加密次数,以判断是否达到预期精度,从而停止计算。
- 对所有已存在的子区间进行二分化,区间数由n变为2n
- 利用区间数为n时的积分值Tn以及新增的节点(即原来各子区间的中点)递推出区间数为2n时的积分值T2n
- 利用两次计算结果的差来估计误差,直到满足精度
公式如下:
 ,其中
,其中 
2、复化辛普森公式 (要求 n 为偶数)
![S_{n} = \frac{h}{3}[f(a) + 2\sum_{k=1}^{m-1}f(x_{2k}) + 4\sum_{k=1}^{m}f(x_{2k-1}) +f(b)]](https://private.codecogs.com/gif.latex?S_%7Bn%7D%20%3D%20%5Cfrac%7Bh%7D%7B3%7D%5Bf%28a%29%20+%202%5Csum_%7Bk%3D1%7D%5E%7Bm-1%7Df%28x_%7B2k%7D%29%20+%204%5Csum_%7Bk%3D1%7D%5E%7Bm%7Df%28x_%7B2k-1%7D%29%20+f%28b%29%5D) ,其中
,其中
六、代码实现
1、C++实现
先计算一个简单的,可以求原函数的。如  ,标准答案为
,标准答案为  。程序运行结果为:
。程序运行结果为:

可以看出,复化公式的精度更高一些。
现在,如果要求原函数不可求的,如  ,程序结果为:
,程序结果为:

C++代码:
main文件
#include<iostream>
#include"integral.h"
#include<iomanip>
using namespace std;
const double eps = 1e-8;
int main()
{
double resultT = T(fun2, 1, 2);
cout << "梯形公式计算结果" << "\t" << setprecision(8) << resultT << endl;
double resultS = S(fun2, 1, 2);
cout << "辛普森公式计算结果" << "\t" << setprecision(8) << resultS << endl;
double resultTn = Tn(fun2, 1, 2, 100);
cout << "复化梯形公式计算结果" << "\t" << setprecision(8) << resultTn << endl;
double resultT2n = T2n(fun2, 1, 2, eps);
cout << "变步长梯形公式计算结果" << "\t" << setprecision(8) << resultT2n << endl;
cout << endl;
double resultSn = Sn(fun2, 1, 2);
cout << "复化辛普森公式计算结果" << "\t" << setprecision(8) << resultSn << endl;
}
.h头文件(积分实现部分)
#pragma once
#include<iostream>
using namespace std;
double fun1(double x) {
double y = 1 / x;
return y;
}
double fun2(double x) {
double y = log(3 + pow(x,2)) / (1 + pow(x, 2));
return y;
}
//梯形公式
double T(double(*f)(double), double a, double b) {
double result = 0.0;
result = 0.5 * (b - a) * (f(a) + f(b));
return result;
}
//辛普森公式
double S(double(*f)(double), double a, double b) {
double result = 0.0;
result = 1 / 6.0 * (b - a) * ( f(a) + f(b) + 4 * f( (a + b) / 2.0) );
return result;
}
//复化梯形公式
double Tn(double(*f)(double), double a, double b, int n) {
double result = 0.0;
double h = (b - a) / n;
result = h / 2.0 * (f(a) + f(b));
for (int k = 1; k < n; k++) {
double x = a + k * h;
result += h * f(x);
}
return result;
}
//变步长梯形积分
double T2n(double(*f)(double), double a, double b, double error) {
int n = 1;
double h = (b - a) / n;
double Tn = (f(a) + f(b)) * h / 2.0; //计算 n=1 时的积分,粗略值
double T2n; //步长变为一半后的积分值
bool key = false;
do { //至少循环一次
double Hn = 0.0;
for (int k = 0; k < n; k++) {
double x = a + (k + 0.5) * h;
Hn += h * f(x);
}
T2n = (Tn + Hn) / 2.0;
//判断误差
if (fabs(Tn - T2n) < error) {
key = true;
}
else {
Tn = T2n;
n *= 2;
h /= 2;
}
} while (!key);
return T2n;
}
//复化辛普森公式
double Sn(double(*f)(double), double a, double b) {
int n;
cout << "正在使用复化辛普森公式,请输入分段个数n, 要求为偶数。 n =";
cin >> n;
/*cout << endl;*/
while (n % 2) {
cout << "输入n要求为偶数,请重新输入, n = ";
cin >> n;
cout << endl;
}
double result = 0.0;
double h = (b - a) / n;
result = h / 3.0 * (f(a) + f(b));
for (int k = 1; k < n; k++) {
double x = a + k * h;
if (k % 2 == 0) {
result += h / 3.0 * 2 * f(x);
}
else {
result += h / 3.0 * 4 * f(x);
}
}
return result;
}
2、matlab实现
matlab中自带了函数,例如,  函数、
函数、 函数。
函数。