三次样条函数插值(Cubic spline function interpolation)
Part I 插值
预备知识: 什么是插值?
已知部分离散的数据,但不知道满足这些数据的函数表达式,插值(和拟合)都是为了找到对应的函数表达式。区别在于,插值函数能够穿过已知点,拟合只求函数图形神似而不求穿过已知点。
所谓插值,就是要根据已知点的数值,去计算未知点的数值。下面我非常简略的列出来一些常见的插值方法。
假设我们有这样如下列表,它给出了某个未知函数的一些已知点(事实上这些已知点来自于对一段正弦函数的采样):


要想知道 x=2.5 时的值,我们需要找到一个插值函数,使得这个函数在未知点上插出来的值更准确,更合理,更加接近真实值。
例如:
1,最近邻域插值 ---> f(2.5) = 0.2305
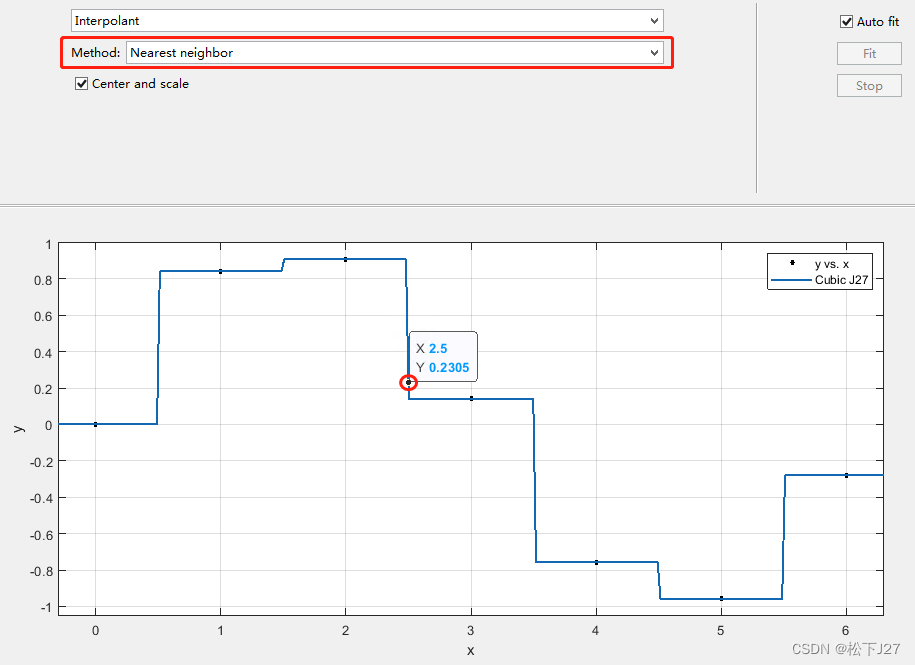
2,线性插值 ---> f(2.5) = 0.5251

3,多项式插值
3阶: 函数不过所有的数据点,f(2.5) = 0.501


4阶: 函数不过所有的数据点,f(2.5) = 0.5306


5阶:当多项式的阶数达到5阶后,函数过所有的数据点,f(2.5) = 0.5954


6阶:函数过所有的数据点,f(2.5) = 0.5964
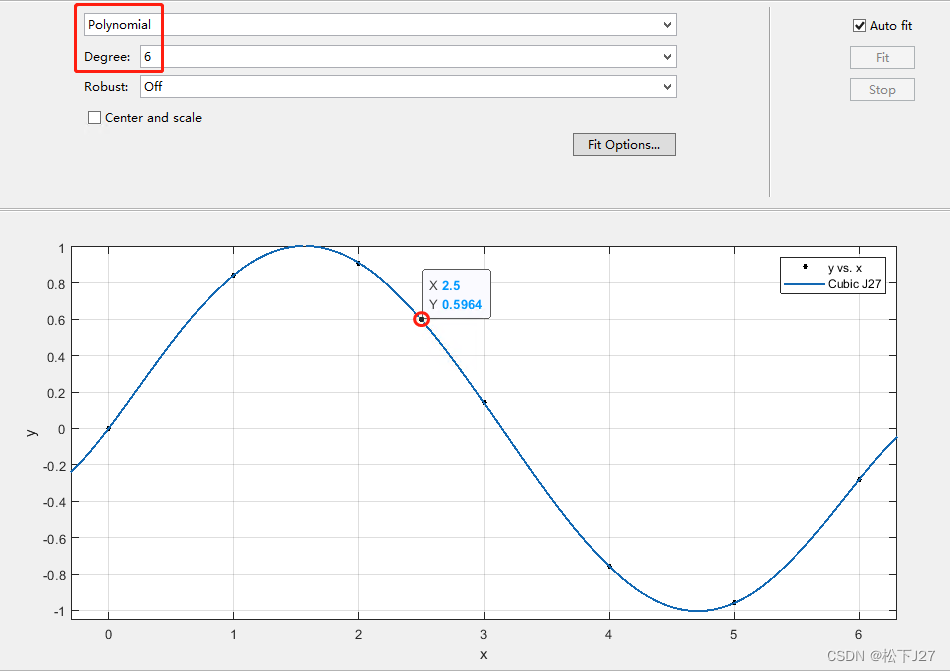

如果我们继续增加多项式的阶数呢?数据不够了!
前面我们求解6阶多项式系数的时候,正好是7个未知数,7个方程,现在我们要求解的7阶多项式有8个未知数呢。
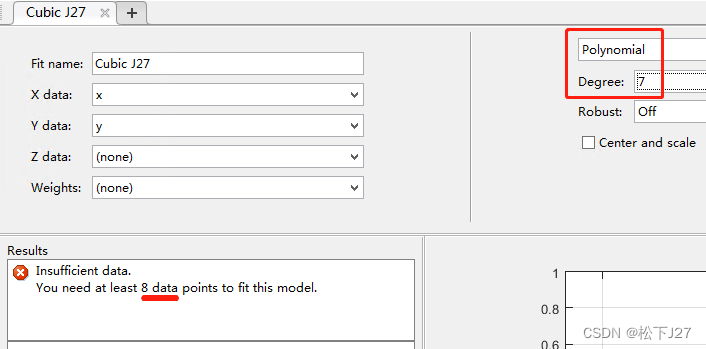
根据上面的实验,我们看到,从最近邻域插值,到线性插值,再到多项式插值(5阶和6阶),都穿过了所有已知点,且插值精度越来越高,越来越合理。但,多项式插值会有两个问题。
1,随着多项式的阶数越来越高,计算量也越来越大。
2,随着多项式的阶数越来越高,插值精度并不会越来越高,恰恰相反,函数曲线会出现剧烈的振荡,即,龙格现象。
PS:龙格现象(Runge)
1901年,Carl David Tolmé Runge意外地发现,用差值插值多项式逼近函数f(x)=1/(1+25x^2)时出现了一些反常的现象。如图,灰色的粗线就是Runge函数在[-1,1]上的图象。蓝色虚线是过[-1,1]上的6个等距点所得到的5次多项式,红色虚线是过[-1,1]上的10个等距点所得到的9次多项式。可以看到,当次数变高时,插值多项式反而变得更不准确。

事实上,当次数n趋于无穷时,该区间上的最大误差值也将趋于无穷大!

插值仿真部分的Matlab code:
%% Author:J27
%% 2022/08/24
x=0:6;
y=[0 0.8415 0.9093 0.1411 -0.7568 -0.9589 -0.2794];
cftool
弹出cf toolbox以后,需手动选择对应的x data和y data.
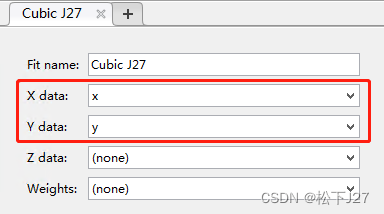
Part II Spline样条函数的出现
什么样的插值函数,既能穿过所有已知点又能避免龙格现象(剧烈的震荡)呢?
答案是,用分段函数插值。就是把所有的已知数据分割成若干段,每段都对应一个插值函数,最终得到一个插值函数序列。
还有,分段函数之间彼此衔接不好怎么办?
答案是,高次样条差值。既每个分段函数都采用高次函数形式来构造(三次样条差值 就是用x的三次方形式构造)这就保证了多个函数之间的衔接光滑。(注:不能用过高阶的函数,否则抖动太剧烈。)


PS:样条一词的由来
“样条”这个词来自于工业绘图时所使用的一种仪器,他是一个细的,可弯曲的木制或塑料工具,固定于给定的数据点上,从而定义出一条“穿过”每一个给定数据点的光滑曲线。

样条的英语单词spline来源于可变形的样条工具,那是一种在造船和工程制图时用来画出光滑形状的工具。在中国大陆,早期曾经被称做「齿函数」。后来因为工程学术语中「放样」一词而得名。
小结:
三次样条插值就是把已知数据分割成若干段,每段构造一个三次函数,并且保证每段三次函数的衔接处具有0阶连续,一阶导数连续,二阶导数连续的性质(也就是光滑衔接)。
Part III 样条函数的数学基本原理
已知n+1个数据节点,分成n个区间(也就是下图中的interval),在每个区间构造一个三次函数,共n段三次函数, ~
~  。注意:下图只是一个示例图,并不跟我后文中所给出的方程组严格对应。
。注意:下图只是一个示例图,并不跟我后文中所给出的方程组严格对应。

假设我们每一段三次函数都用如下的方程来定义:

那么n个区间对应的三次函数S(x)的数学表达式如下:

每段三次函数S(x)都有a,b,c,d四个系数(即:未知数),上述n段三次函数,共有4xn个系数(未知数)。要想求解这4n个未知数,共需要4n个方程。这就好比,我要求解y=ax+b中的两个系数(未知数)a,b,我们至少要知道两个点p1(x1,y1)和p2(x2,y2),联立两个方程y1=ax1+b和y2=ax2+b,才能求出系数a,b一样。
下面,我们根据三次样条函数对每一段三次函数在断点处的约束(期望),生成求解4n个系数a,b,c,d所需的所有方程。
条件1:n段三次函数必须穿过所有已知节点


已知n+1个数据节点,要让n段函数三次函数穿过所有的数据点,总共可以生成n+1个方程。其中,前n个方程由i=0~n-1给出,第n+1个方程,由i=n单独给出)

前n个方程所表达的实际意义是,S0~Sn-1段函数必定会经过自己所在区间的起点,例如,点(x0,y0) for S0(x)。而,最后一个方程所描述的是Sn-1段函数,也就是最后一段函数必定会过自己所在区间的终点(xn,yn)。简而言之就是,前面n-1段函数保证过起点,而最后一段函数,即过起点也过终点。
条件2:在所有节点(除了第一节点和最后一个节点)处0阶连续(保证数据不间断,无跳变),即,前一段方程在节点处的函数值和后一段方程在相同节点处的函数值相等。

其中,i=0,1,2…n-2(共得到n-1个方程,因为n段三次函数之间共有n-1的衔接点)
(注:根据条件一可推导出 ,也就是前面说的过终点)
,也就是前面说的过终点)

Tips:
0阶导数连续的函数举例

0阶导数不连续的函数举例

上图中的函数在x=1处是没有定义的
条件3:在所有节点(除了第一节点和最后一个节点)处1阶连续(保证节点处有相同的斜率,原函数曲线上没有剧烈的跳变)

i= 0,1,2…n-2 (共得到n-1个方程,n段三次函数之间共有n-1的衔接点)
Tips:
1.函数在某一点"有极限"等价于左极限=右极限
2.函数在某一点"连续"等价于左极限=右极限=函数值

一阶导数函数不连续的函数举例:

一阶导数函数连续的函数举例:

换句话说:保证S'(x)的一阶连续意味着曲线y=S(x)没有急转弯,没有特别剧烈的跳变。
条件4:在所有节点(除了第一节点和最后一个节点)处2阶连续(保证节点处有相同的曲率,即,相同的弯曲程度)

i= 0,1,2…n-2 (共n-1个方程,n段三次函数之间共有n-1的衔接点)
或者说:保证S''(x)的连续,意味着每个点的曲率半径有定义(其实我也不懂什么叫曲率半径,哈哈)。
综上,第一个约束条件得到了n+1个方程,第二,三,四个约束条件分别得到n-1个方程,共4n-2个方程,还差2个方程。(最后缺少的这两个方程,会在后面给出)
Part IV 求解方程组
先分别求出函数S(x)的一阶导数和二阶导数
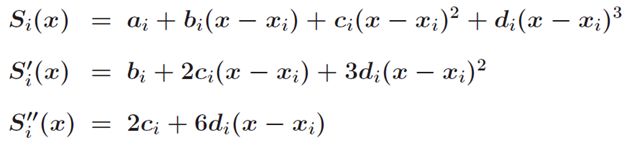

根据条件1 推导出:
推导出:
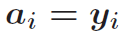

根据条件2 ,(即
,(即 )推导出:
)推导出:
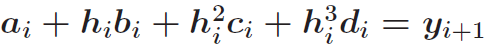

根据条件3 推导出:
推导出:
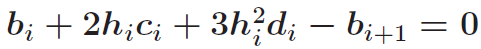

根据条件4  推导出:
推导出:
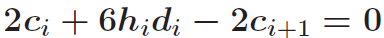

令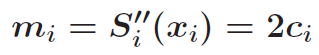 可得:
可得:
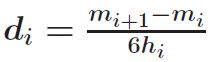

后续推导:
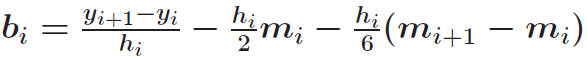

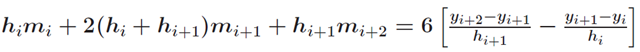

Part V 端点条件(最后增加两个约束条件,使得方程组数目正好是4n)
1,自由边界(Natural)
Natural样条是柔软又有弹性的木杆经过所有数据点后形成的曲线,让端点的斜率自由的在某一位置保持平衡,使得曲线的摇摆最小。
自由边界的两个附加边界条件:

推导过程:


自由边界生成的线性方程组:



2,固定边界/紧压样条(Clamped)
紧压样条在端点有固定的斜率。紧压样条可想象为,用外力使柔软而有弹性得木杆经过数据点,并在端点处使其具有固定得斜率。这样的样条对于画经过多个点的光滑曲线的绘图员相当有用。
紧压样条的两个附加边界条件:
 ,
,
简而言之,就是指定第一段函数 在左起第一个点
在左起第一个点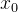 处的斜率为A,最后一段函数
处的斜率为A,最后一段函数 在右端最后一个点
在右端最后一个点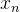 处的斜率为B。
处的斜率为B。
推导过程:



紧压样条生成的线性方程组:



3,非节点边界(Not-A-Knot)
非节点边界要求第一段S0和第二段S1三次函数在第二个数据点X1处三阶导数连续,同时也要求倒数第二段Sn-2和最后一段函数Sn-1在倒数第二个数据点Xn-1处三阶导数连续。(也就是说,整个样条函数中,前两段函数完全相同,最后两段的函数也完全相同。同时,0阶,1阶,2阶,3阶全都连续保证了数据点两端的参数a,b,c,d都相同。)
非节点边界的两个附加边界条件:
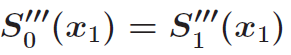
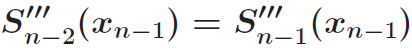
推导过程:


非节点边界生成的线性方程组:



(全文完)
作者 --- 松下J27
参考文献(鸣谢):
1,Thomas' Calculus (12th Edition) -Addison Wesley
2,托马斯微积分
3,作者:Winters 链接:https://www.zhihu.com/question/31269601/answer/244310086 来源:知乎
4, 三次样条插值(Cubic Spline Interpolation)及代码实现(C语言) - 马语者 - 博客园
5, Runge现象:多项式插值不见得次数越高越准确 | Matrix67: The Aha Moments
之前写的有些问题,现在已经做了修订。2021/03/22
关于插值部分做了一些补充。2021/10/29
对部分方程的具体意义做了说明。2022/05/20晚
修改了文章开头部分的插值部分的插图和说明,并增加了相应的Matlab code。 2022/08/24
又改了改。 2023/02/02
格言摘抄:
不轻易发怒的,胜过勇士;治服己心的,强如取城。签放在怀里,定事由耶和华。 (《圣经》箴言 16章32-33节)

(配图与本文无关)
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27