包含相同内容的两幅图像可能由于成像角度,透视关系乃至镜头自身原因所造成的几何失真而呈现截然不同的外观。
通过适当的几何变换可以最大程度地消除这些几何失真所产生的负面影响,有利于在后续的处理和识别工作中将注意力集中于图像的内容本身。
一个几何变换需要两部分运算:
首先是空间变换所需的运算,如平移、旋转和镜像等,需要用它来表示输出图像与输入图像之间的映射关系;
此外,还需要使用灰度插值算法,按照这种变换关系进行计算,输出图像的像素可能被映射到输入图像的非整数坐标上。
设原图像
f
(
x
0
,
y
0
)
f(x_0, y_0)
f(x0,y0)经过几何变换产生的目标图像为
g
(
x
1
,
y
1
)
g(x_1, y_1)
g(x1,y1),则该空间变换映射关系可表示为:
x
1
=
s
(
x
0
,
y
0
)
(1)
x_1 = s(x_0, y_0) \tag{1}
x1=s(x0,y0)(1)
y 1 = t ( x 0 , y 0 ) (2) y_1 = t(x_0, y_0) \tag{2} y1=t(x0,y0)(2)
其中, s ( x 0 , y 0 ) s(x_0, y_0) s(x0,y0)和 t ( x 0 , y 0 ) t(x_0, y_0) t(x0,y0)为由 f ( x 0 , y 0 ) f(x_0, y_0) f(x0,y0)到 g ( x 1 , y 1 ) g(x_1, y_1) g(x1,y1)的坐标变换函数。
比如,当 x 1 = s ( x 0 , y 0 ) = 2 x 0 x_1 = s(x_0, y_0) = 2 x_0 x1=s(x0,y0)=2x0, y 1 = t ( x 0 , y 0 ) = 2 y 0 y_1 = t(x_0, y_0) = 2 y_0 y1=t(x0,y0)=2y0时,变换后的图像 g ( x 1 , y 1 ) g(x_1, y_1) g(x1,y1)只是简单地在 x x x和 y y y两个空间方向上将 f ( x 0 , y 0 ) f(x_0, y_0) f(x0,y0)的尺寸放大一倍。
掌握了有关变换函数 s ( x 0 , y 0 ) s(x_0, y_0) s(x0,y0)和 t ( x 0 , y 0 ) t(x_0, y_0) t(x0,y0)的情况,可以遵循下面的步骤实现几何变换。
算法4.1步骤:
对于几何失真图像的复原(校正)过程正好是上述变换的逆过程。
x
0
=
s
−
1
(
x
1
,
y
1
)
(3)
x_0 = s^{-1} (x_1, y_1) \tag{3}
x0=s−1(x1,y1)(3)
y 0 = t − 1 ( x 1 , y 1 ) (4) y_0 = t^{-1}(x_1, y_1) \tag{4} y0=t−1(x1,y1)(4)
式(3)和(4)表示相应的由 g ( x 1 , y 1 ) g(x_1, y_1) g(x1,y1)到 f ( x 0 , y 0 ) f(x_0, y_0) f(x0,y0)的逆变换。此时,经过几何变换而失真的图像 g ( x 1 , y 1 ) g(x_1, y_1) g(x1,y1)是要复原的对象,原始图像 f ( x 0 , y 0 ) f(x_0, y_0) f(x0,y0)是复原的目标。
当图像归一化用于消除几何因素造成的图像外观变化时,称为图像几何归一化,它能够排除对象间几何关系的差别,找出图像中的那些几何不变量,从而得知这些对象原本就是一样的或属于相同的类别。
图像平移就是将图像中所有的点按照指定的平移量水平或垂直移动。
设
(
x
0
,
y
0
)
(x_0, y_0)
(x0,y0)是原图像上的一点,图像水平平移量为
T
x
T_x
Tx, 垂直平移量为
T
y
T_y
Ty,
平移之后的点坐标变为
(
x
1
,
y
1
)
(x_1, y_1)
(x1,y1),变为
x
1
=
x
0
+
t
x
x_1 = x_0 + t_x
x1=x0+tx
y
1
=
y
0
+
t
y
y_1 = y_0 + t_y
y1=y0+ty
用矩阵表示为
[
x
1
y
1
1
]
=
[
x
0
y
0
1
]
[
1
0
0
0
1
0
T
x
T
y
1
]
(5)
\begin{bmatrix} x_1 & y_1 & 1 \end{bmatrix} = \begin{bmatrix} x_0 & y_0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ T_x & T_y & 1 \end{bmatrix} \tag{5}
[x1y11]=[x0y01]
10Tx01Ty001
(5)
对变换矩阵求逆,可以得到逆变换:
[
x
0
y
0
1
]
=
[
x
1
y
1
1
]
[
1
0
0
0
1
0
−
T
x
−
T
y
1
]
(6)
\begin{bmatrix} x_0 & y_0 & 1 \end{bmatrix} = \begin{bmatrix}x_1 & y_1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -T_x & - T_y & 1 \end{bmatrix} \tag{6}
[x0y01]=[x1y11]
10−Tx01−Ty001
(6)
即
{
x
0
=
x
1
−
T
x
y
0
=
y
1
−
T
y
(7)
\left \{ \begin{matrix} x_0 = x_1 - T_x \\ y_0 = y_1 - T_y \end{matrix} \right. \tag{7}
{x0=x1−Txy0=y1−Ty(7)
从上面的公式中可以得到,平移后的目标图像中的每一点都可以在原图像中找到对应的点。
比如,对于新图中的 ( i , j ) (i,j) (i,j)像素,带入公式可以得到其对应原图像中的像素 ( i − T x , j − T y ) (i-T_x, j-T_y) (i−Tx,j−Ty)。此时,如果 T x > i T_x > i Tx>i 或 T y > j T_y > j Ty>j,点 ( i − T x , j − T y ) (i-T_x, j-T_y) (i−Tx,j−Ty)就超出了原图的范围,可以直接将它的像素值统一设置为 0 0 0或 255 255 255。
对于原图中被移出图像显示区域的点通常也有两种处理方法,可以直接丢弃,也可以通过适当增加目标图像的尺寸,将新生成的图像宽度增加 T x T_x Tx,高度增加 T y T_y Ty的方法使得新图像中能够包含这些点。
imtransform函数用于完成一般的二维空间变换。
函数原型:B = imtransform(A, TFORM, method);
可以通过两种方法来创建TFORM结构,使用maketform函数和cp2tform函数。
cp2tform是一个数据拟合函数,它需要原图像与目标图像之间的对应点对作为输入,用于确定基于控制点对的几何变换关系。
maketform函数调用形式:T = maketform(transformtype, Matrix);
图像镜像变换分为水平镜像和垂直镜像。水平镜像将图像左半部分和右半部分以图像竖直中轴线为中心轴进行兑换;竖直镜像将图像上半部分和下半部分以图像水平中轴线为中心轴进行兑换。
水平镜像的变换公式:
[
x
1
y
1
1
]
=
[
x
0
y
0
1
]
[
−
1
0
0
0
1
0
W
i
d
t
h
0
1
]
=
[
W
i
d
t
h
−
x
0
y
0
1
]
(8)
\begin{bmatrix} x_1 & y_1 & 1 \end{bmatrix} = \begin{bmatrix} x_0 & y_0 & 1 \end{bmatrix} \begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ Width & 0 & 1 \end{bmatrix} = \begin{bmatrix}Width-x_0 & y_0 & 1 \end{bmatrix} \tag{8}
[x1y11]=[x0y01]
−10Width010001
=[Width−x0y01](8)
对矩阵求逆得到:
[
x
0
y
0
1
]
=
[
x
1
y
1
1
]
[
−
1
0
0
0
1
0
W
i
d
t
h
0
1
]
=
[
W
i
d
t
h
−
x
1
y
1
1
]
(9)
\begin{bmatrix} x_0 & y_0 & 1 \end{bmatrix} = \begin{bmatrix} x_1 & y_1 & 1 \end{bmatrix} \begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ Width & 0 & 1 \end{bmatrix} = \begin{bmatrix} Width - x_1 & y_1 & 1 \end{bmatrix} \tag{9}
[x0y01]=[x1y11]
−10Width010001
=[Width−x1y11](9)
竖直镜像变换关系可形式化地描述如下:
[
x
1
y
1
1
]
=
[
x
0
y
0
1
]
[
1
0
0
0
−
1
0
0
H
e
i
g
h
t
1
]
(10)
\begin{bmatrix}x_1 & y_1 & 1 \end{bmatrix} = \begin{bmatrix} x_0 & y_0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & Height & 1 \end{bmatrix} \tag{10}
[x1y11]=[x0y01]
1000−1Height001
(10)
逆运算为:
[
x
0
y
0
1
]
=
[
x
1
y
1
1
]
[
1
0
0
0
−
1
0
0
H
e
i
g
h
t
1
]
(11)
\begin{bmatrix}x_0 & y_0 & 1 \end{bmatrix} = \begin{bmatrix}x_1 & y_1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & Height & 1 \end{bmatrix} \tag{11}
[x0y01]=[x1y11]
1000−1Height001
(11)
图像转置是将图像像素的 x x x坐标和 y y y坐标互换,转置后图像的大小会随之改变,高度和宽度将互换。
转置变换公式如下:
[
x
1
y
1
1
]
=
[
x
0
y
0
1
]
[
0
1
0
1
0
0
0
0
1
]
(12)
\begin{bmatrix}x_1 & y_1 & 1 \end{bmatrix} = \begin{bmatrix}x_0 & y_0 & 1 \end{bmatrix} \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix} \tag{12}
[x1y11]=[x0y01]
010100001
(12)
转置矩阵的逆矩阵仍然为其自身。
图像缩放是指图像按照指定的比率放大或者缩小。
假设图像
x
x
x轴方向的缩放比率为
S
x
S_x
Sx,
y
y
y轴方向的缩放比率为
S
y
S_y
Sy,相应的变换表达式为:
[
x
1
y
1
1
]
=
[
x
0
y
0
1
]
[
S
x
0
0
0
S
y
0
0
0
1
]
=
[
x
0
⋅
S
x
y
0
⋅
S
y
1
]
(13)
\begin{bmatrix} x_1 & y_1 & 1 \end{bmatrix} = \begin{bmatrix} x_0 & y_0 & 1 \end{bmatrix} \begin{bmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix}x_0 \cdot S_x & y_0 \cdot S_y & 1 \end{bmatrix} \tag{13}
[x1y11]=[x0y01]
Sx000Sy0001
=[x0⋅Sxy0⋅Sy1](13)
其逆运算如下:
[
x
0
y
0
1
]
=
[
x
1
y
1
1
]
[
1
S
x
0
0
0
1
S
y
0
0
0
1
]
=
[
x
1
S
x
y
1
S
y
1
]
(14)
\begin{bmatrix} x_0 & y_0 & 1 \end{bmatrix} = \begin{bmatrix} x_1 & y_1 & 1 \end{bmatrix} \begin{bmatrix} \frac{1}{S_x} & 0 & 0 \\ 0 & \frac{1}{S_y} & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} \frac{x_1}{S_x} & \frac{y_1}{S_y} & 1 \end{bmatrix} \tag{14}
[x0y01]=[x1y11]
Sx1000Sy10001
=[Sxx1Syy11](14)
直接根据缩放公式计算得到的目标图像,某些映射源坐标可能不是整数,从而找不到对应的像素位置。比如当图像放大2倍时,即
S
x
=
S
y
=
2
S_x = S_y = 2
Sx=Sy=2,放大图像中的像素
(
0
,
1
)
(0,1)
(0,1)对应于原图中的像素
(
0
,
0.5
)
(0, 0.5)
(0,0.5),这不是整数坐标位置,无法提取其灰度值。
必须进行某种近似处理,一种简单的策略是直接使用最邻近的整数坐标位置 ( 0 , 0 ) (0,0) (0,0)或者 ( 0 , 1 ) (0,1) (0,1)处的像素灰度值,这也是最近邻插值算法。
旋转一般是指将图像围绕某一指定点旋转一定的角度。旋转通常也会改变图像的大小。如下图所示
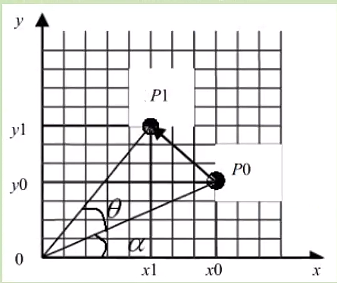
点 P ( x 0 , y 0 ) P(x_0, y_0) P(x0,y0)绕原点逆时针旋转角度 θ \theta θ到 P 1 ( x 1 , y 1 ) P1(x_1, y_1) P1(x1,y1),令 L = ∣ O P ∣ = x 2 + y 2 L = |OP| = \sqrt{x^2 + y^2} L=∣OP∣=x2+y2 ,有: s i n α = y 0 / L sin \alpha = y_0/L sinα=y0/L, c o s α = x 0 / L cos \alpha = x_0/L cosα=x0/L。
到达
P
1
P1
P1点后,有:
s
i
n
(
α
+
θ
)
=
y
1
/
L
=
c
o
s
θ
s
i
n
α
+
s
i
n
θ
c
o
s
α
c
o
s
(
α
+
θ
)
=
x
1
/
L
=
c
o
s
θ
c
o
s
α
−
s
i
n
θ
s
i
n
α
(15)
sin(\alpha + \theta) = y_1 / L = cos \theta sin \alpha + sin \theta cos \alpha \tag{15} \\ cos(\alpha + \theta) = x_1/L = cos \theta cos \alpha - sin \theta sin \alpha
sin(α+θ)=y1/L=cosθsinα+sinθcosαcos(α+θ)=x1/L=cosθcosα−sinθsinα(15)
于是有:
x
1
=
c
o
s
θ
x
0
−
s
i
n
θ
y
0
y
1
=
c
o
s
θ
y
0
+
s
i
n
θ
x
0
(16)
x_1 = cos \theta x_0 - sin \theta y_0 \tag{16} \\ y_1 = cos \theta y_0 +sin \theta x_0
x1=cosθx0−sinθy0y1=cosθy0+sinθx0(16)
得到旋转变换公式为:
[
x
1
y
1
1
]
=
[
x
0
y
0
1
]
[
c
o
s
θ
s
i
n
θ
0
−
s
i
n
θ
c
o
s
θ
0
0
0
1
]
(17)
\begin{bmatrix} x_1 & y_1 & 1 \end{bmatrix} = \begin{bmatrix} x_0 & y_0 & 1 \end{bmatrix} \begin{bmatrix} cos \theta & sin \theta & 0 \\ -sin \theta & cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \tag{17}
[x1y11]=[x0y01]
cosθ−sinθ0sinθcosθ0001
(17)
其逆运算为:
[
x
0
y
0
1
]
=
[
x
1
y
1
1
]
[
c
o
s
θ
−
s
i
n
θ
0
s
i
n
θ
c
o
s
θ
0
0
0
1
]
(18)
\begin{bmatrix} x_0 & y_0 & 1 \end{bmatrix} = \begin{bmatrix} x_1 & y_1 & 1 \end{bmatrix} \begin{bmatrix} cos \theta & - sin \theta & 0 \\ sin \theta & cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \tag{18}
[x0y01]=[x1y11]
cosθsinθ0−sinθcosθ0001
(18)
上面的讨论基于以原点即图像左下角为中心进行的,如何围绕任意的指定点来旋转?
将平移和旋转操作相结合即可,先进行坐标系平移,再以新的坐标原点为中心旋转,之后将新原点平移回原坐标系的原点。这个过程可以归纳为以下3个步骤:
以围绕图像中心的旋转为例,如下图所示,坐标系Ⅰ以图像左上角点位原点,向右为 x x x轴正方向,向下为 y y y轴正方向;而坐标系Ⅱ以图像中心为原点,向右为 x x x轴正方向,向下为 y y y轴正方向。坐标系Ⅰ与坐标系Ⅱ之间的转换关系如下:
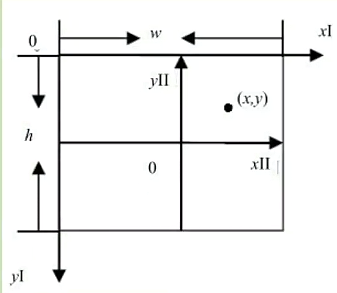
假设图像的宽为
w
w
w, 高位
h
h
h,容易得到:
[
x
Ⅰ
y
Ⅰ
1
]
=
[
x
Ⅱ
y
Ⅱ
1
]
[
1
0
0
0
−
1
0
0.5
w
0.5
h
1
]
(19)
\begin {bmatrix} x_Ⅰ \\ y_Ⅰ \\ 1 \end{bmatrix} = \begin {bmatrix} x_Ⅱ \\ y_Ⅱ \\ 1 \end{bmatrix} \begin {bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0.5w & 0.5h & 1 \end{bmatrix} \tag{19}
xⅠyⅠ1
=
xⅡyⅡ1
100.5w0−10.5h001
(19)
相应的逆变换为:
[
x
Ⅱ
y
Ⅱ
1
]
=
[
x
Ⅰ
y
Ⅰ
1
]
[
1
0
0
0
−
1
0
−
0.5
w
0.5
h
1
]
(20)
\begin{bmatrix} x_Ⅱ \\ y_Ⅱ \\ 1 \end{bmatrix} = \begin{bmatrix} x_Ⅰ \\ y_Ⅰ \\ 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ -0.5w & 0.5h & 1 \end{bmatrix} \tag{20}
xⅡyⅡ1
=
xⅠyⅠ1
10−0.5w0−10.5h001
(20)
这里已经实现上述3个步骤中的第1步和第3步,再加上第2步的旋转变换就得到了围绕图像中心点旋转的最终变换矩阵。该矩阵实际上是3个变换步骤中分别用到的3个变换矩阵的级联。式中,
W
o
l
d
W_{old}
Wold、
H
o
l
d
H_{old}
Hold、
W
n
e
w
W_{new}
Wnew、
H
n
e
w
H_{new}
Hnew分别表示原图像和新图像的宽和高。
[ x 1 y 1 1 ] = [ x 0 y 0 1 ] [ 1 0 0 0 − 1 0 − 0.5 W o l d 0.5 H o l d 1 ] [ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] [ 1 0 0 0 − 1 0 0.5 W n e w 0.5 H n e w 1 ] = [ x 0 y 0 1 ] [ c o s θ s i n θ 0 − s i n θ c o s θ 0 0.5 ⋅ ( − W o l d ⋅ c o s θ + H o l d ⋅ s i n θ + W n e w ) 0.5 ( − W o l d ⋅ s i n θ − H o l d ⋅ c o s θ + H n e w ) 1 ] \begin{align} \begin{bmatrix} x_1 \\ y_1 \\ 1 \end{bmatrix} &= \begin{bmatrix} x_0 \\ y_0 \\ 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ -0.5W_{old} & 0.5H_{old} & 1 \end{bmatrix} \begin{bmatrix} cos \theta & -sin \theta & 0 \\ sin \theta & cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0.5W_{new} & 0.5 H_{new} & 1 \end{bmatrix} \nonumber \\ &= \begin{bmatrix} x_0 \\ y_0 \\ 1 \end{bmatrix} \begin{bmatrix} cos \theta & sin \theta & 0 \\ -sin \theta & cos \theta & 0 \\ 0.5 \cdot (-W_{old} \cdot cos \theta + H_{old} \cdot sin \theta + W_{new} ) & 0.5 ( - W_{old} \cdot sin \theta - H_{old} \cdot cos \theta + H_{new}) & 1 \end{bmatrix} \tag{21} \end{align} x1y11 = x0y01 10−0.5Wold0−10.5Hold001 cosθsinθ0−sinθcosθ0001 100.5Wnew0−10.5Hnew001 = x0y01 cosθ−sinθ0.5⋅(−Wold⋅cosθ+Hold⋅sinθ+Wnew)sinθcosθ0.5(−Wold⋅sinθ−Hold⋅cosθ+Hnew)001 (21)
上式的逆变换为:
[ x 0 y 0 1 ] = [ x 1 y 1 1 ] [ 1 0 0 0 − 1 0 − 0.5 W n e w 0.5 H n e w 1 ] [ c o s θ s i n θ 0 − s i n θ c o s θ 0 0 0 1 ] [ 1 0 0 0 − 1 0 0.5 W o l d 0.5 H o l d 1 ] = [ x 1 y 1 1 ] [ c o s θ − s i n θ 0 s i n θ c o s θ 0 − 0.5 W n e w ⋅ c o s θ − 0.5 H n e w ⋅ s i n θ + 0.5 W o l d 0.5 W n e w ⋅ s i n θ − 0.5 H n e w ⋅ c o s θ + 0.5 H o l d 1 ] \begin{align} \begin{bmatrix} x_0 \\ y_0 \\ 1 \end{bmatrix} &= \begin{bmatrix} x_1 \\ y_1 \\ 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ -0.5W_{new} & 0.5 H_{new} & 1 \end{bmatrix} \begin{bmatrix} cos \theta & sin \theta & 0 \\ -sin \theta & cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0.5W_{old} & 0.5 H_{old} & 1 \end{bmatrix} \nonumber \\ &= \begin{bmatrix} x_1 \\ y_1 \\ 1 \end{bmatrix} \begin{bmatrix} cos \theta & -sin \theta & 0 \\ sin \theta & cos \theta & 0 \\ -0.5 W_{new} \cdot cos \theta - 0.5 H_{new} \cdot sin \theta + 0.5 W_{old} & 0.5 W_{new} \cdot sin \theta - 0.5 H_{new} \cdot cos \theta + 0.5 H_{old} & 1 \end{bmatrix} \tag{22} \end{align} x0y01 = x1y11 10−0.5Wnew0−10.5Hnew001 cosθ−sinθ0sinθcosθ0001 100.5Wold0−10.5Hold001 = x1y11 cosθsinθ−0.5Wnew⋅cosθ−0.5Hnew⋅sinθ+0.5Wold−sinθcosθ0.5Wnew⋅sinθ−0.5Hnew⋅cosθ+0.5Hold001 (22)
可以根据逆变换公式,按照算法4.1中的描述实现围绕图像中心的旋转变换,类似地,可以进一步得到以任意点为中心的旋转变换。
实现几何运算时,有两种方法:向前映射法和向后映射法。
常用的插值算法有:最近邻插值、双线性插值、高阶插值。
最近邻插值算法,输出像素的值为输入图像中与其最邻近的采样点的像素值。
最近邻插值可以表示为
f
(
x
,
y
)
=
g
(
r
o
u
n
d
(
x
)
,
r
o
u
n
d
(
y
)
)
(23)
f(x,y) = g(round(x), round(y)) \tag{23}
f(x,y)=g(round(x),round(y))(23)
最近邻插值计算简单,在多数情况下的输出效果也可以接收。但是,最近邻插值会在图像中产生人为加工的痕迹。
双线性插值又称为一阶插值,是线性插值扩展到二维的一种应用,可以通过一系列的一阶线性插值得到。
线性,指量与量之间按比例、成直线的关系,在数学上可以理解为一阶导数为常数的函数。
线性插值是指根据两个点的值线性地确定位于这两个点连线上的某一点的值。
输出像素的值为输入图像中距离它最近的 2 × 2 2 \times 2 2×2邻域内采样点像素灰度值的加权平均。
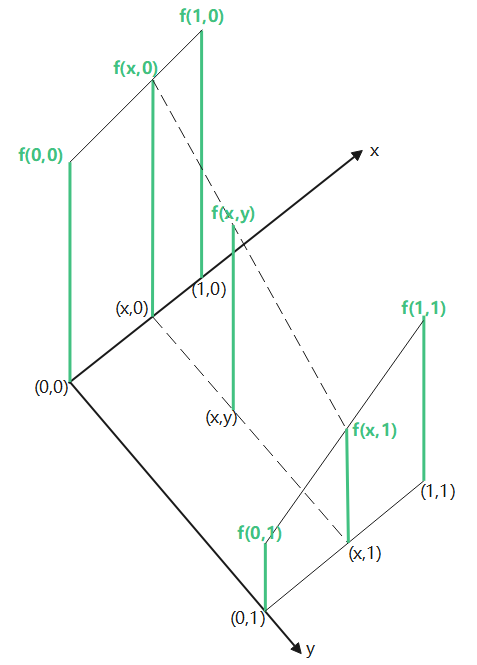
设已知单位正方形的顶点坐标分别为 f ( 0 , 0 ) , f ( 1 , 0 ) , f ( 0 , 1 ) , f ( 1 , 1 ) f(0,0), f(1,0), f(0,1), f(1,1) f(0,0),f(1,0),f(0,1),f(1,1),如下图所示,要通过线性插值得到正方形内任意点 f ( x , y ) f(x,y) f(x,y)的值。
首先对上端的两个点进行线性插值,得到 f ( x , 0 ) f(x,0) f(x,0): f ( x , 0 ) = f ( 0 , 0 ) + x [ f ( 1 , 0 ) − f ( 0 , 0 ) ] f(x,0) = f(0,0) + x [f(1,0) - f(0,0)] f(x,0)=f(0,0)+x[f(1,0)−f(0,0)];
再对下端的两个顶点进行线性插值,得到 f ( x , 1 ) f(x,1) f(x,1): f ( x , 1 ) = f ( 0 , 1 ) + x [ f ( 1 , 1 , ) − f ( 0 , 1 ) ] f(x,1) = f(0,1) + x[f(1,1,) - f(0,1)] f(x,1)=f(0,1)+x[f(1,1,)−f(0,1)];
最后,对垂直方向进行线性插值,得到 f ( x , y ) f(x,y) f(x,y): f ( x , y ) = f ( x , 0 ) + y [ f ( x , 1 ) − f ( x , 0 ) ] f(x,y) = f(x,0) + y [f(x,1) - f(x,0)] f(x,y)=f(x,0)+y[f(x,1)−f(x,0)];
整理得到 f ( x , y ) f(x,y) f(x,y):
f ( x , y ) = [ f ( 1 , 0 ) − f ( 0 , 0 ) ] x + [ f ( 0 , 1 ) − f ( 0 , 0 ) ] y + [ f ( 1 , 1 ) + f ( 0 , 0 ) − f ( 0 , 1 ) − f ( 1 , 0 ) ] x y + f ( 0 , 0 ) (24) f(x,y) = [f(1,0) - f(0,0)] x + [f(0,1) - f(0,0)]y + [f(1,1) + f(0,0) - f(0,1) - f(1,0)] xy + f(0,0) \tag{24} f(x,y)=[f(1,0)−f(0,0)]x+[f(0,1)−f(0,0)]y+[f(1,1)+f(0,0)−f(0,1)−f(1,0)]xy+f(0,0)(24)
双线性插值的平滑作用会使图像的细节退化,而其斜率的不连续性则会导致变换产生不希望的结果。
双线性插值的去热点可以通过高阶插值得到弥补,高阶插值通常用卷积来实现。
输出像素的值为输入图像中距离它最近的 4 × 4 4 \times 4 4×4邻域内采样点像素值的加权平均值。
以三次插值为例,它使用了如下的三次多项式来逼近理论上的最佳插值函数
s
i
n
c
(
x
)
sinc(x)
sinc(x)。
S
(
x
)
=
{
1
−
2
∣
x
∣
2
+
∣
x
∣
3
,
0
≤
∣
x
∣
<
1
4
−
8
∣
x
∣
+
5
∣
x
∣
2
−
∣
x
∣
3
,
1
≤
∣
x
∣
<
2
0
∣
x
∣
≥
2
(25)
S(x) = \left \{ \begin{matrix} \tag{25} 1 - 2 |x|^2 + |x|^3 , & 0 \le | x| < 1 \\ 4 - 8 |x| + 5 |x|^2 - |x|^3, & 1 \le |x| < 2 \\ 0 & |x| \ge 2 \end{matrix} \right.
S(x)=⎩
⎨
⎧1−2∣x∣2+∣x∣3,4−8∣x∣+5∣x∣2−∣x∣3,00≤∣x∣<11≤∣x∣<2∣x∣≥2(25)
上式中
∣
x
∣
|x|
∣x∣是周围像素沿
x
x
x方向与原点的距离。待求像素
(
x
,
y
)
(x,y)
(x,y)的灰度值由其周围16个点的灰度值加权插值得到。计算公式如下:
f
(
x
,
y
)
=
f
(
i
+
u
,
j
+
v
)
=
A
B
C
(26)
f(x,y) = f(i+u, j+v) = ABC \tag{26}
f(x,y)=f(i+u,j+v)=ABC(26)
其中
A
=
[
S
(
1
+
v
)
S
(
v
)
S
(
1
−
v
)
S
(
2
−
v
)
]
T
C
=
[
S
(
1
+
u
)
S
(
u
)
S
(
1
−
u
)
S
(
2
−
u
)
]
B
=
[
f
(
i
−
1
,
j
−
1
)
f
(
i
−
1
,
j
)
f
(
i
−
1
,
j
+
1
)
f
(
i
−
1
,
j
+
2
)
f
(
i
,
j
−
1
)
f
(
i
,
j
)
f
(
j
,
j
+
1
)
f
(
i
,
j
+
2
)
f
(
i
+
1
,
j
−
1
)
f
(
i
+
1
,
j
)
f
(
i
+
1
,
j
+
1
)
f
(
i
+
1
,
j
+
2
)
f
(
i
+
2
,
j
−
1
)
f
(
i
+
2
,
j
)
f
(
i
+
2
,
j
+
1
)
f
(
i
+
2
,
j
+
2
)
]
A = \begin{bmatrix} S(1+v) \\ S(v) \\ S(1-v) \\ S(2-v) \end{bmatrix} ^T \nonumber \\ C = \begin{bmatrix} S(1+u) \\ S(u) \\ S(1-u) \\ S(2-u) \end{bmatrix} \nonumber \\ B = \begin{bmatrix} f(i-1, j-1) & f(i-1, j) & f(i-1,j+1) & f(i-1, j+2) \nonumber \\ f(i,j-1) & f(i, j) & f(j, j+1) & f(i, j+2) \nonumber \\ f(i+1, j-1) & f(i+1, j) & f(i+1, j+1) & f(i+1, j+2) \nonumber \\ f(i+2, j-1) & f(i+2, j) & f(i+2, j+1) & f(i+2, j+2) \end{bmatrix}
A=
S(1+v)S(v)S(1−v)S(2−v)
TC=
S(1+u)S(u)S(1−u)S(2−u)
B=
f(i−1,j−1)f(i,j−1)f(i+1,j−1)f(i+2,j−1)f(i−1,j)f(i,j)f(i+1,j)f(i+2,j)f(i−1,j+1)f(j,j+1)f(i+1,j+1)f(i+2,j+1)f(i−1,j+2)f(i,j+2)f(i+1,j+2)f(i+2,j+2)
三次插值方法通常应用在光栅显示中,它在允许任意比例的缩放操作的同时,较好地保持了图像的细节。
未完待续~
