计算机图形学中的应用非常广泛的变换是一种称为仿射变换的特殊变换，在仿射变换中的基本变换包括平移、旋转、缩放、剪切这几种。本文以及接下来的几篇文章重点介绍一下关于旋转的变换，包括二维旋转变换、三维旋转变换以及它的一些表达方式（旋转矩阵、四元数、欧拉角等）。
首先要明确旋转在二维中是绕着某一个点进行旋转，三维中是绕着某一个轴进行旋转。二维旋转中最简单的场景是绕着坐标原点进行的旋转，如下图所示：
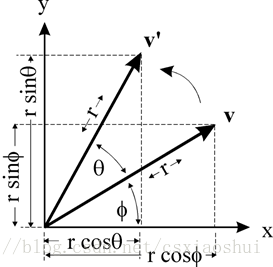
如图所示点v 绕 原点旋转θθ 角，得到点v’，假设 v点的坐标是(x, y) ，那么可以推导得到 v’点的坐标（x’, y’)(设原点到v的距离是r，原点到v点的向量与x轴的夹角是ϕϕ )
x=rcosϕy=rsinϕx=rcosϕy=rsinϕ
x′=rcos(θ+ϕ)y′=rsin(θ+ϕ)x′=rcos(θ+ϕ)y′=rsin(θ+ϕ)
通过三角函数展开得到
x′=rcosθcosϕ−rsinθsinϕx′=rcosθcosϕ−rsinθsinϕ
y′=rsinθcosϕ+rcosθsinϕy′=rsinθcosϕ+rcosθsinϕ
带入x和y表达式得到
x′=xcosθ−ysinθx′=xcosθ−ysinθ
y′=xsinθ+ycosθy′=xsinθ+ycosθ
写成矩阵的形式是：
[x′y′]=[cosθsinθ−sinθcosθ]∗[xy][x′y′]=[cosθ−sinθsinθcosθ]∗[xy]
尽管图示中仅仅表示的是旋转一个锐角θθ的情形，但是我们推导中使用的是三角函数的基本定义来计算坐标的，因此当旋转的角度是任意角度（例如大于180度，导致v’点进入到第四象限）结论仍然是成立的。
绕原点的旋转是二维旋转最基本的情况，当我们需要进行绕任意点旋转时，我们可以把这种情况转换到绕原点的旋转，思路如下：
1. 首先将旋转点移动到原点处
2. 执行如2所描述的绕原点的旋转
3. 再将旋转点移回到原来的位置
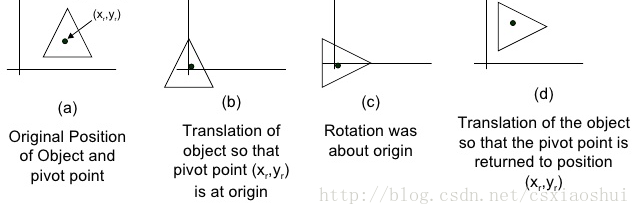
也就是说在处理绕任意点旋转的情况下需要执行两次平移的操作。假设平移的矩阵是T(x,y)，也就是说我们需要得到的坐标 v’=T(x,y)*R*T(-x,-y)（我们使用的是列坐标描述点的坐标，因此是左乘，首先执行T(-x,-y)）
在计算机图形学中，为了统一将平移、旋转、缩放等用矩阵表示，需要引入齐次坐标。（假设使用2x2的矩阵，是没有办法描述平移操作的，只有引入3x3矩阵形式，才能统一描述二维中的平移、旋转、缩放操作。同理必须使用4x4的矩阵才能统一描述三维的变换）。
对于二维平移，如下图所示，P点经过x和y方向的平移到P’点，可以得到：
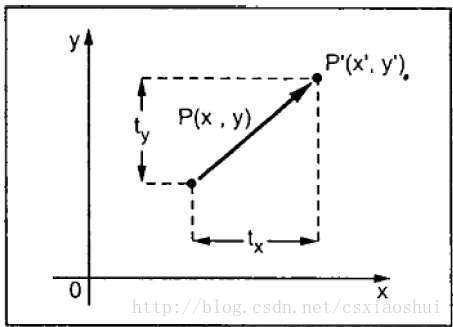
x′=x+txy′=y+tyx′=x+txy′=y+ty
由于引入了齐次坐标，在描述二维坐标的时候，使用（x，y，w）的方式（一般w=1），于是可以写成下面矩阵的形式
⎡⎣⎢x′y′1⎤⎦⎥=⎡⎣⎢100010txty1⎤⎦⎥∗⎡⎣⎢xy1⎤⎦⎥[x′y′1]=[10tx01ty001]∗[xy1]
按矩阵乘法展开，正好得到上面的表达式。也就是说平移矩阵是
⎡⎣⎢100010txty1⎤⎦⎥[10tx01ty001]
如果平移值是（-tx，-ty）那么很明显平移矩阵式
⎡⎣⎢100010−tx−ty1⎤⎦⎥[10−tx01−ty001]
我们可以把2中描述的旋转矩阵也扩展到3x3的方式，变为：
⎡⎣⎢x′y′1⎤⎦⎥=⎡⎣⎢cosθsinθ0−sinθcosθ0001⎤⎦⎥∗⎡⎣⎢xy1⎤⎦⎥[x′y′1]=[cosθ−sinθ0sinθcosθ0001]∗[xy1]
从平移和旋转的矩阵可以看出，3x3矩阵的前2x2部分是和旋转相关的，第三列与平移相关。有了上面的基础之后，我们很容易得出二维中绕任意点旋转的旋转矩阵了，只需要把三个矩阵乘起来即可：
M=⎡⎣⎢100010txty1⎤⎦⎥∗⎡⎣⎢cosθsinθ0−sinθcosθ0001⎤⎦⎥∗⎡⎣⎢100010−tx−ty1⎤⎦⎥=⎡⎣⎢cosθsinθ0−sinθcosθ0(1−cosθ)tx+ty∗sinθ(1−cosθ)ty−tx∗sinθ1⎤⎦⎥M=[10tx01ty001]∗[cosθ−sinθ0sinθcosθ0001]∗[10−tx01−ty001]=[cosθ−sinθ(1−cosθ)tx+ty∗sinθsinθcosθ(1−cosθ)ty−tx∗sinθ001]
我们可以把一个旋转转换为绕基本坐标轴的旋转，因此有必要讨论一下绕三个坐标值x、y、z的旋转。
本文在讨论过程中使用的是类似于OpenGL中定义的右手坐标系，同时旋转角度的正负也遵循右手坐标系的约定。如下图所示
4.1 绕X轴的旋转
在三维场景中，当一个点P(x,y,z)绕x轴旋转θθ角得到点P’(x’,y’,z’)。由于是绕x轴进行的旋转，因此x坐标保持不变，y和z组成的yoz（o是坐标原点）平面上进行的是一个二维的旋转，可以参考上图（y轴类似于二维旋转中的x轴，z轴类似于二维旋转中的y轴），于是有：
x′=xx′=x
y′=ycosθ−zsinθy′=ycosθ−zsinθ
z′=ysinθ+zcosθz′=ysinθ+zcosθ
写成（4x4）矩阵的形式
⎡⎣⎢⎢⎢x′y′z′1⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢10000cosθsinθ00−sinθcosθ00001⎤⎦⎥⎥⎥∗⎡⎣⎢⎢⎢xyz1⎤⎦⎥⎥⎥[x′y′z′1]=[10000cosθ−sinθ00sinθcosθ00001]∗[xyz1]
4.2 绕Y轴旋转
绕Y轴的旋转和绕X轴的旋转类似，Y坐标保持不变，除Y轴之外，ZOX组成的平面进行一次二维的旋转（Z轴类似于二维旋转的X轴，X轴类似于二维旋转中的Y轴，注意这里是ZOX，而不是XOZ，观察上图中右手系的图片可以很容易了解到这一点），同样有：
x′=zsinθ+xcosθx′=zsinθ+xcosθ
y′=yy′=y
z′=zcosθ−xsinθz′=zcosθ−xsinθ
写成（4x4）矩阵的形式
⎡⎣⎢⎢⎢x′y′z′1⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢cosθ0−sinθ00100sinθ0cosθ00001⎤⎦⎥⎥⎥∗⎡⎣⎢⎢⎢xyz1⎤⎦⎥⎥⎥[x′y′z′1]=[cosθ0sinθ00100−sinθ0cosθ00001]∗[xyz1]
4.3 绕Z轴旋转
与上面类似，绕Z轴旋转，Z坐标保持不变，xoy组成的平面内正好进行一次二维旋转（和上面讨论二维旋转的情况完全一样）
⎡⎣⎢⎢⎢x′y′z′1⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢cosθsinθ00−sinθcosθ0000100001⎤⎦⎥⎥⎥∗⎡⎣⎢⎢⎢xyz1⎤⎦⎥⎥⎥[x′y′z′1]=[cosθ−sinθ00sinθcosθ0000100001]∗[xyz1]
4.4 小结
上面描述了三维变换中绕单一轴旋转的矩阵表达形式，绕三个轴旋转的矩阵很类似，其中绕y轴旋转的矩阵与绕x和z轴旋转的矩阵略有点不同（主要是三个轴向顺序和书写矩阵的方式不一致导致的，绕三个不同坐标旋转轴以及其他二个坐标轴组成平面的顺序是： XYZ(绕x轴） YZX（绕y轴） ZXY（绕z轴），其中绕y轴旋转，其他两个轴是ZX，这和我们书写矩阵按
⎡⎣⎢⎢⎢xyz1⎤⎦⎥⎥⎥[xyz1]
的方式不一致，而导致看起来绕Y轴旋转的矩阵似乎是和其他两个矩阵不一致。如果我们颠倒写法，将公式写成
⎡⎣⎢⎢⎢z′y′x′1⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢cosθ0sinθ00100−sinθ0cosθ00001⎤⎦⎥⎥⎥∗⎡⎣⎢⎢⎢zyx1⎤⎦⎥⎥⎥[z′y′x′1]=[cosθ0−sinθ00100sinθ0cosθ00001]∗[zyx1]
的方式，那么这三个旋转矩阵看起来在形式上就统一了，都是
[cosθsinθ−sinθcosθ][cosθ−sinθsinθcosθ]
这种表现形式了（左上角都是−sinθ−sinθ）
绕任意轴的三维旋转可以使用类似于绕任意点的二维旋转一样，将旋转分解为一些列基本的旋转。绕任意轴旋转如下图所示：
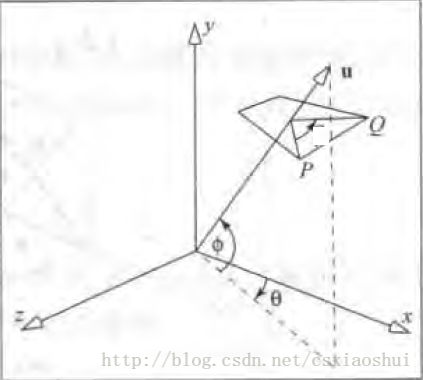
P点绕向量u旋转θθ角，得到点Q，已知P点的坐标和向量u，如何求Q点的坐标。
我们可以把向量u进行一些旋转，让它与z轴重合，之后旋转P到Q就作了一次绕Z轴的三维基本旋转，之后我们再执行反向的旋转，将向量u变回到它原来的方向，也就是说需要进行的操作如下：
1. 将旋转轴u绕x轴旋转至xoz平面
2. 将旋转轴u绕y轴旋转至于z轴重合
3. 绕z轴旋转θθ角
4. 执行步骤2的逆过程
5. 执行步骤1的逆过程
原始的旋转轴u如下图所示：
第1、2、3步骤如下图所示：
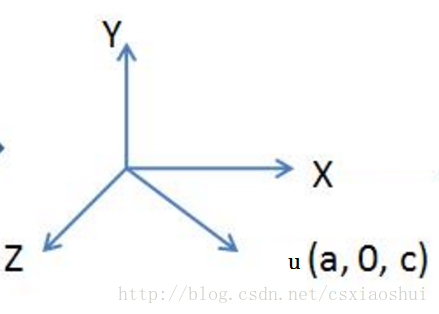
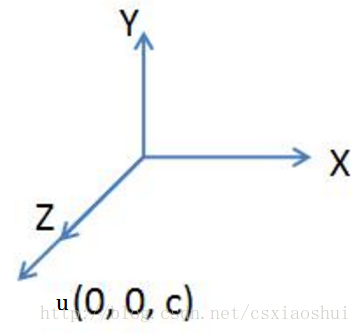
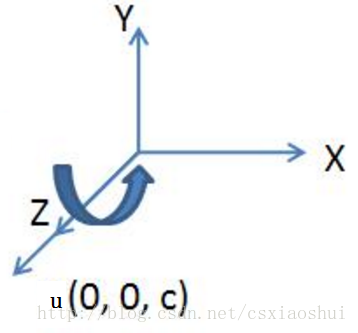
步骤1将向量u旋转至xoz平面的操作是一个绕x轴的旋转操作，步骤2将向量u旋转到与z轴重合，第1、2步骤的示意图如下：
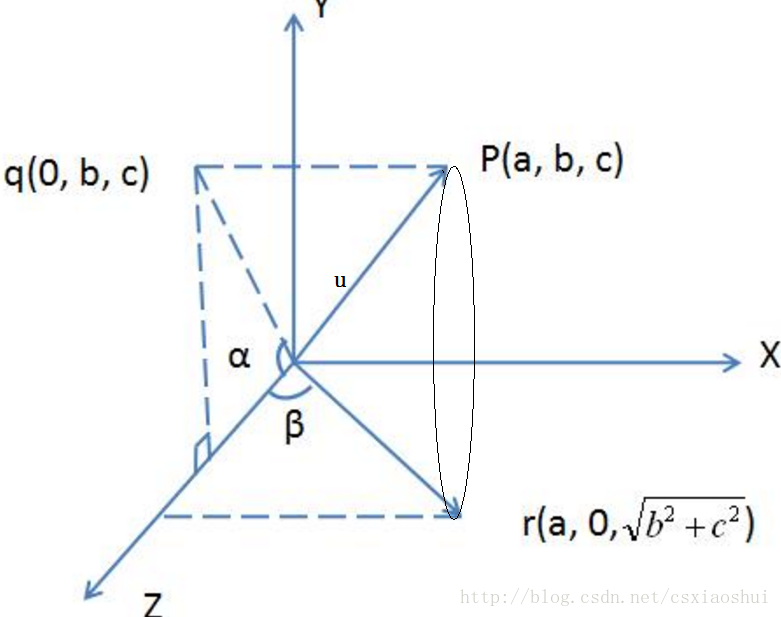
作点P在yoz平面的投影点q，q的坐标是（0, b, c)，原点o与q点的连线oq和z轴的夹角就是u绕x轴旋转的角度。通过这次旋转使得u向量旋转到xoz平面（图中的or向量）【步骤1】
过r点作z轴的垂线，or与z轴的夹角为ββ, 这个角度就是绕Y轴旋转的角度，通过这次旋转使得u向量旋转到与z轴重合【步骤2】
步骤1中绕x轴旋转的是一次基本的绕x轴的三维旋转，按照之前的讨论，旋转矩阵是：
⎡⎣⎢⎢⎢10000cosθsinθ00−sinθcosθ00001⎤⎦⎥⎥⎥[10000cosθ−sinθ00sinθcosθ00001]
这里的θθ就是图中所示的αα角 （注意αα角度是绕x旋转的正的角度）
从图中我们还可以得到：
cosα=c(b2+c2)−−−−−−−√cosα=c(b2+c2)
sinα=b(b2+c2)−−−−−−−√sinα=b(b2+c2)
于是旋转矩阵(记作 Rx(α)Rx(α))为：
⎡⎣⎢⎢⎢⎢⎢⎢⎢10000c(b2+c2)√b(b2+c2)√00−b(b2+c2)√c(b2+c2)√00001⎤⎦⎥⎥⎥⎥⎥⎥⎥[10000c(b2+c2)−b(b2+c2)00b(b2+c2)c(b2+c2)00001]
在完成步骤1之后，向量u被变换到了r的位置，我们继续步骤2的操作，绕y轴旋转负的ββ角（注意：这里的ββ是负的），经过这次变换之后向量u与z轴完全重合，由于这一步也是执行的一次绕Y轴的基本旋转，旋转矩阵（记作 Ry(−β)Ry(−β))为：
⎡⎣⎢⎢⎢cosθ0−sinθ00100sinθ0cosθ00001⎤⎦⎥⎥⎥[cosθ0sinθ00100−sinθ0cosθ00001]
使用−β−β替换表达式中的θθ，此外根据图中描述，我们可以计算得到：
cosβ=(b2+c2)−−−−−−−√(a2+b2+c2)−−−−−−−−−−−√cosβ=(b2+c2)(a2+b2+c2)
sinβ=a(a2+b2+c2)−−−−−−−−−−−√sinβ=a(a2+b2+c2)
带入上面的表达式，于是旋转矩阵(记作 Ry(−β)Ry(−β))为：
⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢(b2+c2)√(a2+b2+c2)√0a(a2+b2+c2)√00100−a(a2+b2+c2)√0(b2+c2)√(a2+b2+c2)√00001⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥[(b2+c2)(a2+b2+c2)0−a(a2+b2+c2)00100a(a2+b2+c2)0(b2+c2)(a2+b2+c2)00001]
在完成前面两个步骤之后，u方向和z轴完全重合，因此执行旋转θθ角，执行的是一次绕z轴的基本三维旋转（记作 R(θ)R(θ)，根据之前的讨论，我们可以得到：
⎡⎣⎢⎢⎢cosθsinθ00−sinθcosθ0000100001⎤⎦⎥⎥⎥[cosθ−sinθ00sinθcosθ0000100001]
最后两步骤是前面1和2的逆操作，也就是绕Y轴旋转ββ 和绕X轴旋转−α−α，这两个矩阵分别记作 Ry(β)Ry(β) 和 Rx(−α)Rx(−α)，得到它们的方式很简单，只需要将上面步骤1和步骤2中的角度修改成相反数即可，也就是：
Ry(β)=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢(b2+c2)√(a2+b2+c2)√0−a(a2+b2+c2)√00100a(a2+b2+c2)√0(b2+c2)√(a2+b2+c2)√00001⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥Ry(β)=[(b2+c2)(a2+b2+c2)0a(a2+b2+c2)00100−a(a2+b2+c2)0(b2+c2)(a2+b2+c2)00001]
Rx(−α)=⎡⎣⎢⎢⎢⎢⎢⎢⎢10000c(b2+c2)√−b(b2+c2)√00b(b2+c2)√c(b2+c2)√00001⎤⎦⎥⎥⎥⎥⎥⎥⎥Rx(−α)=[10000c(b2+c2)b(b2+c2)00−b(b2+c2)c(b2+c2)00001]
最终得到 绕任意轴u旋转的旋转矩阵是【因为使用的列向量，因此执行的是左乘（从右往左）】：
MR=Rx(−α)Ry(β)Rz(θ)Ry(−β)Rx(α)=MR=Rx(−α)Ry(β)Rz(θ)Ry(−β)Rx(α)=
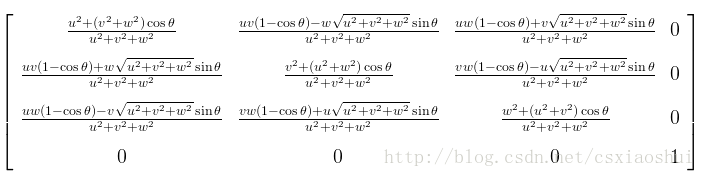
(注：式中的(u,v,w)对应上文中向量(a,b,c)，公式我自己笔算过，为了减少编辑公式的时间（使用LaTex编辑太繁琐，因此找了一张公式的图片贴在此处)
如果向量是经过单位化的（单位向量），那么有a2+b2+c2=1a2+b2+c2=1，可以简化上述的公式，得到：
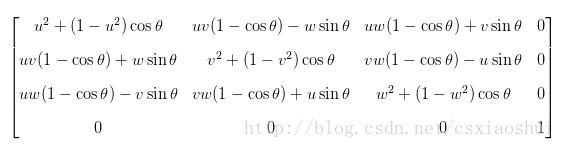
--------------------- 本文来自 csxiaoshui 的CSDN 博客 ，全文地址请点击：https://blog.csdn.net/csxiaoshui/article/details/65446125?utm_source=copy
