区间动归
“某类有序事件中前若干个事件的子答案”不能再支撑状态转移,我们需要去寻找“从某个元素起到另一个元素结束所包含所有的(连续)元素的子答案”作为状态。
可以想象,在这个描述下,每个状态会对应于原题序列上的一个区间。区间具有良好的性质:短的区间可以拓宽成长的区间,相同长度的区间互相不包含。这样,可以把所有状态理解成DAG,即不会有可以互相到达的局面。
像这样以区间左右端点来描述状态,一个状态由比它更小的其他状态转移而来的动归,称为“区间动归”。转移时要考虑边界上的变化。边界条件一般是最小单位的区间(即i=j的情况下)。
例题1:石子合并弱化版
有 n 堆石子堆放在路边,现要将石子有序地合并成一堆,规定每次只能移动相邻的两堆石子合并,合并花费为新合成的一堆石子的数量。求将这 N 堆石子合并成一堆的总花费(最小或最大)。
样例输入
5
1 2 3 4 5
样例输出
33
【问题解析】
首先,列出石子 进行观察。A[i]为该堆中的石子个数
1.□ 2.□□ 3.□□□ 4.□□□□ 5.□□□□□
1.若石子有1堆,则无需合并,花费为0
2.若石子有2堆,则合并二者,花费为A[0]+A[1]
3.若石子有3堆,则有2种情况,①先合并A[0]、A[1]再与A[2]合并 ②先合并A[1]、A[2]再与A[0]合并
4.若石子有4堆,则有3种情况,...............
总之,在n堆中,有n-1种情况,而最后一次合并总是以某两堆合成一堆为结果。
即可将n堆划分成A[0...k] 与 A[k+1...n-1]合并,
而A[0...k] 与 A[k+1...n-1]已是最优花费,由各自向下分解所得。假设有5堆石子,则A[0...k] 与 A[k+1...n-1]的长度堆数可能为 1、4 。 2、3 。 3、2 。 4、1
只要其各自已为最优花费。
以上为递推向下的逻辑,在动态规划是由下而上,即5堆石子 需要长度为 2 3 4 的石子最优花费
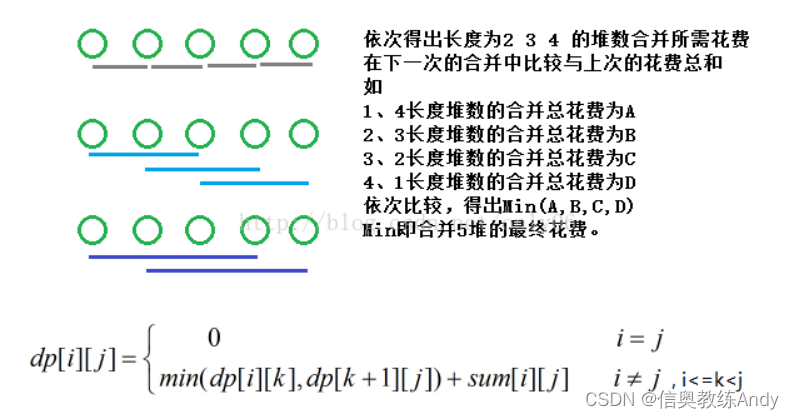
然后开始分析算法过程,首先,最外层循环 控制石子堆长度(len=2 to n),因为只有1堆时无需下续步骤
接着第二层循环,确定石子堆的起始堆号(i=0 to n-len)即为图中的下划线个数。
继续分析,发现还需要一层循环控制更新 A[0…k] 与 A[k+1…n-1]的花费price (k=i to j-1)
确定无遗漏后,开始编写代码过程,如下。
(注意,花费是每两两合并完的石子数依次相加,所以最后一次合并为合并堆数的总石子量)
由sum[i][j]表示第i堆石子到第j堆石子全部合并的总石子量。dp[i][j]为第i堆石子到第j堆合并的花费(随着动态规划的进行,会越来越越接近最优花费)dp[i][i]=0 (本身无需合并,不需花费)
即若仅两堆石子合并 则dp[i][j]=dp[i][i]+dp[j][j]+sum[i][j] = 0+0+sum[i][j]
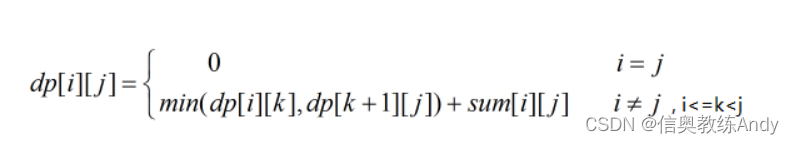
归纳总结
( 1 )建立最优值递归式
设 Min [i][j] 代表从第 i 堆石子到第 j 堆石子合并的最小花费, Min [i][k] 代表从第 i 堆石子到第 k 堆石子合并的最小花费,Min[k+1][j] 代表从第 k+1 堆石子到第 j 堆石子合并的最小花费, w ( i , j )代表从 i 堆到 j 堆的石子数量之和。列出递归式:
Min [ i ][ j ] = 0 (i = j)
Min [ i ][ j ] = min ( Min [ i ][ k ] + Min [ k + 1][ j ] + w ( i , j )) , i < j( i ≤ k < j)
Max [i][j] 代表从第 i 堆石子到第 j 堆石子合并的最大花费,Max [i][k] 代表从第 i 堆
石子到第 k 堆石子合并的最大花费,Max [k+1][j] 代表从第 k+1 堆石子到第 j 堆石子合并的最大花费, w ( i , j )代表从 i 堆到 j 堆的石子数量之和。列出递归式:
Max [ i ][ j ] = 0 (i = j)
Max [ i ][ j ] =max( Max [ i ][ k ] + Max [ k + 1][ j ] + w ( i , j )) , i < j ( i ≤ k < j)
二维数组 Min [i][j] 、Max [i][j] 来记录第 i 堆到第 j 堆 a i , a i+1 ,…, a i 堆石子合并的最小花费和最大花费。
( 2 )初始化
输入石子的堆数 n ,然后依次输入各堆石子的数量存储在 a[i] 中,令 Min [i][i]=0 ,
Max [i][i]=0 , sum[0]=0 ,计算 sum[i] ,其中 i= 1 , 2 , 3 ,…, n 。
( 3 )循环阶段
• 按照递归式计算 2 堆石子合并 {a i , a i+1 } 的最小花费和最大花费, i=1 , 2 , 3 ,…, n−1 。
• 按照递归式计算 3 堆石子合并 {a i , a i+1 , a i+2 } 的最小花费和最大花费, i=1 , 2 , 3 ,…,n−2 。
•
#define M 101
#define INF 1000000000
int n,f[M][M],sum[M][M],stone[M];
int main()
{
int i,j,k,t;
cin>>n;
for(i=1;i<=n;i++)
scanf("%d",&stone[i]);
for(i=1;i<=n;i++)
{
f[i][i]=0;
sum[i][i]=stone[i];
for(j=i+1;j<=n;j++)
sum[i][j]=sum[i][j-1]+stone[j];
}
for(int len=2;len<=n;len++)//归并的石子长度
{
for(i=1;i<=n-len+1;i++)//i为起点,j为终点
{
j=i+len-1;
f[i][j]=INF;
for(k=i;k<=j-1;k++)
{
f[i][j]=min(f[i][k]+f[k+1][j])+sum[i][j];
}
}
}
printf("%d/n",f[1][n]);
return 0;
}
环形动归
例题:石子合并
在加上环形的限制条件下,其实只需要将环在某一点切断,变成线性来处理。
可以证明一定存在一个“断点”在某两个相邻的石子中间,对于任意环上的合并方式,都不会跨越这个断点进行合并。因此,可以将这个环破成一个链来处理。
如果每次从环中生成一个新的链,分别进行DP,则时间复杂度无法接受。所以可以将这个序列复制一次,变成长度为2N的序列。其中每一个长度为N的连续子序列都是剪开的一条链。剩下的事情和上面一样啦。
代码实现时,长度还是从1枚举到N,但原始链的长度扩大一倍。
#include<bits/stdc++.h>
using namespace std;
#define maxn 205
#define inf 0x7f7f7f7f
int a[maxn],sum[maxn]={0};
int f1[maxn][maxn],f2[maxn][maxn];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
a[i+n]=a[i];
}
for(int i=1;i<=n*2;i++)
sum[i]=sum[i-1]+a[i];
memset(f1,0,sizeof(f1));
//memset(f2,inf,sizeof(f2));
for(int L=2;L<=n;L++)
for(int i=1;i+L-1<=n*2;i++)
{
int j=i+L-1;
f2[i][j]=inf;
for(int k=i;k<j;k++)
{
f1[i][j]=max(f1[i][j],f1[i][k]+f1[k+1][j]+sum[j]-sum[i-1]);
f2[i][j]=min(f2[i][j],f2[i][k]+f2[k+1][j]+sum[j]-sum[i-1]);
}
}
int ans1=-inf;
int ans=inf;
for(int i=1;i<=n;i++) ans1=max(ans1,f1[i][i+n-1]);
for(int i=1;i<=n;i++) ans=min(ans,f2[i][i+n-1]);
cout<<ans<<endl<<ans1;
}
课后练习
1、回文字串
2、道路游戏
3、能量项链