万里之行，始于足下。本博客总结近期学习到的部分数论模板，以便于日后查询使用。作者水平有限，难免存在疏漏不足，恳请诸位看官斧正。倘若我的文章可以帮到你，十分荣幸。当然，以后随着我的阅历知识增长还敬请期待后序更新。本次内容的灵感来自于lyh学长和lyk学长的讲课和近期的牛客竞赛补题。
目录
1.素数筛
（1）何谓素数？
（2）朴素筛法
（3）埃氏筛（sieve of Eratosthenes）
（4）欧拉筛（sieve of euler）
2.费马小定理(Fermat's little theorem)
（1）何谓费马小定理？
（2）费马小定理求逆元
（3）线性逆元的讨论
3.lcm与gcd
（1）最大公因数（gcd）
（2）最小公倍数（lcm）
4.欧拉降幂
更新日志：
1.于2022.4.16修正了朴素筛法的代码部分。
总结方法前我们不妨先回溯一下知识点：什么是素数？素数又名质数，百度百科对它的定义是：质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。
注意：0和1不是素数！
这里有素数的两个定理，在后面的解题中比较重要：
唯一分解定理：任何一个大于1的自然数n，那么n可以唯一分解成有限个不相同的质数的乘积n = p1^a1 * p2^a2 * ... * pn^an（an为正整数）。
素数分布规律：素数的分布是越往后越稀疏的，一般来说区间内的素数个数是小于等于区间长度的1/3的。
一个数是不是素数是好判断的。但是计算机的问题规模往往会成千上万。怎么高效地找出一个范围内的素数？接下来会介绍三种筛法，如沙中淘金，找出一个范围内的素数。
高情商：朴素 低情商：暴力
一个一个枚举区间里的数，利用素数的定义判断枚举到的数是不是素数。
bool isprime(int x){
if(x<2) return false;//0和1不是素数也不是合数哦！
for(int i=2;i*i<=x;i++){
if(x%i==0) return false;
}
return true;
}嗯哼？为什么是i * i <= x而不是i <= x？因为一个数的最大因子是不会超过它的二次根号的。这是一个小小的细节优化。
bool numlist[maxn];//标记这个数是不是素数；maxn根据要求的范围确定
vector<int> prime;//vector容器存放求到的素数
void Eratosthenes(int n)
{
memset(numlist,true,sizeof (numlist));
numlist[0]=numlist[1]= false;//0和1不是素数哦
for(int i=2;i<=n;i++)
{
if(numlist[i])
{
prime.push_back(i);//放入vector容器
for(int j=i;i*j<=n;j++)
{
numlist[i*j]= false;//素数的倍数不是素数
}
}
}
}不难发现，埃氏筛法在枚举k的每一个质因子时，都计算了一次k，造成了重复筛除。那么还可不可以再优化一下呢？
bool numlist[maxn];//标记这个数是不是素数；maxn根据要求的范围确定
vector<int> prime;//vector容器存放求到的素数
void euler()
{
memset(numlist,true,sizeof(numlist));
numlist[0]=numlist[1]=false;//注意0和1不是素数哦
for(int i=2;i<=n;i++)
{
if(numlist[i]) prime.push_back(i);//将求得的素数放入容器
for(int j=0;j<prime.size()&&i*prime[j]<=n;j++)
{
numlist[i*prime[j]]=false;//素数的倍数不是素数
if(i%prime[j]==0) break;//退出循环
}
}
}问题来了：为什么终止条件是i%prime[j]==0？若i%prime[j]==0，则有i =x * prime[j]，则对于prime[j+1]有i * prime[j+1] = prime[j] * x * prime[j+1]；因为我们是从小到大枚举素数的，那么又可以说i已经被prime[j]筛过了，所以i乘其他质数的结果也一定是prime[j]的倍数，那么会通过prime[j]筛出，因此不需再筛直接退出。
通过例题理解一下：洛谷-P3383 【模板】线性筛素数
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,q;
const ll maxn=1e8+7;
bool numlist[maxn];//标记这个数是不是素数；maxn根据要求的范围确定
vector<int> prime;//vector容器存放求到的素数
void euler()
{
memset(numlist,true,sizeof(numlist));
numlist[0]=numlist[1]=false;//注意0和1不是素数哦
for(int i=2;i<=n;i++)
{
if(numlist[i]) prime.push_back(i);//将求得的素数放入容器
for(int j=0;j<prime.size()&&i*prime[j]<=n;j++)
{
numlist[i*prime[j]]=false;//素数的倍数不是素数
if(i%prime[j]==0) break;//退出循环
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>q;
euler();
for(int i=1;i<=q;i++)
{
ll t;
cin>>t;
cout<<prime[t-1]<<endl;
}
return 0;
}这一题对时间复杂度的要求比较苛刻，所以我采用了欧拉筛（埃氏筛貌似也可）来预处理范围内的所有数，筛出素数存于容器中待用。
费马小定理(Fermat's little theorem)是数论中的一个重要定理，在1636年提出。如果p是一个素数，而整数a不是p的倍数，则有a^（p-1）≡1（mod p）。
逆元素是指一个可以取消另一给定元素运算的元素。比如说乘法运算中，一个数的逆元是它的倒数。逆元定义为ax ≡ 1 (mod p)，再根据费马小定理得 ax ≡ a^(p−1) (mod p)。所以x的逆元为 x ≡ a^(p−2) (mod p)。这样我们直接使用快速幂就可以求出逆元。在mod p条件下，使用逆元做除可以避免取模带来除数的改变。特别注意此方法只适合p为质数的情况下使用。
例题：牛客竞赛-智乃酱的区间乘积
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
ll a[100007],s[100007];
ll n,m;
typedef long long ll;
ll qpow(ll x,ll n)//快速幂
{
ll ans=1;
x%=mod;
while(n)
{
if(n&1)
{
ans=ans*x%mod;
}
x=x*x%mod;
n>>=1;
}
return ans;
}
ll get_inv(ll x)//求x的逆元
{
return qpow(x,mod-2);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
s[0]=1;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=n;i++)
{
s[i]=s[i-1]*a[i]%mod;//类似于前缀和
}
for(int i=1;i<=m;i++)
{
ll l,r;
cin>>l>>r;
cout<<s[r]*get_inv(s[l-1])%mod<<endl;//相当于s[r]/s[l-1]
}
return 0;
}这一题求区间乘积类似于查询区间和，所以我们用到了“前缀和”（下次有机会也讲一讲qwq），当然这里的s[i]其实是前i个元素的乘积。因为前i个数相乘可能会很大很大，所以我们在计算s[i]的时候取了模。问题来了：最后询问的时候需要做除法怎么办？
利用费马小定理，我们知道在mod p的条件下是和
等价的。所以尽管我们不能直接除s[l]，但是可以用乘s[l]的逆元来代替除s[l]没有取模的原始值，也就是前l个数的乘积。
ll inv[maxn];//存储逆元
void solve(int n,ll p)
{
inv[1]=1;
for(int i=2;i<=n;i++)
{
inv[i]=(p-p/i)*inv[p%i]%p;
}
} 这个定义相信聪明的你一定会
可以用c++自带的库函数 __gcd(a,b)，其中a，b不能为浮点数。亦或使用欧几里得算法，时间复杂度为O(log n)。
typedef long long ll;
ll gcd(ll a,ll b)
{
return b==0?a:gcd(b,a%b);
}gcd的一些性质：
gcd(a, b) = c -> gcd(a / c,b / c) = 1
gcd(a * b, c), a ⊥ c -> gcd(b, c) （注意在代数中，“⊥”指互质）
gcd(a, b, c) = gcd( gcd(a, b), c)。 gcd的区间可加性，可以应用于线段树或dp等。
typedef long long ll;
ll lcm(ll a,ll b)
{
return a/gcd(a,b)*b;
}注意这里的a先除gcd再乘b，可以防止可能的a * b过大导致溢出。
例题：牛客竞赛-区间合数的最小公倍数
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
int l,r;
ll ans=1;
vector<int> isprime;
bool judge(int x)
{
for(int i=2;i*i<=x;i++)
{
if(x%i==0) return false;
}
return true;
}
void prime()//朴素筛法
{
for(int i=2;i<=30000;i++)
{
if(judge(i)) isprime.push_back(i);
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
prime();
cin>>l>>r;
for(int i=0; isprime[i]*2<=r;i++)
{
int j;
for(j=isprime[i];j<=r;j*=isprime[i])
{
if(r/j==(l-1)/j) break;
}
ans*=j/isprime[i];//求区间质数的最高次幂
ans%=mod;
}
if(ans==1)
{
cout<<"-1"<<endl;
}
else
{
cout<<ans<<endl;
}
}
这里就运用到了一个lcm的性质：求区间所有合数的最小公倍数，需要统计区间内每个素数出现的最高的幂。例如，a=，b=
，c=
，则它们的lcm为
，也就是每个素数的幂取最大值的乘积。
当然，这里还用到了上面讲到的素数筛法。
怎么又是欧拉先引入问题：牛客竞赛-子序列权值乘积
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
ll n,a[200007],ans=1;
ll qpow(ll x,ll n,ll p=mod)//快速幂
{
ll ans=1;
x%=p;
while(n)
{
if(n&1)
{
ans=ans*x%p;
}
x=x*x%p;
n>>=1;
}
return ans;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
sort(a,a+n);//升序排序
for(int i=0;i<n;i++)
{
ll sum=qpow(2,i,mod-1)+ qpow(2,n-i-1,mod-1);//欧拉降幂
ans*=qpow(a[i],sum);//计算，每个数对最终答案的贡献
ans%=mod;
}
cout<<ans<<endl;
}我们选择先对序列进行升序排序，而后计算每个数k做序列最小值的次数，也就是2^(k后面的数的个数)，同理计算出k做序列最大值的次数，这里是需要用到快速幂的。这个数很大，对吧？然后我们还要累计这个数作为k的幂的乘积，也就是k对答案的贡献。
在这种幂比较大的情况，例如 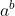,令b=k(p-1)+c，则有
。其中由上文中的费马小定理有
，则可化简为
(mod p)。而 c=b%(p-1)，也就是说，我们可以通过对幂模p-1来实现降幂化简。
“艰难方显勇毅，磨砺始得玉成。”大二下学期的课程和实验更多，更难，蓝桥杯，天梯赛，icpc昆明站也要来了。人的一生求上，未必居中；求中，可能居下；求下，必不入流。青春年少，风华正茂，立志必高远，学得雄鹰展翅飞，莫效燕雀安于栖，共勉！