Kuhn-Munkres 算法详细解析

直接进入正题，Kuhn-Munkres 算法（下文简称 KM 算法）是为了高效求解二分图最佳完美匹配问题而生的，我们先温习一下几个概念，如果你对这几个概念不是很熟悉的话，建议先去学习。

概念

• 匹配（匹配边）： 在图 GG 中两两没有公共端点的边集合 MM。
• 二分图最大匹配：给出一个二分图，找一个边数最大的匹配。即选尽可能多的边，使得任意选中的两条边均没有公共顶点。

不要被概念弄的晕了，用最直观的方式考虑。情景是有一个班级的学生要结成男女两两一组，但每个学生只想自己喜欢的异性结成一组，于是这就会有冲突。由于男男、女女不会结成一组，这是一个二分图。二分图最大匹配就是要给出一个最优方案，使得结成的组数最多。

下面说复习二分图最大匹配相关：
为了方便叙述，我们将二分图染色后同颜色的节点放在同一侧，形成左侧（XX 集），右侧（YY 集）。

• 交替路：从任意一个未匹配点出发，依次经过未匹配边－匹配边－非匹配边－匹配边－未匹配边……所得到的路径被称为交替路。
• 增广路：如果一条交替路的终点是一个未匹配点，那么这条路径是增广路，由于从未匹配点出发，又从未匹配点结束，未匹配边比未配边多一条。
• 增广路定理：如果可以找到一条增广路，那么将匹配边与未匹配边互换，这个匹配就可以多一条边，否则当前匹配就是最大匹配。即任意一个匹配是最大匹配的充分必要条件是不存在增广路。

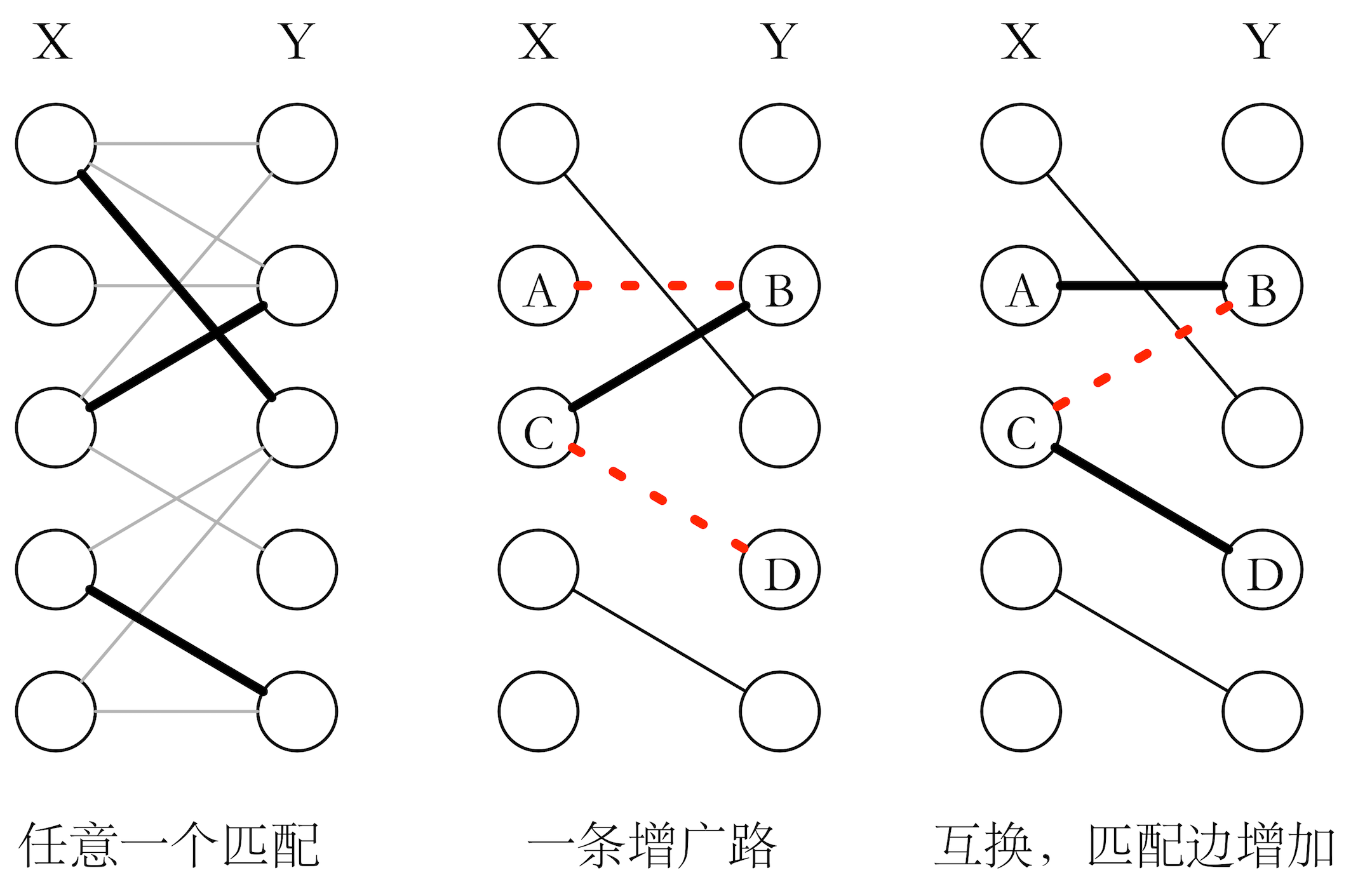
增广路互换的实质可以这么考虑，如上图：从未匹配点 A 出发，A 想与 B 匹配，于是通过未匹配边找到 B，然而 B 已经是匹配点，于是只能经过匹配边去问 C 能不能与别人匹配，C 经过未匹配边找到 D，由于 D 是未匹配点，所以 C 成功与 D 匹配。CD 之间的边变为匹配边；BC 之间解除关系，变为未匹配边；AB 之间建立关系，变为匹配边。这便是增广路互换的实质。

• 二分图完美匹配：如果一个二分图的所有点都是匹配点（匹配边中某一条边的端点），则称这个匹配是完美匹配。

回到上面的情景，完美匹配就是可以得到一个方案，使得所有男女同学都可以结成两两一组。

• 二分图最大完美匹配：假定有一个二分图 GG，每条边有一个权值（可为负数），权值和最大的完美匹配是二分图最大完美匹配。

算法

KM 算法是通过给每个顶点一个标号（叫做顶标）来把求最大权完美匹配的问题转化为求完美匹配的问题的。可以简单理解为节点函数就是节点的一个值。
可行顶标就是对于所有顶点的函数值 ll，使得对于任意弧 e(x \rightarrow y)e(x→y)，都满足 l_{x} + l_{y} \ge W_{e}l​x​​+l​y​​≥W​e​​, KM 算法的顶标自始至终满足这一条件。
接着是相等子图，相等子图包含原图中所有的点，但只包含满足 l_{x} + l_{y} = W_{e}l​x​​+l​y​​=W​e​​ 的所有弧 e(x \rightarrow y)e(x→y)，根据定义，这些弧一定是当前最大的弧（不等式已经取到等号），那么如果相等子图有完美匹配，那这个完美匹配一定是最大完美匹配。因为相等子图的权值和为所有点的顶标之和，而随便一个匹配中的边因为受到 W_{e} \le l_{x} + l_{y}W​e​​≤l​x​​+l​y​​ 的限制，不可能比所有点的顶标之和大，所以这个极为重要的定理还是很好证明的。
所以算法的主要矛盾就在于寻找可行顶标，使得相等子图有完美匹配。可行顶标的修改过程中，每一步都运用了贪心的思想，这样我们的最终结果一定是最优的。下面是算法的叙述：
因为有 l_{x} + l_{y} = W_{e}l​x​​+l​y​​=W​e​​ 恒成立，我们设左侧（YY 集）的所有节点顶标为 00，那么所有 XX 集的点的顶标就必须为从它出发所有的边的最大值。
接着求其完美匹配，如果成功，结束算法，否则必须修改顶标，使得有更多的边能够参与进来。
我们求当前相等子图的完美匹配失败，是因为对于某个未匹配顶点 uu，我们找不到一条从它出发的增广路，这时我们只能获得一条交替路。我们把 XX 集中在交替路的点集叫做 SS， XX 集中不在交替路的点集叫做 S'S​′​​，同理 YY 集中在交替路的点集叫做 TT， YY 集中不在交替路的点集叫做 T'T​′​​。
如果我们把交替路中 XX 集顶点的顶标全都减小某个值 dd，YY 集的顶标全都增加同一个值 dd，那么我们会发现：

• 两端都在交替路中的边 e(i \rightarrow j)e(i→j)，l_{i} + l_{j}l​i​​+l​j​​ 的值没有变化。也就是说，它原来属于相等子图，现在仍属于相等子图。
• 两端都不在交替路中的边 e(i \rightarrow j)e(i→j)，l_{i}, l_{j}l​i​​,l​j​​ 都没有变化。也就是说，它原来属于（或不属于）相等子图，现在仍属于（或不属于）相等子图。
• XX 集一端在 S'S​′​​ 中， YY 端在 TT 中的边 e(i \rightarrow j)e(i→j)，它的 l_{i}, l_{j}l​i​​,l​j​​ 的值有所增大。它原来不属于相等子图，现在仍不可能属于相等子图。
• XX 集一端在 SS 中，YY 端在 T'T​′​​ 中的边 e(i \rightarrow j)e(i→j)，它的 l_{i}, l_{j}l​i​​,l​j​​ 的值有所减小。也就说，它原来不属于相等子图，现在可能进入了相等子图，因而使相等子图得到了扩大。

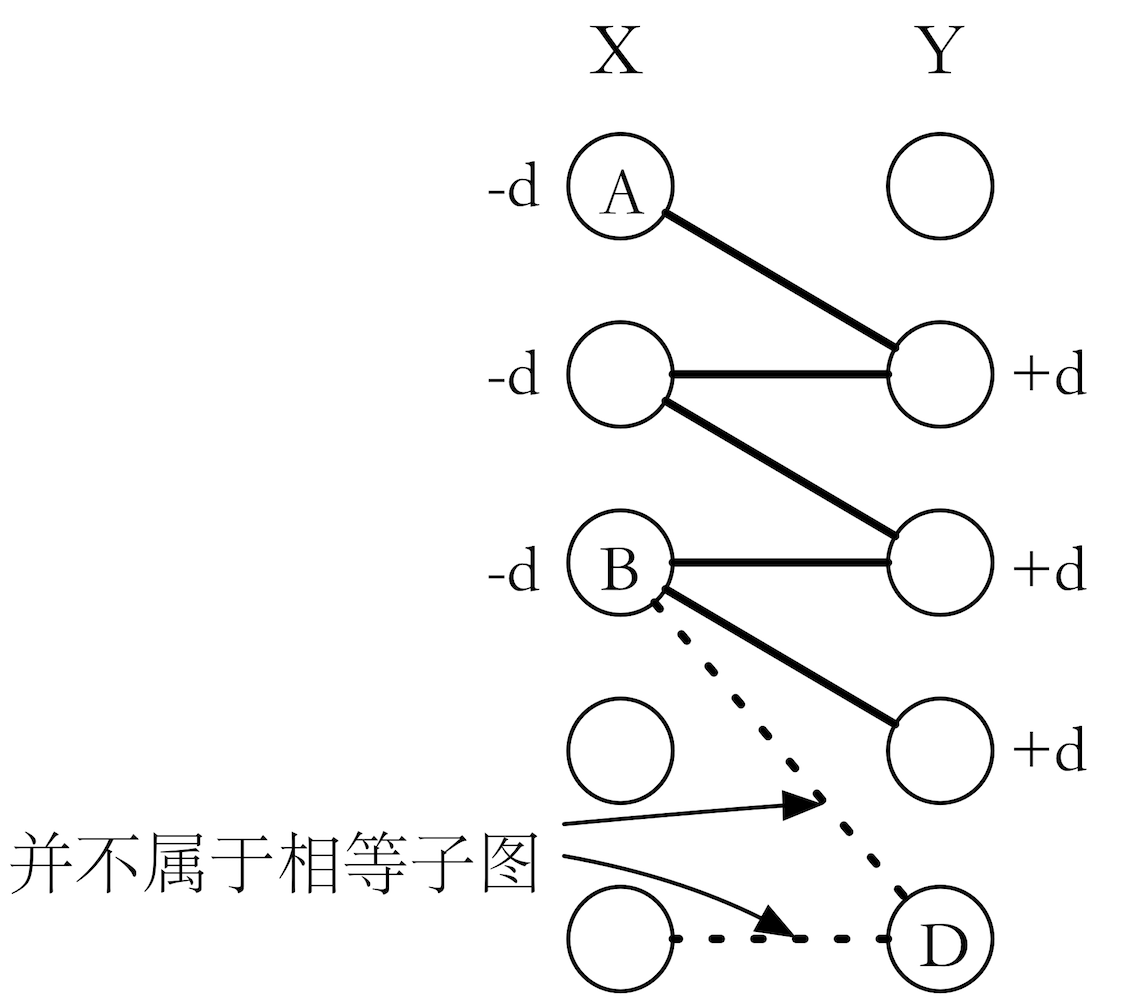
也就是说，只有 XX 集一端在 SS 中，YY 端在 T'T​′​​ 中的边才有可能被选中。继续贪心，我们只能让满足条件的边权最大的边被选中，即满足 l_{x} + l_{y} = W_{e}l​x​​+l​y​​=W​e​​，那么这个 dd 值，就应该取 d = \min\{l_{x} + l_{y} - W_{e(x\rightarrow y)}\ \vert \ x \in S, y \in T'\}d=min{l​x​​+l​y​​−W​e(x→y)​​ ∣ x∈S,y∈T​′​​}。
于是有新的边加入相等子图，我们可以愉快的继续对于未匹配顶点 uu 寻找增广路，这样的修改最多进行 nn 次，而一共有 nn 个点，所以除去修改顶标的时间，复杂度已经达到 O(n^{2})O(n​2​​)。因此算法的复杂度主要取决于修改顶标的时间。
思路一：枚举所有 n^{2}n​2​​ 条边，看是否满足条件，满足条件就更新 dd 值。最直观清晰，然而总的复杂度飙升至 O(n^{4})O(n​4​​)。
思路二：对于 T'T​′​​ 的每个点 vv，定义松弛变量 slack(v) = \min\{l_{x}+l_{y} -W_{e(x\rightarrow y)}\ \vert\ x\in S\}slack(v)=min{l​x​​+l​y​​−W​e(x→y)​​ ∣ x∈S}，这个松弛变量在匹配的过程中就可以更新，修改顶标的过程中 d = \min\{slack(v)\ \vert\ v \in T'\}d=min{slack(v) ∣ v∈T​′​​}。总复杂度 O(n^{3})O(n​3​​)，但不是严格的（想一想为什么）？但实际已经够用。
KM 算法仅仅只适用于找二分图最佳完美匹配，如果无完美匹配，那么算法很可能陷入死循环（如果不存在的边为 -INF 的话就不会，但正确性就无法保证了），对于这种情况要小心处理。
最后回顾一下总的流程，理一下思路：

1. 初始化可行顶标。
2. 用增广路定理寻对每个点找匹配。
3. 若点未找到匹配则修改可行顶标的值。
4. 重复2、3步直到所有点均有匹配为止，即找到相等子图的完美匹配为止。

模版

const int maxn = 500 + 3, INF = 0x3f3f3f3f;
int n, W[maxn][maxn];
int mat[maxn];
int Lx[maxn], Ly[maxn], slack[maxn];
bool S[maxn], T[maxn];

inline void tension(int &a, const int b) {
    if(b < a) a = b;
}

inline bool match(int u) {
    S[u] = true;
    for(int v = 0; v < n; ++v) {
        if(T[v]) continue;
        int t = Lx[u] + Ly[v] - W[u][v];
        if(!t) {
            T[v] = true;
            if(mat[v] == -1 || match(mat[v])) {
                mat[v] = u;
                return true;
            }
        }else tension(slack[v], t);
    }
    return false;
}

inline void update() {
    int d = INF;
    for(int i = 0; i < n; ++i)
        if(!T[i]) tension(d, slack[i]);
    for(int i = 0; i < n; ++i) {
        if(S[i]) Lx[i] -= d;
        if(T[i]) Ly[i] += d;
    }
}

inline void KM() {
    for(int i = 0; i < n; ++i) {
        Lx[i] = Ly[i] = 0; mat[i] = -1;
        for(int j = 0; j < n; ++j) Lx[i] = max(Lx[i], W[i][j]);
    }
    for(int i = 0; i < n; ++i) {
        fill(slack, slack + n, INF);
        while(true) {
            for(int j = 0; j < n; ++j) S[j] = T[j] = false;
            if(match(i)) break;
            else update();
        }
    }
}

  

参考目录：http://www.nocow.cn/index.php/Kuhn-Munkres%E7%AE%97%E6%B3%95 & 刘汝佳：《训练指南》