目录
0.黎曼几何
1. 欧几里得几何与黎曼几何的区别
2.黎曼流形
3.黎曼距离
4.切空间
5.黎曼均值
6. SPD矩阵如何形成黎曼流型
7.切线空间映射
8.同余变换和同余不变
9.黎曼对齐
科普性笔记,做了解,不深入。
0.黎曼几何
黎曼几何是一种基于欧几里得几何的扩展,它允许在弯曲的空间中研究几何学。黎曼几何被广泛应用于物理学、天文学、地理学、计算机科学、机器学习等领域。
在欧几里得几何中,平面上的直线是直的,而在黎曼几何中,我们允许空间中的直线是弯曲的。这种弯曲通常是由物理现象引起的,例如地球表面的曲率。
在黎曼几何中,我们可以通过定义度量来描述空间的几何结构。度量是一个函数,它测量两个点之间的距离。在欧几里得几何中,度量是标准的欧几里得距离公式,而在黎曼几何中,度量可以是一般的函数形式。黎曼度量通常定义为一个对称的正定二次型。
另外,在黎曼几何中,我们可以定义曲率来描述空间的弯曲程度。曲率度量了一个曲面的局部弯曲程度,并反映了这个曲面相对于欧几里得空间的扭曲程度。在欧几里得空间中,曲率为零,而在弯曲的空间中,曲率可以是正的、负的或零。曲率在物理学中是一个非常重要的概念,因为它描述了引力的强度和方向。
总之,黎曼几何是一种非常重要的数学分支,它扩展了我们对几何学的理解,允许我们在弯曲的空间中研究几何学,并且被广泛应用于物理学、天文学、地理学、计算机科学、机器学习等领域。
1. 欧几里得几何与黎曼几何的区别
欧几里得几何和黎曼几何是两种不同的几何学体系,它们之间的区别主要在于它们所描述的空间的性质和度量方式。
欧几里得几何是在欧氏空间中研究点、线、面及其之间关系的几何学分支,欧氏空间是一个以点、直线、平面为基本元素的空间,满足欧几里得公设。欧几里得几何的基本性质是平行公设,即给定一直线和一个点,可以在该直线上唯一确定一条与该直线平行的直线。
黎曼几何是一种更为广义的几何学,它研究的空间不一定满足欧几里得公设,而是由一个叫做度量的概念所描述的空间。在黎曼几何中,空间被看作是由一个叫做度量张量的对象所描述的,它可以用来测量空间中点之间的距离和角度。与欧几里得几何不同的是,在黎曼几何中,平行公设不再成立,而是被一个叫做测地线的概念所取代。测地线是空间中一条“最短”的路径,它不一定是直线,而是根据度量张量而定的曲线。
简单来说,欧几里得几何研究的是欧氏空间中的几何性质,主要考虑点、线、面之间的关系以及它们之间的距离和角度;而黎曼几何则研究更为广义的空间,在这样的空间中可以有不同于欧氏空间的几何性质,它所考虑的是空间中点之间的距离和角度等度量概念,也涉及到测地线等特殊的几何概念。
2.黎曼流形
黎曼流形是一种数学概念,它描述了一种多维空间的结构,可以用来研究曲线、曲面、流形等几何对象的性质。
具体来说,黎曼流形是一个具有度量的连续空间,这个度量允许我们度量流形上的长度、角度和体积等几何性质。黎曼流形的度量可以用来定义距离、曲率、体积等概念,这些概念对于研究流形上的几何问题非常重要。
黎曼流形的研究在数学上有广泛的应用,尤其在数学物理中。它被用来描述广义相对论中的时空结构,也被用来研究其他物理学问题,例如弦理论、统计力学和量子场论等。除此之外,黎曼流形还在计算机科学中有着广泛的应用,例如计算机视觉、机器学习和图形学等领域。
3.黎曼距离
黎曼距离是定义在黎曼流形上的一种距离度量。对于两个流形上的点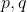 ,它们之间的黎曼距离
,它们之间的黎曼距离 定义为连接它们的最短测地线(geodesic)的长度。
定义为连接它们的最短测地线(geodesic)的长度。
在黎曼流形上,测地线相当于直线的概念,是两点间最短的连线。黎曼距离的定义利用了这个概念,也就是连接两点的最短路径。
黎曼距离在很多数学和工程应用中都有广泛的应用,例如:
-
机器学习和数据分析中的度量学习:在许多数据分析问题中,我们需要寻找一种距离度量,用来衡量数据点之间的相似性。在许多高维数据集中,数据点往往具有复杂的流形结构,此时黎曼距离可以用来描述它们之间的相似性。
-
图像处理和计算机视觉中的形状比较:在形状比较问题中,我们需要比较两个对象的形状相似性。例如,在人脸识别中,我们需要比较两个人脸的形状相似性。此时,可以将人脸表示为一个黎曼流形,利用黎曼距离来比较它们之间的相似性。
-
优化算法中的约束条件:在一些优化问题中,我们需要考虑一些特定的约束条件,例如正定性、旋转不变性等。此时,可以将优化问题定义在一个黎曼流形上,并利用黎曼距离来定义约束条件。
总之,黎曼距离是一种非常重要的距离度量,在许多领域都有着广泛的应用。
4.切空间
在微积分和微分几何中,切空间是一种描述流形上点的局部线性结构的概念。对于一个 维流形上的点
维流形上的点 ,它的切空间可以被视为该点附近的所有局部线性变化的集合。在每个点
,它的切空间可以被视为该点附近的所有局部线性变化的集合。在每个点 处,切空间都是一个
处,切空间都是一个 维向量空间,它与欧几里得空间中的向量空间类似,但是它具有更加复杂的拓扑和几何结构。
维向量空间,它与欧几里得空间中的向量空间类似,但是它具有更加复杂的拓扑和几何结构。
切空间在微分几何中有着重要的应用。它可以被用来定义曲面的法向量、测地线、曲率等几何量,并且可以被用来描述一些曲面的性质,例如最大和最小曲率的值、曲面的局部形状等。此外,在机器学习和数据分析中,切空间也有着广泛的应用。例如,我们可以将一些高维数据点表示为流形上的点,并利用切空间来描述它们的局部几何结构,从而设计更加复杂的数据分析算法。
对于黎曼流形,切空间也具有重要的作用。由于黎曼流形上每个点的切空间是一个线性空间,我们可以利用它来定义各种线性运算和度量,例如内积、范数、平均值等。这些概念可以被用来构建各种机器学习和优化算法,用于处理具有黎曼流形结构的数据集。
5.黎曼均值
在黎曼流形上,我们可以定义一组数据点的均值,称为黎曼均值(Riemannian mean)或黎曼中心(Riemannian centroid)。黎曼均值是一组数据点在黎曼流形上的中心点,它可以被视为一组数据点的代表点。
在欧几里得空间中,均值可以通过简单地求平均值来计算。但是,在黎曼流形中,由于每个点的切空间是一个不同的线性空间,因此不能直接对坐标求平均值来计算均值。相反,我们需要通过一些特定的算法来计算黎曼均值。
黎曼均值的计算对许多数据分析和机器学习问题非常重要,例如聚类、分类和降维等。例如,在图像处理和计算机视觉中,我们经常需要对一组图像进行处理和分析,此时可以利用黎曼均值来计算这些图像的平均形状和特征。
除了黎曼均值之外,黎曼流形上还有许多其他的统计量和运算,例如黎曼方差、黎曼中心散步矩阵等。这些概念可以被用于构建更加复杂的统计模型和算法,用来处理具有流形结构的数据集。
在黎曼流形上,计算均值的方法不同于欧几里得空间中简单的求平均值。在黎曼流形上,我们可以使用迭代算法来计算均值。以下是一种常见的迭代算法,称为Riemannian Trust-Region (RTR) 方法:
-
初始化:选择任意一个数据点作为起始点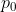 ,并选择一个初始的半径
,并选择一个初始的半径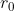 。
。
-
迭代:对于每个迭代步骤k,进行以下操作:
a. 计算所有数据点与当前点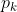 之间的距离,使用黎曼度量来度量距离。
之间的距离,使用黎曼度量来度量距离。
b. 将距离转化为权重,权重值为距离的倒数的平方。
c. 使用加权平均法计算一个新的均值 ,其中每个数据点的权重是在上一步中计算的权重。
,其中每个数据点的权重是在上一步中计算的权重。
d. 计算当前点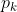 与新均值
与新均值 之间的距离
之间的距离 ,使用黎曼度量来度量距离。
,使用黎曼度量来度量距离。
e. 如果 小于半径
小于半径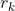 ,则接受新的均值
,则接受新的均值 ,并将半径更新为
,并将半径更新为 ;否则,拒绝新的均值
;否则,拒绝新的均值 ,并将半径更新为
,并将半径更新为
f. 重复步骤b-e,直到收敛到一个稳定的均值p。
这种方法是一种基于迭代的局部搜索算法,它通过逐步改进均值来找到一组数据点的黎曼均值。由于黎曼流形上的度量是非线性的,因此这种方法需要进行多次迭代才能收敛到稳定的均值。此外,为了保证算法的收敛性和数值稳定性,需要进行一些额外的约束和调整,例如限制迭代步数、控制半径的大小、避免出现数值不稳定等。
除了RTR方法之外,还有许多其他的方法可以用来计算黎曼均值,例如黎曼梯度下降法、黎曼牛顿法、黎曼平均值算法等。
6. SPD矩阵如何形成黎曼流型
SPD(Symmetric Positive Definite)矩阵是指对称正定矩阵。
一个n阶对称正定矩阵的集合可以表示为 。对于任意的
。对于任意的 和
和 ,定义如下映射:
,定义如下映射:
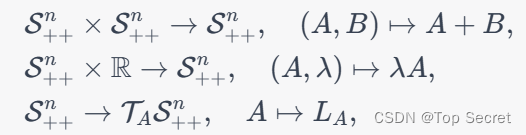
其中 是一个从
是一个从 到
到 的映射。这个映射定义了一个切空间
的映射。这个映射定义了一个切空间 ,它在每个点
,它在每个点 上都是一个
上都是一个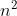 维的向量空间。
维的向量空间。
接下来,我们定义一个内积 在每个切空间
在每个切空间 上:
上:
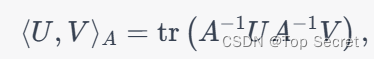
其中 。这个内积定义了一个黎曼度量,使得
。这个内积定义了一个黎曼度量,使得 成为了一个黎曼流形。
成为了一个黎曼流形。
需要注意的是,这个黎曼度量是依赖于矩阵A的。也就是说,在 上的不同点处,黎曼度量会有所不同。这个事实反映了黎曼流形的一般性质,即流形上的度量可以随着位置而变化。
上的不同点处,黎曼度量会有所不同。这个事实反映了黎曼流形的一般性质,即流形上的度量可以随着位置而变化。
总之,SPD矩阵上定义的内积和流形结构是如此定义的:首先定义一个切空间,然后定义一个内积,最终得到了一个黎曼流形。
7.切线空间映射
切线空间映射是一种将高维流形中的点映射到其切空间上的方法,通常也称为切映射或切空间投影。
首先,切线空间是指流形上某一点处的切向量所构成的线性空间,也就是该点处的切空间。在微积分中,切向量是描述曲线在该点附近的切线方向的概念。在高维流形上,切向量可以被看作是描述流形在该点处切平面上的切向量。
切线空间映射将一个流形上的点映射到该点处的切空间上,其具体实现方式通常涉及到微积分和线性代数中的概念。在欧几里得空间中,我们可以通过求取该点处的导数或者 Jacobian 矩阵来计算该点处的切空间映射。在黎曼几何中,我们需要借助度量张量来定义切向量,并利用切向量的内积和度量张量来定义切空间的结构。
切线空间映射在机器学习和计算机视觉中有广泛的应用。例如,在流形学习中,切线空间映射可以用来将高维数据嵌入到低维流形中,以便进行数据降维和可视化。在计算机视觉中,切线空间映射可以用来计算图像的梯度和特征,以实现图像分割、目标检测等任务。此外,切线空间映射还可以用来计算流形上的平均值、中心点和曲线等几何概念,以便对流形数据进行聚类和分类。
8.同余变换和同余不变
在黎曼几何中,同余变换指的是保持度量不变的变换。也就是说,给定一个黎曼空间  和一个同余变换
和一个同余变换  ,则对于该空间中任意两点
,则对于该空间中任意两点  ,有
,有  ,其中
,其中  是使用度量张量 g 计算的两点之间的距离。
是使用度量张量 g 计算的两点之间的距离。
同余变换是黎曼几何中的一个重要性质,它保证了黎曼空间的几何结构在同余变换下不会改变。这一性质可以帮助我们理解和比较不同的黎曼空间,并将它们之间的几何性质进行比较和分类。
同余不变是指同余变换下不变的量,通常包括黎曼曲率张量、黎曼体积元、黎曼联络等。这些量在同余变换下具有不变性,也就是说,它们的值在同余变换下保持不变。同余不变性质是黎曼几何中的一个重要性质,它使得我们能够对黎曼流形进行刻画和比较,并在实际应用中使用黎曼几何的工具和技术。
黎曼空间中的同余变换和同余不变性质在计算机视觉和机器学习中有广泛的应用。例如,在计算机视觉中,同余变换可以用来生成对抗样本和数据增强,以提高深度学习模型的鲁棒性和泛化性能。同余不变性质则可以用来设计具有旋转、平移和缩放不变性的特征和模型,以便在处理自然图像和视频数据时获得更好的性能和效果。
9.黎曼对齐
黎曼对齐(Riemannian alignment)是一种基于黎曼几何的数据对齐方法,它可以将数据点从一个黎曼流形变换到另一个黎曼流形,以便进行比较和分析。
黎曼对齐的主要思想是将数据点从一个流形映射到另一个流形,使得它们在新流形上的位置和结构尽可能相似。具体来说,黎曼对齐分为两个步骤:
-
流形配准(Manifold Registration):将待配准的两个黎曼流形中的一些点对应起来,以便进行对齐。这一步通常使用一些特定的算法来实现,例如基于距离度量的配准方法、基于特征的配准方法、基于变形模型的配准方法等。
-
流形变换(Manifold Transformation):利用配准结果将待对齐的数据点从一个流形变换到另一个流形。在黎曼几何中,流形变换通常使用黎曼流形上的切空间或切空间的扩展来实现。具体来说,可以使用切空间中的切向量和黎曼流形上的黎曼联络来定义流形变换的方向和大小。
黎曼对齐在计算机视觉、机器学习和图像处理等领域中有广泛的应用,例如人脸识别、图像对齐、形状分析、变形建模等。它能够有效地处理具有非欧几里得结构的数据,并且可以提高数据分析的准确性和可靠性。
本文内容由网友自发贡献,版权归原作者所有,本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容,请联系:hwhale#tublm.com(使用前将#替换为@)