目录
写在前面
机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理;“广”在分析多个机器学习模型:决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。
1 什么是线性判别分析?
线性判别分析(Linear Discriminant Analysis, LDA) 的核心思想是: 将给定训练集投影到特征空间的一个超平面上,并设法使同类样本投影点尽可能接近,异类样本投影点尽可能远离 。
线性判别分析是一种将样本投影到低维空间进行分类的方法,因此它既是分类技术又是降维技术,本文主要讨论LDA进行分类的原理:在对新样本进行分类时,将其投影到同样的分类平面上,根据投影点的位置确定新样本的类别
如图所示是LDA算法分类的直观图示,很显然右图分类效果更好,接下来我们讨论如何找到超平面实现以下两个目标:
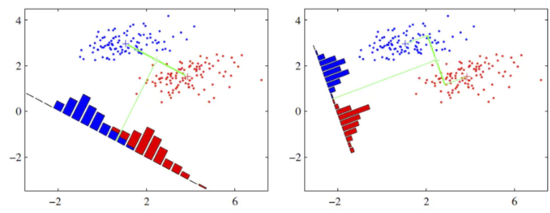
2 协方差与协方差矩阵
LDA算法的实现离不开样本协方差矩阵,本节简单介绍什么是协方差和协方差矩阵。
协方差(covariance) 定义为
c o v ( x 1 , x 2 ) = E [ ( x 1 − E [ x 1 ] ) ( x 2 − E [ x 2 ] ) ] cov\left( x_1,x_2 \right) =\mathbb{E} \left[ \left( x_1-\mathbb{E} \left[ x_1 \right] \right) \left( x_2-\mathbb{E} \left[ x_2 \right] \right) \right] co v ( x 1 , x 2 ) = E [ ( x 1 − E [ x 1 ] ) ( x 2 − E [ x 2 ] ) ]
其中 x 1 x_1 x 1 与 x 2 x_2 x 2 是随机变量。 协方差反映随机变量间的相关情况,协方差越大表明随机变量变化趋势越接近,相关性越强 。特别地,当 x 1 = x 2 x_1=x_2 x 2 时协方差退化为方差,反映随机变量自身变化的稳定性。
样本协方差 是在给定样本集的情况下对协方差的无偏估计量
c o v ( x 1 , x 2 ) = 1 n − 1 ∑ i = 1 n ( x 1 ( i ) − x ˉ 1 ) ( x 2 ( i ) − x ˉ 2 ) cov\left( x_1,x_2 \right) =\frac{1}{n-1}\sum_{i=1}^n{\left( x_{1}^{\left( i \right)}-\bar{x}_1 \right) \left( x_{2}^{\left( i \right)}-\bar{x}_2 \right)} co v ( x 1 , x 2 ) = i = 1 ∑ n ( x 1 ( i ) − x ˉ 1 ) ( x 2 ( i ) − x ˉ 2 )
为便于计算通常将样本集 X X X 中心化,即使样本均值为0,记 X ~ = [ x ~ ( 1 ) x ~ ( 2 ) ⋯ x ~ ( n ) ] \boldsymbol{\tilde{X}}=\left[ \begin{matrix} \boldsymbol{\tilde{x}}^{\left( 1 \right)}& \boldsymbol{\tilde{x}}^{\left( 2 \right)}& \cdots& \boldsymbol{\tilde{x}}^{\left( n \right)}\\\end{matrix} \right] [ x ~ ( 1 ) x ~ ( 2 ) ⋯ x ~ ( n ) ] ,其中样本都为中心化样本,此时协方差矩阵可写为
C = 1 n − 1 X ~ X ~ T C=\frac{1}{n-1}\boldsymbol{\tilde{X}\tilde{X}}^T X ~ X ~ T

如图所示为不同协方差矩阵情况下的样本分布情况。方差大小决定了数据在特征方向上的聚合情况—— 方差越大,数据在该特征方向分布越散 ;协方差决定了两个原始维度的相关性, 协方差越大,原始维度相关性越强
3 LDA原理推导
3.1 约束条件
在二分类问题上,设训练集中两个类别样本集、样本中心、协方差矩阵分别为 X k \boldsymbol{X}_k X k 、 μ k \boldsymbol{\mu }_k μ k 、 Σ k \boldsymbol{\varSigma }_k Σ k ( k = 0 , 1 ) (k=0,1) ( k = 0 , 1 ) 。要使同类样本尽可能接近,即使同类样本投影点的协方差尽可能小
w = a r g min w ∑ x ∈ X k ( w T x − w T μ k ) ( w T x − w T μ k ) T = a r g min w w T Σ k w \boldsymbol{w}=\underset{\boldsymbol{w}}{\mathrm{arg}\min}\sum_{\boldsymbol{x}\in \boldsymbol{X}_k}{\left( \boldsymbol{w}^T\boldsymbol{x}-\boldsymbol{w}^T\boldsymbol{\mu }_k \right) \left( \boldsymbol{w}^T\boldsymbol{x}-\boldsymbol{w}^T\boldsymbol{\mu }_k \right) ^T}=\underset{\boldsymbol{w}}{\mathrm{arg}\min}\boldsymbol{w}^T\boldsymbol{\varSigma }_k\boldsymbol{w} w arg min x ∈ X k ∑ ( w T x − w T μ k ) ( w T x − w T μ k ) T = w arg min w T Σ k w
我们从协方差的物理意义上思考一下为什么协方差小同类样本就接近。如下图所示,是同一个三维样本在两个二维平面的投影,结合第二节对协方差的介绍,可以看出协方差大的样本越细长分散,协方差小则反之。所以协方差小可以使样本更聚合,也即样本投影点尽可能接近。
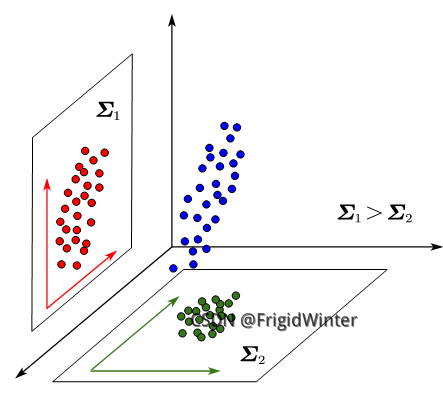
要使异类样本投影点尽可能远离,即使异类中心投影尽可能远离
w = a r g max w ∥ w T μ 0 − w T μ 1 ∥ 2 2 = a r g max w w T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w \boldsymbol{w}=\underset{\boldsymbol{w}}{\mathrm{arg}\max}\left\| \boldsymbol{w}^T\boldsymbol{\mu }_0-\boldsymbol{w}^T\boldsymbol{\mu }_1 \right\| _{2}^{2}=\underset{\boldsymbol{w}}{\mathrm{arg}\max }\boldsymbol{w}^T\left( \boldsymbol{\mu }_0-\boldsymbol{\mu }_1 \right) \left( \boldsymbol{\mu }_0-\boldsymbol{\mu }_1 \right) ^T\boldsymbol{w} w arg max ∥ ∥ w T μ 0 − w T μ 1 ∥ ∥ 2 2 = w arg max w T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w
在同类样本聚合的基础上,中心样本的相斥直观上会使异类样本集合互相远离
3.2 数值优化
注意到前面提到的两个约束条件优化方向相反——一个要求最大,一个要求最小,因此我们可以将目标函数综合为
w ∗ = a r g max w J ( w ) , J ( w ) = w T S b w w T S w w \boldsymbol{w}^*=\underset{\boldsymbol{w}}{\mathrm{arg}\max}J\left( \boldsymbol{w} \right) , J\left( \boldsymbol{w} \right) =\frac{\boldsymbol{w}^T\boldsymbol{S}_b\boldsymbol{w}}{\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}} w arg max J ( w ) , J ( w ) = w T S w w w T S b w
其中 S w = Σ 0 + Σ 1 \boldsymbol{S}_w=\boldsymbol{\varSigma }_0+\boldsymbol{\varSigma }_1 Σ 1 称为 类内散度矩阵(within-class scatter matrix) , S b = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T \boldsymbol{S}_b=\left( \boldsymbol{\mu }_0-\boldsymbol{\mu }_1 \right) \left( \boldsymbol{\mu }_0-\boldsymbol{\mu }_1 \right) ^T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T 称为 类间散度矩阵(between-class scatter matrix) 。名字起什么不重要,这个目标函数的本质就是两个约束条件之比。
值得注意的是,优化可行解在直线 α w ∗ \alpha \boldsymbol{w}^* α w ∗ 上,可以不失一般性地约束 w T S w w = 1 \boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}=1 w T S w w = 1 ,从而优化问题转变为
{ w ∗ = a r g min w − w T S b w s . t . w T S w w = 1 \begin{cases} \boldsymbol{w}^*=\underset{\boldsymbol{w}}{\mathrm{arg}\min}\,\,-\boldsymbol{w}^T\boldsymbol{S}_b\boldsymbol{w}\\ \mathrm{s}.\mathrm{t}. \boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}=1\\\end{cases} ⎩ ⎨ ⎧ w ∗ = w arg min − w T S b w s . t . w T S w w = 1
由拉格朗日乘子法设拉格朗日函数 L ( w , λ ) = − w T S b w + λ ( w T S w w − 1 ) L\left( \boldsymbol{w}, \lambda \right) =-\boldsymbol{w}^T\boldsymbol{S}_b\boldsymbol{w}+\lambda \left( \boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}-1 \right) L ( w , λ ) = − w T S b w + λ ( w T S w w − 1 ) ,则
∂ L ( w , λ ) ∂ w = − 2 S b w + 2 λ S w w = 0 ⇒ S w − 1 S b w ∗ = λ w ∗ \frac{\partial L\left( \boldsymbol{w}, \lambda \right)}{\partial \boldsymbol{w}}=-2\boldsymbol{S}_b\boldsymbol{w}+2\lambda \boldsymbol{S}_w\boldsymbol{w}=0\Rightarrow \boldsymbol{S}_{w}^{-1}\boldsymbol{S}_b\boldsymbol{w}^*=\lambda \boldsymbol{w}^* ∂ w ∂ L ( w , λ ) = − 2 S b w + 2 λ S w w = S w − 1 S b w ∗ = λ w ∗
考虑到 S w − 1 S b w ∗ = S w − 1 ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w ∗ \boldsymbol{S}_{w}^{-1}\boldsymbol{S}_b\boldsymbol{w}^*=\boldsymbol{S}_{w}^{-1}\left( \boldsymbol{\mu }_0-\boldsymbol{\mu }_1 \right) \left( \boldsymbol{\mu }_0-\boldsymbol{\mu }_1 \right) ^T\boldsymbol{w}^* S w − 1 S b w ∗ = S w − 1 ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w ∗ ,其中 ( μ 0 − μ 1 ) T w ∗ \left( \boldsymbol{\mu }_0-\boldsymbol{\mu }_1 \right) ^T\boldsymbol{w}^* ( μ 0 − μ 1 ) T w ∗ 是常数,因此 w ∗ \boldsymbol{w}^* w ∗ 与 S w − 1 ( μ 0 − μ 1 ) \boldsymbol{S}_{w}^{-1}\left( \boldsymbol{\mu }_0-\boldsymbol{\mu }_1 \right) S w − 1 ( μ 0 − μ 1 ) 共线,前面说到这一条线上的解都是可行的最优解,所以可选择
w ∗ = S w − 1 ( μ 0 − μ 1 ) {\boldsymbol{w}^*=\boldsymbol{S}_{w}^{-1}\left( \boldsymbol{\mu }_0-\boldsymbol{\mu }_1 \right) } w ∗ = S w − 1 ( μ 0 − μ 1 )
4 Python实现
4.1 计算类内散度矩阵
根据定义 S w = Σ 0 + Σ 1 \boldsymbol{S}_w=\boldsymbol{\varSigma }_0+\boldsymbol{\varSigma }_1 Σ 1 编程
<span style="color:#444444"><span style="background-color:#f6f6f6"><span style="color:#333333"><strong>def</strong></span> <span style="color:#880000"><strong>__calSw</strong></span>(<span style="color:#333333"><strong>self</strong></span>):
<span style="color:#888888"># 类样本数</span>
N1, N2 = np.size(<span style="color:#333333"><strong>self</strong></span>.X1, <span style="color:#880000">1</span>), np.size(<span style="color:#333333"><strong>self</strong></span>.X2, <span style="color:#880000">1</span>)
<span style="color:#888888"># 类协方差矩阵</span>
sigma1 = np.zeros((np.size(<span style="color:#333333"><strong>self</strong></span>.X, <span style="color:#880000">0</span>), np.size(<span style="color:#333333"><strong>self</strong></span>.X, <span style="color:#880000">0</span>)))
sigma2 = np.zeros((np.size(<span style="color:#333333"><strong>self</strong></span>.X, <span style="color:#880000">0</span>), np.size(<span style="color:#333333"><strong>self</strong></span>.X, <span style="color:#880000">0</span>)))
<span style="color:#333333"><strong>for</strong></span> i <span style="color:#333333"><strong>in</strong></span> range(N1):
sigma1 = sigma1 + (<span style="color:#333333"><strong>self</strong></span>.X1[<span style="color:#bc6060">:</span>, i] - <span style="color:#333333"><strong>self</strong></span>.miu1).dot(
(<span style="color:#333333"><strong>self</strong></span>.X1[<span style="color:#bc6060">:</span>, i] - <span style="color:#333333"><strong>self</strong></span>.miu1).T)
<span style="color:#333333"><strong>for</strong></span> i <span style="color:#333333"><strong>in</strong></span> range(N2):
sigma2 = sigma2 + (<span style="color:#333333"><strong>self</strong></span>.X2[<span style="color:#bc6060">:</span>, i] - <span style="color:#333333"><strong>self</strong></span>.miu2).dot(
(<span style="color:#333333"><strong>self</strong></span>.X2[<span style="color:#bc6060">:</span>, i] - <span style="color:#333333"><strong>self</strong></span>.miu2).T)
<span style="color:#333333"><strong>return</strong></span> sigma1 + sigma2</span></span>
4.2 计算模型参数
根据公式 w ∗ = S w − 1 ( μ 0 − μ 1 ) {\boldsymbol{w}^*=\boldsymbol{S}_{w}^{-1}\left( \boldsymbol{\mu }_0-\boldsymbol{\mu }_1 \right) } w ∗ = S w − 1 ( μ 0 − μ 1 ) 编程
<span style="color:#444444"><span style="background-color:#f6f6f6"><span style="color:#888888"># 类均值向量</span>
<span style="color:#333333"><strong>self</strong></span>.miu1 = np.mean(<span style="color:#333333"><strong>self</strong></span>.X1, <span style="color:#880000">1</span>).reshape(-<span style="color:#880000">1</span>, <span style="color:#880000">1</span>)
<span style="color:#333333"><strong>self</strong></span>.miu2 = np.mean(<span style="color:#333333"><strong>self</strong></span>.X2, <span style="color:#880000">1</span>).reshape(-<span style="color:#880000">1</span>, <span style="color:#880000">1</span>)
<span style="color:#888888"># 权重参数 [w1, w2, ..., wd]^T</span>
<span style="color:#333333"><strong>self</strong></span>.w = np.linalg.inv(<span style="color:#333333"><strong>self</strong></span>.Sw).dot(<span style="color:#333333"><strong>self</strong></span>.miu1 - <span style="color:#333333"><strong>self</strong></span>.miu2)</span></span>
4.3 可视化
采用西瓜数据集进行本次LDA实验数据,可视化如下

今天就到这啦!关注我,后续更多有趣学习知识哦~
本文内容由网友自发贡献,版权归原作者所有,本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容,请联系:hwhale#tublm.com(使用前将#替换为@)