模式识别：最小错误率贝叶斯决策分类

2023-05-16

一、引言

1.用贝叶斯决策理论分类要事先知道两个条件及要求：

①.各类的先验概率： $P(w_i)$

及特征向量的条件概率密度： $p(x|w_i)$

或后验概率： $P(w_i|x)$

②.决策分类的类别一定

2.解决的问题：

已知一定数目的样本，设计分类器，对未知样本进行分类。

3.基于样本的两步贝叶斯决策

①首先根据样本估计 $P(w_i)$ 和 $p(x|w_i)$

记为 $\widehat{P}(w_i)$ 和 $\widehat{p}(x|w_i)$

②然后用估计的概率密度设计贝叶斯分类器

前提：训练样本的分布能代表样本的真实分布。每个样本集中的样本都是所谓独立同分布的随机变量，且有充分的训练样本

假设：当样本数N →∞时，如此得到的分类器收敛于理论上的最优解。即满足：

$\widehat{P}(w_i)$ → $P(w_i)$ ， $\widehat{p}(x|w_i)$ → $p(x|w_i)$

4.先验概率与条件概率密度估计

①类的先验概率估计：可依靠经验或训练数据中各类出现的频率估计，交容易实现；

②类条件概率密度的估计：概率密度函数包含了一个随机变量的全部信息，估计起来比较困难。

5.概率密度估计的两种基本方法

①参数估计：根据对问题的一般性的认识，假设随机变量服从某种分布，分布函数的参数通过训练数据来估计。如：ML 估计，Bayesian估计

②非参数估计：不用模型，而只利用训练数据本身对概率密度做估计。如：Parzen窗法，kn-近邻估计法。

下面只着重介绍参数估计

二、最大似然估计与贝叶斯参数估计

1.最大似然估计基本原理

先做以下假设：

①估计的参数记为： $\theta$ 。它是确定但未知的量（多个参数时为向量）；

②每类的样本集记作： $\chi_i$ ， $i=1,2,...,c,$

其中样本都是从密度为 $p(x|w_i)$ 的总体中独立抽取出来的，满足独立同分布条件；

③类条件概率密度 $p(x|w_i)$ 具有某种确定的函数形式，只是其中的参数 $\theta$ 未知；

④各类样本只包含本类的分布信息，不同类别的参数是独立的，这样就可以分别对每一类单独处理。

现有以下样本： $\chi=\{x_1,x_2,...,x_N\}$

有了以上假设，则获得以上样本的概率即出现样本中各个样本的联合概率是：

$l(\theta)=p(\chi|\theta)=p(x_1,x_2,...,x_N)=\prod_{i=1}^{N}{p(x_i|\theta)}$

最大似然估计，通俗的理解，即为：参数为多少时观测值出现的概率最大。

最大似然估计量： $\widehat{\theta}=arg \space max\space l(\theta)$

还可以定义对数似然函数：

$H(\theta)=lnl(\theta)=ln\prod_{i=1}^{N}{p(x_i|\theta)}=\sum_{i=1}^{N}{lnp(x_i|\theta)}$

2.最大似然估计的求解

①若待估参数为一维变量，即待估参数只有一个，其最大似然估计量就是如下微分方程的解：

$\frac{dl(\theta)}{d\theta}=0$ 或 $\frac{dH(\theta)}{d\theta}=0$

当待估参数为多个未知参数组成的向量时，即： $\theta=[\theta_1;...;\theta_s]$

求解似然函数的最大值就需要对该参数的每一维分别求导，即用下面的梯度算子：

$\nabla_\theta=[\frac{\partial}{\partial\theta_1};...,\frac{\partial}{\partial\theta_s}]$

$\nabla_\theta{l(\theta)}=0$ 或

$\nabla_\theta{H(\theta)}=\sum_{i=1}^{N}{\nabla_\theta{lnp(x_i|\theta)}}=0$

3.正态分布下的最大似然估计

仅以单变量正态分布情况估计其均值与方差： $\theta=[\theta_1;\theta_2]=[\mu;\sigma^2]$

单变量正态分布如下：

$p(x|\theta)=\frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{1}{2}(\frac{x-\mu}{\sigma})^2]$

从上述正太分布式可以得到：

$lnp(x_k|\theta)=-\frac{1}{2}ln2\pi\theta_2-\frac{1}{2\theta_2}(x_k-\theta_1)^2$

分别对两个位置参数求偏导，得到：

$\nabla_\theta{lnp(x_k|\theta)}=[\frac{1}{\theta_2}(x_k-\theta_1);-\frac{1}{2\theta_2}+\frac{1}{2\theta_2^2}(x_k-\theta_1)^2]$

最大似然估计应该是以下方程组的解：

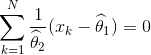$\sum_{k=1}^{N}\frac{1}{\widehat\theta_2}(x_k-\widehat\theta_1)=0$ 与 $-\sum_{k=1}^{N}\frac{1}{\widehat\theta_2}+\sum_{k=1}^{N}\frac{(x_k-\widehat\theta_1)^2}{\widehat\theta_2^2}=0$

解得：

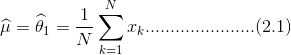
$\widehat\mu=\widehat\theta_1=\frac{1}{N}\sum_{k=1}^{N}x_k......................(2.1)$

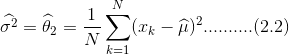
$\widehat{\sigma^2}=\widehat\theta_2=\frac{1}{N}\sum_{k=1}^{N}(x_k-\widehat\mu)^2..........(2.2)$

ML估计总结：

①简单性

②收敛性：无偏或者渐近无偏

③如果假设的类条件概率模型正确，则通常能获得较好的结果。但果假设模型出现偏差，将导致非常差的估计结果。

4.贝叶斯估计基本原理

可以把概率密度函数的参数估计问题看作一个贝叶斯决策问题，但这里决策的不是离散类别，而是参数的值，是在连续空间里做的决策。

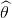
在用于分类的贝叶斯决策中，最优的条件可以是最小错误率或者最小风险。对连续变量： $\theta$ ，我们假定把它估计为： $\widehat\theta$

所带来的损失函数为： $\lambda(\widehat\theta,\theta)$

定义在样本x下的条件风险为： $R(\widehat\theta|x)=\int_{\Theta}{\lambda(\widehat\theta,\theta)}p(\theta|x)d\theta$

则估计时总期望风险为： $R=\int_{E^d}{R(\widehat\theta|x)}p(x)dx$

现在的目标是对期望风险求最小，而条件风险都是非负的，求期望风险最小就等价于对所有可能的x求条件风险最小。在有限样本集合的情况下，我们所作的就是对所有的样本求条件风险最小，即： $\theta^*=arg \space \min_{\widehat\theta}\space R(\widehat\theta|\chi)=\int_{\Theta}{\lambda(\widehat\theta,\theta)}p(\theta|\chi)d\theta$

在决策分类时，需要事先定义决策表即损失表，连续情况下需要定义损失函数，最常用的损失函数是平方误差损失函数，即： $\lambda(\widehat\theta,\theta)=(\theta-\widehat\theta)^2$

可以证明，如果采用平方误差损失函数，则θ 的贝叶斯估计量θ*是在给定x 时θ 的条件期望，即： $\theta^*=E[\theta|x]=\int_{\Theta}{\theta}p(\theta|x)d\theta$

在许多情况下 ,最小方差贝叶斯估计是最理想的，是贝叶斯的最优估计。

5.求贝叶斯估计的方法：（平方误差损失下）

①确定未知参数θ的先验分布密度 p(θ)

②求样本集的联合分布： $p(\chi|\theta)=\prod_{i=1}^{N}{p(x_i|\theta)}$

③利用贝叶斯公式求θ的后验概率分布： $p(\theta|\chi)=\frac{p(\chi|\theta)p(\theta)}{\int_{\Theta}p(\chi|\theta)p(\theta)d\theta}$

④求θ的贝叶斯估计量是： $\theta^*=\int_{\Theta}{\theta}p(\theta|\chi)d\theta$

6.正态分布时的贝叶斯估计

以最简单的一维正态分布模型为例来说明贝叶斯估计的应用。假设均值u为待估计参数，方差为已知。

均值u的先验分布也是正态分布，即： $p(\mu)=\frac{1}{\sqrt{2\pi}\sigma_0}exp[-\frac{1}{2}(\frac{\mu-\mu_0}{\sigma_0})^2]$

求μ的后验概率： $p(\mu|\chi)=\frac{p(\chi|\mu)p(\mu)}{\int_{\Theta}p(\chi|\mu)p(\mu)d\mu}$

分母只是用来对估计的后验概率进行归一化的常数项，可以暂时不考虑：

$p(\mu|\chi)=\alpha\space p(\chi|\mu)p(\mu)=\alpha\space \frac{1}{\sqrt{2\pi}\sigma_0}exp[-\frac{1}{2}(\frac{\mu-\mu_0}{\sigma_0})^2]\prod_{i=1}^{N}{ \frac{1}{\sqrt{2\pi}\sigma}exp[-\frac{1}{2}(\frac{x_i-\mu}{\sigma})^2]}$

整理得：

$p(\mu|\chi)=\alpha^,\space exp(-\frac{1}{2}((\frac{N}{\sigma^2}+\frac{1}{\sigma_0^2})\mu^2-2(\frac{1}{\sigma^2}\sum_{k=1}^{N}x_i+\frac{\mu_0}{\sigma_0^2})\mu)))=\frac{1}{\sqrt{2\pi}\sigma_N}exp[-\frac{1}{2}(\frac{\mu-\mu_N}{\sigma_N})^2]$

由两式指数项中对应的系数相等得：

$\frac{1}{\sigma_N^2}=\frac{N}{\sigma^2}+\frac{1}{\sigma_0^2}$ 与 $\frac{\mu_N}{\sigma_N^2}=\frac{N}{\sigma^2}\widehat\mu_N+\frac{\mu_N}{\sigma_0^2}$

其中， $\widehat\mu_N=\frac{1}{N}\sum_{i=1}^{N}x_i$

求解上述方程组得：

$\mu_N=\frac{N\sigma_0^2}{N\sigma_0^2+\sigma^2}\widehat\mu_N+\frac{\sigma^2}{N\sigma_0^2+\sigma^2}\mu_0$

$\sigma_N^2=\frac{\sigma^2\sigma_0^2}{N\sigma_0^2+\sigma^2}$

求μ的贝叶斯估计值：μ 的期望

$\widehat\mu=\int{\mu}p(\mu|\chi)d\mu=\int{\mu}\frac{1}{\sqrt{2\pi}\sigma_N}exp[-\frac{1}{2}(\frac{\mu-\mu_N}{\sigma_N})^2]d\mu=\mu_N$

①样本数目趋于无穷大时，第一项的系数趋于1，第二项系数趋于0，则估计的均值就是样本的算术平均，这与最大似然估计一致。

②当样本数目有限，若先验知识非常确定，则先验分布的方差就很小，则第一项系数就很小，第二项系数接近1，则估计主要由先验知识决定。

一般情况下，均值得贝叶斯估计是样本算术平均与先验分布均值之间进行加权平均。

总结：通过观察数据集X ,将先验概率密度P(θ) 转化为后验概率密度 P(θ|X) ，并期望其在真实的θ 值处有一个尖峰

7.ML估计和Bayesian估计的比较

①ML估计

1.参数为未知确定变量

2.没有利用参数先验信息

3.估计的概率模型与假设模型一致

4.可理解性好

5.计算简单

②Bayesian估计

1.参数为未知随机变量

2.利用参数的先验信息

3.估计的概率模型相比于假设模型会发生变化

4.可理解性差

5.计算复杂

三、分类器设计

1.常用概念

c类分类决策问题：按决策规则把d维特征空间分为为c个决策区域。

决策面：划分决策域的边界面称为决策面，数学上用决策面方程表示。

判别函数：表达决策规则的函数，称为判别函数。

2.具体的判别函数、决策面方程、分类器设计

①定义一组判别函数： $g_i(x) \space\space\space i=1,2,...,c$

根据决策规则： $g_i(x)>g_j(x) \space\space j\neq i$ ，即： $g_i(x)=\max_{j=1,2,...,c}g_j(x) \space\space x\epsilon w_i$

例如基于最小错误率贝叶斯判决规则，判别函数可定义为：

$g_i(x)=P(w_i|x)\space or \space g_i(x)=p(x|w_i)p(w_i) \space or \space g_i(x)=lnp(x|w_i)+lnp(w_i)$

②决策面方程

类型w i 与w j 的区域相邻，它们之间的决策面方程为： $g_i(x)=g_j(x)$

一维特征空间的两个决策区域（d=1），决策面为分界点；

二维特征空间的两个决策区域（d=2），决策面为曲线；

三维特征空间，分界处是曲面；d维特征空间，分界处是超曲面。

3.正态分布下的最小错误率贝叶斯判别函数和决策面

1.判别函数： $g_i(x)=p(x|w_i)p(w_i)$

其中： $p(x|w_i)$ 服从： $N(\mu_i,\Sigma{_i}) \space i=1,2,...,c$

$p(x|w_i)=\frac{1}{(2\pi)^{d/2}|\Sigma{_i}|^{1/2}}exp[-\frac{1}{2}(x-\mu_i)^T\Sigma{_i}^{-1}(x-\mu_i)]$

进行单调的对数变换，则判别函数为：

$g_i(x)=ln[p(x|w_i)p(w_i)]=-\frac{1}{2}(x-\mu_i)^T\Sigma{_i}^{-1}(x-\mu_i)-\frac{d}{2}ln2\pi-ln\frac{1}{2}|\Sigma{_i}|+lnp(w_i)$

2.决策方程：

$g_i(x)-g_j(x)=-\frac{1}{2}[(x-\mu_i)^T\Sigma{_i}^{-1}(x-\mu_i)-(x-\mu_j)^T\Sigma{_j}^{-1}(x-\mu_j)]-ln\frac{1}{2}\frac{|\Sigma{_i}|}{|\Sigma{_j}|}+ln\frac{p(w_i)}{p(w_j)}=0$

四、实验举例

1.实验内容

1.以身高为例，画出男女生身高的直方图并做对比；

2.采用最大似然估计方法，求男女生身高以及体重分布的参数；

3.采用贝叶斯估计方法，求男女生身高以及体重分布的参数（注明自己选定的参数情况）；

4.采用最小错误率贝叶斯决策，画出类别判定的决策面。并判断某样本的身高体重分别为(160,45)时应该属于男生还是女生？为(178,70)时呢？

2.具体步骤

1.通过python的xlrd包相应的库函数来读取excel文件中的数据，并将需要处理的数据存储与数组中，并通过matplotlib库函数画出男生和女生的身高分布直方图，如图一：

图一

结果分析：从图中可以看，男女生的身高分布没有完全服从正态分布，主要由于样本数量比较少。很多时候，正态分布模型是一个合理假设。在特征空间中，某类样本较多分布在这类均值附近，远离均值的样本较少，一般用正态分布模型是合理的。在后续的实验分析中都将运用正态分布特性对男女生的样本进行分析。

2.采用最大似然估计方法，求男女生身高以及体重分布的参数；

假设身高体重相互独立并且都满足正态分布，采用最大似然法估计其参数，根据公式2.1、2.2求出男女生身高和体重的均值和方差。所求得的参数如表一所示：

	女生身高	女生体重	男生身高	男生体重
均值(μ)	162.3125	50.7447	173.7388	66.0923
方差(σ2)	17.3606	21.1978	27.9827	86.5551

3.采用贝叶斯估计方法，求男女生身高以及体重分布的参数（假定方差已知，作业请注明自己选定的一些参数情况）。

特殊情况1:（先验知识可靠，样本不起作用），即

'''
特殊情况1:
variance0=0时，mean_bayes=mean0
先验知识可靠，样本不起作用
#以男生身高为例，选定参数：mean0=20,variance=10,variance0=0
'''
man_height_mean_bayes=get_mean_bayes(man_height,20,0,10)
print(man_height_mean_bayes)

结果为：20.0

特殊情况2：（先验知识十分不确定，完全依靠样本信息），即：

'''
特殊情况2:
variance0>>variance时，mean_bayes=sample_mean
先验知识十分不确定，完全依靠样本信息,结果与最大似然估计结果近似
#以女生身高为例，选定参数：mean0=50,variance=1,variance0=100
'''
woman_height_mean_bayes=get_mean_bayes(woman_height,50,100,1)
print(woman_height_mean_bayes)

结果为：162.3008019997917

4.采用最小错误率贝叶斯决策，画出类别判定的决策面。并判断某样本的身高体重分别为(160,45)时应该属于男生还是女生？为(178,70)时呢？

假设男女生身高及体重满足二维正态分布，记男生为w1，女生为w2，根据男女学生的人数比例确定先验概率: P(w1)=203/149=0.7658536585365854，P(w2)=1-P(w1)=0.23414634146341462

#求男生、女生先验概率
man_priori_probability=manlen/(manlen+womanlen)
woman_priori_probability=1-man_priori_probability

求男女生的协方差矩阵：

#①本题输入类数为2：即男生、女生；特征数为2：即身高、体重
#②求协方差矩阵
def get_covariance_matrix_coefficient(arr1,arr2):#arr1与arr2长度相等
    datalength1=len(arr1)
    datalength2=len(arr2)
    sum_temp=[]
    for i in range(datalength1):
        sum_temp.append((arr1[i]-sum(arr1)/datalength1)*(arr2[i]-sum(arr2)/datalength2))
        c12=sum(sum_temp)
    covariance_matrix_c12=c12/(datalength1-1)
    return covariance_matrix_c12

man_c11=man_height_variance
man_c22=man_weight_variance
man_c12=man_c21=get_covariance_matrix_coefficient(man_height,man_weight)
man_covariance_matrix=np.matrix([[man_c11,man_c12],[man_c21,man_c22]])
woman_c11=woman_height_variance
woman_c22=woman_weight_variance
woman_c12=woman_c21=get_covariance_matrix_coefficient(woman_height,woman_weight)
woman_covariance_matrix=np.matrix([[woman_c11,woman_c12],[woman_c21,woman_c22]])

求其决策方程：

# 定义等高线高度函数
def f(sample_height, sample_weight):
    mytemp1=np.zeros(shape=(100,100))
    for i in range(100):
        for j in range(100):
            sample_vector=np.matrix([[sample_height[i,j]],[sample_weight[i,j]]])
            sample_vector_T=np.transpose(sample_vector)
            #定义决策函数
            mytemp1[i,j]=0.5*np.transpose(sample_vector-man_feature_mean_vector)*(np.linalg.inv(man_covariance_matrix))*\
            (sample_vector-man_feature_mean_vector)-0.5*np.transpose(sample_vector-woman_feature_mean_vector)*\
            (np.linalg.inv(woman_covariance_matrix))*(sample_vector-woman_feature_mean_vector)+\
            0.5*math.log((np.linalg.det(man_covariance_matrix))/(np.linalg.det(woman_covariance_matrix)))-\
            math.log(man_priori_probability/woman_priori_probability)
    return mytemp1

使用python库函数plt.contour画类别决策面，并将(160,45)与(178,70)打点与图上，可知(160,45)属于女生，(178,70)属于男生。结果如图二。

完整代码（初版）

import xlrd
import math 
import numpy as np
import scipy.stats as st 
import matplotlib.pyplot as plt
from scipy.stats import norm

'''
/**************************task1**************************/
Take the height as an example, draw a histogram of the 
height of the boys and girls and compare
/**************************task1**************************/
'''
mydata = xlrd.open_workbook('D:/program/py_code/data_2018.xls')
mysheet1 = mydata.sheet_by_name("Sheet1")

#获取行数、列数
nRows=mysheet1.nrows
nCols=mysheet1.ncols

#用于存取男生女生身高数据
man_height=[]
woman_height=[]

#获取第4列的内容:身高
for i in range(nRows):
	if i+1<nRows:
		if mysheet1.cell(i+1,1).value==1:
			man_height.append(mysheet1.cell(i+1,3).value)
		elif mysheet1.cell(i+1,1).value==0:
			woman_height.append(mysheet1.cell(i+1,3).value)

#获取男、女生的数量
manlen=len(man_height)
womanlen=len(woman_height)

#画男女生身高频谱图
plt.hist(man_height,manlen,align='left',color='red',label='boy')
plt.hist(woman_height,womanlen,align='right',label='girl')
plt.legend(loc=0)
plt.xlabel('height')
plt.xlim(min(man_height+woman_height)-1,max(man_height+woman_height)+1)
plt.ylabel('number')
plt.title('Boy height spectrum')
#xsticks与yticks：指定坐标轴的刻度
plt.xticks(np.arange(min(man_height+woman_height),max(man_height+woman_height)+1,1.0))
plt.yticks(np.linspace(0,50,26))
plt.show()

'''
/**************************task2**************************/
Using the maximum likelihood estimation method to find the 
parameters of height and weight distribution for boys and girls
/**************************task2**************************/
'''
#用于存取男生女生体重数据
man_weight=[]
woman_weight=[]

#将男女生体重数据从第5列中进行分离，并保存在上述空数组中
for i in range(nRows):
	if i+1<nRows:
		if mysheet1.cell(i+1,1).value==1:
			man_weight.append(mysheet1.cell(i+1,4).value)
		elif mysheet1.cell(i+1,1).value==0:
			woman_weight.append(mysheet1.cell(i+1,4).value)
#fit(data):Return MLEs for shape, location, and scale parameters from data
#norm.fit(x)就是将x看成是某个norm分布的抽样，求出其最好的拟合参数（mean, std）
man_height_mean, man_height_std 	= norm.fit(man_height)#男生升高分布参数
man_weight_mean, man_weight_std 	= norm.fit(man_weight)#男生体重分布参数
woman_height_mean, woman_height_std = norm.fit(woman_height)#女生升高分布参数
woman_weight_mean, woman_weight_std = norm.fit(woman_weight)#女生体重分布参数

man_height_variance=man_height_std**2
man_weight_variance=man_weight_std**2
woman_height_variance=woman_height_std**2
woman_weight_variance=woman_weight_std**2
print(man_height_mean,man_height_variance,man_weight_mean,man_weight_variance)
print(woman_height_mean,woman_height_variance,woman_weight_mean,woman_weight_variance)

'''
/**************************task3**************************/
采用贝叶斯估计方法，求男女生身高以及体重分布的参数（注明自己选定的参数情况）
/**************************task3**************************/
'''
man_height_mean_cntr, man_height_var_cntr, man_height_std_cntr=st.bayes_mvs(man_height)
man_weight_mean_cntr, man_weight_var_cntr, man_weight_std_cntr=st.bayes_mvs(man_weight)
woman_height_mean_cntr, woman_height_var_cntr, woman_height_std_cntr=st.bayes_mvs(woman_height)
woman_weight_mean_cntr, woman_weight_var_cntr, woman_weight_std_cntr=st.bayes_mvs(woman_weight)
#print(man_height_mean_cntr.statistic,man_weight_mean_cntr.statistic)
#print(woman_height_mean_cntr.statistic,woman_weight_mean_cntr.statistic)

def get_mean_bayes(arr,mean0,variance0,variance):
	datasum=sum(arr)
	datalen=len(arr)
	mean_bayes=(variance0*datasum+variance*mean0)/(datalen*variance0+variance)
	return mean_bayes

'''
特殊情况1:
variance0=0时，mean_bayes=mean0
先验知识可靠，样本不起作用
#以男生身高为例，选定参数：mean0=20,variance=10,variance0=0
'''
man_height_mean_bayes=get_mean_bayes(man_height,20,0,10)
print(man_height_mean_bayes)

'''
特殊情况2:
variance0>>variance时，mean_bayes=sample_mean
先验知识十分不确定，完全依靠样本信息,结果与最大似然估计结果近似
#以女生身高为例，选定参数：mean0=50,variance=1,variance0=100
'''
woman_height_mean_bayes=get_mean_bayes(woman_height,50,100,1)
print(woman_height_mean_bayes)

'''
/**************************task4**************************/
4.	采用最小错误率贝叶斯决策，画出类别判定的决策面。并判断某样本
的身高体重分别为(160,45)时应该属于男生还是女生？为(178,70)时呢？
/**************************task4**************************/
'''
#①本题输入类数为2：即男生、女生；特征数为2：即身高、体重
#②求协方差矩阵
def get_covariance_matrix_coefficient(arr1,arr2):#arr1与arr2长度相等
	datalength1=len(arr1)
	datalength2=len(arr2)
	sum_temp=[]
	for i in range(datalength1):
		sum_temp.append((arr1[i]-sum(arr1)/datalength1)*(arr2[i]-sum(arr2)/datalength2))
		c12=sum(sum_temp)
	covariance_matrix_c12=c12/(datalength1-1)
	return covariance_matrix_c12

man_c11=man_height_variance
man_c22=man_weight_variance
man_c12=man_c21=get_covariance_matrix_coefficient(man_height,man_weight)
man_covariance_matrix=np.matrix([[man_c11,man_c12],[man_c21,man_c22]])
woman_c11=woman_height_variance
woman_c22=woman_weight_variance
woman_c12=woman_c21=get_covariance_matrix_coefficient(woman_height,woman_weight)
woman_covariance_matrix=np.matrix([[woman_c11,woman_c12],[woman_c21,woman_c22]])
print(woman_covariance_matrix)

#求男生、女生先验概率
man_priori_probability=manlen/(manlen+womanlen)
woman_priori_probability=1-man_priori_probability
#print(woman_priori_probability)

man_feature_mean_vector=np.matrix([[man_height_mean],[man_weight_mean]])
woman_feature_mean_vector=np.matrix([[woman_height_mean],[woman_weight_mean]])

# 定义等高线高度函数
def f(sample_height, sample_weight):
    mytemp1=np.zeros(shape=(100,100))
    for i in range(100):
    	for j in range(100):
            sample_vector=np.matrix([[sample_height[i,j]],[sample_weight[i,j]]])
            sample_vector_T=np.transpose(sample_vector)
            #定义决策函数
            mytemp1[i,j]=0.5*np.transpose(sample_vector-man_feature_mean_vector)*(np.linalg.inv(man_covariance_matrix))*\
            (sample_vector-man_feature_mean_vector)-0.5*np.transpose(sample_vector-woman_feature_mean_vector)*\
            (np.linalg.inv(woman_covariance_matrix))*(sample_vector-woman_feature_mean_vector)+\
            0.5*math.log((np.linalg.det(man_covariance_matrix))/(np.linalg.det(woman_covariance_matrix)))-\
            math.log(man_priori_probability/woman_priori_probability)
    return mytemp1

sample_height = np.linspace(150, 180, 100)
sample_weight = np.linspace(40, 80, 100)
# 将原始数据变成网格数据
Sample_height, Sample_weight = np.meshgrid(sample_height, sample_weight)
# 填充颜色
plt.contourf(Sample_height, Sample_weight, f(Sample_height,Sample_weight), 0, alpha = 0)
# 绘制等高线,圈内为女生，圈外为男生
C = plt.contour(Sample_height, Sample_weight, f(Sample_height,Sample_weight), 0, colors = 'black',linewidths=0.6)
# 显示各等高线的数据标签
plt.clabel(C, inline = True, fontsize = 10)

#显示男女生样本散点图

p1=plt.scatter(man_height, man_weight,c='g', marker = '*',linewidths=0.4)
p2=plt.scatter(woman_height, woman_weight,c='r', marker = '*',linewidths=0.4)


# 定义显示坐标函数
def Display_coordinates(m, n):
	plt.scatter(m, n, marker = 's',linewidths=0.4)
	plt.annotate((m,n), xy = (m, n))
	return

#并判断某样本的身高体重分别为(160,45)时应该属于男生还是女生？为(178,70)时呢
Display_coordinates(160,45)
Display_coordinates(178,70)
label=['boy','girl']
plt.legend([p1, p2],label,loc=0)
plt.xlabel('height/cm')
plt.ylabel('weight/kg')
plt.show()

本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容，请联系:hwhale#tublm.com(使用前将#替换为@)

模式识别

最小错误率贝叶斯决策分类