FFT，即为快速傅氏变换，是离散傅氏变换的快速算法，它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。它对傅氏变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。这是360百科中对于fft的一种概念解释。我们可以这么理解：FFT（Fast Fourier Transformation）就是“快速傅里叶变换”的意思，它是一种用来计算DFT（离散傅里叶变换）和IDFT（离散傅里叶反变换）的一种快速算法。这种算法运用了一种高深的数学方式、把原来复杂度为O(n2)的朴素多项式乘法转化为了O(nlogn)的算法。
那么这种快速傅里叶变换是如何实现的呢？由于离散信号是由很多点组成的，所以DFT的公式如公式1所示。而连续信号的傅里叶变换是在连续域中进行的运算，其积分运算公式如公式2所示。离散傅里叶变换将这个积分运算变为了累加运算，即使如此，实际运算量也依然非常可观。所以在实际的应用场景中，离散傅里叶变换的实用性较差。因此，FFT作为新的计算方式被广泛接受。其本质是将离散傅里叶变换通过它本身的奇、偶、虚、实的性质，对该公式进行推导改进。公式1中的k和t均为时域中的输入参数，X(k)以及F[f(t)]即为相对与x以及t的傅里叶变换。
公式1
公式2
首先我们对于离散傅里叶变换的公式进行转换推导。离散傅里叶变换实际可以表示为：
公式3
我们改变一种表示方式，离散傅里叶变换也可以表示为
公式4
对于这种公式，我们应该如何来进行求解呢。在这里我们不进行传统计算方式的介绍，直接按照fft的思想来进行解析推导。
首先，我们对于多项式进行分解，现在我们将该多项式分解为奇数次项和偶数次项的进行分类表示。而且为了表现的更清楚，我们先将该多项式的最高次项定为7，即有8个多项式进行累加，然后重新排列后的多项式为：
公式5
为了表示的更清晰，我们分别给奇数次项和偶数次项重新起一个名字，即f(x)和g(x)，这两个多项式依次表示为：
公式6
公式7
对该公式进行还原，我们又可以还原回原来的总公式。
公式8
之前我们的思维一直停留在实数范畴内，现在我们引入一个复数域内的概念。我们叫它复根用ω 表示。如果=1 ，那么我们称“ω 为1的k次复根”计做
，单位复根地表示，其中n就是一个序号数，我们把所有的负根按照复数域角度的大小逆时针排序从零开始编号。
如下图所示，即为一个四次复根的图形表示。
图 1 四次复根
根据该图我们可以推论，其实k次复根就相当于是将图中的圆周平均分成k个弧，弧与弧之间的端点就是k次复根。另外，从图中可以看出 = -1 =
=
，
是这个圆与“Real”轴即实数轴正半轴的交点，所以无论k取多少，
始终是1。我们只需要知道
，就能求出
，所以我们称
为“单位复根”。
在正常使用过程中，我们也能够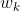表示单位复根，
表示的是“单位复根”的“1次方”也就是它本身,其他的就叫做k次单位复根的n次方。
关于单位复根，它还有一些特性，
现在我们将单位复根带入上述的公式中代替x的值，则原来的公式可以表示为:
公式9
由于需要对n进行分类讨论，因为涉及到奇偶次项的运算，当0 <n <k/2 -1时 ，此时根据之前提到的复根的折半引理，我们可以将该公式推导为：
公式10
当k/2<n +k/2<k -1时,上述的公式又可以变为
公式11
根据之前的消去定理以及折半定理，我们可以将公式优化为：
公式12
所以，fft的计算公式可以总结为两个区域内的值表示，即0 <n <k/2 -1以及k/2<n +k/2<k -1的区间范围内所有Fx 的值都可以表示，另外，可以看出fx 以及 gx 就是 Fx 的一半，因此在程序计算过程中可以按照子问题的方式来递归求解。
以下即为根据上述推导处的最后两个公式来进行计算的fft代码表示。代码中涉及到的子函数均为复数间的计算。
void fft(complex *a,int n,int dft)//n表示我的多项位数
{
int i = 0, j = 0, k = 0;
int step = 0;
for(i=0;i<n;i++) if(i<rev[i]) Swap(a[i],a[rev[i]]);
for(step=1;step<n;step<<=1)//模拟一个合并的过程
{
complex wn;
Wn_i(n,1,&wn,dft);//计算当前单位复根
for(j=0;j<n;j+=step<<1)
{
complex wnk;
Wn_i(n,1,&wnk,dft);//计算当前单位复根
for(k=j;k<j+step;k++)
{//蝴蝶操作
complex x=a[k];
complex y;
c_mul(a[k+step],wnk,&y);
c_plus(x,y,&a[k]);
c_sub(x,y,&a[k+step]);//后半个“step”中的ω一定和“前半个”中的成相反数
c_mul(wnk,wn,&wnk);
}
}
}
}
为了得到蝶形计算的参数序号，在进行fft计算之前先要进行参数重新排序，该函数的目的就是将每一位颠倒。如果暴力按位反转，总归不够优雅。所以，我们用一个类似DP动态规划的方法来实现这个功能。代码如下所示：
void get_rev(int bit)//bit表示二进制的位数
{
for(int i=0;i<(1<<bit);i++)//我么要对1~2^bit-1中的所有数做长度为bit的二进制翻转
rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));//?!! SMG ?!!
}
根据dp的思想，每一个问题都可以由其子问题的解来进行求解。所以我们可以把一个二进制数看成两部分，它的前bit-1位是一部分，它的最后一位是一部分。全部bit位的数据求解看成是总问题，则前bit-1位可以看成是一个子问题。所以，要求解所有位数据的反转，我们可以直接利用前bit-1位数据的反转结果。因此，任意一个数的二进制反转就相当于是把它的最后一位当成首位，然后在后面接上它前bit-1位的二进制反转。而且在这个循环中我们能保证，在计算i的二进制反转之前，1 ~ i-1中的所有数的二进制反转都已经完成。 i的前bit-1位的数值其实就是i >>1的值，直接调用 i >>1的二进制反转的结果就相当于调用了i 的前bit-1位二进制反转的结果。
其实i >>1的反转与i的前bit-1位的反转是有一点出入的，因为我们的二进制反转始终以bit位为标准，所以i >>1会比i的前bit-1位多出一个前导零，而反转之后就会多出一个后缀零，所以i的前bit-1位的反转要去掉那个后缀零，此处我们通过将结果向右移位来实现，也就是rev[i>>1]>>1。
因此，我们只要把末尾乘上2^(bit-1)变成首位，此时该数据除了最高位有效之外，其余所有数位全都是向左移位产生的0，所以，再按位或（|）上rev[ i >>1]>>1就是我们要的答案了。
关于快速傅里叶变换，我的学习过程属于比较坎坷的一类，大学期间曾经学习过一段时间，但那时对于这些概念没有深入的学习，所以压根没有理解。即使后来再次遇到这些概念及公式也是一头雾水。现在由于工作过程中需要用到这些知识，所以便重新回来翻看。快速傅里叶变换作为工程上的一种工具，通过很巧妙的手段将公式重组简化，大大提高了多项式乘法以及离散傅里叶变换的计算速度。学习期间上网查阅过很多前辈总结的学习笔记，在此向各位提供学习心得的前辈表示衷心的感谢！
参考文献
https://blog.csdn.net/WADuan2/article/details/79529900
https://blog.csdn.net/tf18269639242/article/details/53024276
https://blog.csdn.net/f_zyj/article/details/76037583
https://wenku.baidu.com/view/5cacb2b8bd64783e09122b9a.html
https://blog.csdn.net/chenyujing1234/article/details/7419863
https://www.cnblogs.com/luoqingyu/p/5930181.html
https://blog.csdn.net/ggn_2015/article/details/68922404
https://blog.csdn.net/egean/article/details/53039248
https://blog.csdn.net/ggn_2015/article/details/68922404
https://blog.csdn.net/linwanglian1/article/details/56020221
https://www.cnblogs.com/RabbitHu/p/FFT.html
https://www.cnblogs.com/Lyush/articles/3219196.html
https://blog.csdn.net/zhaopeizhaopeipei/article/details/53908238
https://blog.csdn.net/shenziheng1/article/details/52891807