一、概述
数据流分析是用于编译时程序分析的经典技术,它使编译器能够推断程序中的值在运行时的流动。
在简单的情况下,静态分析可以生成精确的结果,此时编译器能够确切地知道在代码执行时到底将发生什么。如果编译器能够推导出精确信息,那么它可以将表达式或函数的运行时求值操作替换为对(编译时预计算)结果的立即数加载操作。另一方面,如果代码从任何外部来源读取值、涉及(即使很少的)控制流,或者遇到具有歧义的内存引用(指针、数组引用或引用调用参数),那么静态分析会变得困难得多,而分析的结果也会变得不那么精确。
二、迭代数据流分析
编译器使用数据流分析来确定可进行优化的机会,并证明特定变换的安全性。如优化简介中利用活跃信息查找未初始化变量所见,数据流分析方面的问题呈现为一组联立方程的形式,方程定义在与某个图的结点和边相关联的集合上,而该图表示了被分析的代码。活跃信息分析即表述为过程控制流图上的一个全局数据流问题。
2.1 支配性
在入口结点为b0的流图中,当且仅当bi位于从b0到bj的每条路径上时,结点bi支配结点bj,也可以说结点bi是结点bj的支配者。
集合Dom(bj)包含了支配bj的所有结点的名字。如下图CFG中的结点B6,从B0到B6的每条代码路径都包含了结点B0、B1、B5和B6,因此Dom(B6)为{B0,B1,B5,B6}。
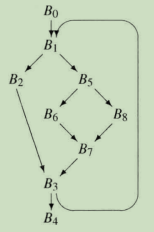
该CFG所有结点对应的Dom集合如下列出:

编译器可以通过以下支配性方程来计算这些集合 :
D
o
m
(
n
)
=
{
n
}
∪
(
⋂
m
∈
p
r
e
d
s
(
n
)
D
o
m
(
m
)
)
Dom(n) = \{ n \} \cup \big( \bigcap_{m \isin preds(n)} Dom(m) \big)
Dom(n)={n}∪(⋂m∈preds(n)Dom(m))
其中
p
r
e
d
s
(
n
)
preds(n)
preds(n)表示n的前驱结点集合,方程的初始条件为:
D
o
m
(
n
0
)
=
n
0
Dom(n_0) = {n_0}
Dom(n0)=n0,且
∀
n
≠
n
0
\forall n \ne n_0
∀n=n0,
D
o
m
(
n
)
=
N
Dom(n)=N
Dom(n)=N,N是CFG的所有结点集合。
下图9-1是支配性方程的一个循环迭代求解算法。该算法按照结点在CFG中名字的顺序依次处理各个结点,即B0、B1、B2等。算法会初始化各个结点的Dom集合,然后反复地重算这些Dom集合,直至集合内容不再发生变化为止。就我们的例子而言,算法生成的Dom集合包含下表中的值。
第一列给出了迭代编号,横线标记的行给出了各个Dom集合的初始值。在第一次迭代中,算法对于从B0出发只有单一路径可达的结点直接计算出了正确的Dom集合,但对B3、B4和B7算出的Dom集合过大。在第二次迭代中,计算得到的Dom(B7)集合较小,该集合进而校正了Dom(B3),后者又使得Dom(B4)集合变小。类似地,Dom(B8)也会校正Dom(B7)。此时,还需要进行第三次迭代,才能确认算法已经到达了一个不动点。

2.2 活跃变量分析
活跃变量分析在学习《利用活跃信息查找未初始化变量》时已经对其做了详细总结,这里只是提一下。
活跃变量的定义:对于变量x和程序点p,如果在CFG中沿着p开始能找到一条或多条会引用变量x在p点的值的路径,且变量x在该路径中没有被重新定义时,则称变量x在点p是活跃(live)的,否则称变量x在点p不活跃(dead)。
我们通过计算,将过程中每个基本程序块b对应的活跃信息编码到集合
L
i
v
e
O
u
t
(
b
)
LiveOut(b)
LiveOut(b)中,该集合包含在从程序块b退出时所有活跃的变量。
对于过程的CFG中每个结点n来说,定义LiveOut集合的方程如下:
L
i
v
e
O
u
t
(
n
)
=
⋃
m
∈
s
u
c
c
(
n
)
(
U
E
V
a
r
(
m
)
∪
(
L
i
v
e
O
u
t
(
m
)
∩
V
a
r
K
i
l
l
(
m
)
‾
)
)
LiveOut(n)= \bigcup_{m \isin succ(n)} (UEVar(m) \cup (LiveOut(m) \cap \overline{VarKill(m)}))
LiveOut(n)=⋃m∈succ(n)(UEVar(m)∪(LiveOut(m)∩VarKill(m)))
其中
s
u
c
c
(
n
)
succ(n)
succ(n)表示结点
n
n
n的所有后继结点,方程的初始条件是:
∀
n
\forall n
∀n,使得
L
i
v
e
O
u
t
(
n
)
=
∅
LiveOut(n) = \emptyset
LiveOut(n)=∅ 。
LiveOut方程与Dom方程对比:比较约束LiveOut和Dom的方程式可以揭示间题之间的差别。LiveOut是一个反向数据流问题,因为LiveOut(n)是作为n在CFG中各个后继结点入口处已知信息的函数来计算的。Dom是一个正向数据流问题,因为Dom(n)是作为n在CFG中各个前趋结点出口处巳知信息的函数来计算的。LiveOut寻找的是CFG中任何路径上未来可能的使用之处,因而它会使用并集运算符合并来自多条路径的信息。Dom寻找的是在进入入口结点的所有路径上都存在的前趋结点,因而它使用交集运算符合并来自多条路径的信息。最后,LiveOut会推断代码中各个操作的效应。为此,它使用特定于程序块的常量集合UEVar和VarKill,这两种集合是从各个程序块的代码推导而来的。与此相反,Dom只处理CFG的结构。于是,其特定于程序块的常量集合只包含程序块的名字。
再带入一个新的例子到《解决这个数据流问题》的算法中,下图9-2a给出了各个基本程序块的代码,9-2b给出了CFG,9-2c给出了各个程序块的UEVar和VarKill集合。
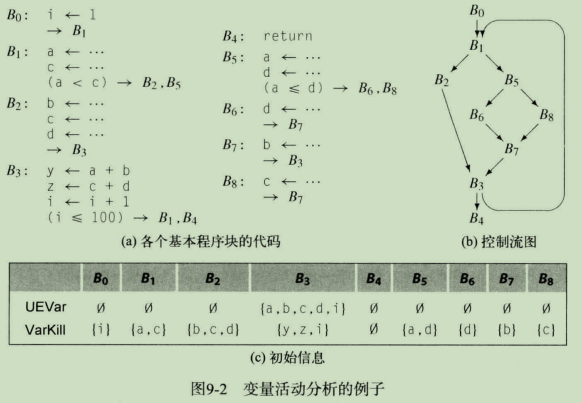
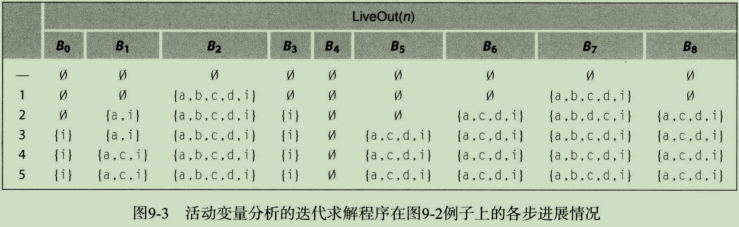
下图9-3给出了迭代求解程序在上图9-2所示例子上求解的各步进展情况,其中使用的RPO次序与我们在Dom计算中使用的相同,即B0、B1、B5、B8、B6、B7、B2、B3、B4。尽管约束LiveOut的方程比Dom的更为复杂,但其控制可停止性、正确性和效率的参数却与支配性方程颇为相似。
2.3 数据流分析的局限性
数据流分析的局限性主要体现在两个方面。
一种是在对CFG中的结点n计算LiveOut集合时,迭代算法需要使用n在CFG中所有后继结点的LiveOut、UEVar和VarKill集合。这隐含地假定执行可以到达所有这些后继结点,实际上其中一个或多个结点可能不是可到达的。下图实例中,数据流分析和程序实际执行路径可能会不同。
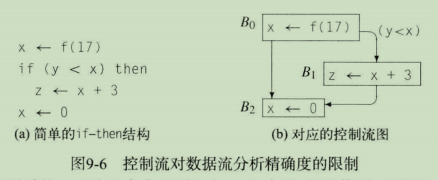
B0中对x的赋值是活跃的,因为B1会用到这个x。B2中对x的赋值则“杀死”了B0中设置的x值。如果B1不能执行,那么在执行过x与y的比较指令后,B0中x的值将变得不再活跃,因而x
∉
\notin
∈/ LiveOut(B0)。如果编译器可以证明(y<x)这个条件判断的结果总为false,那么控制从来不会转入到程序块B1中,因而对z的赋值也从不会执行。如果对f的调用没有副效应,那么B0中的整条语句都是无用的,没有必要执行。由于条件判断的结果是已知的,编译器可以完全删除程序块B0和B1。
但是,约束LiveOut的方程会对程序块所有后继结点(而不只是可执行后继结点)的贡献取并集,活跃变量分析程序计算的方程结果为:
L
i
v
e
O
u
t
(
B
0
)
=
U
E
V
a
r
(
B
1
)
∪
L
i
v
e
O
u
t
(
B
1
)
∩
V
a
r
K
i
l
l
(
B
1
)
‾
∪
U
E
V
a
r
(
B
2
)
∪
L
i
v
e
O
u
t
(
B
2
)
∩
V
a
r
K
i
l
l
(
B
2
)
‾
LiveOut(B_0)= UEVar(B_1) \cup LiveOut(B_1) \cap \overline{VarKill(B_1)} \cup UEVar(B_2) \cup LiveOut(B_2) \cap \overline{VarKill(B_2)}
LiveOut(B0)=UEVar(B1)∪LiveOut(B1)∩VarKill(B1)∪UEVar(B2)∪LiveOut(B2)∩VarKill(B2)
另一种在数据流分析结果中悄然产生不精确性的途径,来自于对数组、指针和过程调用的处理。数组引用,如A[i,j,k],引用的是A中的一个元素。然而,如果分析无法揭示i、j、k的值 ,则编译器无法断定正在访问A中的哪个元素。为此,编译器传统上将对数组元素的引用都归为对整个数组A的引用,所以对A[x,y,z]的一次使用将算作是对A的一次使用,对A[c,d,e]的一次定义将算作是对A的一次定义。
2.4 其他数据流问题
2.4.1 可用表达式
直观意义:在点p上,x op y已经在之前被计算过,不需要重新计算,x op y被称为可用表达式。
定义:当且仅当在从某过程的入口点到p处的每条代码路径上e都已经求值,且从求值处到p之间e的任何子表达式都没有重新定义时,表达式e在该过程中位置p处是可用的。
对CFG中的每个结点n,用一个集合AvailIn(n)来表示,过程中从程序入口处到结点n的所有可用表达式的名字。定义AvailIn(n)集合的方程如下:
A
v
a
i
l
I
n
(
n
)
=
⋂
m
∈
p
r
e
d
s
(
n
)
(
D
E
E
x
p
r
(
m
)
∪
(
A
v
a
i
l
I
n
(
m
)
∩
E
x
p
r
K
i
l
l
(
m
)
‾
)
)
AvailIn(n)= \bigcap_{m \isin preds(n)} (DEExpr(m) \cup (AvailIn(m) \cap \overline{ExprKill(m)}))
AvailIn(n)=⋂m∈preds(n)(DEExpr(m)∪(AvailIn(m)∩ExprKill(m)))
方程的初始条件为:
A
v
a
i
l
I
n
(
n
0
)
=
∅
AvailIn(n_0) = \emptyset
AvailIn(n0)=∅,
A
v
a
i
l
I
n
(
i
)
=
{
a
l
l
AvailIn(i)= \{ all
AvailIn(i)={all
e
x
p
r
e
s
s
i
o
n
}
expression \}
expression},
∀
n
≠
n
0
\forall n \ne n_0
∀n=n0
其中:
-
p
r
e
d
s
(
n
)
preds(n)
preds(n)表示n的所有前驱结点。
-
D
E
E
x
p
r
(
n
)
DEExpr(n)
DEExpr(n)是n中向下展示的表达式的集合。表达式
e
∈
D
E
E
x
p
r
(
n
)
e \isin DEExpr(n)
e∈DEExpr(n),当且仅当:程序块n对表达式e进行了求值,且在n中对e的最后一次求值的位置到程序块n末尾之间,e的操作数都没有被定义过。
-
E
x
p
r
K
i
l
l
(
m
)
ExprKill(m)
ExprKill(m)是m中定义的表达式集合,即被程序块m中的定义“杀死”的所有表达式。
表达式e在程序块n入口处是可用的,当且仅当:在CFG中n的每个前趋结点出口处,该表达式都是可用的。按方程的描述,欲使表达式e在某个程序块m出口处是可用的,需满足两个条件之一:e在m中是向下展示的,或者它在m的入口处就是可用的且在m中没有被“杀死”。
AvailIn集合可用于进行全局冗余消除(global redundancy elimination),有时也称为全局公共子表达式消除(global common subexpression elirnination)。或许实现这种效果最简单的方法是对每个基本程序块计算AvailIn集合,然后在局部值编号算法中使用这些集合,编译器在对程序块b进行值编号之前,只需将程序块b的散列表初始化为AvailIn(b)。缓式代码移动(lazy code motion)是一种更强形式的公共子表达式消除,它也利用了表达式的可用性(后续会讲)。
2.4.2 可达定义
有时候,编译器需要知道操作数是在何处定义的。如果在CFG中有多条代码路径通向该操作,那么可能有多个定义提供了该操作数的值。为找到能够到达某个基本程序块的定义的集合,编译器可以计算可达定义。Reaches的域是所述过程中定义的集合。某个变量v的一个定义d能够到达操作i,当且仅当:i读取v的值,存在一条从d到i的代码路径,且该路径没有再次定义v。
下面代码中,L1中对v的定义d1,L2中对v的定义d2。当删掉定义d2,v的定义d1对操作i = v + 1来说是可达的;不删掉定义d2,定义d1对操作i = v + 1来说是不可达的,而定义d2是可达的。
L1:
v = 123 // d1
br L2
L2:
v = 456 // d2
i = v + 1
编译器将可达定义作为一个正向数据流问题计算,最终将CFG中的每个结点n用集合Reaches(n)标注,方程如下:
R
e
a
c
h
e
s
(
n
)
=
⋃
m
∈
p
r
e
d
s
(
n
)
(
D
E
D
e
f
(
m
)
∪
(
R
e
a
c
h
e
s
(
m
)
∩
D
e
f
K
i
l
l
(
m
)
‾
)
)
Reaches(n)= \bigcup_{m \isin preds(n)} (DEDef(m) \cup (Reaches(m) \cap \overline{DefKill(m)}))
Reaches(n)=⋃m∈preds(n)(DEDef(m)∪(Reaches(m)∩DefKill(m)))
方程的初始条件为:
R
e
a
c
h
e
s
(
n
)
=
∅
Reaches(n) = \emptyset
Reaches(n)=∅,
∀
n
\forall n
∀n
其中:
-
p
r
e
d
s
(
n
)
preds(n)
preds(n)表示n的所有前驱结点。
-
D
E
D
e
f
(
m
)
DEDef(m)
DEDef(m)集合包含了m中所有向下展示的定义:程序块m中的定义,且已定义的名字在m内未被后续指令重新定义。
-
D
e
f
K
i
l
l
(
m
)
DefKill(m)
DefKill(m)集合包含了被m中同名定义掩盖的所有定义位置;如果d定义了某个名字v,而m包含了一个定义v的定义,那么
d
∈
D
e
f
K
i
l
l
(
m
)
d \isin DefKill(m)
d∈DefKill(m)。因而
D
e
f
K
i
l
l
(
m
)
‾
\overline{DefKill(m)}
DefKill(m)包含了m中可见的所有定义位置。
DEDef和DefKill都定义在定义位置的集合之上,但计算二者都需要从名字(变量和编译器产生的临时变量的名字)到定义位置的映射。因而,对可达定义问题收集初始信息比处理活跃变量问题更为复杂。
可达定义也被叫做到达-定值,其主要用途:
- 循环不变计算的检测:如果循环中含有赋值
x=y+z ,而y和z所有可能的定值都在循环外面(包括y或z是常数的特殊情况) ,那么y+z就是循环不变计算。
- 常量合并:如果对变量x的某次使用只有一个定值可以到达,并且该定值把一个常量赋给x,那么可以简单地把x替换为该常量
- 判定变量x在p点上是否未经定值就被引用
如果觉得这块内容理解困难,可参考《数据流分析:定义可达分析(reaching definition analysis)》中对可达定义的解释。不过我没有读这篇文章,不知道写的咋样,反正看着挺详细的。
2.4.3 可预测表达式
表达式e在程序块b的出口处被认为是可预测的(或非常繁忙),当且仅当:(1)每条离开b的代码路径都对e进行求值并后续使用它;且(2)在b的末尾处对e进行求值,所得结果与沿任一路径回溯到e第一次求值的结果都是相同的。术语“可预测的“得名于第二个条件,该条件意味着:e在b中的一次求值可用于预测其沿所有代码路径的任一后续求值结果。程序块退出时可预测的表达式集合,可以作为CFG上的一个反向数据流问题进行计算。该问题的域是表达式的集合,定义AntOut(n)集合的方程如下:
A
n
t
O
u
t
(
n
)
=
⋂
m
∈
s
u
c
c
(
n
)
(
U
E
E
x
p
r
(
m
)
∪
(
A
n
t
O
u
t
(
m
)
∩
E
x
p
r
K
i
l
l
(
m
)
‾
)
)
AntOut(n)= \bigcap_{m \isin succ(n)} (UEExpr(m) \cup (AntOut(m) \cap \overline{ExprKill(m)}))
AntOut(n)=⋂m∈succ(n)(UEExpr(m)∪(AntOut(m)∩ExprKill(m)))
方程的初始条件为:
A
n
t
O
u
t
(
n
f
)
=
∅
AntOut(n_f) = \emptyset
AntOut(nf)=∅,
A
n
t
O
u
t
(
n
)
=
{
a
l
l
AntOut(n)= \{ all
AntOut(n)={all
e
x
p
r
e
s
s
i
o
n
}
expression \}
expression},
∀
n
≠
n
f
\forall n \ne n_f
∀n=nf
其中:
-
s
u
c
c
(
n
)
succ(n)
succ(n)表示结点
n
n
n的所有后继结点。
-
U
E
E
x
p
r
(
n
)
UEExpr(n)
UEExpr(n)是n中向上展示的表达式的集合,即那些在被“杀死”之前会在m中用到的表达式。
-
E
x
p
r
K
i
l
l
(
m
)
ExprKill(m)
ExprKill(m)是m中定义的表达式集合,即被程序块m中的定义“杀死”的所有表达式。
可预测性分析的结果会用到代码移动中,目的有二:一是减少执行时间,如用于缓式代码移动;二是减小编译后代码的长度,如用于代码提升(code hoisting)。
2.4.4 过程间综述问题
单个过程调用,被调过程可能会修改它和调用过程都能访问到的所有变量(全局变量、模块级变量和引用调用参数),所以编译器要计算过程间可能会修改的变量集合。
编译器有一些方式可以计算出襄括某个调用位置所有副效应的集合。将被调用者及其调用的过程可能修改的变量名的集合计算出来,标注到每个对应的调用位置上。”可能修改”问题是程序调用图上的一组数据流方程,意在为每个过程标注一个MayMod集合。
M
a
y
M
o
d
(
p
)
=
L
o
c
a
l
M
o
d
(
p
)
∪
(
⋃
e
=
(
p
,
q
)
u
n
b
i
n
d
e
(
M
a
y
M
o
d
(
q
)
)
)
MayMod(p) = LocalMod(p) \cup \Big( \bigcup_{e = (p, q)} unbind_e (MayMod(q)) \Big)
MayMod(p)=LocalMod(p)∪(⋃e=(p,q)unbinde(MayMod(q)))
其中e = (p,q)是调用图中从p到q的一条边。函数
u
n
b
i
n
d
e
unbind_e
unbinde,将一个变量名集合映射到另一个。对于调用图中的一条边e = (p,q)而言,
u
n
b
i
n
d
e
(
x
)
unbind_e(x)
unbinde(x)(使用对应于e的具体调用位置处的绑定关系,将x中的每个名字从q的名字空间映射到p的名字空间。最后,
L
o
c
a
l
M
o
d
(
p
)
LocalMod(p)
LocalMod(p)集合包含了在p本地修改过且在p外部可见的所有名字。计算该集合时,将p中所有定义过的名字的集合减去只属于p局部作用域的名字即可。
为求解MayMod,编译器可以将所有过程p的
M
a
y
M
o
d
(
p
)
MayMod(p)
MayMod(p)都初始化为
L
o
c
a
l
M
o
d
(
p
)
LocalMod(p)
LocalMod(p),然后对方程进行迭代求值,直至到达一个不动点。给出每个过程的MayMod集合,编译器通过计算集合
S
=
u
n
b
i
n
d
e
(
M
a
y
M
o
d
(
q
)
)
S=unbind_e(MayMod(q))
S=unbinde(MayMod(q)),然后将p中那些与S中某些名字互为别名的名字都添加到S中,就可以计算任一具体调用e=(p,q)处可能修改的名字的集合。
三、静态单赋值形式
随着时间的推移,许多不同的数据流问题已经得以阐明。如果每种变换都使用其自身特异性的分析,那么在分析这一趟处理上花费的实现、调试及维护方面的时间和工作可能变得过多。为限制编译器编写者必须实现和编译器必须运行的分析的数目,使用单趟分析来支持多种变换是可取的。
实现此类“通用“分析的一种策略涉及建立程序的一种变体形式,将数据流和控制流均直接编码到IR中,而静态单赋值形式的IR具有这种性质。静态单赋值形式的代码满足两种约束规则:
- 每个定义都产生唯一的名字。
- 每次使用都引用单一的定义。
3.1 构造静态单赋值形式的简单方法
为构造程序的静态单赋值形式,编译器必须向CFG中的汇合点处插入
ϕ
\phi
ϕ函数,且必须重命名变量和临时值,使之符合支配静态单赋值形式名字空间的规则。该算法概述如下:
-
插入
ϕ
\phi
ϕ函数。在具有多个前趋的每个程序块起始处,为当前过程中定义或使用的每个名字y,插入一个
ϕ
\phi
ϕ函数,如y
←
ϕ
\gets \phi
←ϕ(y,y)。对于CFG中的每一个前趋块,
ϕ
\phi
ϕ函数都应该有一个参数与之对应。这一规则在需要插入
ϕ
\phi
ϕ函数之处均插入一个
ϕ
\phi
ϕ函数。当然它也插入了许多非必要的
ϕ
\phi
ϕ函数。
-
重命名。在插入
ϕ
\phi
ϕ函数之后,编译器可以计算可达定义(2.4.2节)。由于插入的
ϕ
\phi
ϕ函数也是定义,它们确保了对任一使用处都只有一个定义能够到达。接下来,编译器可以重命名每个使用处的变量和临时值,以反映到达该处的定义。
该算法为程序构造出了一个正确的静态单赋值形式,称为最大SSA(maximal SSA),但该算法产生的静态单赋值形式可能具有很多不必要的
ϕ
\phi
ϕ函数,它们会降低在静态单赋值形式上执行的某些种类分析的精确度。它们会占用空间,使得编译器浪费内存来表示冗余等。
3.2 支配边界
上面构造静态单赋值形式的简单方法会产生很多不必要的
ϕ
\phi
ϕ函数,解决这个问题,须理解在每个汇合点处,具体哪个变量需要
ϕ
\phi
ϕ函数。
支配性前面已经解释过,这里又整出个新活,严格支配性。当且仅当a
∈
\isin
∈ DOM(b) - {b}时,a严格支配b;a不严格支配b则是,当且仅当a
∉
\notin
∈/ DOM(b) - {b},变相推出a = b 或 a
∉
\notin
∈/ DOM(b)时成立。
考虑CFG的结点n中的一个定义。该值到达某个结点m时,如果n
∈
\isin
∈ Dom(m),则该值不需要
ϕ
\phi
ϕ函数,因为到达m的每条代码路径都必然经由n。该值无法到达m的唯一可能是有另一个同名定义的干扰,即在n和m之间的某个结点p中,出现了与该值同名的另一个定义。在这种情况下,在n中的定义无需
ϕ
\phi
ϕ函数,而p中的重新定义则需要。
结点n中的定义,仅在CFG中n支配区域以外的汇合点,才需要插入相应的
ϕ
\phi
ϕ函数。更具体的说,结点n中的定义,仅在满足下述两个条件的汇合点处才插入对应的
ϕ
\phi
ϕ函数:
- n支配m的一个前趋(m是一个汇合点),即q
∈
\isin
∈ preds(m)且n
∈
\isin
∈ Dom(q)。
- n并不严格支配m,即n = m 或 n
∉
\notin
∈/ DOM(m)。使用严格支配性而非支配性,可以使得在单个基本程序块构成的循环起始处插入一个
ϕ
\phi
ϕ函数(在这种情况下,n = m)。
同时满足以上两个条件的结点m的集合,称为n的支配边界,记作DF(n)。更直观的解释,如果n支配m的一个前驱结点,但是n不直接支配m(或者n = m),则m就是n的支配边界,DF(n) = m。
DF(n)包含:在离开n的每条CFG路径上,从结点n可达但不支配的第一个结点。在 2.1 支配性 的CFG中,B5支配B6、B7和B8,但并不支配B3。在每条离开B5的路径上,B3都是B5不支配的第一个结点,因而,DF(B5)={B3}。
1) 支配者树
上文 2.1 支配性 中的CFG例子对应的支配者树如下图。给出流图中的一个结点n,严格支配n的结点集是Dom(n) - {n}。该集合中与n最接近的结点称为n的直接支配结点,记作IDom(n)。流图的入口结点没有直接支配结点。
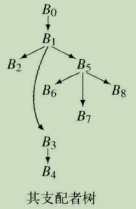
如果m为IDom(n),那么支配者树中有一条边从m指向n。给出支配者树中的一个结点n,IDom(n)只是其在树中的父结点。Dom(n)中的各个结点,就是从支配者树的根结点到n之间的路径上的那些结点(含根结点和n)。从支配者树中,可以读取Dom(n)和IDom(n)集合,如下图。

2) 计算支配边界
为高效地插入
ϕ
\phi
ϕ函数,我们需要为流图中的每个结点计算支配边界。使用支配者树和CFG,我们可以表示出一个简单且直接的计算支配边界算法,如下图所示。该算法基于三个见解:
- 第一,DF集合中的结点必定是图中的汇合点,因为CFG中只有汇合点才是支配边界的成员。
- 第二,对于一个汇合点
j
j
j,
j
j
j的每个前趋结点k必定有
j
∈
D
F
(
k
)
j\isin DF(k)
j∈DF(k),因为如果
j
j
j具有多个前趋结点,则k是无法支配的。
- 第三,如果对
j
j
j的某些前趋结点k,
j
∈
D
F
(
k
)
j\isin DF(k)
j∈DF(k),那么对每个结点
l
∈
D
o
m
(
k
)
l \isin Dom(k)
l∈Dom(k),必定有
j
∈
D
F
(
l
)
j\isin DF(l)
j∈DF(l),除非
l
∈
D
o
m
(
j
)
l \isin Dom(j)
l∈Dom(j)。

首先识别出图中的所有汇合点,对于一个汇合点
j
j
j,我们考察其在CFG中的每个前趋结点。该算法遵循以上三个见解执行。它会定位CFG中的各个汇合点
j
j
j。接下来,对
j
j
j的每个前趋结点p,它会从p开始沿支配者树向上走,直至找到支配
j
j
j的一个结点。根据第二和第三见解,在算法对支配者树的遍历中,除了遍历到的最后一个结点(支配
j
j
j)之外,对其余每个结点
l
l
l都有
j
j
j属于DF(
l
l
l)。这里需要少最簿记工作,以确保任何结点n都只添加到某个结点的支配边界一次。
下图则是本节所用例子,CFG中各个结点的支配边界。

3.3 放置
ϕ
\phi
ϕ函数
有了支配边界之后,编译器可以更精确地判断何处可能需要
ϕ
\phi
ϕ函数。其基本思想是:基本程序块b中对x的定义(x若在多个程序块中活跃),则要求在DF(b)集合包含的每个结点起始处都放置一个对应的
ϕ
\phi
ϕ函数;如果x只是在基本块b中活跃,则在在b的支配边界中插入的
ϕ
\phi
ϕ函数就是多余的。编译器可以计算跨多个程序块的活跃变量名的集合,该集合被称为全局名字(global name)集合。它可以对该集合中的名字插入
ϕ
\phi
ϕ函数,而忽略不在该集合中的名字。
放置
ϕ
\phi
ϕ函数算法如下。Globals是全局名字集合,Blocks(x)包含了所有定义x的基本块,VarKill包含了在当前块中定义的所有变量。

算法(a):首先遍历每个程序块,设当前正在遍历的是b块;遍历b块中的每个形如x <- y op z的操作,若引用的y和z没有在b中定义,将其加入Globals;因为b中现在定义了x,所以将x加入b的VarKill集合中,将b加入Blocks(x)集合中。
算法(b):遍历Globals中的每个全局名字,设当前正在遍历的名字是x,将定义x的所有基本块赋给WorkList;遍历WorkList,设当前遍历的块为b;遍历b的支配边界DF(b),设当前支配边界为块d;如果块d中没有x-
ϕ
\phi
ϕ函数,则插入x-
ϕ
\phi
ϕ函数;最后将d块加入WorkList(由于x-
ϕ
\phi
ϕ在d块中产生了一个新的定义,且x
∈
\isin
∈ Globals,所以需要为d块的支配边界再插入x-(x-
ϕ
\phi
ϕ)函数)。
以下是2.2 活跃变量分析 中的例子,应用以上算法对其插入
ϕ
\phi
ϕ函数。

将算法的处理限于全局名字集合,使其避免了对基本程序块B1中的x和y插入“死亡”的
ϕ
\phi
ϕ函数(B1
∈
\isin
∈ DF(B3),B3包含了对x和y的定义)。但局部名字和全局名字之间的区分不足以避免所有的“死亡”
ϕ
\phi
ϕ函数。例如,B1中b的
ϕ
\phi
ϕ函数是不活跃的,因为在使用b值之前重新定义了b。为避免插入这些
ϕ
\phi
ϕ函数,编译器可以构建LiveOut集合,并在插入
ϕ
\phi
ϕ函数之算法的内层循环中增加一个对变量活跃性的条件判断。
为提高效率,编译器应该避免两种类型的复制。首先,对每个全局名字算法都应该避免将任何基本程序块多次放置到Worklist上。它可以维护一个已经处理的基本程序块的清单,由于算法必须对每个全局名字重置该清单,实现应该使用一种稀疏集或类似的结构。
其次,一个给定的基本程序块可能出现在Worklist上多个结点的支配边界中。如上图9-11所示,算法必须查找这样的基本程序块,以寻找此前已存在的
ϕ
\phi
ϕ函数。为避免这种查找,对指定变量(如x)来说,编译器可以维护一个基本程序块的清单,列出已包含针对该变量
ϕ
\phi
ϕ函数的基本程序块。这需要采用一个稀疏集,针对需要处理的每个全局名字,与Worklist一同重新初始化。
3.4 重命名
下图对过程的支配者树进行了先根次序遍历。在每个基本程序块中,算法首先重命名由程序块顶部的
ϕ
\phi
ϕ函数定义的值,然后按序访问程序块中的各个操作。算法会用当前的SSA形式名(top stack)重写各个操作数,并为操作的结果创建一个新的SSA形式名(push stack)。算法的后一步使得新名字成为当前的名字。在程序块中所有的操作都已经重写之后,算法将使用当前的SSA形式名重写程序块在CFG中各后继结点中的适当
ϕ
\phi
ϕ函数参数。最后,算法对当前程序块在支配者树中的子结点进行递归处理。当算法从这些递归调用返回时,它会将当前静态单赋值形式名的集合恢复到访问当前程序块之前的状态(pop stack)。

上图9-12算法。首先遍历每个全局名字i,将每个名字i的计数器counter[i]初始化为0,每个名字i的栈stack[i]初始化为空;然后以支配者树的root结点为参数调用Rename。算法对每个全局名字i使用了一个计数器(counter是个数组,counter[i]名字i对应的计数器)和一个栈(stack[i]是名字i对应的栈),栈包含了该名字当前SSA形式的下标。在每个定义处,算法通过将目标名字的当前计数器值压栈来产生新的下标,并将计数器加1。因而,名字i栈顶的值总是i当前SSA形式名的下标。下图是对 3.3 放置
ϕ
\phi
ϕ函数 的图9-11例子中B2重命名之前,各个全局变量名的计数器和栈中的值。
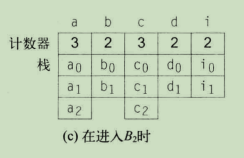
函数NewName的参数为变量名字n。先将n的计数器counter[n]中存放的值赋给i,让counter[n]++,然后将i压入n对应的栈stack[n]中,返回ni。
函数Rename的参数为基本块b。首先遍历块b中的每个操作x <-
ϕ
\phi
ϕ(…),用NewName(x)的返回值重命名x,这一步遍历不管
ϕ
\phi
ϕ的参数;接着遍历块b中的每个操作x <- y op z,依旧用NewName(x)的返回值重命名x,用操作数y和z各自对应栈的栈顶值作为其下标(如y0、z1);再遍历块b在CFG中的后继结点,将所有后继节点的
ϕ
\phi
ϕ参数重命名,编译器必须在这些
ϕ
\phi
ϕ函数中为b按序分配一个参数槽位,在绘制SSA形式时,我们总是假定从左到右的次序,以便匹配从左到右绘制边的次序;然后遍历块b在支配者树中的后继结点,并对每个后继结点递归调用Rename;待块b的后继结点递归结束后,将在块b中定义的所有名字从其对应的栈中弹出。
下图是对 3.3 放置
ϕ
\phi
ϕ函数 的图9-11例子应用以上算法重命名之后的代码。

3.5 从静态单赋值到其他形式的转换
SSA形式到其他形式的转换,保持SSA的名字空间不变,只需要消除掉
ϕ
\phi
ϕ函数,即将其替换为一组复制操作,每个复制操作对应于一条进入当前程序块的边。
以下是替换之前的SSA用例代码。L0中的跳转是条件跳转,L1中的跳转是直接跳转。
L0:
a1 = 1
(cond) => L1, L2
L1:
a2 = 2
=> L2
L2:
a3 = phi(L0 a1, L1 a2)
a4 = ...
...
以下是替换之后的SSA用例代码。L1是直接跳转,从其出发只有L1 -> L2这一条边,所以将a3 = a2复制操作放在跳转之前即可;由于L0是条件跳转,从其出发有L0 -> L1和L0 -> L2两条边,需要再创建一个block L3并让其位于L0和L2之间,则边L3 -> L2具有了唯一性,将a3 = a1的复制操作写入L3即可。
L0:
a1 = 1
(cond) => L1, L3
L1:
a2 = 2
a3 = a2
=> L2
L2:
a4 = ...
...
L3:
a3 = a1
=> L2
例子中的(L0, L2)称为关键边。在CFG中,如果边的源结点具有多个后继结点,而边的目标结点具有多个前趋结点,则称这样的边为关键边。
3.6 使用静态单赋值形式——稀疏简单常量传播
常量传播是现代的编译器中使用最广泛的优化方法之一,它通常应用于高级中间表示(IR)。它解决了在运行时静态检测表达式是否总是求值为唯一常数的问题,如果在调用过程时知道哪些变量将具有常量值,以及这些值将是什么,则编译器可以在编译时期简化常数。常量传播在优化中的几种用途:
- 能在编译时求值的表达式不需要在执行时才求值。如果这样的表达式在循环内,则只需要在编译时进行一次求值而节省执行时间。
- 通过用常量值替换常量变量来修改源程序,这样可以识别然后消除程序的无效代码部分,例如由始终为假的表达式那部分无效代码,从而提高程序的整体效率。
- 过程的部分参数是常量,减少涉及状态向量的大小可以避免代码的扩展,对于控制状态,我们仅存储非常数变量的值。常数值不需要存储,可以始终通过查看控制状态来检索。
- 对从未到达的路径的检测简化了项目的控制流程。简化的控制结构可以帮助将程序转换为适合向量化处理的形式或并行处理的形式。
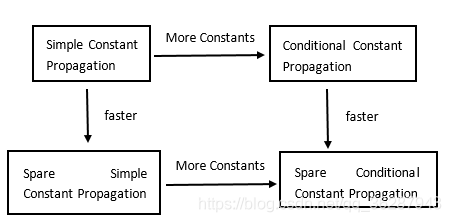
一些编译器在basic block内执行常量传播或在更复杂的控制流中执行恒定传播,很少有编译器通过位域分配执行常量传播或通过指针分配对地址常量执行常量传播。常量传播算法通常有四种:
- 第一种算法由Kildall最早设计出,称为简单常量传播(Simple Constant Propagation)。
- 第二种算法由Reif和Lewis提出,称为稀疏简单常量传播(Sparse Simple Constant Propagation),该算法基于SSA图,由于与SSA图的大小呈线性变化,因此一直未得到广泛使用。
- 第三种算法是Wegbreit算法的一种变体,称为条件常量传播(Conditional Constant Propagation),可以发现所有常量,这些常量可以通过使用所有常量操作数计算所有条件分支来找到,但是它使用相同的输入数据结构,并且渐近于简单常量传播。该算法不能进行死代码消除。
- 第四种算法可以更精确地传播常数及移除无用代码,称之为稀疏条件常量传播(Sparse Conditional Constant Propagation),它可以检测程序中始终会计算为固定值的变量和表达式,并在编译时而不是在运行时计算其值。它与传统的常量传播不同,它依靠静态单一分配(SSA)形式来提高分析稀疏的效率,并且具有检测由于恒定分支条件而永远不会执行的控制流边缘的能力。
编译器使用SSA形式,原因可能是为了改进分析的质量、优化的质量,或者两者兼而有之。我们在SSA形式上进行的全局常量传播(global constant propagation)则是一种使用广泛且质量较高的优化,其采用的是一种名为稀疏简单常量传播(Sparse Simple Constant Propagation,SSCP)的算法。
在SSCP算法中,编译器用一个半格值标注每个SSA形式名。半格有一个底元素(bottom element),记为
⊥
\bot
⊥,还有一个顶元素(top element)记为
⊤
\top
⊤。如下图所示,所有可能的常量值Ci、… 、Cm、及
⊤
\top
⊤和
⊥
\bot
⊥共同构成了半格的集合L。
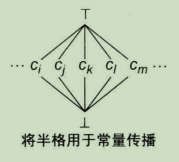
这应用到常量传播上面,
⊤
\top
⊤标注的变量名表示其是一个尚未确定的值(在程序开始执行的时候没有定值),C标注的变量名表示其是一个已知常量值,
⊥
\bot
⊥标注的变量名表示其确定是非常量值。SSCP算法如下图所示,由一个初始化阶段和一个传播阶段组成。

初始化阶段会遍历各个SSA形式名。对于每个SSA形式名n,这一阶段会考察定义n的操作,并根据一组简单的规则来安置Value(n)。
- 如果n是由一个
ϕ
\phi
ϕ函数定义(只有runtime才能确定),或者n的值是未知的(不确定是否为常量),则SSCP将Value(n)设置为
⊤
\top
⊤;
- 如果n的值是一个已知常量Ci,则SSCP将Value(n)设置为Ci;
- 如果n的值不可能是已知的(确定不是常量),如可能是从外部介质读取一个值来定义的,则SSCP将Value(n)设置到
⊥
\bot
⊥。
- 如果Value(n)不是
⊤
\top
⊤,则算法将n添加到Worklist。
传播阶段会从Worklist删除一个静态单赋值形式名n。然后会逐一考察使用了n、同时又定义了某个SSA形式名m的每个操作op。如果Value(m)已经是
⊥
\bot
⊥,则无需进一步的求值处理。否则,算法会将op对应的操作在操作数的格值(latticevalue)上进行解释和计算(能算出结果的算出结果,算不出的继续用格值表示),以便模拟对op操作的求值。如果结果在格中低于Value(m),则相应地下调Value(m)并将m添加到Worklist。该算法在Worklist为空时停止。
四、过程间分析
过程调用引入的低效性有两种起因:一是单过程分析和优化中知识的缺失,是由分析和变换的区域中调用位置的存在引起的;二是为维护过程调用的固有抽象而引入的特定开销。引入过程间分析是为解决前一个问题。
4.1 构建调用图
一个调用图(call graph)是一种控制流图,它表示一个计算机程序中子程序之间的调用关系。调用图的每个节点表示一个过程,每条边(f, g)表示过程f调用过程g。因此,图中的一个循环表示递归过程调用。
如果程序使用值为过程的变量作为参数,则编译器必须分析代码,以估计在每个调用值为过程的变量的调用位置上潜在被调用者的集合。如下图所示,a、b、c和d的值函数指针,作为compose函数的实参,在compose中又利用参数做了函数调用,编译器要能分析代码,找到类似的过程调用。
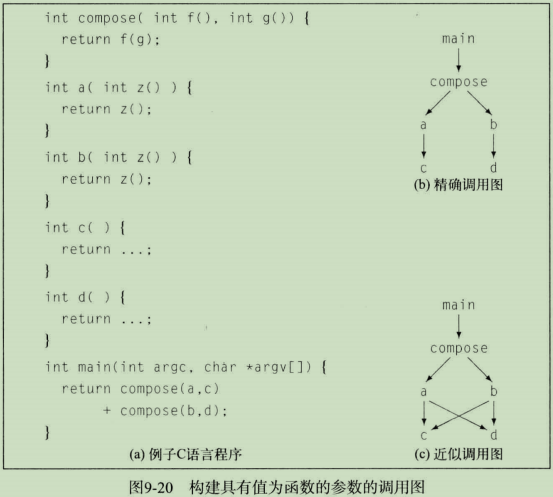
4.2 过程间常量传播
过程间常虽传播会随着全局变量和参数在调用图上的传播跟踪其已知常数值,这种跟踪会穿越过程体并跨越调用图的边。过程间常量传播的目标在于,发现过程总是接收已知常量值的情形,或发现过程总是返回已知常量值的情形。当分析发现这样的常量时,编译器可以对与该值相关的代码进行专门化处理。
过程间常量传播让分析程序发现每个调用位置哪些实参是已知的常数值(3.6 中的SSCP算法可以办到),值为常数的实参沿调用图的边正向传播,算法建立跳跃函数(jump function)来模拟值从调用者流动到被调用者。
具有n个参数的调用位置s会有一个跳跃函数向量
ȷ
s
=
(
ȷ
s
a
,
ȷ
s
b
,
ȷ
s
c
.
.
.
,
ȷ
s
n
)
\jmath_s = (\jmath_s^a, \jmath_s^b, \jmath_s^c ... ,\jmath_s^n)
s=(sa,sb,sc...,sn),其中a是调用者中的第一个形参,b是第二个,依次类推。这些形参是包含S的过程P的形参,每个跳跃函数
ȷ
s
x
\jmath_s^x
sx都依赖于它们的某个子集的值,我们将该集合记作Support(
ȷ
s
x
\jmath_s^x
sx)。
我没有理解上面黄色部分标注的话,导致没有理解跳跃函数,也就没有理解下面算法的第二阶段。等后面看一下英文版将这块内容真正理解之后,再来把算法的解释完善一下。如果好兄弟你从原书看懂了这个算法,请指教!
下图9-21过程间常量传播算法。
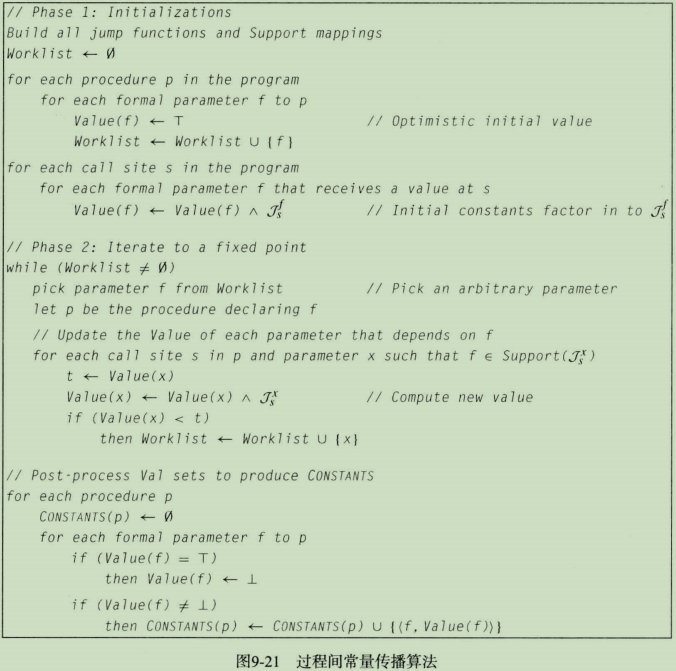
第一阶段,算法将每个过程p的形参f与其字段Value(f)关联。首先遍历程序中的每个过程p,并遍历过程p的每个形参f,将Value(f)都初始化为
⊤
\top
⊤,将f加入Worklist,最终Worklist会包含所有形参。接下来,算法遍历程序中每个调用位置s处的每个实参a,将a对应的形参f的Value字段更新为
V
a
l
u
e
(
f
)
∧
ȷ
s
f
Value(f) \wedge \jmath_s^f
Value(f)∧sf。
第二阶段会重复地从Worklist选择一个形参并传播它。
五、迭代方法
我们优化简介和以上四个小节介绍的都是迭代数据流分析,除此之外还有非迭代数据流分析,如结构性数据流分析(5.1 主要介绍了这个)。5.2 则对可支配算法做了一个优化,现在肝不动了,就不再展开,后面有时间了再来补充,要开始下一章节了。
5.1 结构性数据流算法和可归约性
5.2 加速计算支配性的迭代框架算法的执行