Tarjan算法讲解的博客网上找到三篇比较好的,现在都转载了,个人只研究了第一篇,正如博主所说,讲的标比较详细,清晰,剩下两篇也可以看一下.
卿学姐视频讲解 https://www.bilibili.com/video/av7330663/
全网最详细tarjan算法讲解，我不敢说别的。反正其他tarjan算法讲解，我看了半天才看懂。我写的这个，读完一遍，发现原来tarjan这么简单！
tarjan算法，一个关于 图的联通性的神奇算法。基于DFS（迪法师）算法，深度优先搜索一张有向图。！注意！是有向图。根据树，堆栈，打标记等种种神（che）奇（dan）方法来完成剖析一个图的工作。而图的联通性，就是任督二脉通不通。。的问题。
了解tarjan算法之前你需要知道：
强连通，强连通图，强连通分量，解答树（解答树只是一种形式。了解即可）
不知道怎么办！！！
神奇海螺～：嘟噜噜～！
强连通(strongly connected)： 在一个有向图G里，设两个点 a b 发现，由a有一条路可以走到b，由b又有一条路可以走到a，我们就叫这两个顶点（a，b）强连通。
强连通图： 如果 在一个有向图G中，每两个点都强连通，我们就叫这个图，强连通图。
强连通分量strongly connected components)：在一个有向图G中，有一个子图，这个子图每2个点都满足强连通，我们就叫这个子图叫做 强连通分量 ［分量：：把一个向量分解成几个方向的向量的和，那些方向上的向量就叫做该向量（未分解前的向量）的分量］
举个简单的栗子：
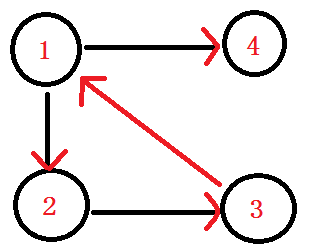
比如说这个图，在这个图中呢，点1与点2互相都有路径到达对方，所以它们强连通.
而在这个有向图中，点1 2 3组成的这个子图，是整个有向图中的强连通分量。
解答树：就是一个可以来表达出递归枚举的方式的树（图），其实也可以说是递归图。。反正都是一个作用，一个展示从“什么都没有做”开始到“所有结求出来”逐步完成的过程。“过程！”
神奇海螺结束！！！
tarjan算法，之所以用DFS就是因为它将每一个强连通分量作为搜索树上的一个子树。而这个图，就是一个完整的搜索树。
为了使这颗搜索树在遇到强连通分量的节点的时候能顺利进行。每个点都有两个参数。
1，DFN［］作为这个点搜索的次序编号（时间戳），简单来说就是 第几个被搜索到的。％每个点的时间戳都不一样％。
2，LOW［］作为每个点在这颗树中的，最小的子树的根，每次保证最小，like它的父亲结点的时间戳这种感觉。如果它自己的LOW［］最小，那这个点就应该从新分配，变成这个强连通分量子树的根节点。
ps：每次找到一个新点，这个点LOW［］＝DFN［］。
而为了存储整个强连通分量，这里挑选的容器是，堆栈。每次一个新节点出现，就进站，如果这个点有 出度 就继续往下找。直到找到底，每次返回上来都看一看子节点与这个节点的LOW值，谁小就取谁，保证最小的子树根。如果找到DFN［］＝＝LOW［］就说明这个节点是这个强连通分量的根节点（毕竟这个LOW［］值是这个强连通分量里最小的。）最后找到强连通分量的节点后，就将这个栈里，比此节点后进来的节点全部出栈，它们就组成一个全新的强连通分量。
先来一段伪代码压压惊：
tarjan(u){
DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值
Stack.push(u) // 将节点u压入栈中
for each (u, v) in E // 枚举每一条边
if (v is not visted) // 如果节点v未被访问过
tarjan(v) // 继续向下找
Low[u] = min(Low[u], Low[v])
else if (v in S) // 如果节点u还在栈内
Low[u] = min(Low[u], DFN[v])
if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
repeat v = S.pop // 将v退栈，为该强连通分量中一个顶点
print v
until (u== v)
}首先来一张有向图。网上到处都是这个图。我们就一点一点来模拟整个算法。
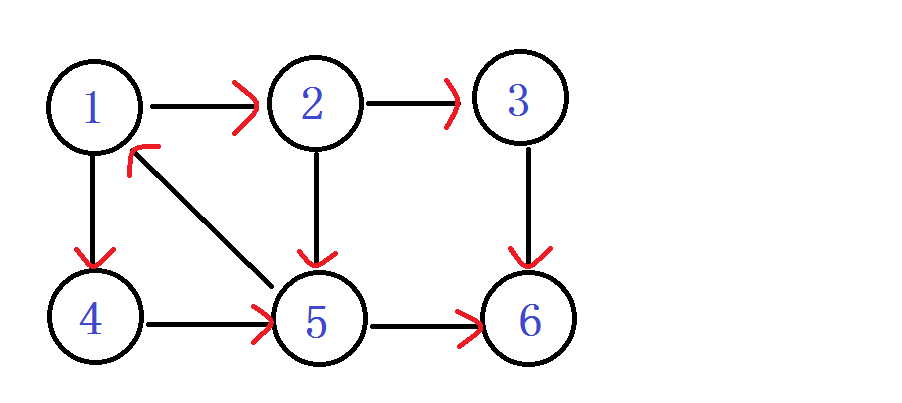
从1进入 DFN［1］＝LOW［1］＝ ＋＋index －－－－1
入栈 1
由1进入2 DFN［2］＝LOW［2］＝ ＋＋index －－－－2
入栈 1 2
之后由2进入3 DFN［3］＝LOW［3］＝ ＋＋index －－－－3
入栈 1 2 3
之后由3进入 6 DFN［6］＝LOW［6］＝＋＋index －－－－4
入栈 1 2 3 6
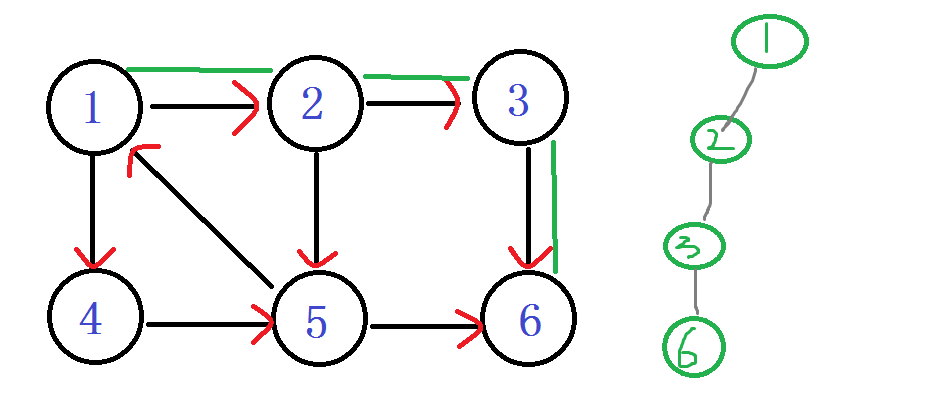
之后发现 嗯？ 6无出度，之后判断 DFN［6］＝＝LOW［6］
说明6是个强连通分量的根节点：6及6以后的点 出栈。
栈： 1 2 3
之后退回 节点3 Low[3] = min(Low[3], Low[6]) LOW［3］还是 3
节点3 也没有再能延伸的边了，判断 DFN［3］＝＝LOW［3］
说明3是个强连通分量的根节点：3及3以后的点 出栈。
栈： 1 2
之后退回 节点2 嗯？！往下到节点5
DFN［5］＝LOW［5］＝ ＋＋index －－－－－5
入栈 1 2 5
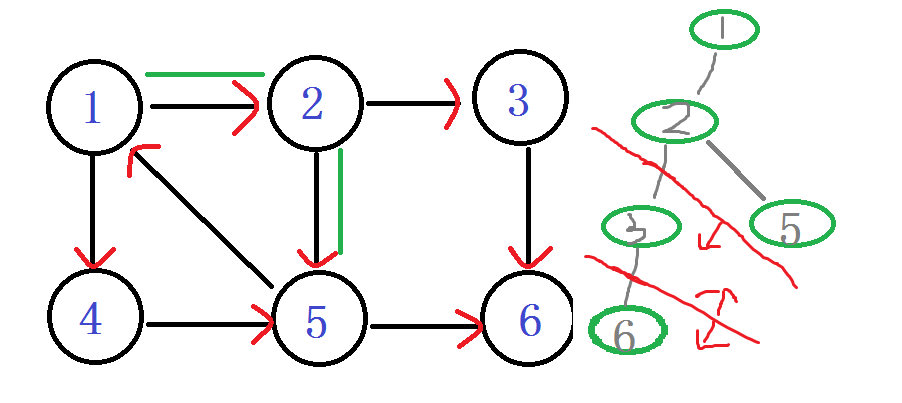
ps：你会发现在有向图旁边的那个丑的（划掉）搜索树 用红线剪掉的子树，那个就是强连通分量子树。每次找到一个。直接。一剪子下去。半个子树就没有了。。
结点5 往下找，发现节点6 DFN［6］有值，被访问过。就不管它。
继续 5往下找，找到了节点1 他爸爸的爸爸。。DFN［1］被访问过并且还在栈中，说明1还在这个强连通分量中，值得发现。 Low[5] = min(Low[5], DFN[1])
确定关系，在这棵强连通分量树中，5节点要比1节点出现的晚。所以5是1的子节点。so
LOW［5］＝ 1
由5继续回到2 Low[2] = min(Low[2], Low[5])
LOW［2］＝1；
由2继续回到1 判断 Low[1] = min(Low[1], Low[2])
LOW［1］还是 1
1还有边没有走过。发现节点4，访问节点4
DFN［4］＝LOW［4］＝＋＋index －－－－6
入栈 1 2 5 4
由节点4，走到5，发现5被访问过了，5还在栈里，
Low[4] = min(Low[4], DFN[5]) LOW［4］＝5
说明4是5的一个子节点。
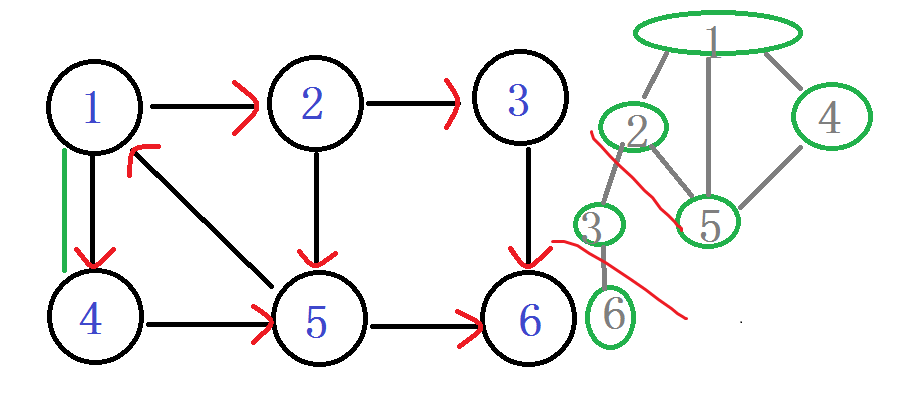
由4回到1.
回到1，判断 Low[1] = min(Low[1], Low[4])
LOW［1］还是 1 。
判断 LOW［1］ ＝＝ DFN［1］
诶？！相等了 说明以1为根节点的强连通分量已经找完了。
将栈中1以及1之后进栈的所有点，都出栈。
栈 ：（鬼都没有了）
这个时候就完了吗？！
你以为就完了吗？！
然而并没有完，万一你只走了一遍tarjan整个图没有找完怎么办呢？！
所以。tarjan的调用最好在循环里解决。
like 如果这个点没有被访问过，那么就从这个点开始tarjan一遍。
因为这样好让每个点都被访问到。
来一道裸代码。
输入：
一个图有向图。
输出：
它每个强连通分量。
这个图就是刚才讲的那个图。一模一样。
input:
6 8
1 3
1 2
2 4
3 4
3 5
4 6
4 1
5 6
output:
6
5
3 4 2 1#include<cstdio>
#include<algorithm>
#include<string.h>
using namespace std;
struct node {
int v,next;
}edge[1001];
int DFN[1001],LOW[1001];
int stack[1001],heads[1001],visit[1001],cnt,tot,index;
void add(int x,int y)
{
edge[++cnt].next=heads[x];
edge[cnt].v = y;
heads[x]=cnt;
return ;
}
void tarjan(int x)//代表第几个点在处理。递归的是点。
{
DFN[x]=LOW[x]=++tot;// 新进点的初始化。
stack[++index]=x;//进站
visit[x]=1;//表示在栈里
for(int i=heads[x];i!=-1;i=edge[i].next)
{
if(!DFN[edge[i].v]) {//如果没访问过
tarjan(edge[i].v);//往下进行延伸，开始递归
LOW[x]=min(LOW[x],LOW[edge[i].v]);//递归出来，比较谁是谁的儿子／父亲，就是树的对应关系，涉及到强连通分量子树最小根的事情。
}
else if(visit[edge[i].v ]){ //如果访问过，并且还在栈里。
LOW[x]=min(LOW[x],DFN[edge[i].v]);//比较谁是谁的儿子／父亲。就是链接对应关系
}
}
if(LOW[x]==DFN[x]) //发现是整个强连通分量子树里的最小根。
{
do{
printf("%d ",stack[index]);
visit[stack[index]]=0;
index--;
}while(x!=stack[index+1]);//出栈，并且输出。
printf("\n");
}
return ;
}
int main()
{
memset(heads,-1,sizeof(heads));
int n,m;
scanf("%d%d",&n,&m);
int x,y;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&x,&y);
add(x,y);
}
for(int i=1;i<=n;i++)
if(!DFN[i]) tarjan(1);//当这个点没有访问过，就从此点开始。防止图没走完
return 0;
}
在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。
如下图中，强连通分量有：{1,2,3,4}，{5}，{6}
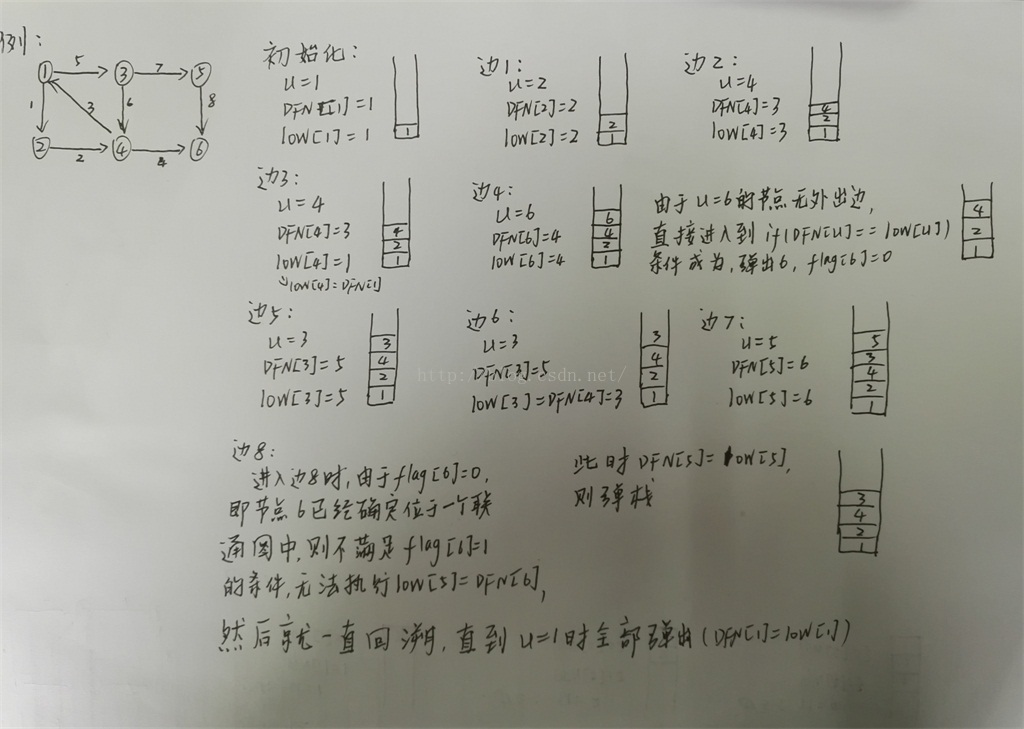
Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。Tarjan算法有点类似于基于后序的深度遍历搜索和并查集的组合，充分利用回溯来解决问题。
在Tarjan算法中为每个节点i维护了以下几个变量：
DFN[i]：深度优先搜索遍历时节点i被搜索的次序。
low[i]：节点i能够回溯到的最早位于栈中的节点。
flag[i]：标记几点i是否在栈中。
Tarjan算法的运行过程：
1.首先就是按照深度优先搜索算法搜索的次序对图中所有的节点进行搜索。
2.在搜索过程中，对于任意节点u和与其相连的节点v，根据节点v是否在栈中来进行不同的操作：
*节点v不在栈中，即节点v还没有被访问过，则继续对v进行深度搜索。
*节点v已经在栈中，即已经被访问过，则判断节点v的DFN值和节点u的low值的大小来更新节点u的low值。如果节点v的 DFN值要小于节点u的low值，根据low值的定义（能够回溯到的最早的已经在栈中的节点），我们需要用DFN值来更新u 的low值。
3.在回溯过程中，对于任意节点u与其子节点v(其实不能算是子节点，只是在深度遍历的过程中，v是在u之后紧挨着u的节点)的 low值来更新节点u的low值。因为节点v能够回溯到的已经在栈中的节点，节点u也一定能够回溯到。因为存在从u到v的直接路 径，所以v能够到的节点u也一定能够到。
4.对于一个连通图，我们很容易想到，在该连通图中有且仅有一个节点u的DFN值和low值相等。该节点一定是在深度遍历的过 程中，该连通图中第一个被访问过的节点，因为它的DFN值和low值最小，不会被该连通图中的其他节点所影响。下面我们证 明为什么仅有一个节点的DFN和low值相等。假设有两个节点的DFN值和low值相等，由于这两个节点的DFN值一定不相同 （DFN值的定义就是深度遍历时被访问的先后
次序），所以两个的low值也绝对不相等。由于位于同一个连通图中，所以两个节点必定相互可达，那么两者的low值一定会 被另外一个所影响（要看谁的low值更小），所以不可能存在两对DFN值和low值相等的节点。
所以我们在回溯的过程中就能够通过判断节点的low值和DFN值是否相等来判断是否已经找到一个子连通图。由于该连通图中 的DFN值和low值相等的节点是该连通图中第一个被访问到的节点，又根据栈的特性，则该节点在最里面。所以能够通过不停 的弹栈，直到弹出该DFN值和low值相同的节点来弹出该连通图中所有的节点。
Tarjan算法的C++实现代码如下，可以配合上面的图加以理解：
#include<iostream>
using namespace std;
int DFN[105]; //记录在做dfs时节点的搜索次序
int low[105]; //记录节点能够找到的最先访问的祖先的记号
int count=1; //标记访问次序，时间戳
int stack[105]; //压入栈中
int top=-1;
int flag[105]; //标记节点是否已经在栈中
int number=0;
int j;
int matrix[105][105]={{0,1,1,0,0,0},{0,0,0,1,0,0},{0,0,0,1,1,0},{1,0,0,0,0,1},{0,0,0,0,0,1},{0,0,0,0,0,0}};
int length; //图的长度
void tarjan(int u){
DFN[u]=low[u]=count++; //初始化两个值，自己为能找到的最先访问的祖先
stack[++top]=u;
flag[u]=1; //标记为已经在栈中
for(int v=0;v<length;v++){
if(matrix[u][v]){
if(!DFN[v]){ //如果点i没有被访问过
tarjan(v); //递归访问
if(low[v]<low[u])
low[u]=low[v]; //更新能找的到祖先
}
else{ //如果访问过了，并且该点的DFN更小，则
if(DFN[v]<low[u]&&flag[v]) //flag[v]这个判断条件很重要，这样可以避免已经确定在其他联通图的v,因为u到v的单向边而影响到u的low
low[u]=DFN[v]; //也就是已经确定了的联通图要剔除掉，剔除的办法就是判断其还在栈中，因为已经确定了的连通图的点
} //flag在下面的do while中已经设为0了(即已经从栈中剔除了)
}
}
//往后回溯的时候，如果发现DFN和low相同的节点，就可以把这个节点之后的节点全部弹栈，构成连通图
if(DFN[u]==low[u]){
number++; //记录连通图的数量
do{
j=stack[top--]; //依次取出，直到u
cout<<j<<" ";
flag[j]=0; //设置为不在栈中
}while(j!=u);
cout<<endl;
}
}
int main(){
memset(DFN,0,sizeof(DFN)); //数据的初始化
memset(low,0,sizeof(low));
memset(flag,0,sizeof(flag));
length=6;
tarjan(0);
cout<<endl;
for(int i=0;i<6;i++){
cout<<"DFN["<<i<<"]:"<<DFN[i]<<" low["<<i<<"]:"<<low[i]<<endl;
}
return 0;
}
[有向图强连通分量]
在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(stronglyconnected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。
下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。
直接根据定义，用双向遍历取交集的方法求强连通分量，时间复杂度为O(N^2+M)。更好的方法是Kosaraju算法或Tarjan算法，两者的时间复杂度都是O(N+M)。本文介绍的是Tarjan算法。
[Tarjan算法]
Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。由定义可以得出，
| Low(u)=Min{DFN(u),Low(v),(u,v)为树枝边，u为v的父节点 |
当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。
算法伪代码如下
tarjan(u)
{
DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值
Stack.push(u) // 将节点u压入栈中
for each (u, v) in E // 枚举每一条边
if (v is not visted) // 如果节点v未被访问过
tarjan(v) // 继续向下找
Low[u] = min(Low[u], Low[v])
else if (v in S) // 如果节点u还在栈内
Low[u] = min(Low[u], DFN[v])
if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
repeat
v = S.pop // 将v退栈，为该强连通分量中一个顶点
print v
until (u== v)
}接下来是对算法流程的演示。
从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。
返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。
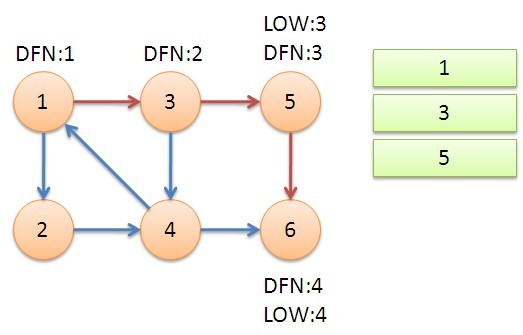
返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4像节点1的后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，不再访问6，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。
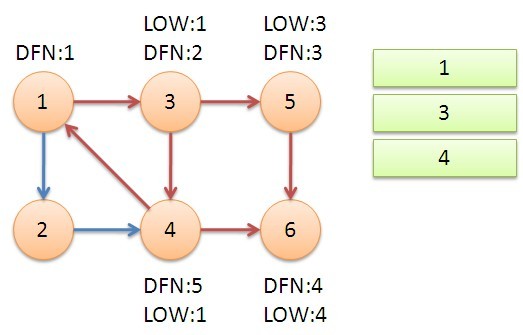
继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=4。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。
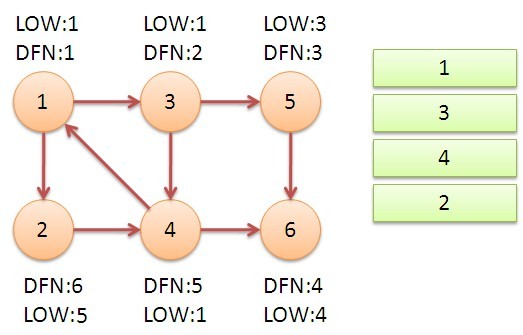
至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。
可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。
求有向图的强连通分量还有一个强有力的算法，为Kosaraju算法。Kosaraju是基于对有向图及其逆图两次DFS的方法，其时间复杂度也是 O(N+M)。与Trajan算法相比，Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS，不用建立逆图，更简洁。 在实际的测试中，Tarjan算法的运行效率也比Kosaraju算法高30%左右。此外，该Tarjan算法与求无向图的双连通分量(割点、桥)的Tarjan算法也有着很深的联系。学习该Tarjan算法，也有助于深入理解求双连通分量的Tarjan算法，两者可以类比、组合理解。
求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法，以及求最近公共祖先的离线Tarjan算法，在此对Tarjan表示崇高的敬意。
代码:
void tarjan(int i)
{
int j;
DFN[i]=LOW[i]=++Dindex;
instack[i]=true;
Stap[++Stop]=i;
for (edge *e=V[i]; e; e=e->next)
{
j=e->t;
if (!DFN[j])
{
tarjan(j);
if (LOW[j]<LOW[i])
LOW[i]=LOW[j];
}
else if (instack[j] && DFN[j]<LOW[i])
LOW[i]=DFN[j];
}
if (DFN[i]==LOW[i])
{
Bcnt++;
do
{
j=Stap[Stop--];
instack[j]=false;
Belong[j]=Bcnt;
}
while (j!=i);
}
}
void solve()
{
int i;
Stop=Bcnt=Dindex=0;
memset(DFN,0,sizeof(DFN));
for (i=1; i<=N; i++)
if (!DFN[i])
tarjan(i);
}