[算法]
输入:
T
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
⋯
,
(
x
N
,
y
N
)
}
,
x
1
∈
R
n
,
y
∈
{
+
1
,
−
1
}
,
i
=
1
,
2
,
⋯
,
N
T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\},x_1\in R^n,y\in\{+1,-1\},i=1,2,\cdots,N
T={(x1,y1),(x2,y2),⋯,(xN,yN)},x1∈Rn,y∈{+1,−1},i=1,2,⋯,N
输出:
最大间隔分离超平面和决策函数
(1)构建优化问题: { min ω , b 1 2 ∣ ∣ ω ∣ ∣ 2 s . t . 1 − y i ( ω ⋅ x i + b ) ≤ 0 \left\{ \begin{split} &\min_{\omega,b}\frac{1}{2}||\omega||^2\\ &s.t.\quad 1-y_i(\omega\cdot x_i+b)\leq0 \end{split} \right. ⎩ ⎨ ⎧ω,bmin21∣∣ω∣∣2s.t.1−yi(ω⋅xi+b)≤0
注意:与之前 min ω , b ∣ ∣ ω ∣ ∣ \min_{\omega,b}||\omega|| minω,b∣∣ω∣∣有区别, min ω , b ∣ ∣ ω ∣ ∣ \min_{\omega,b}||\omega|| minω,b∣∣ω∣∣等价于 min ω , b ∣ ∣ ω ∣ ∣ 2 \min_{\omega,b}||\omega||^2 minω,b∣∣ω∣∣2, 1 2 \frac{1}{2} 21是未来求导后消掉2。优化问题所得的解为: ω ∗ , b ∗ \omega^{*},b^{*} ω∗,b∗。
(2)输出结果
分离超平面: ω ∗ ⋅ x + b ∗ = 0 \omega^{*}\cdot x+b^{*}=0 ω∗⋅x+b∗=0
决策函数: f ( x ) = s i g n ( ω ∗ ⋅ x + b ∗ ) f(x)=sign(\omega^{*}\cdot x+b^{*}) f(x)=sign(ω∗⋅x+b∗)
我们有一组实例点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),有下面的分类情况: { ω ∗ ⋅ x 0 + b ∗ > 0 ⇒ y 0 = + 1 ω ∗ ⋅ x 0 + b ∗ < 0 ⇒ y 0 = − 1 \left\{ \begin{split} &\omega^{*}\cdot x_0+b^{*}>0\Rightarrow y_0=+1\\ &\omega^{*}\cdot x_0+b^{*}<0\Rightarrow y_0=-1 \end{split} \right. {ω∗⋅x0+b∗>0⇒y0=+1ω∗⋅x0+b∗<0⇒y0=−1
我们接下来看一个例子:
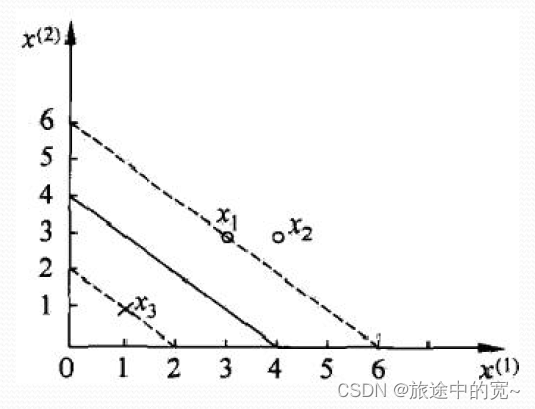
已知一个如上图所示的训练数据集,其正例点是 x 1 = ( 3 , 3 ) T , x 2 = ( 4 , 3 ) T x_1=(3,3)^T,x_2=(4,3)^T x1=(3,3)T,x2=(4,3)T,负例点是 x 3 = ( 1 , 1 ) T x_3=(1,1)^T x3=(1,1)T,试求最大间隔分离超平面。
解
H 1 H_1 H1正例所对应的超平面为: ω ⋅ x + b = 1 \omega\cdot x+b=1 ω⋅x+b=1; H 2 H_2 H2负例对应的超平面为: ω ⋅ x + b = − 1 \omega\cdot x+b=-1 ω⋅x+b=−1。
H 1 H_1 H1与 H 2 H_2 H2之间的距离称为最优间隔,为: 2 ∣ ∣ ω ∣ ∣ \frac{2}{||\omega||} ∣∣ω∣∣2, H 1 H_1 H1与 H 2 H_2 H2为间隔边界。
我们设 ω = ( ω 1 , ω 2 ) T \omega=(\omega_1,\omega_2)^T ω=(ω1,ω2)T。
(1)优化问题 min ω , b 1 2 ∣ ∣ ω ∣ ∣ 2 = 1 2 ω 1 2 + 1 2 ω 2 2 s . t . 1 − y i ( ω ⋅ x i + b ) ≤ 0 , i = 1 , 2 , 3 \begin{split} &\min_{\omega,b}\frac{1}{2}||\omega||^2=\frac{1}{2}\omega_1^2+\frac{1}{2}\omega_2^2\\ &s.t.\quad 1-y_i(\omega\cdot x_i+b)\leq0,i=1,2,3 \end{split} ω,bmin21∣∣ω∣∣2=21ω12+21ω22s.t.1−yi(ω⋅xi+b)≤0,i=1,2,3
面对这个问题,我们的约束条件分别为: { 1 − 1 × ( 3 ω 1 + 3 ω 2 + b ) ≤ 0 1 − 1 × ( 4 ω 1 + 3 ω 2 + b ) ≤ 0 1 − ( − 1 ) × ( ω 1 + ω 2 + b ) ≤ 0 \left\{ \begin{split} &1-1\times(3\omega_1+3\omega_2+b)\leq0\\ &1-1\times(4\omega_1+3\omega_2+b)\leq0\\ &1-(-1)\times(\omega_1+\omega_2+b)\leq0 \end{split} \right. ⎩ ⎨ ⎧1−1×(3ω1+3ω2+b)≤01−1×(4ω1+3ω2+b)≤01−(−1)×(ω1+ω2+b)≤0
{ 1 − ( 3 ω 1 + 3 ω 2 + b ) = 0 1 + ( ω 1 + ω 2 + b ) = 0 ⇒ ω 1 + ω 2 = 1 \left\{ \begin{split} &1-(3\omega_1+3\omega_2+b)=0\\ &1+(\omega_1+\omega_2+b)=0\\ \end{split} \right. \Rightarrow \omega_1+\omega_2=1 {1−(3ω1+3ω2+b)=01+(ω1+ω2+b)=0⇒ω1+ω2=1
我们得到: 1 2 ω 1 2 + 1 2 ω 2 2 = 1 2 ( 1 − ω 1 ) 2 = ω 1 2 − ω + 1 2 \begin{split} \frac{1}{2}\omega_1^2+\frac{1}{2}\omega_2^2&=\frac{1}{2}(1-\omega_1)^2\\ &=\omega_1^2-\omega+\frac{1}{2} \end{split} 21ω12+21ω22=21(1−ω1)2=ω12−ω+21
当 ω 1 = 1 2 \omega_1=\frac{1}{2} ω1=21时上式取得最小值,此时 ω 2 = 1 2 \omega_2=\frac{1}{2} ω2=21
我们得到的超平面为: 1 2 x ( 1 ) + 1 2 x ( 2 ) = 2 \frac{1}{2}x^{(1)}+\frac{1}{2}x^{(2)}=2 21x(1)+21x(2)=2
优化问题: min ω , b 1 2 ∣ ∣ ω ∣ ∣ 2 s . t . y i ( ω ⋅ x i + b ) − 1 ≥ 0 , i = 1 , 2 , ⋯ , N \begin{split} &\min_{\omega,b}\frac{1}{2}||\omega||^2\\ &s.t.\quad y_i(\omega\cdot x_i+b)-1\geq0,i=1,2,\cdots,N \end{split} ω,bmin21∣∣ω∣∣2s.t.yi(ω⋅xi+b)−1≥0,i=1,2,⋯,N
上面的问题是包含不等式约束的凸优化问题。
我们可以找到一个广义拉格朗日函数,约束放到拉格朗日函数中,其中,
α
\alpha
α为
N
N
N个拉格朗日乘子。
L
(
ω
,
b
,
α
)
=
1
2
∣
∣
ω
∣
∣
2
+
∑
i
=
1
N
α
i
(
1
−
y
i
(
ω
⋅
x
i
+
b
)
)
=
1
2
∣
∣
ω
∣
∣
2
−
∑
i
=
1
N
α
i
y
i
(
ω
⋅
x
i
+
b
)
+
∑
i
=
1
N
α
i
\begin{split} L(\omega,b,\alpha)&=\frac{1}{2}||\omega||^2+\sum_{i=1}^{N}\alpha_i(1-y_i(\omega\cdot x_i+b))\\ &=\frac{1}{2}||\omega||^2-\sum_{i=1}^{N}\alpha_iy_i(\omega\cdot x_i+b)+\sum_{i=1}^{N}\alpha_i \end{split}
L(ω,b,α)=21∣∣ω∣∣2+i=1∑Nαi(1−yi(ω⋅xi+b))=21∣∣ω∣∣2−i=1∑Nαiyi(ω⋅xi+b)+i=1∑Nαi
拆成两部分是为了方便后续对偶问题的计算。
α = ( α 1 , α 2 , ⋯ , α N ) T \alpha=(\alpha_1,\alpha_2,\cdots,\alpha_N)^T α=(α1,α2,⋯,αN)T, α i ≥ 0 \alpha_i\geq0 αi≥0。
我们的原始问题为: min ω , b max α L ( ω , b , α ) \min_{\omega,b}\;\max_{\alpha}\;L(\omega,b,\alpha) ω,bminαmaxL(ω,b,α)
对偶问题为: max α min ω , b L ( ω , b , α ) \max_{\alpha}\;\min_{\omega,b}\;L(\omega,b,\alpha) αmaxω,bminL(ω,b,α)
方便起见,我们可以用 θ D ( α ) = min ω , b L ( ω , b , α ) \theta_{D}(\alpha)=\min_{\omega,b}\;L(\omega,b,\alpha) θD(α)=minω,bL(ω,b,α),其中 D D D为对偶的含义。
对偶问题拆成两部分:
第一部分:内部极小化 θ D ( α ) \theta_{D}(\alpha) θD(α): ∇ ω L = 1 2 × 2 ⋅ ω − ∑ i = 1 N α i y i x i = ω − ∑ i = 1 N α i y i x i = 0 ∇ b L = − ∑ i = 1 N α i y i = 0 \begin{split} \nabla_{\omega}\;L&=\frac{1}{2}\times 2\cdot \omega-\sum_{i=1}^{N}\alpha_iy_ix_i\\ &=\omega-\sum_{i=1}^{N}\alpha_iy_ix_i=0\\ \nabla_{b}\;L&=-\sum_{i=1}^{N}\alpha_iy_i=0 \end{split} ∇ωL∇bL=21×2⋅ω−i=1∑Nαiyixi=ω−i=1∑Nαiyixi=0=−i=1∑Nαiyi=0
从上面的梯度计算我们可以得到: { ω = ∑ i = 1 N α i y i x i ∑ i = 1 N α i y i = 0 \left\{ \begin{split} &\omega=\sum_{i=1}^{N}\alpha_iy_ix_i\\ &\sum_{i=1}^{N}\alpha_iy_i=0 \end{split} \right. ⎩ ⎨ ⎧ω=i=1∑Nαiyixii=1∑Nαiyi=0
我们代入广义拉格朗日函数为: θ D ( α ) ⇒ 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i y i ( ∑ j = 1 N α j y j ( x j ⋅ x i ) ) + ∑ i = 1 N α i = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i \begin{split} &\theta_{D}(\alpha)\\ \Rightarrow &\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^{N}\alpha_iy_i(\sum_{j=1}^{N}\alpha_jy_j(x_j\cdot x_i))+\sum_{i=1}^{N}\alpha_i\\ =&-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^{N}\alpha_i \end{split} ⇒=θD(α)21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαiyi(j=1∑Nαjyj(xj⋅xi))+i=1∑Nαi−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαi
第二部分:外部极大化问题 { max α θ D ( α ) s . t . { ∑ i = 1 N α i y i = 0 α i ≥ 0 i = 1 , 2 , ⋯ , N \left\{ \begin{split} &\max_{\alpha}\;\theta_{D}(\alpha)\\ &s.t.\;\left\{ \begin{split} &\sum_{i=1}^{N}\alpha_iy_i=0\\ &\alpha_i\geq0\\ &i=1,2,\cdots,N \end{split} \right. \end{split} \right. ⎩ ⎨ ⎧αmaxθD(α)s.t.⎩ ⎨ ⎧i=1∑Nαiyi=0αi≥0i=1,2,⋯,N
但是 α ∗ \alpha^{*} α∗如何得到 ω ∗ \omega^{*} ω∗和 b ∗ b^{*} b∗?
在解决这个问题之前,我们先看一下什么叫原始问题和对偶问题,以及求解需要满足的KKT条件。
在约束最优化问题中,常常利用拉格朗日对偶性将原始问题转换为对偶问题,通过解对偶问题得到原始问题的解。
[原始问题]
设 f ( x ) , c ( x ) , h ( x ) f(x),c(x),h(x) f(x),c(x),h(x)是定义在 R n R^n Rn上的连续可微函数: min x ∈ R n f ( x ) s . t . { c i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , k h j ( x ) = 0 , j = 1 , 2 , ⋯ , l \begin{split} &\min_{x\in R^n}\;f(x)\\ &s.t.\;\left\{ \begin{split} &c_i(x)\leq0,i=1,2,\cdots,k\\ &h_j(x)=0,j=1,2,\cdots,l \end{split} \right. \end{split} x∈Rnminf(x)s.t.{ci(x)≤0,i=1,2,⋯,khj(x)=0,j=1,2,⋯,l
引进拉格朗日函数,
α
i
,
β
j
\alpha_i,\beta_j
αi,βj为乘子,
α
i
≥
0
\alpha_i\geq0
αi≥0
L
(
x
,
α
,
β
)
=
f
(
x
)
+
∑
i
=
1
k
α
i
c
i
(
x
)
+
∑
i
=
1
l
β
j
h
j
(
x
)
L(x,\alpha,\beta)=f(x)+\sum_{i=1}^{k}\alpha_ic_i(x)+\sum_{i=1}^{l}\beta_jh_j(x)
L(x,α,β)=f(x)+i=1∑kαici(x)+i=1∑lβjhj(x)
假设给定某个 x x x,如果 x x x违反约束条件: c i ( ω ) > 0 , h j ( ω ) ≠ 0 ⇒ θ p ( x ) = max α , β : α i ≥ 0 [ f ( x ) + ∑ i = 1 k α i c i ( x ) + ∑ j = 1 l β j h j ( x ) ] = + ∞ \begin{split} &c_i(\omega)>0,h_j(\omega)\neq0\\ \Rightarrow &\theta_p(x)=\max_{\alpha,\beta:\alpha_i\geq0}[f(x)+\sum_{i=1}^{k}\alpha_ic_i(x)+\sum_{j=1}^{l}\beta_jh_j(x)]=+\infty \end{split} ⇒ci(ω)>0,hj(ω)=0θp(x)=α,β:αi≥0max[f(x)+i=1∑kαici(x)+j=1∑lβjhj(x)]=+∞
θ p ( x ) = { f ( x ) , x ∈ s . t . + ∞ , o t h e r w i s e \theta_p(x)=\left\{ \begin{split} &f(x)\;,\;x\in s.t.\\ &+\infty\;,\;otherwise \end{split} \right. θp(x)={f(x),x∈s.t.+∞,otherwise
考虑极小问题:
min
x
θ
p
(
x
)
=
min
x
max
α
,
β
:
α
i
≥
0
L
(
x
,
α
,
β
)
\min_{x}\;\theta_p(x)=\min_{x}\;\max_{\alpha,\beta:\alpha_i\geq0}\;L(x,\alpha,\beta)
xminθp(x)=xminα,β:αi≥0maxL(x,α,β)
与原始最优化问题等价: p ∗ = min x θ p ( x ) p^{*}=\min_{x}\;\theta_{p}(x) p∗=xminθp(x)
总结如下:
原始问题总结为:
min
x
θ
p
(
x
)
=
min
x
max
α
,
β
:
α
i
≥
0
L
(
x
,
α
,
β
)
\min_{x}\;\theta_{p}(x)=\min_{x}\;\max_{\alpha,\beta:\alpha_{i}\geq0}\;L(x,\alpha,\beta)
xminθp(x)=xminα,β:αi≥0maxL(x,α,β)
称为广义拉格朗日函数的极小极大问题。
定义原始问题的最优值: p ∗ = min x θ p ( x ) p^{*}=\min_{x}\;\theta_{p}(x) p∗=xminθp(x)
[对偶问题]
定义: θ D ( α , β ) = min x L ( x , α , β ) \theta_{D}(\alpha,\beta)=\min_{x}\;L(x,\alpha,\beta) θD(α,β)=xminL(x,α,β)
则最大值问题:
max
α
,
β
:
α
i
≥
0
θ
D
(
α
,
β
)
=
max
α
,
β
:
α
i
≥
0
min
x
L
(
x
,
α
,
β
)
\max_{\alpha,\beta:\alpha_i\geq0}\theta_{D}(\alpha,\beta)=\max_{\alpha,\beta:\alpha_i\geq0}\;\min_{x}\;L(x,\alpha,\beta)
α,β:αi≥0maxθD(α,β)=α,β:αi≥0maxxminL(x,α,β)
上述称为广义拉格朗日函数的极大极小问题。
表示为约束最优化问题: { max α , β θ D ( α , β ) = max α , β min x L ( x , α , β ) s . t . α i ≥ 0 , i = 1 , 2 , ⋯ , k \left\{ \begin{split} &\max_{\alpha,\beta}\;\theta_{D}(\alpha,\beta)=\max_{\alpha,\beta}\;\min_{x}\;L(x,\alpha,\beta)\\ &s.t.\;\alpha_i\geq0,i=1,2,\cdots,k \end{split} \right. ⎩ ⎨ ⎧α,βmaxθD(α,β)=α,βmaxxminL(x,α,β)s.t.αi≥0,i=1,2,⋯,k
称为原始问题的对偶问题。
对偶问题的最优值:
d
∗
=
max
α
,
β
:
α
i
≥
0
θ
D
(
α
,
β
)
d^{*}=\max_{\alpha,\beta:\alpha_i\geq0}\;\theta_{D}(\alpha,\beta)
d∗=α,β:αi≥0maxθD(α,β)
[原始问题和对偶问题的关系]
若原始问题和对偶问题都有最优值,则:
d
∗
=
max
α
,
β
:
α
i
≥
0
min
x
L
(
x
,
α
,
β
)
≤
min
x
max
α
,
β
:
α
i
≥
0
L
(
x
,
α
,
β
)
=
p
∗
d^{*}=\max_{\alpha,\beta:\alpha_i\geq0}\min_{x}\;L(x,\alpha,\beta)\leq\min_{x}\;\max_{\alpha,\beta:\alpha_i\geq0}\;L(x,\alpha,\beta)=p^{*}
d∗=α,β:αi≥0maxxminL(x,α,β)≤xminα,β:αi≥0maxL(x,α,β)=p∗
推论:
设
x
∗
x^{*}
x∗,和
α
∗
\alpha^{*}
α∗,
β
∗
\beta^{*}
β∗分别是原始问题和对偶问题的可行解,并且
d
∗
=
p
∗
d^{*}=p^{*}
d∗=p∗,则
x
∗
x^{*}
x∗,和
α
∗
\alpha^{*}
α∗,
β
∗
\beta^{*}
β∗分别是原始问题和对偶问
题的最优解。
[KKT条件]
对原始问题和对偶问题,假设函数
f
(
x
)
f(x)
f(x)和
c
i
(
x
)
c_i(x)
ci(x)是凸函数,
h
j
(
x
)
h_j(x)
hj(x)是仿射函数,并且不等式
c
i
(
x
)
c_i(x)
ci(x)是严格可行的,则
x
∗
x^{*}
x∗,和
α
∗
\alpha^{*}
α∗,
β
∗
\beta^{*}
β∗分别是原始问题和对偶问题的解的充分必要条件是
x
∗
x^{*}
x∗,和
α
∗
\alpha^{*}
α∗,
β
∗
\beta^{*}
β∗满足KKT条件。
∇
x
L
(
x
∗
,
α
∗
,
β
∗
)
=
0
∇
α
L
(
x
∗
,
α
∗
,
β
∗
)
=
0
∇
β
L
(
x
∗
,
α
∗
,
β
∗
)
=
0
α
i
∗
c
i
(
x
∗
)
=
0
,
i
=
1
,
2
,
⋯
,
k
c
i
(
x
∗
)
≤
0
,
i
=
1
,
2
,
⋯
,
k
α
i
∗
≥
0
,
i
=
1
,
2
,
⋯
,
k
h
j
(
x
∗
)
=
0
,
j
=
1
,
2
,
⋯
,
l
\begin{split} &\nabla_{x}\;L(x^{*},\alpha^{*},\beta^{*})=0\\ &\nabla_{\alpha}\;L(x^{*},\alpha^{*},\beta^{*})=0\\ &\nabla_{\beta}\;L(x^{*},\alpha^{*},\beta^{*})=0\\ &\alpha_{i}^{*}c_{i}(x^{*})=0\;,\;i=1,2,\cdots,k\\ &c_{i}(x^{*})\leq0\;,\;i=1,2,\cdots,k\\ &\alpha_{i}^{*}\geq0\;,\;i=1,2,\cdots,k\\ &h_j(x^{*})=0\;,\;j=1,2,\cdots,l \end{split}
∇xL(x∗,α∗,β∗)=0∇αL(x∗,α∗,β∗)=0∇βL(x∗,α∗,β∗)=0αi∗ci(x∗)=0,i=1,2,⋯,kci(x∗)≤0,i=1,2,⋯,kαi∗≥0,i=1,2,⋯,khj(x∗)=0,j=1,2,⋯,l
我们上式中的
c
i
(
x
)
=
1
−
y
i
(
ω
⋅
x
i
+
b
)
c_i(x)=1-y_i(\omega\cdot x_i+b)
ci(x)=1−yi(ω⋅xi+b),其中
α
\alpha
α相当于
ω
\omega
ω。
∇
ω
L
=
ω
−
∑
i
=
1
N
α
i
y
i
x
i
=
0
⇒
ω
∗
=
∑
i
=
1
N
α
i
∗
y
i
x
i
\begin{split} \nabla_{\omega}\;L&=\omega-\sum_{i=1}^{N}\alpha_iy_ix_i=0\\ \Rightarrow \omega^{*}&=\sum_{i=1}^{N}\alpha_i^{*}y_ix_i \end{split}
∇ωL⇒ω∗=ω−i=1∑Nαiyixi=0=i=1∑Nαi∗yixi
b ∗ b^{*} b∗应该如何表示呢?
如果 α ∗ = ( 0 , 0 , ⋯ , 0 ) T ⇒ ω ∗ = 0 \alpha^{*}=(0,0,\cdots,0)^T \Rightarrow \omega^{*}=0 α∗=(0,0,⋯,0)T⇒ω∗=0,不符合要求。
所以存在 α j ∗ > 0 \alpha_j^{*}>0 αj∗>0,使得: α j ∗ ( 1 − y j ( ω ∗ ⋅ x j + b ∗ ) ) = 0 ⇒ 1 − y j ( ω ∗ ⋅ x j + b ∗ ) = 0 ⇒ b ∗ = 1 y j − ω ∗ ⋅ x j = 1 y j − ∑ i = 1 N α i y i ( x i ⋅ x j ) \begin{split} &\alpha_j^{*}(1-y_j(\omega^{*}\cdot x_j+b^{*}))=0\\ \Rightarrow &1-y_j(\omega^{*}\cdot x_j+b^{*})=0\\ \Rightarrow &b^{*}=\frac{1}{y_j}-\omega^{*}\cdot x_j=\frac{1}{y_j}-\sum_{i=1}^{N}\alpha_iy_i(x_i\cdot x_j) \end{split} ⇒⇒αj∗(1−yj(ω∗⋅xj+b∗))=01−yj(ω∗⋅xj+b∗)=0b∗=yj1−ω∗⋅xj=yj1−i=1∑Nαiyi(xi⋅xj)
所以我们得到
b
∗
b^{*}
b∗的表达式为:
b
∗
=
y
j
−
∑
i
=
1
N
α
i
∗
y
i
(
x
i
⋅
x
j
)
b^{*}=y_j-\sum_{i=1}^{N}\alpha_i^{*}y_i(x_i\cdot x_j)
b∗=yj−i=1∑Nαi∗yi(xi⋅xj)
我们的超平面为: ω ∗ ⋅ x + b ∗ = 0 \omega^{*}\cdot x+b^{*}=0 ω∗⋅x+b∗=0
我们的决策函数为: f ( x ) = s i g n ( ω ∗ ⋅ x + b ∗ ) f(x)=sign(\omega^{*}\cdot x+b^{*}) f(x)=sign(ω∗⋅x+b∗)
