【高等数学重点题型篇】——一元函数微分学的应用

本文仅用于个人学习记录，使用的教材为汤家凤老师的《高等数学辅导讲义》。本文无任何盈利或者赚取个人声望的目的，如有侵权，请联系删除！

一、证明f   ( n ) \ ^{(n)}  (n)(ξ) = 0

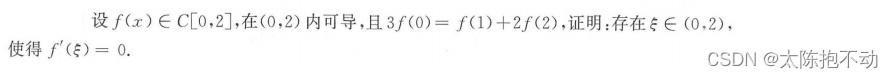
本题除了需要用到罗尔定理外，还需结合连续函数的性质来证明。

本题构造一个函数F(x)，利用拉格朗日中值定理和罗尔定理来证明。

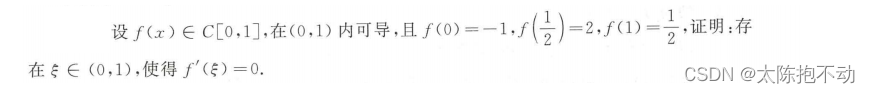
本题有两种方法，一种是构造函数使用零点定理，另一种是直接使用最值定理。

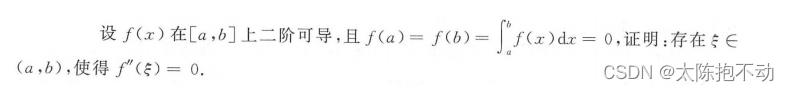
二、待证结论中只有一个中值ξ，不含其他字母

这类问题通常有三种方法构造辅助函数，分别是还原法，分组构造法和凑微分法。

2.1 还原法

若待证结论为f’(ξ) + f²(ξ) = 0，则辅助函数构造如下

• 将f’(ξ) + f²(ξ) = 0写为f’(x) + f²(x) = 0。
• 将f’(x) + f²(x) = 0改写为 f ′ ( x ) f ( x ) \frac{f'(x)}{f(x)} f(x)f′(x)​ + f(x) = 0。
• 将 f ′ ( x ) f ( x ) \frac{f'(x)}{f(x)} f(x)f′(x)​ + f(x) = 0还原得[lnf(x)]’ + [ ∫ 0 x f ( t ) d t \int_0^xf(t)dt ∫0x​f(t)dt]’ = 0。

最终辅助函数为φ(x) = f(x)e   ∫ 0 x f ( t ) d t \ ^{\int_0^xf(t)dt}  ∫0x​f(t)dt

若待证结论为f’(ξ) + 2f(ξ) = 0，则辅助函数构造如下

• 将f’(ξ) + 2f(ξ) = 0写为f’(x) + 2f(x) = 0。
• 将f’(x) + 2f(x) = 0改写为 f ′ ( x ) f ( x ) \frac{f'(x)}{f(x)} f(x)f′(x)​ + 2 = 0。
• 将 f ′ ( x ) f ( x ) \frac{f'(x)}{f(x)} f(x)f′(x)​ + 2 = 0还原得[lnf(x)]’ + (2x)’ = 0。

最终辅助函数为φ(x) = e   2 x \ ^{2x}  2xf(x)。

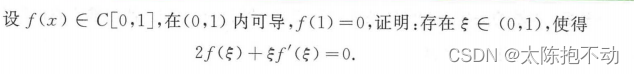
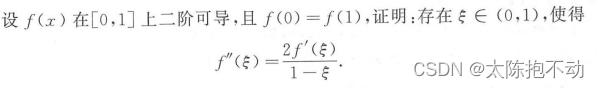
本题需要补充一个积分中值定理

设函数f(x) ∈ C(a,b)，存在ξ ∈ (a,b)，使得 ∫ a b \int_a^b ∫ab​f(x)dx = f(ξ)(b - a)，其中ξ ∈ [a,b]。

2.2 分组构造法

所谓分组构造法就是将所证结论进行适当的分组，然后分别使用还原法构造辅助函数。

若所论证的结论为f’(ξ) - f(ξ) + 2ξ = 2，则辅助函数构造方法如下

• 将f’(ξ) - f(ξ) + 2ξ = 2改写为f’(x) - f(x) + 2x = 2。
• 将f’(x) - f(x) + 2x = 2分组为[f’(x) - 2x]’ - [f(x) - 2x] = 0。

最终辅助函数为φ(x) = e   − x \ ^{-x}  −x[f(x) - 2x]。

若所论证结论为f’'(ξ) - f(ξ) = 0，则辅助函数构造方法如下

• 将f’‘(ξ) - f(ξ) = 0改写为f’'(x) - f(x) = 0。
• 将f’‘(x) - f(x) = 0分组为f’‘(x) - f’(x) + f’(x) - f(x) = 0。

最终辅助函数为φ(x) = e^x [f’(x) - f(x)]。

若所证结论为f’‘(ξ) + f’(ξ) = 2，则辅助函数构造方法如下

• 将f’‘(ξ) + f’(ξ) = 2改写为f’‘(x) + f’(x) = 2。
• 将f’‘(x) + f’(x) = 2分组为[f’(x) - 2]’ + [f’(x) - 2] = 0。

最终辅助函数为φ(x) = e^x [f’(x) - 2]。

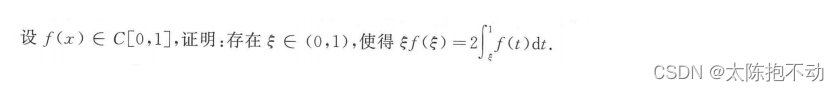
本题并未使用分组构造法，而是直接可以看出辅助函数。

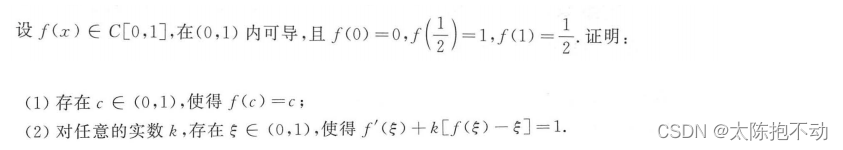
2.3 凑微分法

所谓凑微分法就是先将结论中的ξ变成x，再去分母、移项，整理成g(x) = 0的形式，再找出φ’(x) = g(x)，φ(x)即为辅助函数。

三、结论中含ξ，含a，b

3.1 a，b与ξ可分离

这类问题主要有以下两个思路

• 将a，b与ξ分离，将关于a，b的式子进行变形，若a，b的式子化为 f ( b ) − f ( a ) b − a \frac{f(b) - f(a)}{b - a} b−af(b)−f(a)​，则用拉格朗日中值定理。若a，b的式子化为 f ( b ) − f ( a ) g ( b ) − g ( a ) \frac{f(b) - f(a)}{g(b) - g(a)} g(b)−g(a)f(b)−f(a)​，则用柯西中值定理。
• 将a，b与ξ分离，将关于ξ的式子进行变形，若ξ的式子化为φ’(x)|_x=ξ，则对φ(x)用拉格朗日中值定理。若ξ的式子化为 f ′ ( x ) g ′ ( x ) \frac{f'(x)}{g'(x)} g′(x)f′(x)​|_x=ξ，则对f(x)，g(x)使用柯西中值定理。

3.2 a，b与ξ不可分离

若ξ与a，b不可分离，一般采用凑微分法，即将结论中ξ改为x，去分母、移项，整理成g(x) = 0的形式，再找出φ’(x) = g(x)，φ(x)即为辅助函数。

四、结论中含有两个或两个以上中值的问题

4.1 结论中只含f’(ξ)，f’(η)

若待证结论中只含f’(ξ)和f’(η)，先找出函数f(x)的三个点，两次使用拉格朗日中值定理即可。

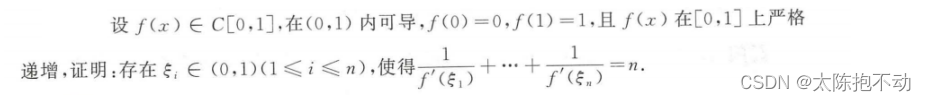
4.2 结论中含有两个中值ξ，η，但关于两个中值的项复杂度不同

这类问题通常的做法是，先将复杂中值的项取出，一般有两种情形，一种是复杂中值项为某种函数的导数，此时使用拉格朗日中值定理。另一种情形是两个函数导数之商，此时使用柯西中值定理。

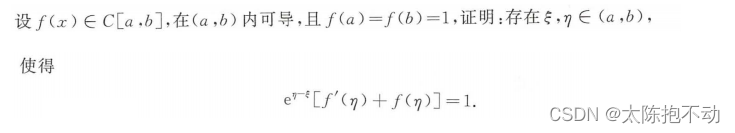
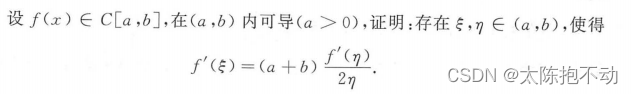
4.3 结论中含中值ξ，η（不仅仅含f’(ξ)，f’(η)），两者对应的项完全对等

该类问题一般先就ξ构造一个辅助函数（还原法），再就η构造一个辅助函数（还原法），最后再两次使用拉格朗日中值定理。

五、中值定理中关于θ的问题

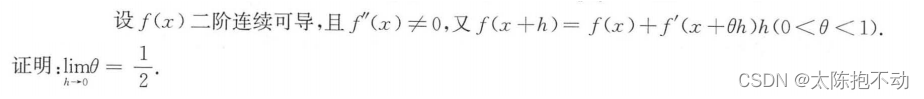
本题需要明确f(x + h)的泰勒展开式

f(x + h) = f(x) + f’(x)h + f ′ ′ ( x ) 2 ! \frac{f''(x)}{2!} 2!f′′(x)​h² + f ′ ′ ′ ( x ) 3 ! \frac{f'''(x)}{3!} 3!f′′′(x)​h³ + ……

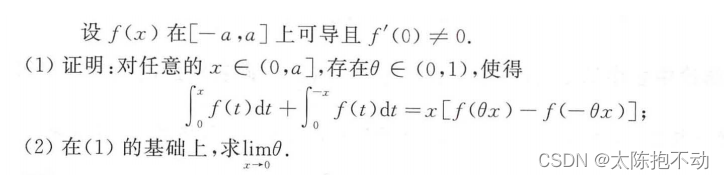
本题第一问用到了积分中值定理的推广，第二问同时除以了x²。

六、拉格朗日中值定理的两种惯性思维

若函数f(x) ∈ C[a,b]，在(a,b)内可导，以下三种情形常使用拉格朗日中值定理

• 出现f(b) - f(a)
• 出现f(a)，f ( c ) (c) (c)，f(b)
• 出现f(x)与f’(x)之间的关系式（也有可能使用牛顿莱布尼兹公式）

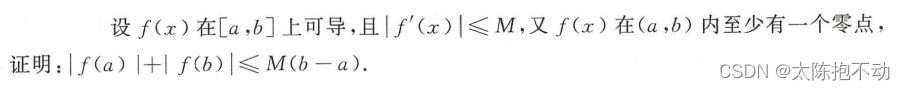
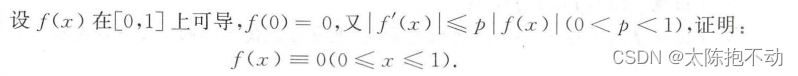
七、泰勒公式的常规证明问题

使用泰勒公式进行证明时，需要将f(x)在x₀点展开，最关键的是如何确定x₀和x，一般选取标准如下

• x₀的选取标准
  与一阶导数相关的点；区间中点
• x的选取标准
  与函数值相关的点；区间的端点

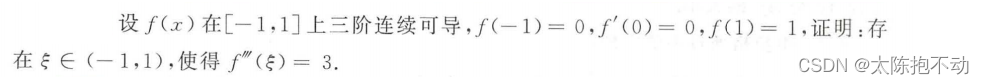
八、二阶导数保号性问题

若题中出现f’'(x) > 0（< 0）时，一般有如下两种解题思路

• 若f’‘(x) > 0（< 0），则f’(x)单调递增（单调递减）
• 若f’‘(x) > 0（< 0），则f(x) ≥ （≤）f(x₀) + f’(x₀)(x - x₀)

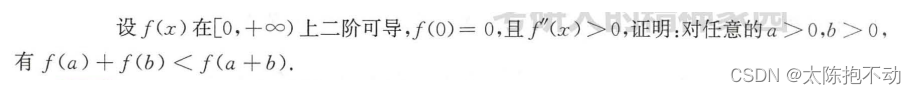
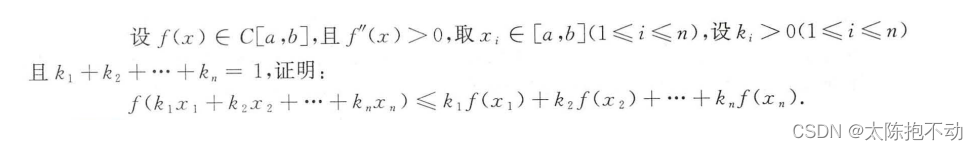
九、不等式证明

不等式证明常见的证明方法有

• 利用中值定理证明不等式
• 利用单调性证明不等式
• 利用凹凸性证明不等式
• 利用最值证明不等式

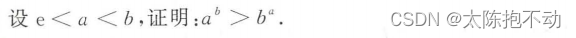
本题恒等变形后构造函数，利用单调性证明。

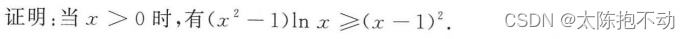
本题利用最值来证明不等式。

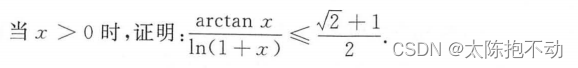
本题使用了柯西中值定理和最值来证明。

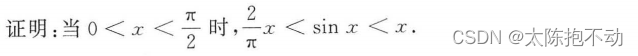
本题使用了凹凸性证明。

十、函数的零点或方程根的个数

解答函数零点或方程的根问题一般有如下三种思路

• 若f(x) ∈ C[a,b]且f(a)f(b) < 0，则使用零点定理。
• 设f(x)的原函数为F(x)，若F(a) = F(b)，则由罗尔定理，存在c ∈ (a,b)，使得F’( c c c) = 0，即f( c c c) = 0。
• 单调性方法
  第一步，给出y = f(x)（x ∈ D）。
  第二步，求f’(x) = 0的根及f(x)的不可导点，求出f(x)的极值点与极值。
  第三步，求出y = f(x)两侧的变化趋势，从而求出f(x)的零点个数。

本题使用罗尔定理证明。

十一、函数的单调性与极值、渐近线

求铅直渐近线时，讨论间断点处。

本题用到了极限的保号性。

本题最初对极限使用了洛必达法则，可以得到在x = 2处的二阶导数等于零，就认为x = 2不是f(x)的极值点，实际上一阶导与二阶导都等于零的点，也可能是极值点。