设X为离散随机变量，其全部可能取值为{a1,a2,…}，则：pi=P(X=ai)
(i=1,2,…)称为X的概率函数，也称为随机变量X的概率分布；
设X为随机变量（包括离散和非离散），则函数：P(X≤x) = F(x) (-∞ < x <∞) 称为X的分布函数；
结合概率函数和分布函数的定义，对于离散随机变量，有： P(i) = P(X=i) = F(i)-F(i-1)；
对任何随机变量X，其分布函数F(x)是单调非降的，且X->∞时，F(x)->1，X->-∞时，F(x)->0。
假设某事件A在一次试验中发生的概率为p，将该试验独立重复n次，以X记A在试验中发生的次数，X取值范围为0,1,…,n，考虑事件{X=i}出现的概率pi（表示X=i时的概率），则有：
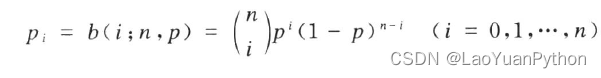
X所遵循的上述公式分布称为二项分布，常记为B(n,p)，X服从二项分布记为：X ~ B(n,p) 。之所以成为二项分布，是因为该概率与(a+b)n 的二项式展开系数相同。
重复试验n次，事件发生概率为p，发送i次，则未发生次数为n-i次，其每次的概率为1-p，由于事件发生i次时，对于不同的顺序有不同组合，因此发生i次的概率即为B(n,p)。
上述二项分布的定义中隐含了两个二项分布的条件，这也是二项分布使用的两个重要条件：
例如产品的废品率在同样的生产条件下应该是固定的，做废品率检测时，抽取的产品每次抽检后放回，则认为抽检是独立的，其概率会服从二项分布。但如果不放回，则不是独立的，因为抽检减少的数量会影响到下次抽检，如果此时抽检数量远少于产品总数，也可以近似认为是独立的，仍近似服从二项分布。
若随机变量X的可能取值为0、1、2、…，且概率分布为：P(X=i)=e-λλi/i! ，则称X服从泊松分布，常记为：X~P（λ），注意此处的λ要求为大于0的常数。
泊松分布适用于表示一定时间或空间内出现的事件个数，如一定时间范围内某交通路口的事故数。假设观察的时间段为[0,1），取一个很大的自然数n，将[0,1）等分成n段，标记为l1、l2、…，则：
l1=[0，1/n)，l2 = [1/n，2/n)，…，li = [(i-1)/n，i/n)，…，ln=[(n-1)/n，1）
做几个假定：
按照上述假定，则可以把在[0,1）内发生事故的次数X视作在n个时段内有事故的时段数，且其服从二项分布B（n，λ）。于是P(X=i) = B(n,p)=b(i;n,p)，即：
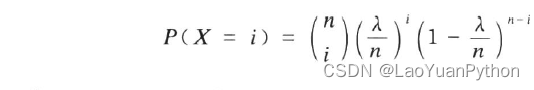
当n->∞时：
因此可以得到：P(X=i) = (
i
n
)
(
λ
n
)
i
(
1
−
λ
n
)
n
−
i
→
e
−
λ
λ
i
/
i
!
^n_i)(\frac{λ}{n})^i(1-\frac{λ}{n})^{n-i} →e^{-λ}λ^i/i!
in)(nλ)i(1−nλ)n−i→e−λλi/i!
老猿注：上图中这两个极限的值对于忘记极限知识的人来说推导还是要花点时间的，如果不清楚的请参考《由二项分布推导泊松分布中的两个使用公式的证明：https://blog.csdn.net/LaoYuanPython/article/details/127877254》。
上面已经介绍泊松分布适用于表示一定时间或空间内出现的事件个数，从上面的推导过程可以看到，泊松分布可以作为二项分布的极限得到，一般地说，如果X~B(n,p)，其中n很大，p很小，而np=λ不太大时，则X的分布接近于泊松分布P(λ)。有此基础，则可以将一些满足上面条件的二项分布转换为泊松分布去计算。
我们来看一个例子：
例 现在需要100个符合规格的元件。从市场上买的该元件有废品率0.01，故如只买100个，则它们全都符合规格的机会恐怕不大，为此我们买100+a个，a这样取，以使“在这100+a个元件中至少有100个符合规格”这个事件 A 的概率不小于0.95。问a至少要多大?
解答：
在此假定各元件是否合格是独立的，以X记在这100+a个元件中所含的废品数，则X有二项分布B(100+a，0.01)。
事件A 即事件(X≤a}于是A的概率为：
P
(
A
)
=
∑
i
=
0
a
P
（
X
=
i
）
=
∑
i
=
0
a
(
i
100
+
a
)
(
0.01
)
i
(
0.99
)
100
+
a
−
i
P(A)=\sum\limits_{i=0}^a P（X=i）=\sum\limits_{i=0}^a(^{100+a}_{\quad i})(0.01)^i(0.99)^{100+a-i}
P(A)=i=0∑aP（X=i）=i=0∑a(i100+a)(0.01)i(0.99)100+a−i
为确定最小的a使P(A)≥0.95,得从a=0开始对a=0,1,2,···依次计算上式右边的值，直到算出≥0.95的结果为止，这很麻烦。
由于100+a 这个数较大而0.01很小，(100+a)(0.01)=1+a(0.01)大小适中，可近似地用泊松分布计算。
由于平均在100个产品中只有1个废品，a谅必相当小，故可以用1近似地取代1+a(0.01)。由此X近似地服从泊松分布P(1)。
因而
P
(
X
≤
a
)
≈
∑
i
=
0
a
e
−
1
/
i
!
P(X≤a) ≈ \sum\limits_{i=0}^ae^{-1}/i!
P(X≤a)≈i=0∑ae−1/i!
计算出当a=0,1,2,3时，上式右边分别为0.368.0.736.0.920 和0.981。故取a=3已够了。
本文介绍了离散随机变量的概率函数、概率分布的定义，并介绍了两个很重要的离散随机变量的概率分布：二项分布和泊松分布，实际上泊松分布是二项分布的极限形式。
更多人工智能数学基础请参考专栏《人工智能数学基础》。
如果阅读本文于您有所获，敬请点赞、评论、收藏，谢谢大家的支持！
前两个专栏都适合有一定Python基础但无相关知识的小白读者学习，第三个专栏请大家结合《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。
对于缺乏Python基础的同仁，可以通过老猿的免费专栏《https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏：Python基础教程目录）从零开始学习Python。
如果有兴趣也愿意支持老猿的读者，欢迎购买付费专栏。
