概念
a)数据结构:是研究数据之间组织结构的一门学科。
数据结构可以理解为一组数据在计算机中的存储结构或者理解为相互之间存在一种或者多种特定关系的数据集合。
b)算法:是操作数据解决特定问题的求解步骤和方法。 一个问题可以有多种算法。
c)数据结构和算法的关系:数据结构服务于算法,算法也要作用于特定的数据结构之上,两者相辅相成,不能孤立。
d)算法五个特性:输入;输出;有穷性;确定性;可行性;
e)一个好的算法通常有四个设计要求:正确性;可读性;健壮性;高时间效率和低存储量需求;
大O时间复杂度表示法
公式T(n) = O(f(n)),其中:
a)n:表示问题规模的大小
b)T(n):表示算法的执行时间(T指的Time),也就是算法的时间复杂度。
c)f(n):表示代码的执行次数总和。
d)O:表示代码的执行时间T(n)与F(n)的函数关系(正比关系);
看几个例子(加法规则)
//1+1001+1000+1 = 2003 = 2n+3次
void calc(int n) //n=1000 问题规模
{
int sum = 0; //执行1次;
for(int i = 1; i <= n; ++i) //执行1001次
{
sum = sum + i; //执行1000次
}
cout << sum << endl; //执行1次
}
这个函数用公式表示为
T
(
n
)
=
O
(
2
n
+
3
)
=
O
(
n
)
T(n) = O(2n+3) = O(n)
T(n)=O(2n+3)=O(n)
for (int j = 1; j <= n; ++j)//执行1001次
{
for (int k = 1; k <= n; ++k) //1001 * 1000 = 1001000次
{
sum = sum + k; //1000 * 1000次 = 1000000次
}
}
用公式表示为
T
(
n
)
=
O
(
n
2
)
T(n) = O( n^2)
T(n)=O(n2)
(乘法规则)例子
int testfunc(int n) //O(n)
{
int sum = 0;
for (int i = 1; i <= n; ++i)
{
sum = sum + i;
}
return sum;
}
void cacl3(int n) //O(n * n) = O(n^2)
{
int sum = 0;
for (int i = 1; i <= n; ++i)
{
sum = sum + testfunc(i);
}
}
用公式表示为
O
(
n
∗
n
)
=
O
(
n
2
)
O(n * n) = O(n^2)
O(n∗n)=O(n2)
算法时间复杂度计算规则
加法规则:若有
T
1
(
n
)
=
O
(
f
(
n
)
)
,
T
2
(
n
)
=
O
(
g
(
n
)
)
T1(n) = O(f(n)), T2(n) = O(g(n))
T1(n)=O(f(n)),T2(n)=O(g(n)),则
T
(
n
)
=
T
1
(
n
)
+
T
2
(
n
)
=
O
(
m
a
x
(
f
(
n
)
,
g
(
n
)
)
)
T(n) = T1(n) + T2(n) = O(max(f(n),g(n)))
T(n)=T1(n)+T2(n)=O(max(f(n),g(n)))
说明:加法规则的算法时间复杂度取决于阶数最高的代码段的复杂度
乘法规则: 若有
T
1
(
n
)
=
O
(
f
(
n
)
)
,
T
2
(
n
)
=
O
(
g
(
n
)
)
T1(n) = O(f(n)), T2(n) = O(g(n))
T1(n)=O(f(n)),T2(n)=O(g(n)),则
T
(
n
)
=
T
1
(
n
)
∗
T
2
(
n
)
=
O
(
f
(
n
)
)
∗
O
(
g
(
n
)
)
=
O
(
f
(
n
)
∗
g
(
n
)
)
T(n) = T1(n) * T2(n) = O(f(n)) * O(g(n)) = O(f(n) * g(n))
T(n)=T1(n)∗T2(n)=O(f(n))∗O(g(n))=O(f(n)∗g(n))
说明:乘法规则的算法时间复杂度取决于内外循环代码段时间复杂度的乘积.
常见算法时间复杂度
O
(
1
)
O(1)
O(1):常数阶
void calc4(int n)
{
int i = 100;
int j = 15;
int sum = i + j+n;
cout << sum << endl;
}
O
(
l
o
g
2
n
)
O(log_2^n)
O(log2n):对数阶
void calc5(int n)
{
int i = 1;
while (i <= n) //2^x > n
{
i = i * 2; //i=i*3
}
}
补充:
i = i * 3的情况;
O
(
l
o
g
3
n
)
O(log_3^n)
O(log3n)
=
=
=
O
(
O(
O(
(
l
o
g
3
2
)
(log_3^2)
(log32)
×
\times
×
(
l
o
g
2
n
)
(log_2^n)
(log2n)
)
)
) =
l
o
g
2
n
log_2^n
log2n
O
(
O(
O(
n
n
n
×
\times
×
l
o
g
2
n
)
log_2^n)
log2n):线性对数阶
void calc6(int n)
{
int i = 1;
for (int count = 0; count < n; ++count)
{
while (i <= n)
{
i = i * 2; //i=i*3
}
}
}
O
(
n
2
)
O(n^2)
O(n2):平方阶
void calc8(int n)
{
int sum = 0;
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
sum++;
}
}
}
特殊情况
O
(
O(
O(
n
2
2
\frac{n^2}{2}
2n2
+
+
+
n
2
\frac{n}{2}
2n
)
)
) =
O
(
n
2
)
O(n^2)
O(n2)
结果依旧是
O
(
n
2
)
O(n^2)
O(n2)
void calc81(int n)
{
int sum = 0;
for (int i = 1; i <= n; ++i)
{
for (int j = i; j <= n; ++j) //n+(n-1)+(n-2)+....+1 -> 1+2+3+4+...+n :等差数列求和公式
{ // = n(n+1)/2 = n^2 / 2 + n / 2
sum++;
}
}
}
O
(
m
∗
n
)
O(m*n)
O(m∗n)
void calc9(int m, int n)
{
int sum = 0;
for (int i = 1; i <= m; ++i)
{
for (int j = 1; j <= n; ++j)
{
sum++;
}
}
}
O
(
m
+
n
)
O(m+n)
O(m+n)
void calc10(int m, int n)
{
int sum1 = 0;
for (int i = 1; i <= m; ++i)
{
sum1 += i;
}
int sum2 = 0;
for (int j = 1; j <= n; ++j)
{
sum2 += j;
}
}
最好、最坏、平均情况时间复杂度
最好情况时间复杂度,最坏情况时间复杂度,平均情况时间复杂度
最好情况:
O
(
1
)
O(1)
O(1)
最坏情况:
O
(
n
)
O(n)
O(n)
平均情况:
O
(
O(
O(
1
+
2
+
3
+
.
.
.
+
n
n
\frac{1+2+3+...+n}{n}
n1+2+3+...+n
)
)
)
=
=
=
O
(
O(
O(
n
+
1
2
\frac{n+1}{2}
2n+1
)
)
)
=
=
=
O
(
n
)
O(n)
O(n)
void calc11(int array[], int n, int x) //n表示元素个数
{
int pos = -1;
for (int i = 0; i < n; ++i)
{
if (array[i] == x)
{
pos = i;
break;
}
}
if (pos == -1)
cout << "没找到值为" << x << "的元素" << endl;
else
cout << "找到了值为" << x << "的元素,其在数组中的位置下标为:" <<pos << endl;
}
//调用
int asz[5] = { 1,2,3,4,5 };
calc11(asz, 5, 3);
总结
O
(
1
)
O(1)
O(1):常数阶
O
(
l
o
g
n
)
O(log^n)
O(logn):对数阶
O
(
n
)
O(n)
O(n):线性阶
O
(
n
l
o
g
n
)
O(nlog^n)
O(nlogn):线性对数阶
O
(
n
2
)
O(n^2)
O(n2):平方阶
O
(
n
3
)
O(n^3)
O(n3):立方阶。由平方阶、立方阶,扩展出k次方阶用O(n^k)表示。
O
(
2
n
)
O(2^n)
O(2n):指数阶
O
(
n
!
)
O(n!)
O(n!):阶乘阶
排序
O
(
1
)
<
O
(
l
o
g
n
)
<
O
(
n
)
<
O
(
n
l
o
g
n
)
<
O
(
n
2
)
<
O
(
n
3
)
<
O
(
2
n
)
<
O
(
n
!
)
<
O
(
n
n
)
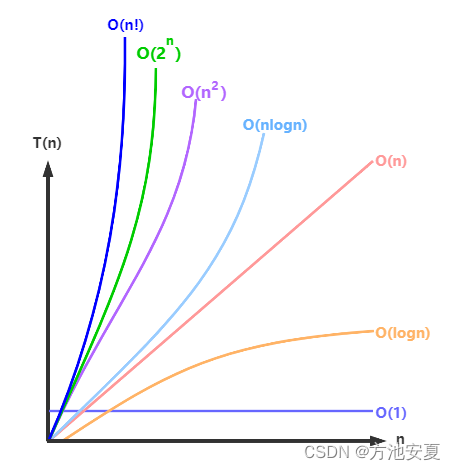
O(1) < O(log^n) < O(n) < O(nlog^n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)<O(n!)<O(nn)
空间复杂度
运行时所需要的存储空间与问题规模之间的增长关系。
a)
O
(
1
)
O(1)
O(1):常数阶空间复杂度。需要固定大小内存空间的情形也叫做算法原地工作。
//无论n如何变化,在执行过程中,所需要的空间大小都是不变的
void scalc(int n)
{
int i, sum = 0;
for (i = 1; i <= n; ++i)
{
sum = sum + 1;
}
cout << sum << endl;
}
b)
O
(
n
)
O(n)
O(n):线性阶空间复杂度。
如果每次递归调用所需要的内存空间大小固定不变,那么算法的空间复杂度一般都等于递归调用深度。
void scalc2(int n)
{
int* array = new int[n];
for (int i = 1; i <= n; ++i) //4n+4
{
array[i] = 2 * i;
}
//记得释放内存
delete[] array;
}
//递归
void scalc21(int n) //12*n = O(n)
{
int i, j;
if (n > 1)
scalc21(n - 1);
cout << "n=" << n << endl;
}
//递归的另一种情况
void scalc22(int n) //递归调用n次,n+(n-1)+(n-2)+....+1。等差数列求和公式 = n(n+1) /2 = n^2/2 + n/2
{ //O(n^2)
int* p = new int[n];
if (n > 1)
scalc21(n - 1);
cout << "n=" << n << endl;
delete[]p;
}
注意:scalc22的空间复杂度为
O
(
n
2
)
O(n^2)
O(n2)
c)
O
(
n
2
)
O(n^2)
O(n2):平方阶空间复杂度表示法
void scalc3(int n) //空间复杂度O(n^2)
{
//注意这里的动态二维数组的初始化代码
int** array;
array = new int* [n]; //4n
for (int i = 0; i < n; ++i)
array[i] = new int[n]; //每执行一次占用4n个字节。一共占用的是4n*n = 4n^2个字节的内存
//注意动态二维数组的内存释放代码
for (int i = 0; i < n; i++)
{
delete[] array[i];
}
delete[] array;
}