上一章我们介绍了潜在结果模型,这一章我们尝试从图的角度理解因果,大家都有图论基础,我就不多赘述图的基本概念了,在因果图里我们主要研究DAG(directed acyclic graph,有向无环图),如图1。
 图1. 一个DAG例子
图1. 一个DAG例子
Bayesian Networks
贝叶斯网络,一个概率图模型,因果图就是由此内生而来,因此先介绍它,贝叶斯网络的职责是将概率和图模型结合起来,使得我们能直接利用图表示概率关系,而想用图模型来表示概率关系,需要先提出两个假设。
首先,我们从概率建模出发,如果我们相对一组数据的分布
P
(
x
1
,
x
2
,
.
.
.
,
x
n
)
P(x_1,x_2,...,x_n)
P(x1,x2,...,xn)建模,则根据条件概率的链式法则,我们可以将该分布分解为:
P
(
x
1
,
x
2
,
.
.
.
,
x
n
)
=
P
(
x
1
)
∏
i
P
(
x
i
∣
x
i
−
1
,
.
.
.
,
x
1
)
P(x_1,x_2,...,x_n)=P(x_1)\prod_iP(x_i|x_{i-1},...,x_1)
P(x1,x2,...,xn)=P(x1)∏iP(xi∣xi−1,...,x1)
而如果给定图1,我们想求图1中的分布关系,我们就需要先定义图1对应的分布情况。
因此先提出一个最基础的假设:DAG中相邻的点是依赖关系。
利用这个假设,可以推出
P
(
x
1
,
x
2
,
x
3
,
x
4
)
=
P
(
x
1
)
P
(
x
2
∣
x
1
)
P
(
x
3
∣
x
2
,
x
1
)
P
(
x
4
∣
x
3
,
x
2
,
x
1
)
P(x_1,x_2,x_3,x_4)=P(x_1)P(x_2|x_1)P(x_3|x_2,x_1)P(x_4|x_3,x_2,x_1)
P(x1,x2,x3,x4)=P(x1)P(x2∣x1)P(x3∣x2,x1)P(x4∣x3,x2,x1)。但大家还记得概率论的话就会知道,这样没加一个变量,参数就会指数级上升,如图2所示。因此光是一个依赖假设还是不够,我们需要引入独立假设,减少不必要的计算量。
 图2. 链式法则求解
图2. 链式法则求解
Local Markov assumption
局部马尔科夫假设。
为了避免指数爆炸的情况,我们想如果能让每个节点只依赖于其父节点就好了,这就是局部马尔科夫假设:给定一个DAG图,点X独立于其所有的非子孙节点。
再基于该假设,我们可以进一步将图1的概率分布分解为
P
(
x
1
,
x
2
,
x
3
,
x
4
)
=
P
(
x
1
)
P
(
x
2
∣
x
1
)
P
(
x
3
∣
x
2
,
x
1
)
P
(
x
4
∣
x
3
)
P(x_1,x_2,x_3,x_4)=P(x_1)P(x_2|x_1)P(x_3|x_2,x_1)P(x_4|x_3)
P(x1,x2,x3,x4)=P(x1)P(x2∣x1)P(x3∣x2,x1)P(x4∣x3),我们称之为Bayesian network factorization(贝叶斯网络分解),即给定一个概率分布P和DAG G,如果
P
(
x
1
,
.
.
.
x
n
)
=
∏
i
P
(
x
i
∣
p
a
i
)
P(x_1,...x_n)=\prod_iP(x_i|pa_i)
P(x1,...xn)=∏iP(xi∣pai),则P可以根据G进行分解,局部马尔科夫假设是这种贝叶斯网络分解形式的充要条件。
Minimality assumption
整合Local Markov assumption和”依赖“假设,我们便得到了极小假设:
-
给定一个DAG图,点X独立于其所有的非子孙节点。
-
DAG中相邻的点是依赖关系
我们称关于G且满足极小假设的P是马尔科夫的。
这就是贝叶斯网络的假设,下面我们看看因果图模型。
Causal graph
因果图。
首先,定义因果关系:如果变量Y响应于变量X的变化,则X是变量Y的因。
根据这个定义,因果图的第一个假设,Causal Edges Assumption(因果边假设):在一个有向图中,每一个父亲节点都是孩子节点的因。
这样因果图就基于两个假设:
- Minimality assumption
- Causal Edges Assumption
仅仅知道这两个假设理论上就可以求出所有的因果关系,但在实践中,当因果关系复杂起来就很难分析,因此我们需要总结一些基本的block。
两个节点之间的关系
图3是只考虑两个节点时的所有关系情况,(a)表示
x
1
x_1
x1和
x
2
x_2
x2没有边,其表示的概率关系为
P
(
x
1
,
x
2
)
=
P
(
x
1
)
P
(
x
2
)
P(x_1, x_2)=P(x_1)P(x_2)
P(x1,x2)=P(x1)P(x2),
x
1
x_1
x1和
x
1
x_1
x1相互独立(Local Markov assumption);(b)表示
x
1
x_1
x1和
x
2
x_2
x2之间有因果关系,
x
1
x_1
x1是
x
2
x_2
x2的因(Causal Edges Assumption),证明如下,我们对a和b的概率图进行贝叶斯分解得到:
(a):
P
(
x
1
,
x
2
)
=
P
(
x
1
)
P
(
x
2
)
P(x_1, x_2)=P(x_1)P(x_2)
P(x1,x2)=P(x1)P(x2)
(b):
P
(
x
1
,
x
2
)
=
P
(
x
1
)
P
(
x
2
∣
x
1
)
P(x_1,x_2)=P(x_1)P(x_2|x_1)
P(x1,x2)=P(x1)P(x2∣x1)
 图3. 两节点的关系
图3. 两节点的关系
只有两个点的关系还是很好理解的,下面让我们看看三个点的关系。
三个节点之间的关系
如图4,当考虑三个节点时共有三种情况,我们首先分析chain和fork。
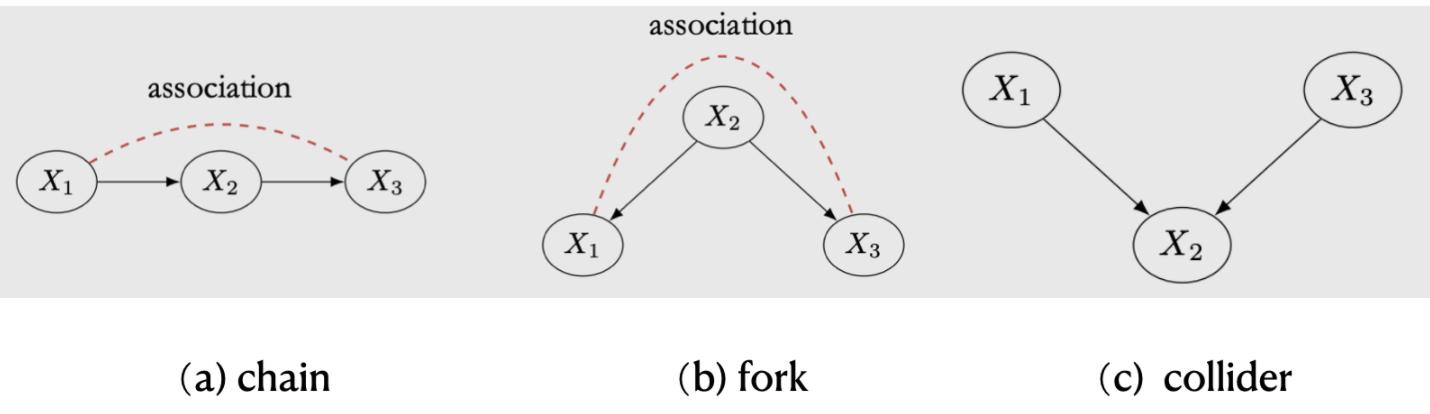 图4. 三节点的关系
图4. 三节点的关系
chains and forks
chains( 链式结构)和 forks (分叉结构)拥有相同的依赖关系(第10章会详细讨论),其依赖关系的传递如图4红线所示。
当我们同时condition on x2, chains 和 forks 还拥有相同的独立关系,x1和x3的关联被x2 blocked(阻断了),即
x
1
⊥
⊥
x
3
∣
x
2
x_1 {\perp \!\!\! \perp} x_3|x_2
x1⊥⊥x3∣x2,如图5所示。
 图5. x2条件下的chain和fork
图5. x2条件下的chain和fork
从概率角度分析,chain图得到:
P
(
x
1
,
x
2
,
x
3
)
=
P
(
x
1
)
P
(
x
2
∣
x
1
)
P
(
x
3
∣
x
2
)
P(x_1,x_2,x_3)=P(x_1)P(x_2|x_1)P(x_3|x_2)
P(x1,x2,x3)=P(x1)P(x2∣x1)P(x3∣x2)(Bayesian network factorization),
两边同时除以
P
(
x
2
)
P(x_2)
P(x2):
P
(
x
1
,
x
2
,
x
3
)
P
(
x
2
)
=
P
(
x
1
)
P
(
x
2
∣
x
1
)
P
(
x
3
∣
x
2
)
P
(
x
2
)
\frac{P(x_1,x_2,x_3)}{P(x_2)}=\frac{P(x_1)P(x_2|x_1)P(x_3|x_2)}{P(x_2)}
P(x2)P(x1,x2,x3)=P(x2)P(x1)P(x2∣x1)P(x3∣x2)
P
(
x
1
,
x
3
∣
x
2
)
=
P
(
x
1
)
P
(
x
2
,
x
1
)
P
(
x
3
∣
x
2
)
P
(
x
2
)
P
(
x
1
)
=
P
(
x
2
,
x
1
)
P
(
x
3
∣
x
2
)
P
(
x
2
)
=
P
(
x
1
∣
x
2
)
P
(
x
3
∣
x
2
)
P(x_1,x_3|x_2)=\frac{P(x_1)P(x_2,x_1)P(x_3|x_2)}{P(x_2)P(x_1)}=\frac{P(x_2,x_1)P(x_3|x_2)}{P(x_2)}=P(x_1|x_2)P(x_3|x_2)
P(x1,x3∣x2)=P(x2)P(x1)P(x1)P(x2,x1)P(x3∣x2)=P(x2)P(x2,x1)P(x3∣x2)=P(x1∣x2)P(x3∣x2),即
x
2
x_2
x2条件下,
x
1
x_1
x1条件独立于
x
3
x_3
x3。
fork图得到
P
(
x
1
,
x
2
,
x
3
)
=
P
(
x
2
)
P
(
x
1
∣
x
2
)
P
(
x
3
∣
x
2
)
P(x_1,x_2,x_3)=P(x_2)P(x_1|x_2)P(x_3|x_2)
P(x1,x2,x3)=P(x2)P(x1∣x2)P(x3∣x2)(Bayesian network factorization)
两边同时除以
P
(
x
2
)
P(x_2)
P(x2):
P
(
x
1
,
x
2
,
x
3
)
P
(
x
2
)
=
P
(
x
2
)
P
(
x
1
∣
x
2
)
P
(
x
3
∣
x
2
)
P
(
x
2
)
\frac{P(x_1,x_2,x_3)}{P(x_2)}=\frac{P(x_2)P(x_1|x_2)P(x_3|x_2)}{P(x_2)}
P(x2)P(x1,x2,x3)=P(x2)P(x2)P(x1∣x2)P(x3∣x2)
P
(
x
1
,
x
3
∣
x
2
)
=
P
(
x
1
∣
x
2
)
P
(
x
3
∣
x
2
)
P(x_1,x_3|x_2)=P(x_1|x_2)P(x_3|x_2)
P(x1,x3∣x2)=P(x1∣x2)P(x3∣x2),即
x
2
x_2
x2条件下,
x
1
x_1
x1条件独立于
x
3
x_3
x3。
collider
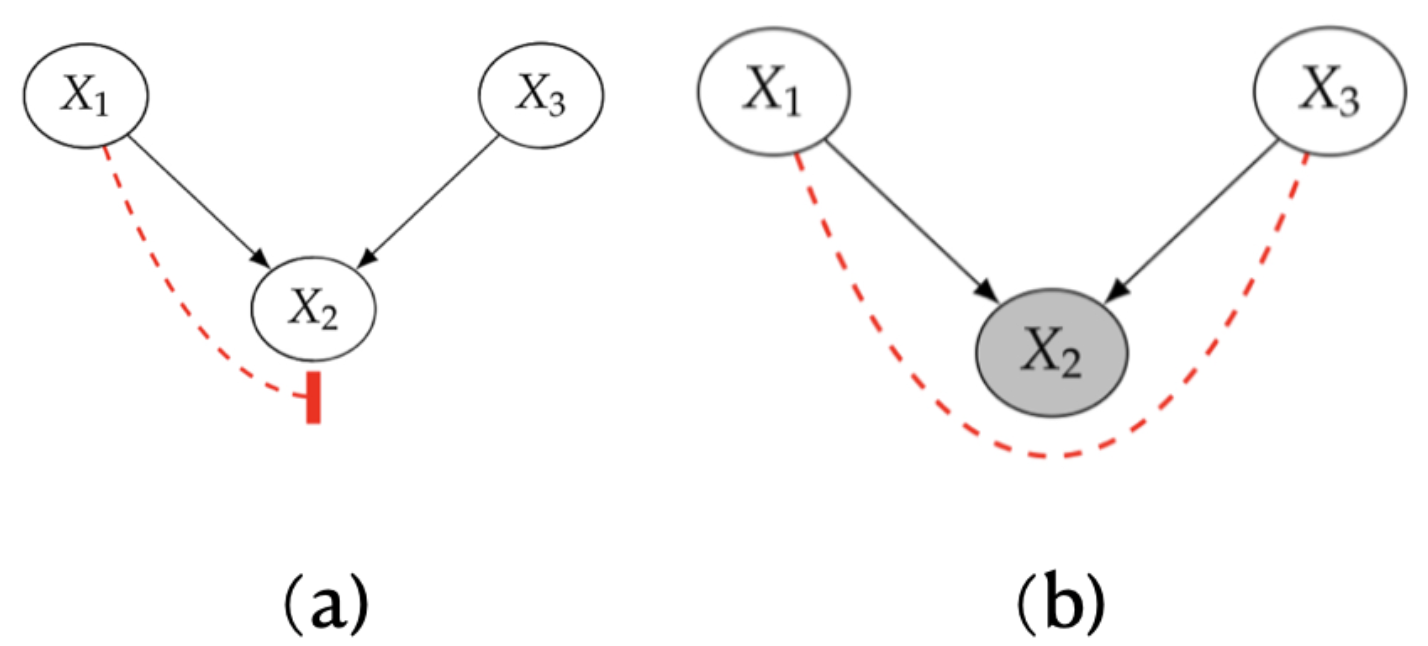 图6. collider的两种情况
图6. collider的两种情况
如图6a,collider(对撞结构)与前两种结构不同,collider中x1和x3没有关联关系,x1和x3的关联被x2 blocked了,证明如下:
P
(
x
1
,
x
3
)
=
∑
x
2
P
(
x
1
,
x
2
,
x
3
)
=
∑
x
2
P
(
x
1
)
P
(
x
3
)
P
(
x
2
∣
x
1
,
x
3
)
=
P
(
x
1
)
P
(
x
3
)
∑
x
2
P
(
x
2
∣
x
1
,
x
3
)
=
P
(
x
1
)
P
(
x
3
)
P(x_1,x_3)=\sum_{x_2}P(x_1,x_2,x_3)=\sum_{x_2}P(x_1)P(x_3)P(x_2|x_1,x_3)=P(x_1)P(x_3)\sum_{x_2}P(x_2|x_1,x_3)=P(x_1)P(x_3)
P(x1,x3)=∑x2P(x1,x2,x3)=∑x2P(x1)P(x3)P(x2∣x1,x3)=P(x1)P(x3)∑x2P(x2∣x1,x3)=P(x1)P(x3)
如图6b,而当在x2条件下时,x1和x3反而建立起一种虚假的关联,x1和x3的关联被x2unblocked,证明:
P
(
x
1
,
x
2
,
x
3
)
=
P
(
x
1
)
P
(
x
3
)
P
(
x
2
∣
x
1
,
x
3
)
P(x_1,x_2,x_3)=P(x_1)P(x_3)P(x_2|x_1,x_3)
P(x1,x2,x3)=P(x1)P(x3)P(x2∣x1,x3)(Bayesian network factorization),
两边同时除以
P
(
x
2
)
P(x_2)
P(x2):
P
(
x
1
,
x
3
∣
x
2
)
=
P
(
x
1
)
P
(
x
3
)
P
(
x
2
∣
x
1
,
x
3
)
P
(
x
2
)
P(x_1,x_3|x_2)=P(x_1)P(x_3)\frac{P(x_2|x_1,x_3)}{P(x_2)}
P(x1,x3∣x2)=P(x1)P(x3)P(x2)P(x2∣x1,x3),可见在x2条件下,x1与x3不满足条件独立。
最后我们还可以根据collider的性质延伸出一种情况,如图7所示,如果我们condition on x2的子孙,也会产生虚假的关联,这个关联流向为x4->x2->(x1,x3)。
 图7. collider的子孙
图7. collider的子孙
D-separation
现在我们对上面谈到的情况对点之间的关系进行总结,将几个点之间的关系拓展到整个图。
首先我们正式定义blocked概念。对于单条路径,如果:
- 路径中存在chain …->W->…或者fork…<-W->…结构,
W
∈
Z
W\in Z
W∈Z
- 路径中存在collider …->W<-…,
W
∉
Z
W \notin Z
W∈/Z且W的子孙
d
e
(
W
)
∉
Z
de(W)\notin Z
de(W)∈/Z
则称X和Y之间的这条路径被条件集Z blocked(阻断),条件集Z可以是空集。与之相对,unblocked路径便是不满足blocked条件的路径。
然后基于blocked,我们定义d-separation,如果:
两个顶点集合X和Y之间的路径全部被Z blocked,则称X和Y被Z d-separation。 如果二者之间存在unblocked路径,则称X和Y是d-connected。
再扩展到整个图的关系,首先我们定义一些符号:如果在Z条件下,X和Y在图G中是d-separation的,则
X
⊥
⊥
G
Y
∣
Z
X {\perp \!\!\! \perp}_G Y|Z
X⊥⊥GY∣Z;如果在Z条件下,X和Y在分布P中是条件独立的,则
X
⊥
⊥
P
Y
∣
Z
X {\perp \!\!\! \perp}_P Y|Z
X⊥⊥PY∣Z。
有了这些符号,我们定义global Markov assumption:
给定P关于G是马尔科夫的(满足local Markov assumption),如果在Z条件下,X和Y在G中是 d-separation 的,则在Z条件下,X和Y在分布P中是条件独立的,即:
X
⊥
⊥
G
Y
∣
Z
=
>
X
⊥
⊥
P
Y
∣
Z
X {\perp \!\!\! \perp}_G Y|Z =>X {\perp \!\!\! \perp}_P Y|Z
X⊥⊥GY∣Z=>X⊥⊥PY∣Z
local Markov assumption,global Markov assumption 和 Bayesian network factorization是不同角度的理解,他们三者是完全等价的,可以将这三者统称为Markov assumption,或者说P关于G是马尔科夫的。
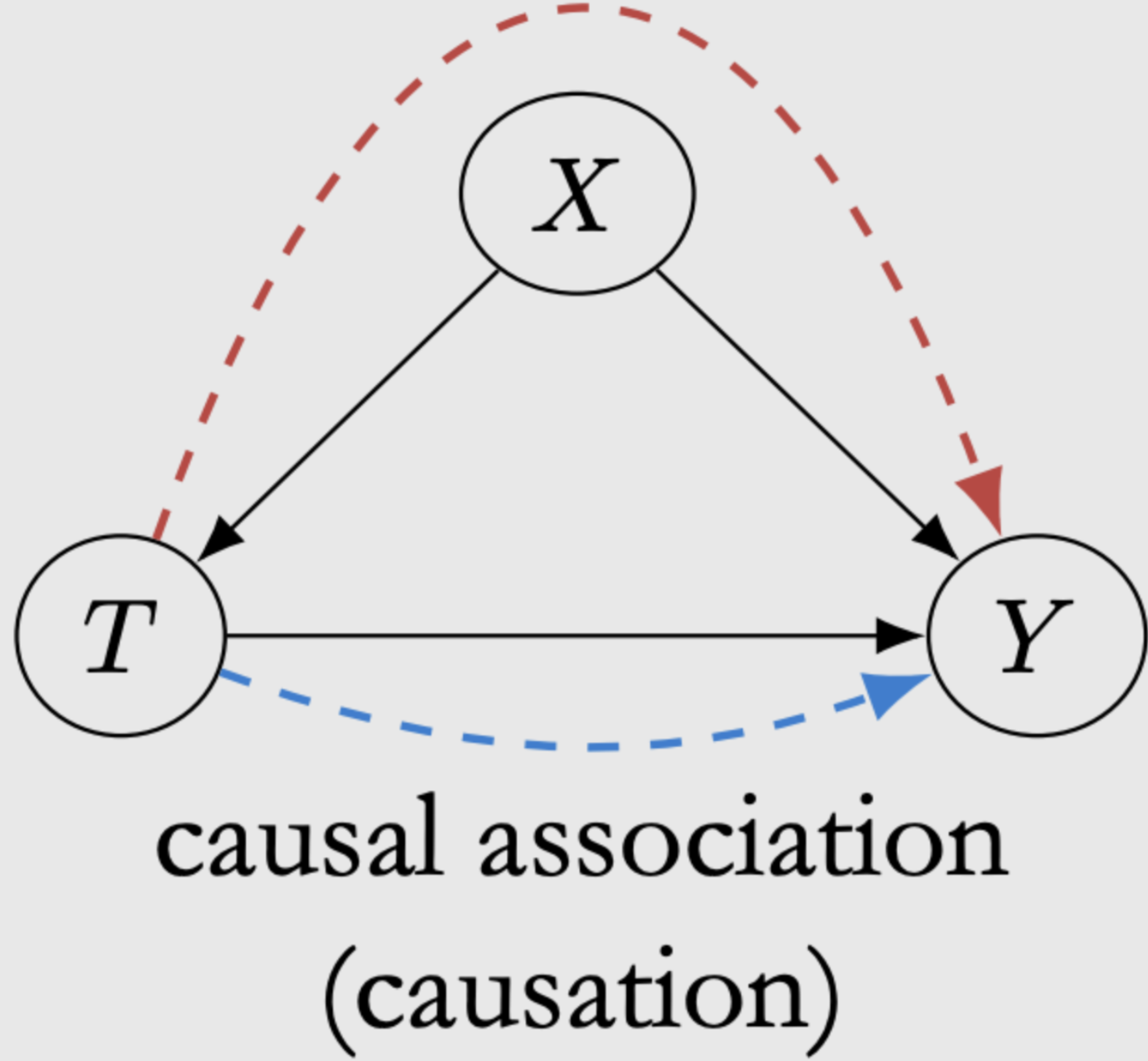 图8. 因果关联
图8. 因果关联
这一章我们详细探讨了因果图中点与点之间关系,并学习了如何分辨关系以及使其独立的方法。但在因果推理中,我们希望得到的是因果关系,而不是独立关系,这需要一些方法能够抛开非因果关联,只留下因果关联,如图8所示,只考虑蓝色线。然后计算因果效应。后面我们会进一步学习因果模型,看他是如何解决这些问题的。
Reference
Introduction to Causal Inference