Grant: 普适的代价是抽象。
仔细分析就会发现,关于向量空间的一切概念及有关定理都不依赖于向量的具体表现形式(有序数组),也不依赖于向量加法、数乘的具体计算式,而只依赖于如下两点:
这一事实告诉我们:可以把向量的有序数组这一具体表达形式及加法、数乘的具体计算式这些非本质的东西拋弃 ,只把最根本的八条运算法则保留下来。这时它们就不能从理论上给予证明,而要当作公理加以承认。这样,我们就形成了本章的核心概念,也是线性代数这门学科的基本研究对象:数域上的抽象线性空间。
接下来,把向量空间的概念从理论上加以概括和抽象,就得到线性空间的一般性概念,它具有更大的普遍性,应用范围也更广。
线性空间:设 V V V 是非空集合, F \mathbb F F 是一个数域。对 V V V 中的元素定义两种运算:加法 v + w ( v , w ∈ V ) \mathbf v+\mathbf w\quad (\mathbf v,\mathbf w\in V) v+w(v,w∈V) 和数乘 c v ( c ∈ F , v ∈ V ) c\mathbf v\quad(c\in\mathbb F,\mathbf v\in V) cv(c∈F,v∈V) 。若 V V V 对于加法和数乘运算封闭:
且 ∀ u , v , w ∈ V \forall\mathbf u,\mathbf v,\mathbf w\in V ∀u,v,w∈V and ∀ a , b ∈ F \forall a,b\in\mathbb F ∀a,b∈F 满足以下8条性质:
则称集合 V V V 为数域 F \mathbb F F 上的线性空间(或向量空间)。线性空间中的元素统称为向量,线性空间中的加法和数乘运算称为线性运算。
注意:
- 线性空间的概念是集合与运算二者的结合。同一个集合,若定义两种不同的线性运算,就构成不同的线性空间。
- 线性空间中的向量不一定是有序数组。它已不再具有三维几何空间中向量的几何直观意义。
- 线性运算不一定是有序数组的加法及数乘运算。
然后,之前向量空间的一切结论和性质都可同步到线性空间。
例 1:实数域上次数不大于
m
m
m 的全体多项式构成线性空间,记为
P
m
(
R
)
=
{
f
(
x
)
=
a
0
+
a
1
x
+
⋯
+
a
m
x
m
∣
a
0
,
⋯
,
a
m
∈
R
}
P_m(\R)=\{f(x)=a_0+a_1x+\cdots+a_mx^m\mid a_0,\cdots,a_m\in\R\}
Pm(R)={f(x)=a0+a1x+⋯+amxm∣a0,⋯,am∈R}。
例 2:全体
m
×
n
m×n
m×n 实矩阵构成线性空间,记为
R
m
×
n
\R^{m\times n}
Rm×n。
例 3:全体函数的集合构成线性空间,也称函数空间。
性质:
子空间:设 U U U 是向量空间 V V V 的一个非空子集,如果 U U U中的线性运算封闭,则 U U U 也是向量空间,称为 V V V 的子空间。
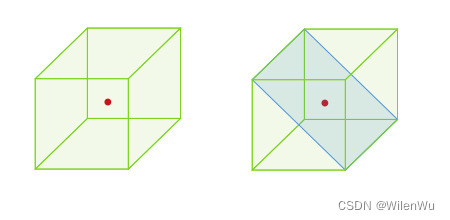
子空间的和:设
U
1
,
U
2
U_1,U_2
U1,U2 为线性空间
V
V
V 的两个子空间,则
U
1
+
U
2
=
{
u
1
+
u
2
∣
u
1
∈
U
1
,
u
2
∈
U
2
}
U_1+U_2=\{\mathbf u_1+\mathbf u_2\mid \mathbf u_1\in U_1,\mathbf u_2\in U_2\}
U1+U2={u1+u2∣u1∈U1,u2∈U2}
称为子空间
U
1
,
U
2
U_1,U_2
U1,U2 的和(sum of subspaces) 。两个子空间的和是分别由两个子空间中各任取一个向量相加所组成的集合。注意
U
1
+
U
2
U_1+U_2
U1+U2 和
U
1
∪
U
2
U_1\cup U_2
U1∪U2 不同,后者只是把两个子空间的向量简单地聚拢在一起,成为一个新的集合而已,它们的向量之间并不相加,在一般情况下,
U
1
∪
U
2
≠
U
1
+
U
2
U_1\cup U_2\neq U_1+U_2
U1∪U2=U1+U2 。
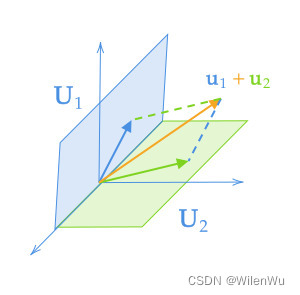
U 1 + U 2 U_1+U_2 U1+U2 是包含子空间 U 1 , U 2 U_1,U_2 U1,U2 的最小子空间。
设
U
1
=
span
{
a
1
,
⋯
,
a
p
}
,
U
2
=
span
{
b
1
,
⋯
,
b
q
}
U_1=\text{span}\{\mathbf a_1,\cdots,\mathbf a_p\},\quad U_2=\text{span}\{\mathbf b_1,\cdots,\mathbf b_q\}
U1=span{a1,⋯,ap},U2=span{b1,⋯,bq} 则
U
1
+
U
2
=
span
{
a
1
,
⋯
,
a
p
,
b
1
,
⋯
,
b
q
}
U_1+U_2=\text{span}\{\mathbf a_1,\cdots,\mathbf a_p,\mathbf b_1,\cdots,\mathbf b_q\}
U1+U2=span{a1,⋯,ap,b1,⋯,bq}
维数公式:
dim
(
U
1
+
U
2
)
=
dim
U
1
+
dim
U
2
−
dim
(
U
1
∩
U
2
)
\dim(U_1+U_2)=\dim U_1+\dim U_2-\dim(U_1\cap U_2)
dim(U1+U2)=dimU1+dimU2−dim(U1∩U2)
直和:若任意向量
u
∈
U
1
+
U
2
\mathbf u\in U_1+U_2
u∈U1+U2 能唯一的表示成
u
=
u
1
+
u
1
(
u
1
∈
U
1
,
u
2
∈
U
2
)
\mathbf u=\mathbf u_1+\mathbf u_1\quad (\mathbf u_1\in U_1,\mathbf u_2\in U_2)
u=u1+u1(u1∈U1,u2∈U2)
则称子空间
U
1
+
U
2
U_1+U_2
U1+U2 为直和(direct sum),记作
U
1
⊕
U
2
U_1\oplus U_2
U1⊕U2 。
U 1 + U 2 U_1+U_2 U1+U2 是直和 ⟺ \iff ⟺ U 1 ∩ U 2 = { O } U_1\cap U_2=\{O\} U1∩U2={O}
类似之前向量空间讨论过的,确定线性空间
V
V
V 的一组基后,对于任一向量
v
∈
V
\mathbf v\in V
v∈V 可唯一线性表示为
v
=
x
1
a
1
+
x
2
a
2
+
⋯
+
x
n
a
n
\mathbf v=x_1\mathbf a_1+x_2\mathbf a_2+\cdots+x_n\mathbf a_n
v=x1a1+x2a2+⋯+xnan
向量的坐标为
[
x
1
x
2
⋮
x
n
]
or
(
x
1
,
x
2
,
⋯
,
x
n
)
\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}\quad \text{or}\quad (x_1,x_2,\cdots,x_n)
x1x2⋮xn
or(x1,x2,⋯,xn)
建立了坐标之后, n n n维线性空间 V n V_n Vn 中的抽象元素与 n n n 维向量空间 R n \R^n Rn 中的具体数组之间就有一一对应的关系,并且保持了线性组合(线性运算)的一一对应。
设 v ↔ ( v 1 , v 2 , ⋯ , v n ) T , w ↔ ( w 1 , w 2 , ⋯ , w n ) T \mathbf v\lrarr (v_1,v_2,\cdots,v_n)^T,\quad \mathbf w\lrarr (w_1,w_2,\cdots,w_n)^T v↔(v1,v2,⋯,vn)T,w↔(w1,w2,⋯,wn)T,则
因此可以说 V n V_n Vn 与 R n \R^n Rn 有相同的结构。
一般地,设 V V V 与 U U U 是两个线性空间,如果在它们的元素之间有一一对应关系,且这个对应关系保持线性组合的对应,那么就说线性空间 V V V 与 U U U 同构(isomorphism)。
显然,任何实数域上的 n n n维线性空间都与 R n \R^n Rn 同构,即维数相同的线性空间都同构,从而可知,线性空间的结构完全被它的维数所决定。
同构的概念除元素一一对应外,主要是保持线性运算的对应关系。因此, V n V_n Vn 中的抽象的线性运算就可转化为 R n \R^n Rn 中的线性运算,并且 R n \R^n Rn 中凡是涉及线性运算的性质就都适用于 V n V_n Vn 。
变换(transformation)是线性空间的一种映射
T
:
v
↦
T
(
v
)
T:\quad \mathbf v\mapsto T(\mathbf v)
T:v↦T(v)
称
T
(
v
)
T(\mathbf v)
T(v) 为向量
v
\mathbf v
v 在映射
T
T
T 下的像,而称
v
\mathbf v
v 为
T
(
v
)
T(\mathbf v)
T(v) 在映射
T
T
T 下的原像。
满足下列两条性质的变换称为线性变换(linear transformation)
设
V
V
V 是数域
R
\R
R 上的
n
n
n 维线性空间,
e
1
,
e
2
,
⋯
,
e
n
\mathbf e_1,\mathbf e_2,\cdots,\mathbf e_n
e1,e2,⋯,en 是
V
V
V 的一组基。基向量
e
j
\mathbf e_j
ej 是单位阵
I
j
I_j
Ij 的第
j
j
j 列。对于任一向量
v
∈
V
\mathbf v\in V
v∈V ,设
v
=
[
x
1
x
2
⋮
x
n
]
=
x
1
e
1
+
x
2
e
2
+
⋯
+
x
n
e
n
\mathbf v=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}=x_1\mathbf e_1+x_2\mathbf e_2+\cdots+x_n\mathbf e_n
v=
x1x2⋮xn
=x1e1+x2e2+⋯+xnen
对于线性变换
T
T
T,由线性变换的基本性质知
T
(
v
)
=
T
(
x
1
e
1
+
x
2
e
2
+
⋯
+
x
n
e
n
)
=
x
1
T
(
e
1
)
+
x
2
T
(
e
2
)
+
⋯
+
x
n
T
(
e
n
)
=
[
T
(
e
1
)
T
(
e
2
)
⋯
T
(
e
n
)
]
[
x
1
x
2
⋮
x
n
]
=
A
v
\begin{aligned} T(\mathbf v)&=T(x_1\mathbf e_1+x_2\mathbf e_2+\cdots+x_n\mathbf e_n) =x_1T(\mathbf e_1)+x_2T(\mathbf e_2)+\cdots+x_nT(\mathbf e_n) \\ &=\begin{bmatrix}T(\mathbf e_1)&T(\mathbf e_2)&\cdots&T(\mathbf e_n)\end{bmatrix}\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix} =A\mathbf v \end{aligned}
T(v)=T(x1e1+x2e2+⋯+xnen)=x1T(e1)+x2T(e2)+⋯+xnT(en)=[T(e1)T(e2)⋯T(en)]
x1x2⋮xn
=Av
矩阵
A
A
A 称为线性变换
T
T
T 在基
e
1
,
e
2
,
⋯
,
e
n
\mathbf e_1,\mathbf e_2,\cdots,\mathbf e_n
e1,e2,⋯,en 下的矩阵。其中,矩阵
A
A
A 的第
j
j
j 列是基向量
e
j
\mathbf e_j
ej 的像
T
(
e
j
)
T(\mathbf e_j)
T(ej)。显然,矩阵
A
A
A 由基的像唯一确定。
示例:函数是一种特殊的线性空间,定义一个映射:
D
=
d
d
x
:
f
(
x
)
↦
f
′
(
x
)
D=\frac{\mathrm d}{\mathrm dx}:\quad f(x)\mapsto f'(x)
D=dxd:f(x)↦f′(x)
由导数的性质可知,
D
D
D 是函数空间中的一个线性变换,称为微分变换。
在多项式空间
R
[
x
]
n
\R[x]_n
R[x]n 内,对任一多项式
f
(
x
)
=
a
0
+
a
1
x
1
+
a
2
x
2
+
⋯
+
a
n
x
n
f(x)=a_0+a_1x_1+a_2x^2+\cdots+a_nx^n
f(x)=a0+a1x1+a2x2+⋯+anxn
在基
1
,
x
,
x
2
,
⋯
,
x
n
1,x,x^2,\cdots,x^n
1,x,x2,⋯,xn 下的坐标表达式为
f
(
x
)
=
(
1
,
x
,
x
2
,
⋯
,
x
n
)
[
a
0
a
1
a
2
⋮
a
n
]
f(x)=(1,x,x^2,\cdots,x^n)\begin{bmatrix}a_0\\a_1\\a_2\\\vdots\\a_n\end{bmatrix}
f(x)=(1,x,x2,⋯,xn)
a0a1a2⋮an
基向量
1
,
x
,
x
2
,
⋯
,
x
n
1,x,x^2,\cdots,x^n
1,x,x2,⋯,xn 的线性变换
D
1
=
0
,
D
x
=
1
,
D
x
2
=
2
x
,
⋯
D
x
n
=
n
x
n
−
1
\begin{aligned}&D1=0,\\&D x=1,\\&Dx^2=2x,\\&\cdots\\&Dx^n=nx^{n-1}\end{aligned}
D1=0,Dx=1,Dx2=2x,⋯Dxn=nxn−1
故
D
D
D 在基
1
,
x
,
x
2
,
⋯
,
x
n
1,x,x^2,\cdots,x^n
1,x,x2,⋯,xn 下的矩阵为
D
=
[
0
1
0
⋯
0
0
0
2
⋯
0
⋮
⋮
⋮
⋱
⋮
0
0
0
⋯
n
0
0
0
⋯
0
]
D=\begin{bmatrix} 0&1&0&\cdots&0\\ 0&0&2&\cdots&0\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\cdots&n\\ 0&0&0&\cdots&0\end{bmatrix}
D=
00⋮0010⋮0002⋮00⋯⋯⋱⋯⋯00⋮n0
D
f
(
x
)
Df(x)
Df(x) 在基
1
,
x
,
x
2
,
⋯
,
x
n
1,x,x^2,\cdots,x^n
1,x,x2,⋯,xn 下的坐标为
D
f
(
x
)
=
[
0
1
0
⋯
0
0
0
2
⋯
0
⋮
⋮
⋮
⋱
⋮
0
0
0
⋯
n
0
0
0
⋯
0
]
[
a
0
a
1
a
2
⋮
a
n
]
=
[
a
1
2
a
2
3
a
3
⋮
0
]
Df(x)=\begin{bmatrix} 0&1&0&\cdots&0\\ 0&0&2&\cdots&0\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 0&0&0&\cdots&n\\ 0&0&0&\cdots&0\end{bmatrix} \begin{bmatrix}a_0\\a_1\\a_2\\\vdots\\a_n\end{bmatrix}= \begin{bmatrix}a_1\\2a_2\\3a_3\\\vdots\\0\end{bmatrix}
Df(x)=
00⋮0010⋮0002⋮00⋯⋯⋱⋯⋯00⋮n0
a0a1a2⋮an
=
a12a23a3⋮0
即
D
f
(
x
)
=
a
1
+
2
a
2
x
+
3
a
3
x
2
+
⋯
+
n
a
n
x
n
−
1
Df(x)=a_1+2a_2x+3a_3x^2+\cdots+na_nx^{n-1}
Df(x)=a1+2a2x+3a3x2+⋯+nanxn−1,和直接求导的形式一致。
Grant:坐标系的建立基于所选的基向量
以二维空间为例,Grant 选用标准坐标系下的基向量,坐标值为
i
=
[
1
0
]
,
j
=
[
0
1
]
\mathbf i=\begin{bmatrix} 1 \\ 0 \end{bmatrix},\quad \mathbf j=\begin{bmatrix} 0 \\ 1 \end{bmatrix}
i=[10],j=[01]
而 Jennifer 使用另外一组基向量
i
′
,
j
′
\mathbf i',\mathbf j'
i′,j′,在 Grant 的坐标系下的坐标表示为
i
′
=
[
a
c
]
,
j
′
=
[
b
d
]
\mathbf i'=\begin{bmatrix} a \\ c \end{bmatrix},\quad \mathbf j'=\begin{bmatrix} b \\ d \end{bmatrix}
i′=[ac],j′=[bd]
实际上在各自的坐标系统,基向量均为 ( 1 , 0 ) , ( 0 , 1 ) (1,0),(0,1) (1,0),(0,1) 。特别的,两个坐标系原点的定义是一致的。
同一个向量在不同基向量下表示不同。在 Jennifer 的坐标系中,向量 v = [ x ′ y ′ ] \mathbf v=\begin{bmatrix} x' \\ y' \end{bmatrix} v=[x′y′],可以写成基向量的线性组合形式
v
=
x
′
i
′
+
y
′
j
′
\mathbf v=x'\mathbf i'+y'\mathbf j'
v=x′i′+y′j′
在 Grant 坐标系下的表示
v
=
x
′
[
a
c
]
+
y
′
[
b
d
]
\mathbf v=x'\begin{bmatrix} a \\ c \end{bmatrix}+y'\begin{bmatrix} b \\ d \end{bmatrix}
v=x′[ac]+y′[bd]
进一步,因为是线性变换,所以将其转化为矩阵乘法
v
=
[
a
b
c
d
]
[
x
′
y
′
]
=
[
x
y
]
\mathbf v=\begin{bmatrix} a&b \\ c&d \end{bmatrix}\begin{bmatrix} x' \\ y' \end{bmatrix}=\begin{bmatrix} x \\ y \end{bmatrix}
v=[acbd][x′y′]=[xy]
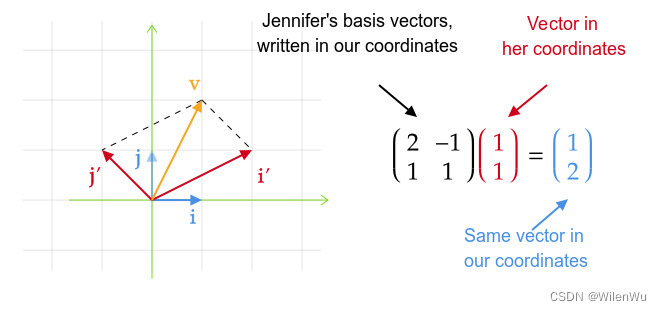
[ x y ] \begin{bmatrix} x \\ y \end{bmatrix} [xy] 和 [ x ′ y ’ ] \begin{bmatrix} x' \\ y’ \end{bmatrix} [x′y’] 实际是同一个向量,只不过是在不同基下的坐标。特别的,这里的 [ a b c d ] \begin{bmatrix} a&b \\ c&d \end{bmatrix} [acbd] 称为基变换矩阵,意味着同一个向量从 Jennifer 的坐标到 Grant 的坐标的映射,即以我们的视角描述 Jennifer 的向量。
进一步,我们将用基向量
i
′
,
j
′
\mathbf i',\mathbf j'
i′,j′ 描述的空间称为 “Jennifer’s grid”,用基向量
i
,
j
\mathbf i,\mathbf j
i,j 描述的空间称为 “Grant‘s grid”。在几何上,基变换矩阵表示的是将 Jennifer’s grid 在数值上用 Grant 的语言来描述。而逆变换则是将 Grant 的语言变成 Jennifer 的语言。
[
x
′
y
′
]
=
[
a
b
c
d
]
−
1
[
x
y
]
\begin{bmatrix} x' \\ y' \end{bmatrix}=\begin{bmatrix} a&b \\ c&d \end{bmatrix}^{-1}\begin{bmatrix} x \\ y \end{bmatrix}
[x′y′]=[acbd]−1[xy]
现讨论
n
n
n维线性空间
V
n
V_n
Vn 中的情形。任取
n
n
n 个线性无关的向量都可以作为
V
n
V_n
Vn 的一组基,对于不同的基,同一个向量的坐标是不同的。接下来,寻找同一个向量在不同基下的坐标之间的关系。
基变换公式:设矩阵
A
=
(
a
1
,
a
2
,
⋯
,
a
n
)
A=(\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n)
A=(a1,a2,⋯,an) 的列向量与
B
=
(
b
1
,
b
2
,
⋯
,
b
n
)
B=(\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n)
B=(b1,b2,⋯,bn) 的列向量是
n
n
n维线性空间
V
n
V_n
Vn 的两组基,则它们可以互相线性表示。若
{
b
1
=
p
11
a
1
+
p
21
a
2
+
⋯
+
p
n
1
a
n
b
2
=
p
12
a
1
+
p
22
a
2
+
⋯
+
p
n
2
a
n
⋯
b
n
=
p
1
n
a
1
+
p
2
n
a
2
+
⋯
+
p
n
n
a
n
\begin{cases} \mathbf b_1=p_{11}\mathbf a_1+p_{21}\mathbf a_2+\cdots+p_{n1}\mathbf a_n \\ \mathbf b_2=p_{12}\mathbf a_1+p_{22}\mathbf a_2+\cdots+p_{n2}\mathbf a_n \\ \cdots \\ \mathbf b_n=p_{1n}\mathbf a_1+p_{2n}\mathbf a_2+\cdots+p_{nn}\mathbf a_n \\ \end{cases}
⎩
⎨
⎧b1=p11a1+p21a2+⋯+pn1anb2=p12a1+p22a2+⋯+pn2an⋯bn=p1na1+p2na2+⋯+pnnan
利用分块矩阵的乘法形式,可将上式记为
B
=
A
P
B=AP
B=AP
称为基变换公式。其中,矩阵
P
=
[
p
11
p
12
⋯
p
1
n
p
21
p
22
⋯
p
2
n
⋮
⋮
⋱
⋮
p
n
1
p
2
n
⋯
p
n
n
]
P=\begin{bmatrix} p_{11}&p_{12}&\cdots&p_{1n} \\ p_{21}&p_{22}&\cdots&p_{2n} \\ \vdots&\vdots&\ddots&\vdots \\ p_{n1}&p_{2n}&\cdots&p_{nn} \\ \end{bmatrix}
P=
p11p21⋮pn1p12p22⋮p2n⋯⋯⋱⋯p1np2n⋮pnn
称为由基
A
=
{
a
1
,
a
2
,
⋯
,
a
n
}
A=\{\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n\}
A={a1,a2,⋯,an} 到
B
=
{
b
1
,
b
2
,
⋯
,
b
n
}
B=\{\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n\}
B={b1,b2,⋯,bn} 的过渡矩阵(transition matrix)。显然
P
−
1
P^{-1}
P−1 为由基
B
=
{
b
1
,
b
2
,
⋯
,
b
n
}
B=\{\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n\}
B={b1,b2,⋯,bn}到基
A
=
{
a
1
,
a
2
,
⋯
,
a
n
}
A=\{\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n\}
A={a1,a2,⋯,an}的过渡矩阵。
坐标变换公式:设线性空间
V
V
V 中的元素
v
\mathbf v
v 在基
A
=
{
a
1
,
a
2
,
⋯
,
a
n
}
A=\{\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n\}
A={a1,a2,⋯,an} 下的坐标为
v
A
\mathbf v_A
vA ,在基
B
=
{
b
1
,
b
2
,
⋯
,
b
n
}
B=\{\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n\}
B={b1,b2,⋯,bn} 下的坐标为
v
B
\mathbf v_B
vB ,则有
v
A
=
P
v
B
\mathbf v_A=P\mathbf v_B
vA=PvB
其中矩阵
P
P
P 为由基
A
=
{
a
1
,
a
2
,
⋯
,
a
n
}
A=\{\mathbf a_1,\mathbf a_2,\cdots,\mathbf a_n\}
A={a1,a2,⋯,an} 到
B
=
{
b
1
,
b
2
,
⋯
,
b
n
}
B=\{\mathbf b_1,\mathbf b_2,\cdots,\mathbf b_n\}
B={b1,b2,⋯,bn} 的过渡矩阵。
计算过渡矩阵:对于基变换公式
B
=
A
P
B=AP
B=AP ,可知过渡矩阵
P
=
A
−
1
B
P=A^{-1}B
P=A−1B 。写出增广矩阵
(
A
∣
B
)
,
(A\mid B) ,
(A∣B),用初等行变换把左边矩阵
A
A
A 处化为单位矩阵
I
I
I ,则右边出来的就是过渡矩阵
P
P
P,示意如下:
(
A
∣
B
)
→
(
I
∣
A
−
1
B
)
(A\mid B)\xrightarrow{}(I\mid A^{-1}B)
(A∣B)
(I∣A−1B)
例:设 b 1 = [ − 9 1 ] , b 2 = [ − 5 − 1 ] , c 1 = [ 1 − 4 ] , c 2 = [ 3 − 5 ] \mathbf b_1=\begin{bmatrix} -9 \\ 1 \end{bmatrix},\mathbf b_2=\begin{bmatrix} -5 \\ -1 \end{bmatrix},\mathbf c_1=\begin{bmatrix} 1 \\ -4 \end{bmatrix},\mathbf c_2=\begin{bmatrix} 3 \\ -5 \end{bmatrix} b1=[−91],b2=[−5−1],c1=[1−4],c2=[3−5] 考虑 R 2 \R^2 R2 中的基 B = { b 1 , b 2 } , C = { c 1 , c 2 } B=\{\mathbf b_1,\mathbf b_2\},C=\{\mathbf c_1,\mathbf c_2\} B={b1,b2},C={c1,c2} ,求 B B B 到 C C C 的过渡矩阵。
解:设基向量
c
1
,
c
2
\mathbf c_1,\mathbf c_2
c1,c2 在基
B
B
B 下的坐标分别为
[
c
1
]
B
=
[
x
1
x
2
]
,
[
c
2
]
B
=
[
y
1
y
2
]
[\mathbf c_1]_B=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix},\quad [\mathbf c_2]_B=\begin{bmatrix} y_1 \\ y_2 \end{bmatrix}
[c1]B=[x1x2],[c2]B=[y1y2]
由坐标的定义,可知
(
b
1
,
b
2
)
[
x
1
x
2
]
=
c
1
,
(
b
1
,
b
2
)
[
y
1
y
2
]
=
c
2
(\mathbf b_1,\mathbf b_2)\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}=\mathbf c_1,\quad (\mathbf b_1,\mathbf b_2)\begin{bmatrix} y_1 \\ y_2 \end{bmatrix}=\mathbf c_2
(b1,b2)[x1x2]=c1,(b1,b2)[y1y2]=c2
为了同步解出这两个方程组,使用增广矩阵
(
B
∣
C
)
(B\mid C)
(B∣C) 求解
(
b
1
,
b
2
∣
c
1
,
c
2
)
=
[
−
9
−
5
1
3
1
−
1
−
4
−
5
]
→
[
1
0
−
3
/
2
−
2
0
1
5
/
2
3
]
(\mathbf b_1,\mathbf b_2\mid \mathbf c_1,\mathbf c_2)= \begin{bmatrix}\begin{array}{cc:cc} -9&-5&1&3 \\ 1&-1&-4&-5 \end{array}\end{bmatrix}\to \begin{bmatrix}\begin{array}{cc:cc} 1&0&-3/2&-2 \\0&1&5/2&3 \end{array}\end{bmatrix}
(b1,b2∣c1,c2)=[−91−5−11−43−5]→[1001−3/25/2−23]
因此, 由
B
B
B 到
C
C
C 的过渡矩阵
P
=
[
−
3
/
2
−
2
5
/
2
3
]
P=\begin{bmatrix} -3/2&-2 \\5/2&3 \end{bmatrix}
P=[−3/25/2−23]
