转载请标明出处
目录
转载请标明出处
1.前言
2.数论函数介绍
2.1加性函数
2.1.1加性函数的性质
2.1.2一些加性函数的例子
2.2积性函数
2.2.1积性函数的性质
2.1.2一些积性函数的例子
2.3数论函数的重要操作
2.4一些非算术函数的例子
3.莫比乌斯函数
3.1定义
3.2性质
4.梅滕斯函数
4.1定义
4.2性质
5.刘维尔函数
5.1定义
5.2性质
6.卷积
6.1广义卷积
6.2狄利克雷卷积
6.2.1 定义
6.2.2 意义
6.2.3 具体计算
6.2.4 有关狄利克雷卷积意义下的交换群
7.莫比乌斯反演公式
7.1定义
7.1.1 因数反演公式
7.1.2 倍数反演公式(比较常用)
7.2 应用
7.2.1 计算 与 卷积的某一项
7.2.2 整数分块
7.2.3 计算 ,
8.参考文献
8.1 文章或其他资料的地址
8.2感谢
9.打“[x]”的式子的证明过程
9.1 为什么要给出证明
9.2具体证明
9.2.1 对式子[1]的证明
9.2.2 对式子[2]的证明
9.2.3 对式子[3]的证明
9.2.4 对式子[4]的证明
9.2.5 对式子[5]的证明
9.2.6 对式子[6]的证明
10.对“反演”的补充
10.1 概念
10.1. 1文字概念
10.1.2 数学概念
10.2几个常见的反演公式
10.2.1莫比乌斯反演
10.2.2二项式反演
10.2.3斯特林反演
10.2.4伯努利反演
10.2.5拉氏反演
11. 结语
1.前言
这篇博客在诞生之前,我对数论函数研究了两天,把一些最基本的概念和关系在这里做出相对详细的阐述,便于自己和网友的理解。
2.数论函数介绍
数论函数是算术函数的另一种叫法。数论函数分为了两种:加性函数和积性函数。
2.1加性函数
2.1.1加性函数的性质
加性函数具有以下性质:设函数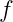 为加性函数,且
为加性函数,且 ,
,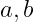 互质,则
互质,则 。
。
如果,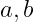 为任意数,也有
为任意数,也有 ,那么
,那么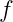 为完全加性函数
为完全加性函数
2.1.2一些加性函数的例子
有很多常见的加性函数,比如:

 ,表示
,表示 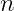 的质因子的数目(可算重复因子),其中,
的质因子的数目(可算重复因子),其中, 

 , 表示
, 表示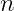 的相异因子数目
的相异因子数目

 , 表示所有
, 表示所有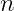 的质因子之和(可算重因子)
的质因子之和(可算重因子)

 , 表示所有
, 表示所有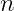 的相异因子之和
的相异因子之和
2.2积性函数
2.2.1积性函数的性质
 性质一
性质一
积性函数具有以下性质,设函数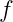 为积性函数,且
为积性函数,且 ,
, 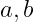 互质, 则
互质, 则 。
。
如果,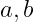 为任意数, 也有
为任意数, 也有 ,那么
,那么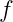 为完全积性函数
为完全积性函数
 性质二
性质二
设函数 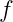 为积性函数,且有
为积性函数,且有  ,那么有
,那么有  . 若函数
. 若函数 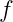 为完全积性函数,则
为完全积性函数,则

 性质三
性质三
设函数  ,
, 为积性函数,那么
为积性函数,那么  也为积性函数。
也为积性函数。
2.1.2一些积性函数的例子
有很多常见的积性函数,比如:

 , 欧拉函数, 表示与
, 欧拉函数, 表示与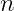 互质的数的数目
互质的数的数目

 , 莫比乌斯函数
, 莫比乌斯函数

 ,
, 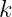 固定
固定

 , 刘维尔函数(完全积性函数),其中
, 刘维尔函数(完全积性函数),其中  ,
,  (加性函数,上面有提过)
(加性函数,上面有提过)

 , 单位函数(完全积性函数),其中
, 单位函数(完全积性函数),其中 
 所有狄利克雷特征的
所有狄利克雷特征的
2.3数论函数的重要操作
数论函数的重要操作是狄利克雷卷积(是卷积的一个子集)
2.4一些非算术函数的例子

 , 其中p是质数
, 其中p是质数

 , 表示不大于正整数
, 表示不大于正整数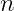 的素数数目
的素数数目

 , 表示整数
, 表示整数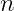 的拆分方案数目
的拆分方案数目
3.莫比乌斯函数
3.1定义
莫比乌斯函数记为 

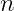 由
由 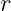 个不重因子组成时,是
个不重因子组成时,是 
3.2性质
 积性函数
积性函数
 无穷级数
无穷级数
 级数一:
级数一: 
 级数二:
级数二: 
 级数三:
级数三: 
 与刘维尔函数
与刘维尔函数 
 假设
假设  ,
,

 与欧拉函数
与欧拉函数 
4.梅滕斯函数
4.1定义
梅滕斯函数记为 

4.2性质
 非积性函数
非积性函数
 梅滕斯函数是莫比乌斯函数的求和
梅滕斯函数是莫比乌斯函数的求和
5.刘维尔函数
5.1定义
刘维尔函数记为  , 这在上面的积性函数中提到过
, 这在上面的积性函数中提到过
5.2性质
 完全积性函数
完全积性函数
 求和
求和 
 与莫比乌斯
与莫比乌斯 
6.卷积
6.1广义卷积
 连续卷积
连续卷积
设  在
在  上可积,
上可积,
则 
 离散卷积
离散卷积
设  在
在  上可积,
上可积,
则 ![(f * g )(n)=\sum_{m=-\infty }^{\infty}f[m]\cdot g[n-m]\Rightarrow \sum_{m=-\infty }^{\infty}f[n-m]\cdot g[m]](https://private.codecogs.com/gif.latex?%5Cdpi%7B150%7D%20%28f%20*%20g%20%29%28n%29%3D%5Csum_%7Bm%3D-%5Cinfty%20%7D%5E%7B%5Cinfty%7Df%5Bm%5D%5Ccdot%20g%5Bn-m%5D%5CRightarrow%20%5Csum_%7Bm%3D-%5Cinfty%20%7D%5E%7B%5Cinfty%7Df%5Bn-m%5D%5Ccdot%20g%5Bm%5D)
 计算方法
计算方法
 直接按定义计算
直接按定义计算
 快速傅里叶变换
快速傅里叶变换 
 分段卷积
分段卷积 
 数论变换
数论变换  快速数论变换
快速数论变换 
6.2狄利克雷卷积
6.2.1 定义
设  是两个数论函数,
是两个数论函数,
则 
6.2.2 意义
取两个算术函数,计算它们的狄利克雷卷积,则  就是积性函数
就是积性函数
6.2.3 具体计算
 计算一次的情况
计算一次的情况
设函数  已知且为积性函数,设
已知且为积性函数,设  ,求
,求 
for(int i=1;i*i<=n;++i)
{
if(n%i) continue;
h[n]+=f[i]*g[n/i];
if(i*i!=n)
h[n]+=f[n/i]*g[i];
}
 计算
计算 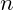 次的情况
次的情况
设函数  已知且为积性函数,设
已知且为积性函数,设  ,求
,求 
memset(h,0,sizeof(h));
for(int i=1;i<=n;++i)
for(int j=1;j*i<=n;++j)
h[i*j]+=f[i]*g[j];
6.2.4 有关狄利克雷卷积意义下的交换群
 单位元
单位元
狄利克雷交换群下的单位元,我们设为 
那么  必须满足 :设函数
必须满足 :设函数  为积性函数,则有
为积性函数,则有 

 积性函数在狄利克雷卷积意义下的逆
积性函数在狄利克雷卷积意义下的逆
设函数  为积性函数,若存在
为积性函数,若存在  , 则称
, 则称  为
为  的逆
的逆
 莫比乌斯函数与
莫比乌斯函数与 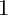 的卷积
的卷积
莫比乌斯函数与 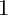 的关系:
的关系:  [1]
[1]
这意味着, 和
和 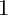 在狄利克雷卷积下互为逆元
在狄利克雷卷积下互为逆元
 欧拉函数与
欧拉函数与 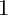 的卷积
的卷积
欧拉函数与 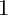 的关系:
的关系:  [2]
[2]
其中, 叫做单位函数(在积性函数提到过)
叫做单位函数(在积性函数提到过)
7.莫比乌斯反演公式
7.1定义
7.1.1 因数反演公式
设函数  为积性函数,设
为积性函数,设  , 那么有
, 那么有  [3]
[3]
7.1.2 倍数反演公式(比较常用)
设函数  为积性函数,设
为积性函数,设  , 那么有
, 那么有  [4]
[4]
所谓反演,即从和函数推导算术函数
7.2 应用
7.2.1 计算  与
与 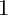 卷积的某一项
卷积的某一项
设函数  为积性函数,设函数
为积性函数,设函数  ,求
,求 
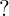

有  , 使用 Pollard_rho 算法分解因式,复杂度
, 使用 Pollard_rho 算法分解因式,复杂度 
而且  ,
,
通过化简, 我们就得到了  [5]
[5]
于是,计算  的时间复杂度变成了
的时间复杂度变成了 
7.2.2 整数分块
设函数  为积性函数,求
为积性函数,求 
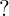
设  的值固定,那么
的值固定,那么  的浮动范围是
的浮动范围是 ![[\left \lfloor \frac{n}{\left \lfloor \frac{n}{i}\right \rfloor+1} +1\right \rfloor,\left \lfloor \frac{n}{\left \lfloor \frac{n}{i} \right \rfloor} \right \rfloor]](https://private.codecogs.com/gif.latex?%5Cinline%20%5Cdpi%7B150%7D%20%5B%5Cleft%20%5Clfloor%20%5Cfrac%7Bn%7D%7B%5Cleft%20%5Clfloor%20%5Cfrac%7Bn%7D%7Bi%7D%5Cright%20%5Crfloor+1%7D%20+1%5Cright%20%5Crfloor%2C%5Cleft%20%5Clfloor%20%5Cfrac%7Bn%7D%7B%5Cleft%20%5Clfloor%20%5Cfrac%7Bn%7D%7Bi%7D%20%5Cright%20%5Crfloor%7D%20%5Cright%20%5Crfloor%5D) .
.
我们可以预先处理  函数的前缀和,这样可以
函数的前缀和,这样可以  算
算  的区间和,时间复杂度变成了
的区间和,时间复杂度变成了 
7.2.3 计算  ,
,
化简得到:  [6]
[6]
8.参考文献
8.1 文章或其他资料的地址
1https://www.zhihu.com/question/23764267/answer/26007647
2.https://wenku.baidu.com/view/fbec9c63ba1aa8114431d9ac.html
3.https://www.cnblogs.com/zhouzhendong/p/8627380.html
4.https://blog.csdn.net/skywalkert/article/details/50500009
5.https://blog.csdn.net/jk_chen_acmer/article/details/82712276
6.https://blog.csdn.net/qq_41157137/article/details/83474978
7.https://wenku.baidu.com/view/f87f4b55b14e852459fb572b.html?from=search
8.https://baike.baidu.com/item/%E5%BA%8F%E5%88%97%E5%8F%8D%E6%BC%94/18894077?fr=aladdin
9.https://blog.csdn.net/hhaannyyii/article/details/79335883
8.2感谢
在此,向以上原创作者表示衷心的感谢
9.打“[x]”的式子的证明过程
9.1 为什么要给出证明
在上面的文章中,有一些式子的结尾带有“[x]”的标记,x是数字。表明这个式子最好需要能够给出证明过程,因为可以加深印象
9.2具体证明
9.2.1 对式子[1]的证明

![\therefore \mu *1 = [e==1]](https://private.codecogs.com/gif.latex?%5Cinline%20%5Cdpi%7B150%7D%20%5Ctherefore%20%5Cmu%20*1%20%3D%20%5Be%3D%3D1%5D)
9.2.2 对式子[2]的证明

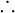 即证明
即证明 
 即证明
即证明 
设  ,
,
引理1: (
( 是质数)
是质数)
证明引理1:显然,在  ~
~  中,只有
中,只有  的倍数与
的倍数与  不互质,那么共有
不互质,那么共有  个数与
个数与  不互质,那么就有
不互质,那么就有  个数与
个数与  互质。
互质。
引理2:  (
( 是质数)
是质数)
证明引理2:由引理1显然

那么原式就等于 
显然,由引理2,我们可以得到: 
9.2.3 对式子[3]的证明
证明这个式子,我所知道的有两种方法:
 方法一(单位元法)
方法一(单位元法)





 方法二
方法二


最后一个等号的成立,是因为只有当  时,
时, 
9.2.4 对式子[4]的证明




最后一个等号的成立的原因同上
9.2.5 对式子[5]的证明





9.2.6 对式子[6]的证明

![=\sum_{d=1}^{n}f(d)\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)==d]](https://private.codecogs.com/gif.latex?%5Cinline%20%5Cdpi%7B150%7D%20%3D%5Csum_%7Bd%3D1%7D%5E%7Bn%7Df%28d%29%5Csum_%7Bi%3D1%7D%5E%7Bn%7D%5Csum_%7Bj%3D1%7D%5E%7Bm%7D%5Bgcd%28i%2Cj%29%3D%3Dd%5D)
![=\sum_{d=1}^{n}f(d)\sum_{d*i=1}^{n}\sum_{d*j=1}^{m}[gcd(d*i,d*j)==d]](https://private.codecogs.com/gif.latex?%5Cinline%20%5Cdpi%7B150%7D%20%3D%5Csum_%7Bd%3D1%7D%5E%7Bn%7Df%28d%29%5Csum_%7Bd*i%3D1%7D%5E%7Bn%7D%5Csum_%7Bd*j%3D1%7D%5E%7Bm%7D%5Bgcd%28d*i%2Cd*j%29%3D%3Dd%5D)
![=\sum_{d=1}^{n}f(d)\sum_{i=1}^{\left \lfloor \frac{n}{d} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{m}{d} \right \rfloor}[gcd(i,j)==1]](https://private.codecogs.com/gif.latex?%5Cinline%20%5Cdpi%7B150%7D%20%3D%5Csum_%7Bd%3D1%7D%5E%7Bn%7Df%28d%29%5Csum_%7Bi%3D1%7D%5E%7B%5Cleft%20%5Clfloor%20%5Cfrac%7Bn%7D%7Bd%7D%20%5Cright%20%5Crfloor%7D%5Csum_%7Bj%3D1%7D%5E%7B%5Cleft%20%5Clfloor%20%5Cfrac%7Bm%7D%7Bd%7D%20%5Cright%20%5Crfloor%7D%5Bgcd%28i%2Cj%29%3D%3D1%5D)
设 ![g(d,n,m)=\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)==d]](https://private.codecogs.com/gif.latex?%5Cdpi%7B120%7D%20g%28d%2Cn%2Cm%29%3D%5Csum_%7Bi%3D1%7D%5E%7Bn%7D%5Csum_%7Bj%3D1%7D%5E%7Bm%7D%5Bgcd%28i%2Cj%29%3D%3Dd%5D)
设  , 有
, 有 ![f(d,n,m) = \sum_{d|D}g(D,n,m)=\sum_{i=1}^{n}\sum_{j=1}^{m}[d|gcd(i,j)]=\left \lfloor \frac{n}{d} \right \rfloor \cdot \left \lfloor \frac{m}{d} \right \rfloor](https://private.codecogs.com/gif.latex?%5Cinline%20%5Cdpi%7B150%7D%20f%28d%2Cn%2Cm%29%20%3D%20%5Csum_%7Bd%7CD%7Dg%28D%2Cn%2Cm%29%3D%5Csum_%7Bi%3D1%7D%5E%7Bn%7D%5Csum_%7Bj%3D1%7D%5E%7Bm%7D%5Bd%7Cgcd%28i%2Cj%29%5D%3D%5Cleft%20%5Clfloor%20%5Cfrac%7Bn%7D%7Bd%7D%20%5Cright%20%5Crfloor%20%5Ccdot%20%5Cleft%20%5Clfloor%20%5Cfrac%7Bm%7D%7Bd%7D%20%5Cright%20%5Crfloor)
由倍数反演,得到:

 要求
要求 
 求
求 





10.对“反演”的补充
10.1 概念
10.1. 1文字概念
我们说“反演”,那么相对的就会有“正演”。
所谓”正演“就是知道了原因,就能推导出结果。
而所谓”反演“就是知道了结果,就能反推导出原因。
10.1.2 数学概念
注:这里的反演指的是“级数之间的互反关系”或者“整数序列的互反关系”
设两个函数  若有如下关系的一种:
若有如下关系的一种:


那么,另一种个关系必然成立,在下面介绍的几个反演公式中也用这两种方程表示
其中, 是 系数矩阵
是 系数矩阵
10.2几个常见的反演公式
10.2.1莫比乌斯反演
上面提到过,这里不再赘述
10.2.2二项式反演


10.2.3斯特林反演
这里,斯特林反演包含了“第一类斯特林数”和“第二类斯特林数”之间的关系


其中, 表示第一类斯特林数,
表示第一类斯特林数, 表示第二类斯特林数
表示第二类斯特林数
10.2.4伯努利反演
 伯努利数介绍
伯努利数介绍
伯努利数的前几项分别为:
特点:除  以外,所有奇数项的 伯努利数均为0
以外,所有奇数项的 伯努利数均为0
伯努利数的递推式:![B_n=[n==0] - \sum_{i=0}^{n-1} \frac{B_i}{n-i+1} \cdot \binom{n}{i}](https://private.codecogs.com/gif.latex?%5Cinline%20%5Cdpi%7B150%7D%20B_n%3D%5Bn%3D%3D0%5D%20-%20%5Csum_%7Bi%3D0%7D%5E%7Bn-1%7D%20%5Cfrac%7BB_i%7D%7Bn-i+1%7D%20%5Ccdot%20%5Cbinom%7Bn%7D%7Bi%7D)
其中 ![[n==0]=\begin{cases} 1 & \text{ if } x=0 \\ 0 & \text{ if } x>0 \end{cases}](https://private.codecogs.com/gif.latex?%5Cinline%20%5Cdpi%7B150%7D%20%5Bn%3D%3D0%5D%3D%5Cbegin%7Bcases%7D%201%20%26%20%5Ctext%7B%20if%20%7D%20x%3D0%20%5C%5C%200%20%26%20%5Ctext%7B%20if%20%7D%20x%3E0%20%5Cend%7Bcases%7D)
 伯努利数在求等幂级数上的应用
伯努利数在求等幂级数上的应用
所谓等幂级数,就是: 
利用伯努利数,化简得到:
现在,让我们思考一下,如果 如果用直接计算的方法,来算第一个等式的话,
如果用直接计算的方法,来算第一个等式的话,
时间复杂度变成了  , 明显超时
, 明显超时
但是,如果采用经过化简得第二个式子的话,时间复杂度变成了 
但是,实际上,第二个式子是得到了一个关于在 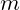 变化的基础上得到的一个关于
变化的基础上得到的一个关于 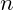 的通项公式
的通项公式
这里我写出伯努利数分子分母的  号码:分子:A027641, 分母:A027642
号码:分子:A027641, 分母:A027642
 伯努利反演
伯努利反演


10.2.5拉氏反演
 拉氏数(也叫
拉氏数(也叫  数)
数)
拉氏数的通项公式是:
拉氏数的递推式是:
其中,
还有,
 拉氏反演
拉氏反演


11. 结语
有任何问题,欢迎留言