本文仅用于个人学习记录,使用的教材为汤家凤老师的《高等数学辅导讲义》。本文无任何盈利或者赚取个人声望的目的,如有侵权,请联系删除!
一、函数基础知识
1.1 基本初等函数和初等函数
关于什么是函数,什么是反函数,这里就不再赘述,这里列举一下基本初等函数
| 函数名称 |
函数 |
| 幂函数 |
xa
|
| 指数函数 |
ax(a > 0且a ≠ 1) |
| 对数函数 |
logax(a > 0且a ≠ 1) |
| 三角函数 |
sinx,cosx,tanx,cotx,secx,cscx |
| 反三角函数 |
arcsinx,arccosx,arctantx,arccotx |
三角函数的基本关系
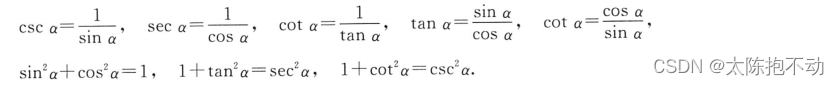
三角函数重要公式

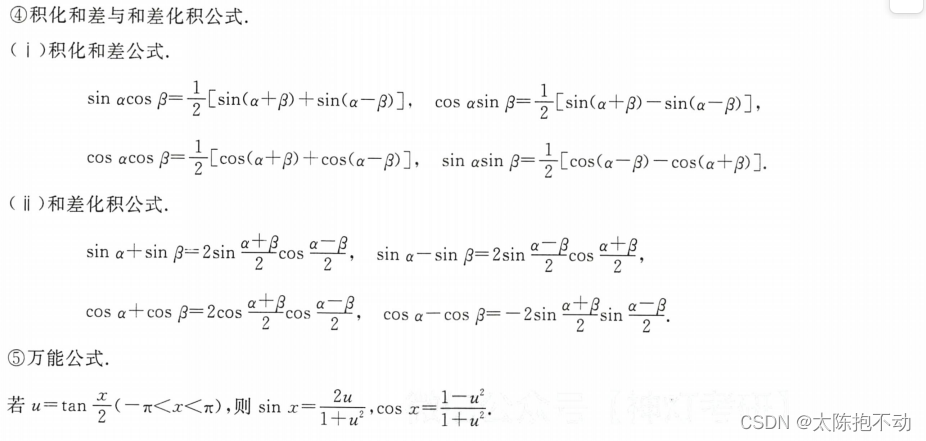
指数运算法则
对数运算法则

下面贴出基本初等函数的图形
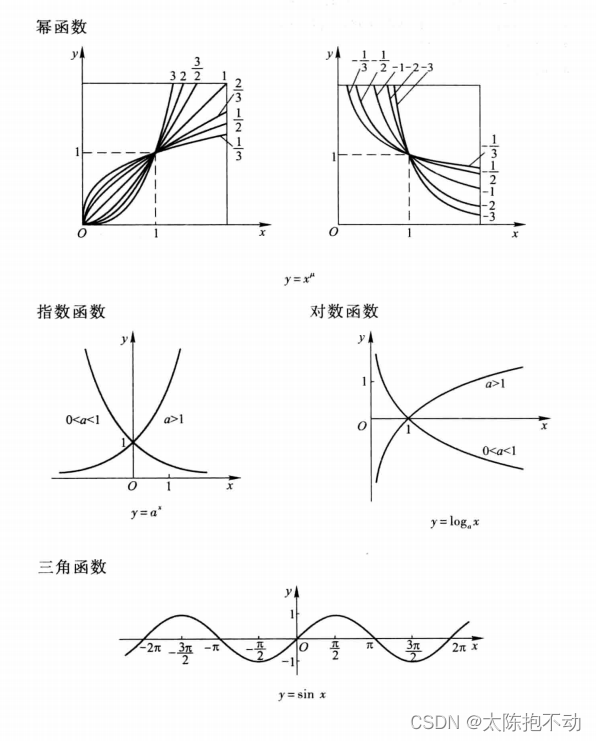

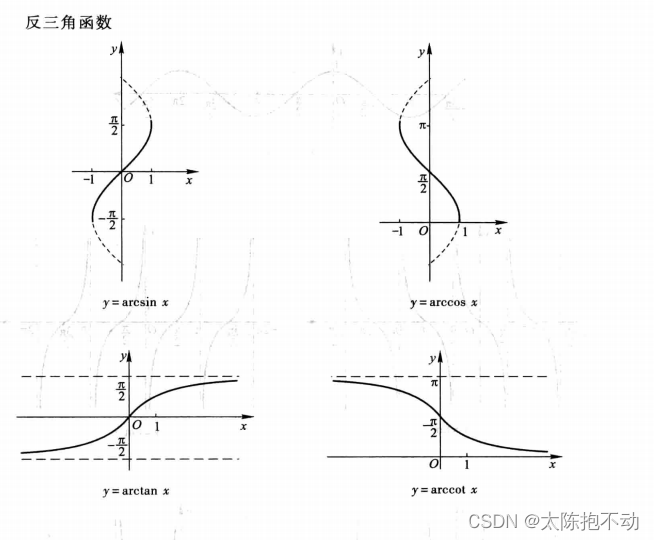
1.2 函数的初等特性
| 初等特性 |
说明 |
| 有界性 |
y = f(x),(x∈D)。若∃M > 0,对∀x∈D,总有|f(x)| ≤ M,称函数f(x)在D上有界 |
| 单调性 |
y = f(x),x∈D。若对∃x1,x2∈D,且x1 < x2,总有f(x1) < f(x2),称f(x)在D上单调递增。反之,单调递减 |
| 奇偶性 |
函数图形关于原点对称为奇函数,关于y轴对称为偶函数。用公式表达为f(-x) = -f(x)为奇函数;f(-x) = f(x)为偶函数。 |
| 周期性 |
y = f(x),(x∈D)。若∃T > 0,对∀x∈D,x ± T ∈D,有f(x ± T) = f(x),称f(x)是以T为周期的周期函数。 |
注:有界又可以分为有上界和有下界。函数f(x)有界的充要条件是,f(x)既有上界又有下界。
1.3 特殊函数
- 符号函数sgn x
- 狄利克雷函数D(x)。狄利克雷函数处处不连续,处处极限不存在,不可积分,是偶函数。
- 取整函数
关于取整函数有以下内容
- [x] ≤ x
- [x + y] = [x] + [y]不一定成立
- [x + m] = [x] + m一定成立,其中m为一个整数
二、函数题目类型
函数题目通常有求定义域,求反函数,证明有界性,单调性,奇偶性和周期性。
2.1 求定义域
求定义域比较简单,可能有的限制有
- 分母不为零
- 基本初等函数本身的限制
- 二次根号下数值大于等于零
2.2 求反函数

求反函数的思路就是将y = f(x)转换成x = f(y)。本题目的关键点在于知道下面的一个等式
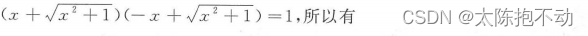
2.3 判断奇偶性

本题目需要明确几个知识点
- 定积分交换上下限时对积分变量取负即可,也就是∫axf(x)dx = ∫-a-xf(-x)d(-x)
- d(-x) = -d(x)
- 定积分的可加性,若a<c<b,则∫abf(x)dx = ∫acf(x)dx + ∫cbf(x)dx
三、极限基础知识
3.1 极限的定义
| 情形 |
定义 |
| 数列极限的定义(ε - N) |
对∀ε > 0,∃N > 0,当n > N时,有|an - A| ≤ ε,称A为数列an的极限,记为
lim
n
→
∞
\lim_{n\rightarrow\infty}
limn→∞an = A |
| 函数自变量趋于有限值的极限定义(ε - δ) |
对∀ε > 0,∃δ > 0,当0 < |x - a| < δ时,有|f(x) - A| < ε,称A为f(x)当x
→
\rightarrow
→a时的极限,记为
lim
x
→
\lim_{x\rightarrow}
limx→af(x) = A |
| 函数自变量趋于无穷大的极限定义(ε - X) |
对∀ε > 0,∃X > 0,当|x| > X时,有|f(x) - A| < ε,称A为f(x)当
x
→
∞
x\rightarrow\infty
x→∞时的极限,记为
lim
x
→
∞
\lim_{x\rightarrow\infty}
limx→∞f(x) = A |
| 自变量趋于
−
∞
-\infty
−∞时的极限定义 |
对∀ε > 0,∃X > 0,当x < -X时,有|f(x) - A| < ε,称A为f(x)当
x
→
−
∞
x\rightarrow-\infty
x→−∞时的极限,记为
lim
x
→
−
∞
\lim_{x\rightarrow-\infty}
limx→−∞f(x) = A |
| 自变量趋于
+
∞
+\infty
+∞时的极限定义 |
对∀ε > 0,∃X > 0,当x > X时,有|f(x) - A| < ε,称A为f(x)当
x
→
+
∞
x\rightarrow+\infty
x→+∞时的极限,记为
lim
x
→
+
∞
\lim_{x\rightarrow+\infty}
limx→+∞f(x) = A |
- 需要补充的是,我们要真正的理解定义,如果将自变量趋于有限值的极限定义中的|f(x) - A| < ε改为|f(x) - A| < 3ε,是否A还是函数f(x)趋于有限值的极限?答案是,定义依然成立。因为无论是ε还是3ε,都是任意的值,都是符合定义的。
- 除了上面说的,对于函数自变量趋于有限值的极限,还分为左极限和右极限。函数在一个点极限存在的充要条件是,函数在该点左极限和右极限存在且相等。
- 对于
lim
x
→
\lim_{x\rightarrow}
limx→a arctant
1
x
−
a
\frac{1}{x - a}
x−a1一定要分左右极限讨论。实际它的左右极限存在,但是不相等,一个为
Π
2
\frac{Π}{2}
2Π,一个为-
Π
2
\frac{Π}{2}
2Π。
- 若
lim
n
→
∞
\lim_{n\rightarrow\infty}
limn→∞an存在,则
lim
n
→
∞
\lim_{n\rightarrow\infty}
limn→∞|an|存在;反之,不对。
3.2 极限的性质
3.2.1 极限的一般性质
| 性质 |
叙述 |
| 唯一性 |
若极限存在,则极限一定是唯一的 |
| 保号性 |
lim
x
→
\lim_{x\rightarrow}
limx→af(x) = A > 0,则存在δ > 0,当0 < |x - a| < δ时,有f(x) > 0。函数极限正,则去心邻域正;函数极限负,则去心邻域负。 |
| 数列极限的有界性 |
极限存在,数列必有界;反之,不对。 |
| 函数极限的局部有界性 |
函数在某点的极限存在,则函数在其去心邻域内一定有界。 |
| 数列极限于子列极限的关系 |
(1) 若数列极限存在,则该数列的任意子列存在相同的极限;(2) 若任意子列极限存在,则该数列极限不一定存在。 |
对于极限的保号性有两条推论
- 函数不负,极限不负;函数不正,极限不负。也就是f(x) ≥ 0(或f(x) ≤ 0),且lim f(x) = A,则A ≥ 0(或A ≤ 0)。
- 函数的大小次序与极限的大小次序一致。即f(x) ≥ g(x),且lim f(x) = A,lim g(x) = B,则A ≥ B。
值得注意的是上面是≥和≤,如果改成>和<,则不一定正确。`
3.2.2 极限的运算性质
首先介绍一下极限的四则运算性质。设lim f(x) = A,lim g(x) = B。
- lim[f(x) ± g(x)] = lim f(x) + lim g(x) = A ±B
- lim f(x)g(x) = AB
- lim
f
(
x
)
g
(
x
)
\frac{f(x)}{g(x)}
g(x)f(x) =
A
B
\frac{A}{B}
BA,其中B ≠ 0
需要注意的是,如果lim f(x)或者lim g(x)不存在,则上面的性质不成立。
复合函数极限运算性质
- 设
lim
u
→
\lim_{u\rightarrow}
limu→af(u) = A,
lim
x
→
\lim_{x\rightarrow}
limx→x0 φ(x) = a,但是φ(x) ≠ a,则
lim
x
→
\lim_{x\rightarrow}
limx→x0 f[φ(x)] = A
- 设
lim
u
→
\lim_{u\rightarrow}
limu→af(u) = f(a),
lim
x
→
\lim_{x\rightarrow}
limx→x0 φ(x) = a,但是φ(x) ≠ a,则
lim
x
→
\lim_{x\rightarrow}
limx→x0 f[φ(x)] = f(a)
划重点
3.3 极限存在准则
3.3.1 夹逼定理
(数列型)设an ≤ bn ≤ cn,若
lim
n
→
∞
\lim_{n\rightarrow\infty}
limn→∞an = A,
lim
n
→
∞
\lim_{n\rightarrow\infty}
limn→∞cn = A,则
lim
n
→
∞
\lim_{n\rightarrow\infty}
limn→∞bn = A
(函数型)设f(x) ≤ g(x) ≤ h(x),lim f(x) = lim h(x) = A,则lim g(x) = A
需要注意的是,夹逼定理中的lim f(x) = lim h(x) = A,不可以用lim [f(x) - h(x)] = 0代替。
3.3.2 单调有界的数列必有极限
3.4 无穷小
3.4.1 无穷小的概念与比较
若
lim
x
→
\lim_{x\rightarrow}
limx→aα(x) = 0,称α(x)当x
→
\rightarrow
→a时为无穷小。
设α
→
\rightarrow
→ 0,β
→
\rightarrow
→ 0,若lim
β
α
\frac{β}{α}
αβ = 0,称β为α的高阶无穷小,记为β = o(α)。
若lim
α
β
\frac{α}{β}
βα = k(k ≠ 0),称β为α的同阶无穷小,记为β = O(α)。
若lim
α
β
\frac{α}{β}
βα = 1,称β为α的等价无穷小,记为α ~ β。
3.4.2 无穷小的性质
无穷小的基本性质
- 有限个无穷小的和、差、积仍为无穷小,常数与无穷小的积仍是无穷小。
- 有界函数与无穷小的积仍为无穷小。
- lim f(x) = A的充要条件是f(x) = A + α,其中α
→
\rightarrow
→ 0。
等价无穷小的性质
- α ~ β => β ~ α
- α ~ β,β ~ γ => α ~ γ
- 若α ~ α1,β ~ β1,且lim
β
1
α
1
\frac{β~1~}{α~1~}
α 1 β 1 = A,则lim
β
α
\frac{β}{α}
αβ = A
- α ~ β的充要条件是β = α + o(α)
x
→
0
\rightarrow\ 0
→ 0时,常用的一些等价无穷小
| 常用的等价无穷小 |
|---|
| x ~ sinx ~ tanx ~ arcsinx ~ arctantx ~ ln(1 + x) ~ ex - 1 |
| 1 - cosx ~
x
2
2
\frac{x^2}{2}
2x2
|
| 1 - cosax ~
a
2
\frac{a}{2}
2ax2
|
| (1 + x)a - 1 ~ ax (a ≠ 0) |
| ax - 1 ~ xlna |
3.5 两个重要的极限
lim
Δ
→
0
s
i
n
Δ
Δ
\lim_{Δ\rightarrow\ 0}\frac{sinΔ}{Δ}
limΔ→ 0ΔsinΔ = 1
lim
Δ
→
0
\lim_{Δ\rightarrow\ 0}
limΔ→ 0(1 + Δ)1/Δ = e
3.6 几个常用不等式
- 当0 < α <
Π
2
\frac{Π}{2}
2Π时,sinα < α < tanα
- 当x ≥ 0时,sinx ≤ x
- 当x > 0时,ln(1 + x) < x
- 当x ≠ 0时,ex > 1 + x
四、极限题目类型
4.1 证明数列极限为某一个值
紧扣定义即可

4.2 利用保号性判断极值点
利用保号性判断极值点有两种方法
- 证明在其去心邻域内的值都小于或者大于该点函数值。
- 证明该点导数为0,且在该点两侧导数值异号。

本题需要明确以下内容
- 函数连续,则极限值等于函数值。
- 分母极限为0,整体极限存在,那么分子极限也为0。

本题需要明确以下知识点
4.3 求极限
求极限有常规的化简直接求,也有用到泰勒公式展开,二项式定理,或者用到夹逼定理,无穷小等价和两个重要极限来求。

本题需要明确以下知识点
- 二项式定理
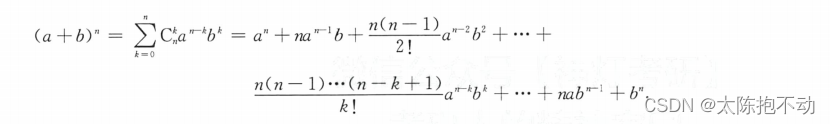
- Cnm =
n
!
m
!
(
n
−
m
)
!
\frac{n!}{m!(n-m)!}
m!(n−m)!n!

本题使用夹逼定理。

本题使用夹逼定理,关键点在于知道n! ≥ n(n - 1)(n - 2) (n ≥ 3)
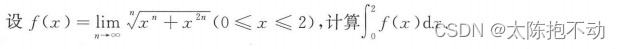
本题利用夹逼定理求出函数f(x)的表达式,然后计算积分。

本题使用两个常用的极限来求解。
五、连续与间断基础知识
5.1 函数连续性概念
- 函数f(x)在点x = a处连续 —— 设函数f(x)在x = a的邻域内有定义,若
lim
x
→
a
\lim_{x\rightarrow\ a}
limx→ af(x) = f(a)或f(a - 0) = f(a + 0) = f(a),称f(x)在x = a处连续。(极限值等于函数值)
- 若f(a - 0) = f(a),称f(x)在x = a处做连续;若f(a + 0) = f(a),称f(x)在x = a处右连续。
函数f(x)在[a,b]上连续 —— 设函数f(x)在[a,ba]上有定义,若满足
- f(x)在(a,b)内连续;
- f(a) = f(a + 0) = f(b - 0)
称函数f(x)在[a,b]上连续,记为f(x) ∈ [a,b]。
划重点
- 函数f(x)在点x = a处连续的充要条件是左极限等于右极限等于函数值。
- 若函数f(x)在点x = a处连续,则函数|f(x)|在点x = a处也连续。反之,不对。
- 若函数f(x)在点x = a处连续,则f(x)在点x = a的去心邻域内不一定连续。
5.2 间断点及分类
若
lim
x
→
a
\lim_{x\rightarrow\ a}
limx→ af(x) ≠ f(a),称f(x)在x = a处不连续,且x = a为f(x)的间断点。间断点的分类如下
| 间断点 |
描述 |
| 第一类间断点 |
若f(a - 0),f(a + 0)都存在,称x = a为f(x)的第一类间断点,即左右极限都存在,但是不等于函数值
|
| 可去间断点 |
若f(a - 0) = f(a + 0) ≠ f(a),称x = a为f(x)的可去间断点,即左右极限存在且相等,但是不等于函数值
|
| 跳跃间断点 |
若f(a - 0) ≠ f(a + 0),称x = a为f(x)的跳跃间断点,即左极限不等于右极限
|
| 第二类间断点 |
若f(a - 0),f(a + 0)至少有一个不存在,称x = a为f(x)的第二类间断点 |
5.3 闭区间上连续函数的性质
| 性质 |
描述 |
| 最值定理 |
若f(x) ∈ [a,b],则f(x)在[a,b]上一定存在最大值和最小值 |
| 有界定理 |
若f(x) ∈ [a,b],则f(x)在[a,b]上一定有界 |
| 零点定理 |
若f(x) ∈ [a,b],且f(a)f(b) < 0,则存在ξ ∈ (a,b),使得f(ξ) = 0 |
| 介值定理 |
若f(x) ∈ [a,b],对任意的η ∈ [m,M],则存在ξ ∈ [a,b],使得f(ξ) = η |
划重点
- 设f(x) ∈ [a,b],证明关于ξ ∈ (a,b)的命题时,一般使用零点定理。
- 设f(x) ∈ [a,b],证明关于ξ ∈ [a,b]的命题时,一般使用介值定理。
- 设f(x) ∈ [a,b],若出现函数值相加的条件,一般使用介值定理。
六、连续与间断题目类型
6.1 求间断点并分类
通常是看函数无定义的点,讨论左右极限,根据定义判断间断点类型。

6.2 利用闭区间上连续函数的性质证明命题

本题需要明确以下知识点
- 罗尔定理
设f(x)在[a,b]上连续,在(a,b)内可导,f(a) = f(b),则存在ξ ∈ (a,b),使得f(ξ) = 0。