TRMF 辅助论文：最小二乘法复现TRMF

2023-11-20

1 目标函数（总）

论文笔记:Temporal Regularized Matrix Factorization forHigh-dimensional Time Series Prediction_UQI-LIUWJ的博客-CSDN博客

$min_{W,X,\Theta} \frac{1}{2}\sum_{(i,t) \in \Omega} (y_it-w_ix_t^T)^2+\lambda_w R_w(W)+\lambda_x R_{AR}(X|\L,\Theta,\eta)+\lambda_\theta R_\theta(\Theta)$

1.1 求解W

我们留下含有W的部分：

$min_{W,X,\Theta} \frac{1}{2}\sum_{(i,t) \in \Omega} (y_it-w_ix_t^T)^2+\lambda_w R_w(W)$

$min_{W_i} \frac{1}{2} [(y_{i1}-w_ix_1^T)^2+\dots+(y_{in}-w_ix_n^T)^2]+ \frac{1}{2}\lambda_w\sum_{i=1}^m w_iw_i^T$

然后对wi求导

线性代数笔记：标量、向量、矩阵求导_UQI-LIUWJ的博客-CSDN博客

$\frac{1}{2} [-2(y_{i1}-w_ix_1^T)x_1+\dots+-2(y_{in}-w_ix_n^T)x_n]+ \frac{1}{2}\lambda_w 2I w_i=0$

$-(y_{i1}x_1+\dots+y_{in}x_n)+ [{(w_ix_1^T)x_1}+\dots+ (w_ix_n^T)x_n]+ \lambda_w I w_i=0$

而 $y_{ij}$ 是一个标量，所以放在xi的左边和右边没有影响

所以

$[{w_ix_1^Tx_1}+\dots+ w_ix_n^Tx_n]+ \lambda_w I w_i=(y_{i1}x_1+\dots+y_{in}x_n)$

也即：

$(\sum_{(i,t)\in \Omega}x_t^Tx_t) w_i+ \lambda_w I w_i=\sum_{(i,t)\in \Omega}y_{it}x_t$

$w_i=[(\sum_{(i,t)\in \Omega}x_t^Tx_t) + \lambda_w I]^{-1}\sum_{(i,t)\in \Omega}y_{it}x_t$

对应的代码如下：（假设sparse_mat表示观测矩阵）

from numpy.linalg import inv as inv
for i in range(dim1):
    #W矩阵的每一行分别计算
    pos0 = np.where(sparse_mat[i, :] != 0)
    #[num_obs] 表示i对应的有示数的数量

    Xt = X[pos0[0], :]
    #[num_obs,rank

    vec0 = sparse_mat[i, pos0[0]] @ Xt
    #sparse_mat[i, pos0[0]] 是一维向量，
    #所以sparse_mat[i, pos0[0]] @ Xt 和 sparse_mat[i, pos0[0]].T @ Xt 是一个意思，
    #输出的都是一个一维向量
    #[rank,1]

    mat0 = inv(Xt.T @ Xt + np.eye(rank))
    #[rank,rank]

    W[i, :] = mat0 @ vec0

其中：

$\sum_{(i,t)\in \Omega}y_{it}x_t$

vec0 = sparse_mat[i, pos0[0]] @ Xt

$[(\sum_{(i,t)\in \Omega}x_i^Tx_i) + \lambda_w I]^{-1}$

mat0 = inv(Xt.T @ Xt + np.eye(rank))

1.2 求解X

我们留下含有X的部分

$min_{W,X,\Theta} \frac{1}{2}\sum_{(i,t) \in \Omega} (y_it-w_ix_t^T)^2+\lambda_w R_w(W)+\lambda_x R_{AR}(X|\L,\Theta,\eta)$

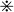$\lambda_x R_{AR}(X|\L,\Theta,\eta) =\frac{1}{2}\lambda_x \sum_{t=l_d+1}^f[(x_t-\sum_{l \in L}\theta_l \divideontimes x_{t-l})(x_t-\sum_{l \in L}\theta_l \divideontimes x_{t-l})^T]+\frac{1}{2}\lambda_x \eta \sum_{t=1}^f x_t x_t^T$

$\divideontimes$ 表示逐元素乘积 (两个向量a和b，a 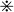$\divideontimes$ b可以用diag(a) b表示）

当t=1~ld的时候，我们没有 $R_{AR}$ 什么事情，所以此时我们更新X的方式和之前的W差不多 $min_{W,X,\Theta} \frac{1}{2}\sum_{(i,t) \in \Omega} (y_it-w_ix_t^T)^2+\lambda_x R_x(X)$

同理，X的更新方式为：

$\small x_t=[(\sum_{(i,t)\in \Omega}w_i^Tw_i) + \lambda_x \eta I]^{-1}\sum_{(i,t)\in \Omega}y_{it}w_i$

而当t≥ld+1的时候，我们就需要考虑 $R_{AR}$ 了

对于任意xt（我们令其为xo），他会出现在哪些 $R_{AR}$ 中呢？

首先是 $\frac{1}{2}\lambda_x[(x_o-\sum_{l \in L}\theta_l \divideontimes x_{o-l})(x_o-\sum_{l \in L}\theta_l \divideontimes x_{o-l})^T]$

$=\frac{1}{2}\lambda_x[(x_o-\sum_{l \in L}\theta_l \divideontimes x_{o-l})(x_o^T-(\sum_{l \in L}\theta_l \divideontimes x_{o-l})^T)]$

$\tiny =\frac{1}{2}\lambda_x[x_ox_o^T-(\sum_{l \in L}\theta_l \divideontimes x_{o-l})x_o^T-x_o(\sum_{l \in L}\theta_l \divideontimes x_{o-l})^T+(\sum_{l \in L}\theta_l \divideontimes x_{o-l})(\sum_{l \in L}\theta_l \divideontimes x_{o-l})^T]$

对xo求导，有：

$\small =\frac{1}{2}\lambda_x[2x_o-2\sum_{l \in L}\theta_l \divideontimes x_{o-l}]$

其次，是所有的 $\frac{1}{2}\lambda_x[(x_{o+l}-\sum_{l \in L}\theta_l \divideontimes x_{o})(x_{o+l}-\sum_{l \in L}\theta_l \divideontimes x_{o})^T]$

对每一个l，有用的项就是xo相关的项，于是我们可以写成，对每一个l的

$\frac{1}{2}\lambda_x[(x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l}-\theta_{l} \divideontimes x_{o})(x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l}-\theta_{l} \divideontimes x_{o})^T]$

$\small =\frac{1}{2}\lambda_x[(x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l})(x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l})^T -\theta_{l} \divideontimes x_{o}(x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l})^T -(x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l})(\theta_{l} \divideontimes x_{o})^T +\theta_{l} \divideontimes x_{o}(\theta_{l} \divideontimes x_{o})^T]$

对xo求导，有 $\small =\frac{1}{2}\lambda_x [-2\theta_{l} \divideontimes (x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l})^T+2(\theta_{l} ^2)\divideontimes x_o]$

还要注意一点，此时我们考虑的是下标为o+l的AR，所以o+l需要大于ld，小于T，也就是此时o的范围是o>ld-l ,<T-l【也就是说，在ld之前的xo也会有一定的AR的更新项】

于是我们可以写成

$\small \sum_{l \in L, o+l<T,o+l>l_d}\frac{1}{2}\lambda_x [-2\theta_{l} \divideontimes (x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l})^T+2(\theta_{l} ^2)\divideontimes x_o]$

几部分拼起来，有

$\small \sum_{l \in L, o+l<T, o>l_d}\frac{1}{2}\lambda_x [-2\theta_{l} \divideontimes (x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l})^T+2(\theta_{l} \divideontimes \theta_{l} ) \divideontimes x_o]$

$\small +\frac{1}{2}\lambda_x[2x_o-2\sum_{l \in L,o>l_d}\theta_l \divideontimes x_{o-l}]$

$\small +[(\sum_{(i,o)\in \Omega}w_i^Tw_i) + \lambda_x \eta I]x_o-\sum_{(i,o)\in \Omega}y_{io}w_i$

=0

$\small \sum_{l \in L, o+l<T, o>l_d}\lambda_x (\theta_{l} \divideontimes \theta_{l} ) \divideontimes x_o$

$\small +\lambda_x \eta I x_o$

$\small +[(\sum_{(i,o)\in \Omega}w_i^Tw_i) + \lambda_x I]x_o$

=

$\small \sum_{l \in L, o+l<T,o+l>l_d}\frac{1}{2}\lambda_x [-2\theta_{l} \divideontimes (x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l})^T+2(\theta_{l} ^2)\divideontimes x_o]$

+ $\small \sum_{(i,o)\in \Omega}y_{io}w_i$

所以xo（o≥ld+1）的更新公式为

$\small [(\sum_{(i,o)\in \Omega}w_i^Tw_i) + \lambda_x I+\lambda_x \eta I +\lambda_x\sum_{l \in L, o+l<T, o>l_d} diag(\theta_{l} \divideontimes \theta_{l} )]^{-1}$ [ $\small \sum_{l \in L, o+l<T,o+l>l_d}\frac{1}{2}\lambda_x [-2\theta_{l} \divideontimes (x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l})^T+2(\theta_{l} ^2)\divideontimes x_o]$ + $\small \sum_{(i,o)\in \Omega}y_{io}w_i$ ]

代码如下：

for t in range(2):
    pos0 = np.where(sparse_mat[:, t] != 0)
    #[num_obs] 表示i对应的有示数的数量
    Wt = W[pos0[0], :]
    #[num_obs,rank],t可见的wi
    Mt = np.zeros((rank, rank))
    #\sum diad (theta * theta)的那个矩阵
    Nt = np.zeros(rank)
    #Nt 相当于是 sum theta* x_{t-l}
    if t < np.max(time_lags):
        #这一个if，else考虑到的是首先的部分
        Pt = np.zeros((rank, rank))
        #t＜ld的时候，是没有λx I的
        Qt = np.zeros(rank)
        #t＜ld的时候，没有过去时间段的回归项
    else:
        Pt = np.eye(rank)
        #t>ld+1的时候 有λx I
        Qt = np.einsum('ij, ij -> j', theta, X[t - time_lags, :])
        #theta [d,rank]
        #X[t - time_lags, :] [d,rank]
        '''
        对于每一个theta和X[t - time_lags, :]中的j （j∈range(rank)）
        我们输出是一个rank长的向量，第j维是每个theta的(i,j)元素
            和对应的X的(i,j)元素相乘，然后求和
        每个theta的(i,j)元素表示向量第j个元素的第i个time lag的AR权重
        每个X的(i,j)元素表示向量第j个元素的第i个time lag的数据
        相乘再1求和，就是输出的第j个元素，有之前的时序数据加权求和得到的自归回值
        '''
        '''
        换一个角度理解，就是theta和X[t - time_lags, :]逐元素乘积，
        再从一个[d,rank]矩阵，压缩成一个rank长的向量
        即np.sum(theta*X[t - time_lags, :],axis=0)
        '''
    if t < dim2 - np.min(time_lags):
        #这个if 考虑的是其次的部分，所以需要t+l>ld 且t+l<T
        #（ld是max(time_lags),T是dim2
        #t+min(lag)小于T
        if t >= np.max(time_lags) and t < dim2 - np.max(time_lags):
            index = list(range(0, d))
         #t>=ld,同时t+max(ld)也没有超过最大的时间限制，此时所有的d个time lad都可以使用   
        else:
            index = list(np.where((t + time_lags >= np.max(time_lags)) 
                                  & (t + time_lags < dim2)))[0]
            #在两头，计算可以用的o+l
        for k in index:
            Ak = theta[k, :]
            #[rank]
            Mt += np.diag(Ak ** 2)
            #对应的是Σdiag(θk*θk)
            theta0 = theta.copy()
            theta0[k, :] = 0
            #第k行赋值为0的作用，就是Σ_{l'∈L-{l}}
            Nt += np.multiply(Ak, 
                              X[t + time_lags[k], :] - np.einsum(
                                          'ij, ij -> j',
                                          theta0,
                                          X[t + time_lags[k] - time_lags, :]))
            '''
            AK——θl [rank]
            X[t + time_lags[k], :] x_{o+l}
            
            np.einsum('ij, ij -> j',theta0, X[t + time_lags[k] - time_lags, :])
            对于每一个theta0和XX[t + time_lags[k] - time_lags, :]中的j （j∈range(rank)）
            我们输出是一个rank长的向量，第j维是每个theta的(i,j)元素
                    和对应的X的(i,j)元素相乘，然后求和
            每个theta的(i,j)元素表示向量第j个元素的第i个time lag的AR权重
            每个X的(i,j)元素表示向量第j个元素的第i个time lag的数据
            相乘再求和，就是输出的第j个元素，有之前的时序数据加权求和
                得到的自归回值(之前的时间序列不包括l，因为那一行被赋值为0了)
            '''
            #也就是Nt相当于其次括号里面的第一项
    vec0 = Wt.T @ sparse_mat[pos0[0], t] + lambda_x * Nt + lambda_x * Qt
    #Wt.T @ sparse_mat[pos0[0], t] [rank]
    #lambda_x * Nt  第一项
    #lambda_x * Qt 第二项
    mat0 = inv(Wt.T @ Wt + lambda_x * Mt + lambda_x * Pt + lambda_x * eta * np.eye(rank))
    #分别是第一项、第四项、第二项、第三项
    X[t, :] = mat0 @ vec0

vec0：

$\small \sum_{l \in L, o+l<T,o+l>l_d}\frac{1}{2}\lambda_x [-2\theta_{l} \divideontimes (x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l})^T+2(\theta_{l} ^2)\divideontimes x_o]$ + $\small \sum_{(i,o)\in \Omega}y_{io}w_i$ ]

mat0：

$\small [(\sum_{(i,o)\in \Omega}w_i^Tw_i) + \lambda_x I+\lambda_x \eta I +\lambda_x\sum_{l \in L, o+l<T, o>l_d} diag(\theta_{l} \divideontimes \theta_{l} )]^{-1}$

3 更新θ

$min_{W,X,\Theta} \frac{1}{2}\sum_{(i,t) \in \Omega} (y_it-w_ix_t^T)^2+\lambda_w R_w(W)+\lambda_x R_{AR}(X|\L,\Theta,\eta)+\lambda_\theta R_\theta(\Theta)$

我们留下和θ (θk)有关的部分

$\small \frac{1}{2}\lambda_x \sum_{t=l_d+1}^f[(x_t-\sum_{l \in L}\theta_l \divideontimes x_{t-l})(x_t-\sum_{l \in L}\theta_l \divideontimes x_{t-l})^T]+\lambda_\theta R_\theta(\Theta)$

$=\frac{1}{2}\lambda_x \sum_{t=l_d+1}^f[(x_t-\sum_{l \in L-\{k\}}\theta_l \divideontimes x_{t-l}-\theta_k \divideontimes x_{t-k})(x_t-\sum_{l \in L-\{k\}}\theta_l \divideontimes x_{t-l}-\theta_k \divideontimes x_{t-k})^T]+\lambda_\theta R_\theta(\Theta)$

$=\frac{1}{2}\lambda_x \sum_{t=l_d+1}^f[(x_t-\sum_{l \in L-\{k\}}\theta_l \divideontimes x_{t-l})(x_t-\sum_{l \in L-\{k\}}\theta_l \divideontimes x_{t-l})^T$

$-(x_t-\sum_{l \in L-\{k\}}\theta_l \divideontimes x_{t-l})(\theta_k \divideontimes x_{t-k})^T$

$-(\theta_k \divideontimes x_{t-k})(x_t-\sum_{l \in L-\{k\}}\theta_l \divideontimes x_{t-l})^T$

$+(\theta_k \divideontimes x_{t-k})(\theta_k \divideontimes x_{t-k})^T]$

$+\lambda_\theta R_\theta(\Theta)$

关于θk求导

$\small \frac{1}{2}\lambda_x \sum_{t=l_d+1}^f[-2(x_t-\sum_{l \in L-\{k\}}\theta_l \divideontimes x_{t-l})\divideontimes x_{t-k}+2 diag (x_{t-k} \divideontimes x_{t-k})\theta_k]+\lambda_\theta I \theta_k=0$

$\small \theta_k=[\lambda_\theta I + \sum_{t=l_d+1}^f diag (x_{t-k} \divideontimes x_{t-k})\theta_k]^{-1} \sum_{t=l_d+1}^f[(x_t-\sum_{l \in L-\{k\}}\theta_l \divideontimes x_{t-l})\divideontimes x_{t-k}]$

4 总结

$w_i=[(\sum_{(i,t)\in \Omega}x_t^Tx_t) + \lambda_w I]^{-1}\sum_{(i,t)\in \Omega}y_{it}x_t$

x:

t ∈ 1~ld： $\small x_t=[(\sum_{(i,t)\in \Omega}w_i^Tw_i) + \lambda_x \eta I]^{-1}\sum_{(i,t)\in \Omega}y_{it}w_i$

t ≥ld+1 $\small [(\sum_{(i,o)\in \Omega}w_i^Tw_i) + \lambda_x I+\lambda_x \eta I +\lambda_x\sum_{l \in L, o+l<T, o>l_d} diag(\theta_{l} \divideontimes \theta_{l} )]^{-1}$ [ $\small \sum_{l \in L, o+l<T,o+l>l_d}\frac{1}{2}\lambda_x [-2\theta_{l} \divideontimes (x_{o+l}-\sum_{l' \in L-\{l\}}\theta_{l'} \divideontimes x_{o+l'-l})^T+2(\theta_{l} ^2)\divideontimes x_o]$ + $\small \sum_{(i,o)\in \Omega}y_{io}w_i$ ]

$\small \theta_k=[\lambda_\theta I + \sum_{t=l_d+1}^f diag (x_{t-k} \divideontimes x_{t-k})\theta_k]^{-1} \sum_{t=l_d+1}^f[(x_t-\sum_{l \in L-\{k\}}\theta_l \divideontimes x_{t-l})\divideontimes x_{t-k}]$

本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容，请联系:hwhale#tublm.com(使用前将#替换为@)