【飞控算法】四旋翼飞行器控制原理与设计入门

2023-05-16

从动力学建模和几个四旋翼核心算法角度分析半自主飞控系统的建立，即实现传统四旋翼的姿态控制和高度控制的过程，文章主要借鉴了北航多旋翼设计课程、正点原子minifly微型四旋翼的资料、《四旋翼无人飞行器设计》清华出版社，代码示例来自正点原子。但是吧，后两个资料在理论部分都有点东拼西凑的感觉，有些错误，看起来很伤…总之，本文多处为个人理解，如有错误，感谢指出。

一、相关理论知识

1.坐标系与欧拉角

2.旋转矩阵

3.四元数及其与欧拉角的关系

二、控制模型建立

1.四旋翼动力学模型

2.简化为控制模型

3.四旋翼控制分配模型

三、控制算法及实现

1.姿态解算

2.串级PID控制

3.控制分配

一、相关理论知识

1.坐标系与欧拉角

进行动力学建模之前首先建立坐标系，在此建立地球坐标系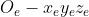 $O_{e}-x_{e}y_{e}z_{e}$ 和机体坐标系 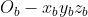$O_{b}-x_{b}y_{b}z_{b}$ ，如图所示，这里地球系z轴方向向下指向地心，机体系x轴为机头方向。

当描述一个三维空间内的刚体转动时，需要选用三个独立的角度来表示刚体的相对位置。即，刚体绕固定点的旋转可以看成是若干次旋转的合成，旋转方法不是唯一的，所以欧拉角有多种取法，不同的取法、不同的转动顺序都会对于不同的旋转矩阵。在研究四旋翼时，为了与四旋翼的滚转、俯仰、偏航相对应，可以取绕x旋转角度为φ（滚转，右滚为正），绕y轴旋转角度为θ（俯仰，仰头为正），绕z轴旋转为ψ（偏航，右偏为正）。

由地球坐标系转到机体坐标系为xyz旋转，又称卡尔丹角。实际上理论分析时，旋转顺序不是很重要，zyx、zxy都可以，虽然最后姿态解算时四元数与欧拉角的关系式不同，但是都可以进行解算。

2.旋转矩阵

绕x轴旋转的旋转矩阵为，

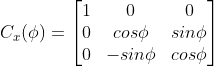
$C_{x}(\phi )=\begin{bmatrix} 1 & 0 & 0\\ 0 &cos\phi &sin\phi \\ 0& -sin\phi & cos\phi \end{bmatrix}$

绕y轴旋转的旋转矩阵为，

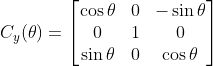
$C_{y}(\theta )=\begin{bmatrix} \cos \theta & 0&-\sin \theta \\ 0& 1 &0 \\ \sin \theta & 0 &\cos \theta \end{bmatrix}$

绕z轴旋转的旋转矩阵为，

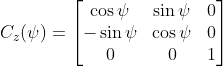
$C_{z}(\psi )=\begin{bmatrix} \cos \psi & \sin \psi &0 \\ -\sin \psi &\cos \psi&0 \\ 0& 0 &1 \end{bmatrix}$

这样，xyz旋转时，一个向量由地球系的表示转为机体系的表示，可以写成，

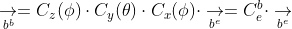
$\underset{b^{b}}{\rightarrow}=C_{z}( \phi )\cdot C_{y}(\theta )\cdot C_{x}(\phi )\cdot \underset{b^{e}}{\rightarrow}= C_{e}^{b}\cdot \underset{b^{e}}{\rightarrow}$

$C_{e}^{b}=\begin{bmatrix} \cos\theta \cos \psi &\sin \phi \sin \theta \cos \psi +\cos \phi \sin \psi & -\cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi \\ -\cos \theta \sin \psi & -\sin \phi \sin \theta \sin \psi +\cos \phi \cos \psi & \cos \phi \sin \theta \sin \psi +\sin \phi \cos \psi \\ \sin \theta &- \sin \phi \cos \theta & \cos \phi\cos \theta \end{bmatrix}$

由机体系转向地球系的姿态矩阵为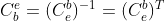， $C_{b}^{e}=(C_{e}^{b})^{-1}=(C_{e}^{b})^{T}$

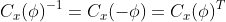
${C_{x}(\phi )}^{-1}=C_{x}(-\phi )={C_{x}(\phi )}^{T}$

3.四元数及其与欧拉角的关系

关于四元数的详细定义等参见秦永元的《惯性导航》，非常详细，这里不搬了。

以zyx旋转顺序为例，此时其旋转矩阵

$C_{e}^{b}=\begin{bmatrix} \cos\theta \cos \psi &\sin \psi \cos \theta &- \sin \theta \\\sin \phi \sin \theta \cos \psi -\cos \phi \sin \psi & \sin \phi \sin \theta \sin \psi +\cos \phi \cos \psi &\sin \phi \cos \theta\\ \cos \phi \sin \theta \cos \psi +\sin \phi \sin \psi & \cos \phi \sin \theta \sin \psi -\sin \phi \cos \psi & \cos \phi\cos \theta \end{bmatrix}$

此时由四元数表示的旋转为

$\begin{bmatrix} x_{b}\\ y_{b} \\ z_{b} \end{bmatrix}=\begin{bmatrix} q_{0}^{2}+ q_{1}^{2}- q_{2}^{2}- q_{3}^{2}&2(q_{1}q_{2}+q_{0}q_{3}) &2(q_{1}q_{3}-q_{0}q_{2}) \\ 2(q_{1}q_{2}-q_{0}q_{3}) &q_{0}^{2}- q_{1}^{2}+q_{2}^{2}- q_{3}^{2} &2(q_{2}q_{3}+q_{0}q_{1}) \\ 2(q_{1}q_{3}+q_{0}q_{2}) & 2(q_{2}q_{3}-q_{0}q_{1}) & q_{0}^{2}-q_{1}^{2}- q_{2}^{2}+q_{3}^{2} \end{bmatrix}\begin{bmatrix} x_{e}\\ y_{e} \\ z_{e} \end{bmatrix}$

这样一一对应，可以求得后面姿态解算时要用到的一些式子，

①重力在机体坐标系下的表示：

$\begin{bmatrix} Vx_{b}\\ Vy_{b} \\ Vz_{b} \end{bmatrix}\\=\begin{bmatrix} q_{0}^{2}+ q_{1}^{2}- q_{2}^{2}- q_{3}^{2}&2(q_{1}q_{2}+q_{0}q_{3}) &2(q_{1}q_{3}-q_{0}q_{2}) \\ 2(q_{1}q_{2}-q_{0}q_{3}) &q_{0}^{2}- q_{1}^{2}+q_{2}^{2}- q_{3}^{2} &2(q_{2}q_{3}+q_{0}q_{1}) \\ 2(q_{1}q_{3}+q_{0}q_{2}) & 2(q_{2}q_{3}-q_{0}q_{1}) & q_{0}^{2}-q_{1}^{2}- q_{2}^{2}+q_{3}^{2} \end{bmatrix}\begin{bmatrix} 0\\0\\1\end{bmatrix} \\=\begin{bmatrix} 2(q_{1}q_{3}-q_{0}q_{2})\\ 2(q_{2}q_{3}+q_{0}q_{1}) \\ q_{0}^{2}-q_{1}^{2}- q_{2}^{2}+q_{3}^{2} \end{bmatrix}$

②四元数与欧拉角的关系：

$\phi =\arctan \frac{2(q_{2}q_{3}+q_{0}q_{1})}{q_{0}^{2}-q_{1}^{2}- q_{2}^{2}+q_{3}^{2}}$

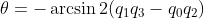
$\theta =-\arcsin 2(q_{1}q_{3}-q_{0}q_{2})$

$\psi =\arctan \frac{2(q_{1}q_{2}+q_{0}q_{3})}{q_{0}^{2}+q_{1}^{2}- q_{2}^{2}-q_{3}^{2} }$

四元数具体的推导和计算太多了，详见《捷联式惯性导航原理》。关于四元数与旋转矩阵我查阅了很多资料，比较官方的书呢，推导都是用的zyx旋转顺序，推出上式中四元数与欧拉角的关系。其他资料呢，有用不同的旋转顺序，但是对应旋转矩阵时很容易搞错。我觉得四元数与欧拉角的关系不是唯一的，只取决于使用的四元数，旋转顺序不同，对应的四元数自然不同。这主要影响的是解算过程中，q的值可能是不同的，但解算出的欧拉角都是一样的。

二、控制模型建立

首先，建模的目的是基于这个模型设计控制器。四旋翼是一个非线性的多输入系统，但是，为了简化处理，在小角度时，可以将模型简化为线性的，进而就可以使用线性控制的方法处理。

1.四旋翼动力学模型

①欧拉角表示为，

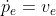
$\dot{p}_{e}=v_{e}$

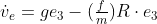
$\dot{v}_{e}=ge_{3}-(\tfrac{f}{m})R\cdot e_{3}$

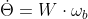
$\dot{\Theta }=W\cdot \omega _{b}$

$J\cdot\dot{\omega _{b}}=-\omega _{b}\times (J\times \omega _{b})+G_{a}+\tau$

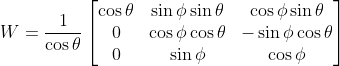
其中， $W=\frac{1}{\cos \theta }\begin{bmatrix} \cos \theta &\sin \phi \sin \theta &\cos \phi \sin \theta \\ 0&\cos \phi \cos \theta &-\sin \phi \cos \theta \\ 0 & \sin \phi &\cos \phi \end{bmatrix}$

②四元数表示为，

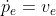
$\dot{p}_{e}=v_{e}$

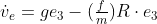
$\dot{v}_{e}=ge_{3}-(\tfrac{f}{m})R\cdot e_{3}$

$\dot{q_{0}}=-\frac{1}{2}{q_{v}}^{T}\cdot \omega _{b}$

$\dot{q_{v}}=\frac{1}{2}(q_{0}\cdot I_{3}+\begin{bmatrix} q_{v} \end{bmatrix}_{\times })\cdot \omega _{b}$

（上面两个式子实际上是四元数运动学微分方程，后面姿态解算时会用到）

$J\cdot\dot{\omega _{b}}=-\omega _{b}\times (J\times \omega _{b})+G_{a}+\tau$

2.简化为控制模型

在这里研究给定期望姿态角，期望高度的控制模型，这样可以分为四个通道：高度通道、俯仰通道、滚转通道、偏航通道，俯仰通道、滚转通道、偏航通道模型是一样的，是姿态模型。

①先看高度通道（z方向）的化简，

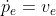
$\dot{p}_{e}=v_{e}$

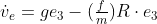
$\dot{v}_{e}=ge_{3}-(\tfrac{f}{m})R\cdot e_{3}$

变为，

$\dot{p}_{z}=v_{z}$

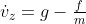$\dot{v}_{z}=g-\tfrac{f}{m}$ （俯仰、滚转都很小时）

②再看姿态通道的化简，

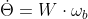
$\dot{\Theta }=W\cdot \omega _{b}$

$J\cdot\dot{\omega _{b}}=-\omega _{b}\times (J\times \omega _{b})+G_{a}+\tau$

变为，

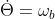
$\dot{\Theta }= \omega _{b}$

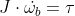$J\cdot\dot{\omega _{b}}=\tau$ （角度小，速度小时）

3.四旋翼控制分配模型

控制分配模型是建立伪控制量与实际控制量之间关系的模型，以X4型传统四旋翼为例，其伪控制量实际是几个通道经过pid之后的输出值pidout，高度通道的输出可以看做是总拉力，.姿态通道可以看成是力矩（具体分析就涉及到pid控制器的设计了）；其实际控制量可以看成是电机转速的平方。这几个伪控制量与实际控制量的对应关系如下：

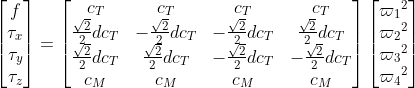$\begin{bmatrix} f\\ \tau _{x} \\ \tau _{y} \\ \tau _{z} \end{bmatrix}= \begin{bmatrix} c_{T} & c_{T} &c_{T} &c_{T} \\ \frac{\sqrt{2}}{2}dc_{T} &-\frac{\sqrt{2}}{2}dc_{T} &-\frac{\sqrt{2}}{2}dc_{T} & \frac{\sqrt{2}}{2}dc_{T} \\ \frac{\sqrt{2}}{2}dc_{T} &\frac{\sqrt{2}}{2}dc_{T} &-\frac{\sqrt{2}}{2}dc_{T} & -\frac{\sqrt{2}}{2}dc_{T} \\ c_{M} & c_{M} &c_{M} & c_{M} \end{bmatrix}\begin{bmatrix} {\varpi _{1}}^{2}\\ {\varpi _{2}}^{2} \\ {\varpi _{3}}^{2} \\ {\varpi _{4}}^{2} \end{bmatrix}$ ,其中 $c_{T}$ 是电机转速平方与拉力之间的关系系数， $c_{M}$ 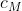是电机转速平方与反扭力之间的关系系数，d是机臂长度。

控制分配模型在普通四旋翼上的分配基本是固定的，但是当伪控制量与实际控制量个数不一致时，控制分配就很重要。

三、控制算法及实现

全自主飞控的控制逻辑是从给定期望轨迹和期望偏航开始的，首先经过这一位置控制得到期望的拉力和期望的三个姿态角，在这里，我暂不考虑轨迹控制，即飞控的逻辑是从给定期望姿态角和期望高度开始。

这样，飞控底层框架大致如下图，

图比较乱，硬件、算法、数据都在里面了，基本能看懂…可以看出，四旋翼的三个核心算法：姿态解算算法、pid控制算法、控制分配算法。

1.姿态解算

四旋翼姿态解算的方法有很多，有基于四元数，有基于旋转矩阵，有互补滤波，有卡尔曼滤波，其实不管是哪种滤波解算的算法，思想都是利用加速度计解算出得数据去修正陀螺仪积分产生偏差。在这里我主要研究了一下最常用的，四元数互补滤波，这个资料已经比较全了，每一个步骤我只记录一下我的理解。

（1）初始化四元数

static float q0 = 1.0f;	
static float q1 = 0.0f;
static float q2 = 0.0f;
static float q3 = 0.0f;

（2）加速度计低通滤波，去除一部分高频噪声，获取加速度计、陀螺仪值

（3）加速度计测量值规范化

normalise = invSqrt(acc.x * acc.x + acc.y * acc.y + acc.z * acc.z);
acc.x *= normalise;
acc.y *= normalise;
acc.z *= normalise;

（4）提取四元数的等效余弦矩阵中的重力分量

vecxZ = 2 * (q1 * q3 - q0 * q2);
vecyZ = 2 * (q0 * q1 + q2 * q3);
veczZ = q0s - q1s - q2s + q3s;

（5）向量叉积得出偏差

ex = (acc.y * veczZ - acc.z * vecyZ);
ey = (acc.z * vecxZ - acc.x * veczZ);
ez = (acc.x * vecyZ - acc.y * vecxZ);

（6）PI修正陀螺仪

exInt += Ki * ex * dt ;  
eyInt += Ki * ey * dt ;
ezInt += Ki * ez * dt ;
gyro.x += Kp * ex + exInt;
gyro.y += Kp * ey + eyInt;
gyro.z += Kp * ez + ezInt;

解释一下（5）、（6），首先在（3）、（4）中保证了加速度计表示的重力分量和由四元数推算出的重力分量都是单位的，这样（5）中的偏差实际上可以理解为角度，且都是在机体坐标系中，我们知道，陀螺仪虽然噪音小，但是其值会有漂移，如果通过积分计算角度，随着时间，其值会累积，这样就得不到准确值了，越偏越多，而加速度计没有漂移，但是噪音很大，且测量值稳定后，即为实际的真值。这样就考虑用加速度计去修正陀螺仪的偏差。实际上，个人理解，这里的姿态误差就可以看成是输入pi控制器的ref-fdb，而通过pi修正之后，得出的out，就可以用了消除陀螺仪的漂移。那么，既然加计是参考值，为什么不能直接置信于加计呢？这里就扯到互补的思想了，加计并不是稳定的，是一直震荡的，不平滑，但值是没有漂移的，积分不会产生大的误差，这样也可以看做是，我们取了陀螺仪稳定的优点，又取了加计没有漂移的优点。

（7）更新四元数，并归一化

q0 += (-q1 * gyro.x - q2 * gyro.y - q3 * gyro.z) * halfT;
q1 += (q0 * gyro.x + q2 * gyro.z - q3 * gyro.y) * halfT;
q2 += (q0 * gyro.y - q1 * gyro.z + q3 * gyro.x) * halfT;
q3 += (q0 * gyro.z + q1 * gyro.y - q2 * gyro.x) * halfT;

normalise = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3);
q0 *= normalise;
q1 *= normalise;
q2 *= normalise;
q3 *= normalise;

这里在解释一下四元数更新的算法，这个实际上就是对四元数运动学方程套用龙格库塔方法，这里的计算过程就直接搬运了，没什么好说的。

（8）解算欧拉角

这里就是之前说的欧拉角与四元数的对应关系。

state->attitude.pitch = -asinf(vecxZ) * RAD2DEG; 
state->attitude.roll = atan2f(vecyZ, veczZ) * RAD2DEG;
state->attitude.yaw = atan2f(2 * (q1 * q2 + q0 * q3),q0s + q1s - q2s - q3s) * RAD2DEG;

2.串级PID控制

PID控制器的设计是基于控制模型的，在前面说过，我们设计的PID控制如下，

①姿态环

$\large \\ e_{\Theta }= \Theta _{f}-\Theta _{r} \\ \omega_{d}=K_{\Theta p}e_{\Theta }+K_{\Theta i}\int e_{\Theta }+K_{\Theta d}\dot{e_{\Theta }} \\e_{\omega }=\omega -\omega _{d}\\ \tau _{d}=K_{\omega p}e_{\omega }+K_{\omega i}\int e_{\omega }+K_{\omega d}\dot{e}_{\omega }$

void attitudeRatePID(Axis3f *actualRate,attitude_t *desiredRate,control_t *output)	
{
	output->roll = pidOutLimit(pidUpdate(&pidRateRoll, desiredRate->roll - actualRate->x));
	output->pitch = pidOutLimit(pidUpdate(&pidRatePitch, desiredRate->pitch - actualRate->y));
	output->yaw = pidOutLimit(pidUpdate(&pidRateYaw, desiredRate->yaw - actualRate->z));
}

void attitudeAnglePID(attitude_t *actualAngle,attitude_t *desiredAngle,attitude_t *outDesiredRate)	
{
	outDesiredRate->roll = pidUpdate(&pidAngleRoll, desiredAngle->roll - actualAngle->roll);
	outDesiredRate->pitch = pidUpdate(&pidAnglePitch, desiredAngle->pitch - actualAngle->pitch);

	float yawError = desiredAngle->yaw - actualAngle->yaw ;
	if (yawError > 180.0f) 
		yawError -= 360.0f;
	else if (yawError < -180.0) 
		yawError += 360.0f;
	outDesiredRate->yaw = pidUpdate(&pidAngleYaw, yawError);
}

姿态环，代码实现的时候还要加入饱和，另外，遥控器模式时，实际是控制yaw的的角速率，直接用单环速率控制。

②高度环

$\large \\ e_{P_{z} }= P_{zf}-P _{zr} \\v_{z}_{d}=K_{P_{z}}e_{P_{z}}\\e_{v_{z}}=v_{z} -v_{z}_{d}\\ f _{d}=K_{v_{z} p}e_{v_{z} }+K_{v_{z} i}\int e_{v_{z} }+K_{\omega d}\dot{e}_{v_{z} }$

void altholdPID(float* thrust, const state_t *state, const setpoint_t *setpoint)
{
	float newThrust = 0.0;	
	
	newThrust = THRUST_SCALE * runPidZ(&posPid.pidVZ, state->position.z, setpoint, POS_UPDATE_DT);
	
	if(getCommanderKeyFlight())
		detecWeight(*thrust, newThrust, state->velocity.z);
	
	*thrust = newThrust + posPid.thrustBase;
	
	if (*thrust > 60000) 
	{
		*thrust = 60000;
	}	
}

static float runPidZ(pidAxis_t *axis, float input, const setpoint_t *setpoint, float dt) 
{
	float out = 0.f;
	if (axis->preMode == false && setpoint->isAltHold == true)
	{
		positionResetAllPID();
		axis->setpoint = input + START_HIRHT;
		posPid.thrustBase = limitThrustBase(configParam.thrustBase);
	}
	axis->preMode = setpoint->isAltHold;

	if(setpoint->isAltHold == true)
	{
		axis->setpoint += setpoint->velocity.z * dt;
		out = pidUpdate(&axis->pid, axis->setpoint - input);
	}
	return out;
}

这里minifly高度环实际也是单环。

pid更新的代码，

float pidUpdate(PidObject* pid, const float error)
{
	float output;

	pid->error = error;   

	pid->integ += pid->error * pid->dt;
	if (pid->integ > pid->iLimit)
	{
		pid->integ = pid->iLimit;
	}
	else if (pid->integ < pid->iLimitLow)
	{
		pid->integ = pid->iLimitLow;
	}

	pid->deriv = (pid->error - pid->prevError) / pid->dt;

	pid->outP = pid->kp * pid->error;
	pid->outI = pid->ki * pid->integ;
	pid->outD = pid->kd * pid->deriv;

	output = pid->outP + pid->outI + pid->outD;

	pid->prevError = pid->error;

	return output;
}

pid算法虽然都是一样的，但是基于pid控制器，不同飞控实现的方式也不太一样，这里不过多解读minifly的飞控了，后面好好学学px4的源码。

3.控制分配

传统四旋翼中，控制分配算法很简单，因为伪控制量和实际控制量的个数是相同的，编号好电机之后，相应正负，分配给电机即可。

void powerControl(control_t *control)
{
	s16 r = control->roll / 2.0f;
	s16 p = control->pitch / 2.0f;
	
	motorPWM.m1 = limitThrust(control->thrust - r - p + control->yaw);
	motorPWM.m2 = limitThrust(control->thrust - r + p - control->yaw);
	motorPWM.m3 = limitThrust(control->thrust + r + p + control->yaw);
	motorPWM.m4 = limitThrust(control->thrust + r - p - control->yaw);	
}

传统四旋翼的控制量是四个，在一个三维控制内，自由度有六个，这样的控制就是欠驱动的。如果我的伪控制量有六个，实际控制量也有六个，那我可以实现三维空间内的解耦控制。如果我的伪控制量有六个，实际控制量大于六个，且这六个控制量可以实现对，六个伪控制量做的事情。后面两个种情况控制分配就很重要了，包括六轴啊这种，四个伪控制量，六个实际控制量，也需要合理的控制分配。关于控制分配呢，需要思考的还很多，在这里不多说了。

结语：总之呢，关于四旋翼涉及的面太广了，这里只是把大致框架整理了一下，其实实现四旋翼控制的方法有很多，这里都是最简单的，像水平环的控制，解算时其他一些传感器的融合啊等等都还没说，一些更深入的东西也还没太研究明白，后面继续研究……

本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容，请联系:hwhale#tublm.com(使用前将#替换为@)