在介绍变分之前,首先回顾微分的定义:
当自变量 x → x + d x x\rightarrow x+\mathrm{d}x x→x+dx 时,相应的因变量 y → y + d y y\rightarrow y+\mathrm{d}y y→y+dy。
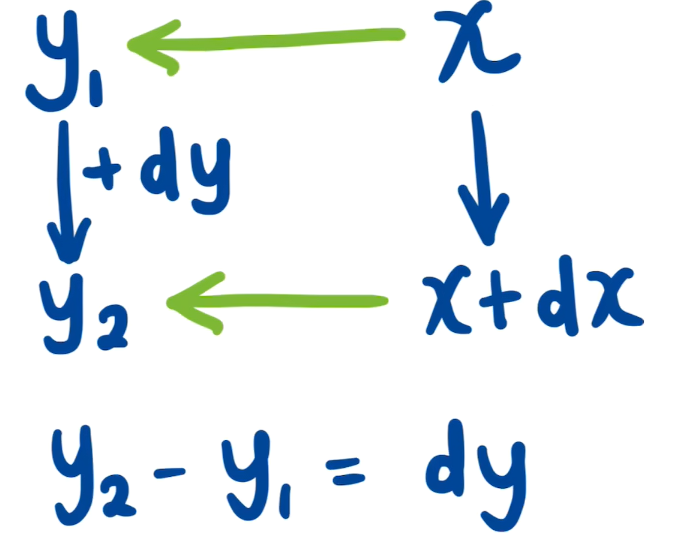
则此时 d y \mathrm{d}y dy 就是函数 y ( x ) y(x) y(x) 的微分了。下面为上述过程的图示:

泛函为函数的函数,

通过上面的介绍,那么问题来了,如何用同样的思路去研究泛函的变化?通过类比推广, x x x 的变化,可以推广为函数的变形:
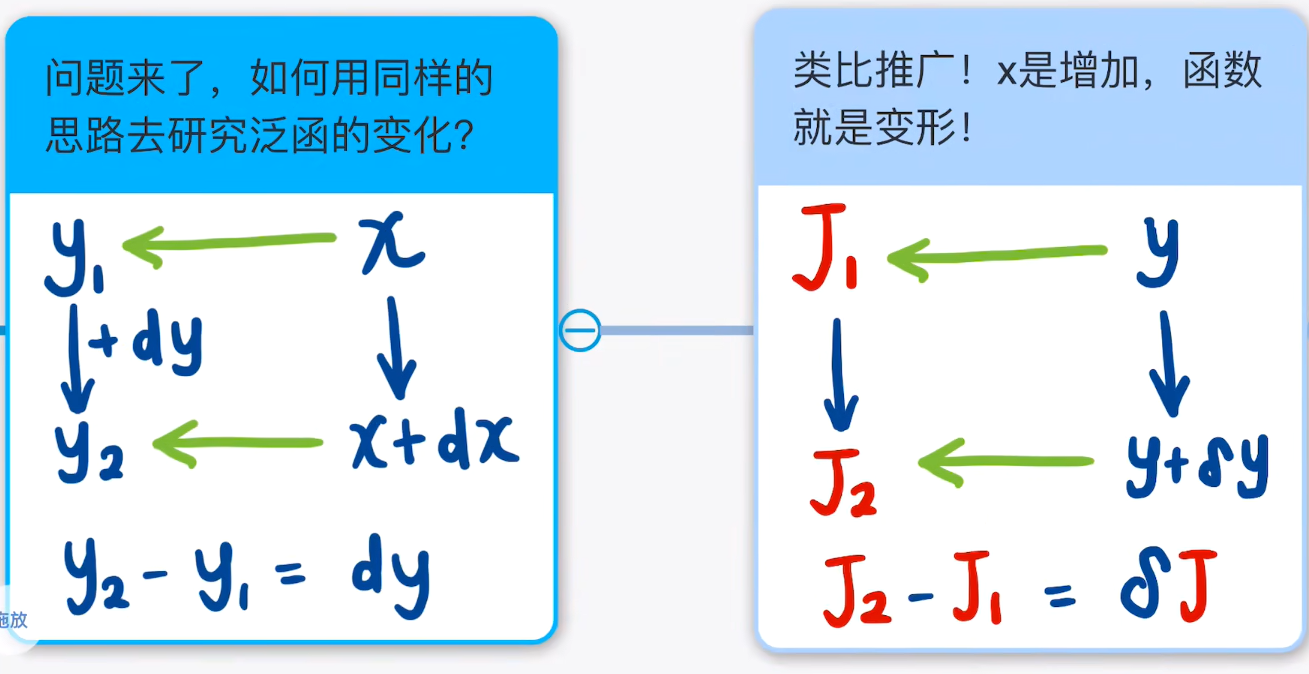
那么函数的变形如何理解呢?如下图:
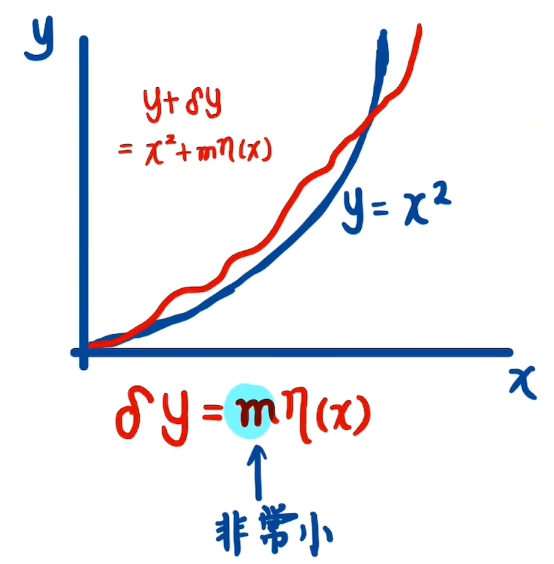
我们可以把原先的函数作一点点形变,即可以在原先的函数上加上一个任意函数 η ( x ) \eta(x) η(x),然后在任意函数的前面乘上非常小或者足够小的系数 m m m,此时我们就可以把 y = x 2 y=x^{2} y=x2(仅举例,可以推广)和新函数 y + δ y = x 2 + m η ( x ) y+\mathtt{\delta} y=x^{2}+m\eta(x) y+δy=x2+mη(x) 的差导致的泛函 J J J 的变化 J 2 − J 1 = δ J J_{2}-J_{1}=\delta J J2−J1=δJ 就是泛函 J J J 的变分。
这个泛函的变分的线性化表示是整个变分中最重要的一步!同理,在微积分中,使用线性化的思想处理问题也是处理所有其他问题的前提!
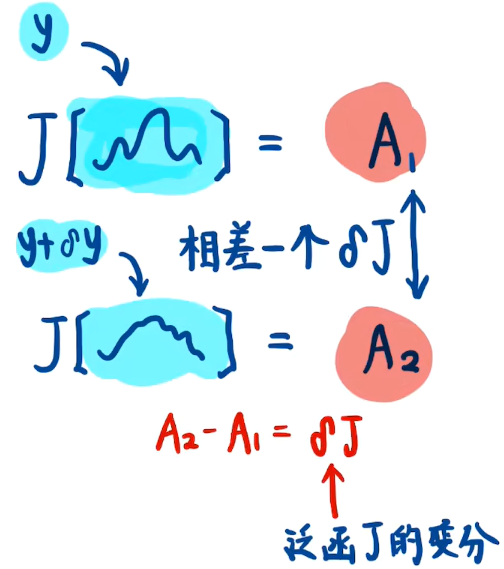
下面是泛函变分的示意图:
变分和微分的运算法则在很多情况下都是相同的,可以直接把微分的运算法则拿过来用就可以了:
d y ( x ) = y ′ ( x ) d x ⇓ δ y ( x ) = y ′ ( x ) δ x \mathrm{d}y(x)=y'(x)\mathrm{d}x\\ \Downarrow\\ \delta y(x)=y'(x)\delta x dy(x)=y′(x)dx⇓δy(x)=y′(x)δx
d ( A B ) = B d A + A d B ⇓ δ ( A B ) = B δ A + A δ B \mathrm{d}(AB)=B\mathrm{d}A+A\mathrm{d}B\\ \Downarrow\\ \delta (AB)=B\delta A+A\delta B\\ d(AB)=BdA+AdB⇓δ(AB)=BδA+AδB
d Z = ∂ Z ∂ x d x + ∂ Z ∂ y d y ⇓ δ Z = ∂ Z ∂ x δ x + ∂ Z ∂ y δ y \mathrm{d} Z=\frac{\partial Z}{\partial x}\mathrm{d} x+\frac{\partial Z}{\partial y}\mathrm{d} y\\ \Downarrow\\ \delta Z=\frac{\partial Z}{\partial x}\delta x+\frac{\partial Z}{\partial y}\delta y dZ=∂x∂Zdx+∂y∂Zdy⇓δZ=∂x∂Zδx+∂y∂Zδy


变分微积分,或变分法(Calculus of Variations or variational method)是一个数学分析领域,它使用变分(函数和泛函的微小变化)来找到泛函的最大值和最小值:从一组函数到实数的映射。泛函通常表示为涉及函数及其导数的定积分。使用变分法的欧拉-拉格朗日方程可以找到最大化或最小化泛函的函数。
变分法是 17 世纪末发展起来的一门数学分支,是处理泛函的数学领域,和处理数的函数的普通微积分相对。它最终寻求的是极值函数:它们使得泛函取得极大或极小值。变分法起源于一些具体的物理学问题,最终由数学家研究解决。有些曲线上的经典问题采用这种形式表达:一个例子是最速降线,在重力作用下一个粒子沿着该路径可以在最短时间从点 A 到达不直接在它底下的一点 B。在所有从 A 到 B 的曲线中,必须极小化代表下降时间的表达式。
另外还有找到连接两点的最短长度曲线。如果没有约束,则解是点之间的直线。但是,如果曲线被限制在空间表面上,那么解决方案就不太明显,并且可能存在许多解决方案。这种解决方案被称为测地线。费马原理提出了一个相关问题:光遵循连接两点的最短光程路径,这取决于介质的材料。力学中一个对应的概念是最小/静止作用原理。
可以说变分法始于 1687 年牛顿的最小阻力问题,随后是约翰·伯努利 (Johann Bernoulli)(1696 年)提出的短时线问题。它立即引起了雅各布·伯努利(Jakob Bernoulli)和 Marquis de l’Hôpital 的注意,但莱昂哈德·欧拉(Leonhard Euler)从 1733 年开始首先阐述了这个主题。拉格朗日受到欧拉工作的影响,对这一理论做出了重大贡献。在欧拉看到 19 岁的拉格朗日 1755 年的作品后,欧拉放弃了他自己的部分几何方法,转而支持拉格朗日的纯分析方法,并在他 1756 年的讲座 “Elementa Calculi Variationum” 中将这个主题重新命名为变分法。
勒让德 (Legendre) (1786) 制定了一种方法,但并不完全令人满意,用于区分最大值和最小值。艾萨克·牛顿和戈特弗里德·莱布尼茨也对这个主题给予了一些早期的关注。在这其中,文森佐·布鲁纳奇 (Vincenzo Brunacci) (1810)、卡尔·弗里德里希·高斯 (Carl Friedrich Gauss) (1829)、西蒙·泊松 (Siméon Poisson) (1831)、米哈伊尔·奥斯特罗格拉茨基 (Mikhail Ostrogradsky) (1834) 和卡尔·雅可比 (Carl Jacobi) (1837) 都是贡献者。 Sarrus (1842) 的一项重要的综合性工作是由 Cauchy (1844) 浓缩和改进的。 Strauch (1849)、Jellett (1850)、Otto Hesse (1857)、Alfred Clebsch (1858) 和 Lewis Buffett Carll (1885) 撰写了其他有价值的论文和回忆录,但也许本世纪最重要的著作是维尔斯特拉斯(Weierstrass)。他著名的理论课程是划时代的,可以说他是第一个将其建立在坚实和不容置疑的基础上的人。1900 年发表的第 20 和第 23 希尔伯特问题鼓励了进一步的发展。
在 20 世纪,David Hilbert、Oskar Bolza、Gilbert Ames Bliss、Emmy Noether、Leonida Tonelli、Henri Lebesgue 和 Jacques Hadamard 等做出了重大贡献。Marston Morse 在现在所谓的 Morse 理论中应用了变分法。Lev Pontryagin、Ralph Rockafellar 和 F. H. Clarke 为最优控制理论中的变分微积分开发了新的数学工具。Richard Bellman 的动态规划是变分法的替代方法。
变分法与泛函的最大值或最小值(统称为极值)有关。泛函将函数映射到标量,因此泛函被描述为“函数的函数”。泛函对于定义在给定域上的给定函数空间的元素 y y y 具有极值。一个泛函 J [ y ] J[y] J[y] 如果 Δ J = J [ y ] − J [ f ] \Delta J=J[y]-J[f] ΔJ=J[y]−J[f] 对于 f f f 的任意小的邻域中的所有 y y y 具有相同的符号。函数 f f f 称为极值函数或极值。如果在 f f f 的任意小邻域中处处 Δ J ≤ 0 \Delta J\leq 0 ΔJ≤0,则 J [ f ] J[f] J[f] 被称为局部极大值,相反,如果 Δ J ≥ 0 \Delta J\geq 0 ΔJ≥0,则称为局部极小值。对于连续函数的函数空间,对应的泛函的极值称为强极值或弱极值,这取决于连续函数的一阶导数是否都是连续的。
泛函的强极值和弱极值都是针对连续函数空间的,但强极值还有一个额外的要求,即空间中函数的一阶导数是连续的。因此,强极值也是弱极值,但反过来可能不成立。找到强极值比找到弱极值更难。用于寻找弱极值的必要条件的一个例子是欧拉-拉格朗日方程(Euler-Lagrange equation)。
在变分法中,泛函导数(或变分导数) 将泛函的变化与泛函所依赖的函数的变化联系起来。
在变分法中,泛函通常用函数、它们的参数和它们的导数的积分来表示。在泛函的积分 L L L 中,如果函数 f f f 通过添加另一个任意小的函数 δ f \delta f δf 来改变,并且所得被积函数以 δ f \delta f δf 的幂展开,则一阶项中 δ f \delta f δf 的系数称为泛函导数。
例如,考虑泛函:
J [ f ] = ∫ a b L ( x , f ( x ) , f ′ ( x ) ) d x J[f]=\int _{a}^{b}L(x,f(x),f'(x)\,)\,\mathrm{d}x J[f]=∫abL(x,f(x),f′(x))dx
其中 f ′ ( x ) ≡ d f / d x f'(x)\equiv\mathrm{d}f/\mathrm{d}x f′(x)≡df/dx。如果通过向其添加函数 δ f \delta f δf 来改变 f f f(注意此时 x x x 相对不变),并且将得到的被积函数 L ( x , f + δ f , f ′ + δ f ′ ) L(x,f+\delta f,f'+\delta f') L(x,f+δf,f′+δf′) 以 δ f \delta f δf 的幂展开,则 J J J 的值在 δ f \delta f δf 中的一阶变化可表示为:
δ J = ∫ a b ( ∂ L ∂ f δ f ( x ) + ∂ L ∂ f ′ d d x δ f ( x ) ) d x = ∫ a b ( ∂ L ∂ f − d d x ∂ L ∂ f ′ ) δ f ( x ) d x + ∂ L ∂ f ′ ( b ) δ f ( b ) − ∂ L ∂ f ′ ( a ) δ f ( a ) \begin{aligned} \delta J &=\int _{a}^{b}\left({\frac {\partial L}{\partial f}}\delta f(x)+{\frac {\partial L}{ \partial f'}}{\frac {\mathrm{d}}{\mathrm{d}x}}\delta f(x)\right)\,\mathrm{d}x\\ &=\int _{a}^{b}\left({\frac {\partial L}{\partial f}}-{\frac {\mathrm{d}}{\mathrm{d}x}}{\frac {\partial L}{\partial f'}}\right)\delta f(x)\,\mathrm{d}x\,+\,{\frac {\partial L}{\partial f'}}(b)\delta f(b)\,-\,{\frac {\partial L}{\partial f'}}(a)\delta f(a) \end{aligned} δJ=∫ab(∂f∂Lδf(x)+∂f′∂Ldxdδf(x))dx=∫ab(∂f∂L−dxd∂f′∂L)δf(x)dx+∂f′∂L(b)δf(b)−∂f′∂L(a)δf(a)
其中导数的变分, δ f ′ \delta f' δf′ 被重写为变分的导数 ( δ f ) ′ (\delta f)' (δf)′,即:
δ f ′ = f 2 , ′ − f 1 , ′ = ( f 2 , 2 − f 2 , 1 d x ) − ( f 1 , 2 − f 1 , 1 d x ) = ( f 2 , 2 − f 1 , 2 d x ) − ( f 2 , 1 − f 1 , 1 d x ) = ( δ f , 2 d x ) − ( δ f , 1 d x ) = ( δ f , 2 − δ f , 1 d x ) = ( δ f ) ′ = d d x δ f ( x ) \begin{aligned} \delta f' &=f'_{2,}-f'_{1,}\\ &=(\frac{f_{2,2}-f_{2,1}}{\mathrm{d} x})-(\frac{f_{1,2}-f_{1,1}}{\mathrm{d} x})\\ &=(\frac{f_{2,2}-f_{1,2}}{\mathrm{d} x})-(\frac{f_{2,1}-f_{1,1}}{\mathrm{d} x})\\ &=(\frac{\delta f_{,2}}{\mathrm{d} x})-(\frac{\delta f_{,1}}{\mathrm{d} x})\\ &=(\frac{\delta f_{,2}-\delta f_{,1}}{\mathrm{d} x})\\ &=(\delta f)'\\ &=\frac{\mathrm{d}}{\mathrm{d}x}\delta f(x) \end{aligned} δf′=f2,′−f1,′=(dxf2,2−f2,1)−(dxf1,2−f1,1)=(dxf2,2−f1,2)−(dxf2,1−f1,1)=(dxδf,2)−(dxδf,1)=(dxδf,2−δf,1)=(δf)′=dxdδf(x)
即利用了线性性质,其中第一个下标是变分对应的不同函数,第二个下标是同一函数下不同横坐标下的值。上述推导中使用了部分积分。
在本节中,定义了泛函导数(functional derivative)。然后根据泛函导数定义泛函微分(functional differential)。
给定表示(连续/平滑)函数 ρ \rho ρ(具有某些边界条件等)的流形 M M M,则一个泛函 F F F 可以定义为
F : M → R or F : M → C F\colon M\to \mathbb {R} \quad {\text{or}}\quad F\colon M\to \mathbb {C} F:M→RorF:M→C
F [ ρ ] F[\rho] F[ρ] 的泛函导数,表示为 δ F / δ ρ \delta F/\delta \rho δF/δρ,其定义为:
∫ δ F δ ρ ( x ) ϕ ( x ) d x = lim ε → 0 F [ ρ + ε ϕ ] − F [ ρ ] ε = [ d d ε F [ ρ + ε ϕ ] ] ε = 0 \begin{aligned} \int {\frac {\delta F}{\delta \rho }}(x)\phi (x)\;\mathrm{d}x&=\lim _{\varepsilon \to 0}{\frac {F[\rho +\varepsilon \phi ]-F[\rho ]}{\varepsilon }}\\&=\left[{\frac {\mathrm{d}}{\mathrm{d}\varepsilon }}F[\rho +\varepsilon \phi ]\right]_{\varepsilon =0} \end{aligned} ∫δρδF(x)ϕ(x)dx=ε→0limεF[ρ+εϕ]−F[ρ]=[dεdF[ρ+εϕ]]ε=0
其中 ϕ \phi ϕ 是一个任意函数。 ε ϕ \varepsilon \phi εϕ 称为 ρ \rho ρ 的变分(variation)。
换句话说:
ϕ ↦ [ d d ε F [ ρ + ε ϕ ] ] ε = 0 \phi \mapsto \left[{\frac {\mathrm{d}}{\mathrm{d}\varepsilon }}F[\rho +\varepsilon \phi ]\right]_{\varepsilon =0} ϕ↦[dεdF[ρ+εϕ]]ε=0
是一个线性泛函,因此可以应用 Riesz–Markov–Kakutani representation theorem 将该泛函表示为针对某种度量的积分。然后 δ F / δ ρ \delta F/\delta \rho δF/δρ 被定义为该度量的 Radon-Nikodym derivative。
我们认为函数 δ F / δ ρ \delta F/\delta \rho δF/δρ 是 F F F 在点 ρ \rho ρ 处的梯度(即,如果函数 ρ \rho ρ 在点 x x x 处改变(即 x x x 变化时, ρ \rho ρ 在变),泛函 F F F 将改变多少):
∫ δ F δ ρ ( x ) ϕ ( x ) d x \int {\frac {\delta F}{\delta \rho }}(x)\phi (x)\;\mathrm{d}x ∫δρδF(x)ϕ(x)dx
作为点 ρ \rho ρ 在 ϕ \phi ϕ 方向上的方向导数。类似于向量微积分, ϕ ( x ) \phi(x) ϕ(x) 与梯度 δ F / δ ρ \delta F/\delta\rho δF/δρ 的内积给出方向导数。
泛函 F [ ρ ] F\left[\rho \right] F[ρ] 的微分(或变分或一阶变分)为:
δ F [ ρ ; ϕ ] = ∫ δ F δ ρ ( x ) ϕ ( x ) d x \delta F[\rho ;\phi ]=\int {\frac {\delta F}{\delta \rho }}(x)\ \phi (x)\ \mathrm{d}x δF[ρ;ϕ]=∫δρδF(x) ϕ(x) dx
其中, ϕ \phi ϕ 是 ρ \rho ρ 的变化,所以我们“正式”有 ϕ = δ ρ \phi =\delta \rho ϕ=δρ,然后这在形式上类似于函数 F ( ρ 1 , ρ 2 , … , ρ n ) F(\rho _{1},\rho _{2},\dots ,\rho _{n}) F(ρ1,ρ2,…,ρn) 的全微分:
d F = ∑ i = 1 n ∂ F ∂ ρ i d ρ i \mathrm{d}F=\sum _{i=1}^{n}{\frac {\partial F}{\partial \rho _{i}}}\ \mathrm{d}\rho _{i} dF=i=1∑n∂ρi∂F dρi
其中 ρ 1 , ρ 2 , … , ρ n \rho _{1},\rho _{2},\dots ,\rho _{n} ρ1,ρ2,…,ρn 是自变量。比较最后两个方程,泛函导数 δ F / δ ρ ( x ) \delta F/\delta \rho (x) δF/δρ(x) 的作用类似于偏导数 ∂ F / ∂ ρ i \partial F/\partial \rho _{i} ∂F/∂ρi,其中积分变量 x x x 类似于求和下标 i i i。
与函数的导数一样,泛函导数满足以下性质,其中 F [ ρ ] F[\rho] F[ρ] 和 G [ ρ ] G[\rho] G[ρ] 是泛函(注意 δ F δ ρ ( x ) ≡ δ F δ ρ ( x ) \frac{\delta F}{\delta \rho}(x)\equiv\frac{\delta F}{\delta \rho(x)} δρδF(x)≡δρ(x)δF):
δ ( λ F + μ G ) [ ρ ] δ ρ ( x ) = λ δ F [ ρ ] δ ρ ( x ) + μ δ G [ ρ ] δ ρ ( x ) {\frac {\delta (\lambda F+\mu G)[\rho ]}{\delta \rho (x)}}=\lambda {\frac {\delta F[\rho ]}{\delta \rho (x)}}+\mu {\frac {\delta G[\rho ]}{\delta \rho (x)}} δρ(x)δ(λF+μG)[ρ]=λδρ(x)δF[ρ]+μδρ(x)δG[ρ]
其中 λ \lambda λ, μ \mu μ 是常数。
δ ( F G ) [ ρ ] δ ρ ( x ) = δ F [ ρ ] δ ρ ( x ) G [ ρ ] + F [ ρ ] δ G [ ρ ] δ ρ ( x ) {\frac {\delta (FG)[\rho ]}{\delta \rho (x)}}={\frac {\delta F[\rho ]}{\delta \rho (x)}} G[\rho ]+F[\rho ]{\frac {\delta G[\rho ]}{\delta \rho (x)}} δρ(x)δ(FG)[ρ]=δρ(x)δF[ρ]G[ρ]+F[ρ]δρ(x)δG[ρ]
δ F [ G [ ρ ] ] δ ρ ( y ) = ∫ d x δ F [ G ] δ G ( x ) G = G [ ρ ] ⋅ δ G [ ρ ] ( x ) δ ρ ( y ) {\frac {\delta F[G[\rho ]]}{\delta \rho (y)}}=\int \mathrm{d}x{\frac {\delta F[G]}{\delta G(x) }}_{G=G[\rho ]}\cdot {\frac {\delta G[\rho ](x)}{\delta \rho (y)}} δρ(y)δF[G[ρ]]=∫dxδG(x)δF[G]G=G[ρ]⋅δρ(y)δG[ρ](x)
δ F [ g ( ρ ) ] δ ρ ( y ) = δ F [ g ( ρ ) ] δ g [ ρ ( y ) ] d g ( ρ ) d ρ ( y ) {\frac {\delta F[g(\rho )]}{\delta \rho (y)}}={\frac {\delta F[g(\rho )]}{\delta g[\rho (y)]}}\ {\frac {\mathrm{d}g(\rho )}{\mathrm{d}\rho (y)}} δρ(y)δF[g(ρ)]=δg[ρ(y)]δF[g(ρ)] dρ(y)dg(ρ)
确定一类常见泛函的泛函导数(functional derivatives)的公式,可以写成函数及其导数的积分。这是欧拉-拉格朗日方程的推广:实际上,泛函导数是在从拉格朗日力学(18 世纪)的最小作用原理推导第二类拉格朗日方程的过程中引入的。下面的前三个例子来自密度泛函理论(20 世纪),第四个例子来自统计力学(19 世纪)。
给定一个泛函
F [ ρ ] = ∫ f ( r , ρ ( r ) , ∇ ρ ( r ) ) d r {\displaystyle F[\rho ]=\int f({\boldsymbol {r}},\rho ({\boldsymbol {r}}),\nabla \rho ({\boldsymbol {r}}))\,\mathrm{d} {\boldsymbol {r}}} F[ρ]=∫f(r,ρ(r),∇ρ(r))dr
和一个在积分区域边界上消失的函数 ϕ ( r \phi(\boldsymbol{r} ϕ(r),后者来自上一节的定义,
∫ δ F δ ρ ( r ) ϕ ( r ) d r = [ d d ε ∫ f ( r , ρ + ε ϕ , ∇ ρ + ε ∇ ϕ ) d r ] ε = 0 = ∫ ( ∂ f ∂ ρ ϕ + ∂ f ∂ ∇ ρ ⋅ ∇ ϕ ) d r = ∫ [ ∂ f ∂ ρ ϕ + ∇ ⋅ ( ∂ f ∂ ∇ ρ ϕ ) − ( ∇ ⋅ ∂ f ∂ ∇ ρ ) ϕ ] d r = ∫ [ ∂ f ∂ ρ ϕ − ( ∇ ⋅ ∂ f ∂ ∇ ρ ) ϕ ] d r = ∫ ( ∂ f ∂ ρ − ∇ ⋅ ∂ f ∂ ∇ ρ ) ϕ ( r ) d r {\displaystyle {\begin{aligned}\int {\frac {\delta F}{\delta \rho ({\boldsymbol {r}})}}\,\phi ({\boldsymbol {r}})\,\mathrm{d}{\boldsymbol {r}}&=\left[{\frac {\mathrm{d}}{\mathrm{d}\varepsilon }}\int f({\boldsymbol {r}},\rho +\varepsilon \phi ,\nabla \rho +\varepsilon \nabla \phi )\,\mathrm{d}{\boldsymbol {r}}\right]_{\varepsilon =0}\\&=\int \left({\frac {\partial f}{\partial \rho }}\,\phi +{\frac {\partial f}{\partial \nabla \rho }}\cdot \nabla \phi \right)\mathrm{d}{\boldsymbol {r}}\\&=\int \left[{\frac {\partial f}{\partial \rho }}\,\phi +\nabla \cdot \left({\frac {\partial f}{\partial \nabla \rho }}\,\phi \right)-\left(\nabla \cdot {\frac {\partial f}{\partial \nabla \rho }}\right)\phi \right]\mathrm{d}{\boldsymbol {r}}\\&=\int \left[{\frac {\partial f}{\partial \rho }}\,\phi -\left(\nabla \cdot {\frac {\partial f}{\partial \nabla \rho }}\right)\phi \right]\mathrm{d}{\boldsymbol {r}}\\&=\int \left({\frac {\partial f}{\partial \rho }}-\nabla \cdot {\frac {\partial f}{\partial \nabla \rho }}\right)\phi ({\boldsymbol {r}})\ \mathrm{d}{\boldsymbol {r}}\,\end{aligned}}} ∫δρ(r)δFϕ(r)dr=[dεd∫f(r,ρ+εϕ,∇ρ+ε∇ϕ)dr]ε=0=∫(∂ρ∂fϕ+∂∇ρ∂f⋅∇ϕ)dr=∫[∂ρ∂fϕ+∇⋅(∂∇ρ∂fϕ)−(∇⋅∂∇ρ∂f)ϕ]dr=∫[∂ρ∂fϕ−(∇⋅∂∇ρ∂f)ϕ]dr=∫(∂ρ∂f−∇⋅∂∇ρ∂f)ϕ(r) dr
第二行是使用全导数获得的,其中 ∂ f / ∂ ∇ ρ \partial f /\partial \nabla\rho ∂f/∂∇ρ 是标量相对于向量的导数,在三维笛卡尔坐标系中:
∂ f ∂ ∇ ρ = ∂ f ∂ ρ x i ^ + ∂ f ∂ ρ y j ^ + ∂ f ∂ ρ z k ^ \frac{\partial f}{\partial\nabla\rho}=\frac{\partial f}{\partial \rho_{x}}\boldsymbol{\hat{i}}+\frac{\partial f}{\partial \rho_{y}}\boldsymbol{\hat{j}}+\frac{\partial f}{\partial \rho_{z}}\boldsymbol{\hat{k}} ∂∇ρ∂f=∂ρx∂fi^+∂ρy∂fj^+∂ρz∂fk^
其中 ρ x = ∂ ρ ∂ x \rho_{x}=\frac{\partial\rho}{\partial x} ρx=∂x∂ρ, ρ y = ∂ ρ ∂ y \rho_{y}=\frac{\partial\rho}{\partial y} ρy=∂y∂ρ, ρ z = ∂ ρ ∂ z \rho_{z}=\frac{\partial\rho}{\partial z} ρz=∂z∂ρ, i ^ \boldsymbol{\hat{i}} i^, j ^ \boldsymbol{\hat{j}} j^, k ^ \boldsymbol{\hat{k}} k^ 是沿 x x x, y y y, z z z 轴的单位向量。
第三行是通过使用散度的乘积规则获得的:
∇ ⋅ ( φ F ) = ( ∇ φ ) ⋅ F + φ ( ∇ ⋅ F ) {\displaystyle \nabla \cdot (\varphi \mathbf {F} )=(\nabla \varphi )\cdot \mathbf {F} +\varphi (\nabla \cdot \mathbf {F} )} ∇⋅(φF)=(∇φ)⋅F+φ(∇⋅F)
第四行是使用散度定理(Divergence theorem)和积分区域边界上 ϕ = 0 \phi = 0 ϕ=0 的条件获得的:
∫ ( ∇ ⋅ F ) d r = ∭ V ( ∇ ⋅ F ) d V = ∯ S ( F ⋅ n ^ ) d S \int (\nabla\cdot\mathbf{F})\mathrm{d}\boldsymbol{r}=\iiint_{V}(\nabla\cdot\mathbf{F})\mathrm{d}V=\oiint_{S}(\mathbf{F}\cdot\hat{\mathbf{n}})\mathrm{d}S ∫(∇⋅F)dr=∭V(∇⋅F)dV=∬ S(F⋅n^)dS
所以:
∫ ∇ ⋅ ( ∂ f ∂ ∇ ρ ϕ ) d r = ∭ V ∇ ⋅ ( ∂ f ∂ ∇ ρ ϕ ) d V = ∯ S ∂ f ∂ ∇ ρ ϕ d S = 0 \int\nabla \cdot \left({\frac {\partial f}{\partial \nabla \rho }}\,\phi \right)\mathrm{d}\boldsymbol{r}=\iiint_{V}\nabla \cdot \left({\frac {\partial f}{\partial \nabla \rho }}\,\phi \right)\mathrm{d}V=\oiint_{S}{\frac {\partial f}{\partial \nabla \rho }}\,\phi \mathrm{d}\boldsymbol{S}=0 ∫∇⋅(∂∇ρ∂fϕ)dr=∭V∇⋅(∂∇ρ∂fϕ)dV=∬ S∂∇ρ∂fϕdS=0
由于 ϕ \phi ϕ 也是一个任意函数,将 fundamental lemma of calculus of variations 应用于最后一行,泛函导数为
δ F δ ρ ( r ) = ∂ f ∂ ρ − ∇ ⋅ ∂ f ∂ ∇ ρ {\displaystyle {\frac {\delta F}{\delta \rho ({\boldsymbol {r}})}}={\frac {\partial f}{\partial \rho }}-\nabla \cdot {\frac {\partial f}{\partial \nabla \rho }}} δρ(r)δF=∂ρ∂f−∇⋅∂∇ρ∂f
其中 ρ = ρ ( r ) \rho = \rho(\boldsymbol{r}) ρ=ρ(r) 和 f = f ( r , ρ , ∇ ρ ) f = f (\boldsymbol{r}, \rho, \nabla\rho) f=f(r,ρ,∇ρ)。该公式适用于本节开头 F [ ρ ] F[\rho] F[ρ] 给出的函数形式的情况。对于其他泛函形式,泛函导数的定义可以作为其确定的起点。(参见 Coulomb potential energy functional 示例。)
上面的泛函导数方程可以推广到包括高维和高阶导数的情况。泛函将是,
F [ ρ ( r ) ] = ∫ f ( r , ρ ( r ) , ∇ ρ ( r ) , ∇ ( 2 ) ρ ( r ) , … , ∇ ( N ) ρ ( r ) ) d r {\displaystyle F[\rho ({\boldsymbol {r}})]=\int f({\boldsymbol {r}},\rho ({\boldsymbol {r}}),\nabla \rho ({\boldsymbol {r}}),\nabla ^{(2)}\rho ({\boldsymbol {r}}),\dots ,\nabla ^{(N)}\rho ({\boldsymbol {r}}))\ \mathrm{d}{\boldsymbol {r}}} F[ρ(r)]=∫f(r,ρ(r),∇ρ(r),∇(2)ρ(r),…,∇(N)ρ(r)) dr
其中向量 r ∈ R n r\in \mathbf{R}^{n} r∈Rn, ∇ ( i ) \nabla^{(i)} ∇(i) 是一个张量,其 n i n^{i} ni 分量是 i i i 阶偏导算子,
[ ∇ ( i ) ] α 1 α 2 ⋯ α i = ∂ i ∂ r α 1 ∂ r α 2 ⋯ ∂ r α i where α 1 , α 2 , ⋯ , α i = 1 , 2 , ⋯ , n . {\displaystyle \left[\nabla ^{ (i)}\right]_{\alpha _{1}\alpha _{2}\cdots \alpha _{i}}={\frac {\partial ^{\,i}}{\partial r_{\alpha _{1}}\partial r_{\alpha _{2}}\cdots \partial r_{\alpha _{i}}}}\qquad \qquad {\text{where}}\quad \alpha _{1 },\alpha _{2},\cdots ,\alpha _{i}=1,2,\cdots ,n\ .} [∇(i)]α1α2⋯αi=∂rα1∂rα2⋯∂rαi∂iwhereα1,α2,⋯,αi=1,2,⋯,n .
比如,对于三维( n = 3 n=3 n=3),二阶导数( i = 2 i=2 i=2),张量 ∇ 2 \nabla^{2} ∇2 的基本元素为:
[ ∇ ( 2 ) ] α β = ∂ 2 ∂ r α ∂ r β where α , β = 1 , 2 , 3 {\displaystyle \left[\nabla ^{(2)}\right]_{\alpha \beta }={\frac {\partial ^{\,2}}{\partial r_{\alpha }\,\partial r_{\beta }}}\qquad \qquad {\text{where}}\quad \alpha ,\beta =1,2,3\,} [∇(2)]αβ=∂rα∂rβ∂2whereα,β=1,2,3
泛函导数定义的类似应用
δ F [ ρ ] δ ρ = ∂ f ∂ ρ − ∇ ⋅ ∂ f ∂ ( ∇ ρ ) + ∇ ( 2 ) ⋅ ∂ f ∂ ( ∇ ( 2 ) ρ ) + ⋯ + ( − 1 ) N ∇ ( N ) ⋅ ∂ f ∂ ( ∇ ( N ) ρ ) = ∂ f ∂ ρ + ∑ i = 1 N ( − 1 ) i ∇ ( i ) ⋅ ∂ f ∂ ( ∇ ( i ) ρ ) {\displaystyle {\begin{aligned}{\frac {\delta F[\rho ]}{\delta \rho }}&{}={\frac {\partial f}{\partial \rho }}-\nabla \cdot {\frac {\partial f}{\partial (\nabla \rho )}}+\nabla ^{(2)}\cdot {\frac {\partial f}{\partial \left(\nabla ^{(2)}\rho \right)}}+\dots +(-1)^{N}\nabla ^{(N)}\cdot {\frac {\partial f}{\partial \left(\nabla ^{(N)}\rho \right)}}\\&{}={\frac {\partial f}{\partial \rho }}+\sum _{i=1}^{N}(-1)^{i}\nabla ^{(i)}\cdot {\frac {\partial f}{\partial \left(\nabla ^{(i)}\rho \right)}}\ \end{aligned}}} δρδF[ρ]=∂ρ∂f−∇⋅∂(∇ρ)∂f+∇(2)⋅∂(∇(2)ρ)∂f+⋯+(−1)N∇(N)⋅∂(∇(N)ρ)∂f=∂ρ∂f+i=1∑N(−1)i∇(i)⋅∂(∇(i)ρ)∂f
在最后两个方程中,张量 ∂ f ∂ ( ∇ ( i ) ρ ) \frac {\partial f}{\partial \left(\nabla ^{(i)}\rho \right)} ∂(∇(i)ρ)∂f 的 n i n^{i} ni 元素是 f f f 关于 ρ \rho ρ 的偏导数的偏导数,
[ ∂ f ∂ ( ∇ ( i ) ρ ) ] α 1 α 2 ⋯ α i = ∂ f ∂ ρ α 1 α 2 ⋯ α i where ρ α 1 α 2 ⋯ α i ≡ ∂ i ρ ∂ r α 1 ∂ r α 2 ⋯ ∂ r α i {\displaystyle \left[{\frac {\partial f}{\partial \left(\nabla ^{(i)}\rho \right)}}\right]_{\alpha _{1}\alpha _{2}\cdots \alpha _{i}}={\frac {\partial f}{\partial \rho _{\alpha _{1}\alpha _{2}\cdots \alpha _{i}}}}\qquad \qquad {\text{where}}\quad \rho _{\alpha _{1}\alpha _{2}\cdots \alpha _{i}}\equiv {\frac {\partial ^{\,i}\rho }{\partial r_{\alpha _{1}}\,\partial r_{\alpha _{2}}\cdots \partial r_{\alpha _{i}}}}\ } [∂(∇(i)ρ)∂f]α1α2⋯αi=∂ρα1α2⋯αi∂fwhereρα1α2⋯αi≡∂rα1∂rα2⋯∂rαi∂iρ
张量标量积是:
∇ ( i ) ⋅ ∂ f ∂ ( ∇ ( i ) ρ ) = ∑ α 1 , α 2 , ⋯ , α i = 1 n ∂ i ∂ r α 1 ∂ r α 2 ⋯ ∂ r α i ∂ f ∂ ρ α 1 α 2 ⋯ α i {\displaystyle \nabla ^{(i)}\cdot {\frac {\partial f}{\partial \left(\nabla ^{(i)}\rho \right)}}=\sum _{\alpha _{1},\alpha _{2},\cdots ,\alpha _{i}=1}^{n}\ {\frac {\partial ^{\,i}}{\partial r_{\alpha _{1}}\,\partial r_{\alpha _{2}}\cdots \partial r_{\alpha _{i}}}}\ {\frac {\partial f}{\partial \rho _{\alpha _{1}\alpha _{2}\cdots \alpha _{i}}}}\ } ∇(i)⋅∂(∇(i)ρ)∂f=α1,α2,⋯,αi=1∑n ∂rα1∂rα2⋯∂rαi∂i ∂ρα1α2⋯αi∂f
比如,对于 n = 3 n=3 n=3, i = 2 i=2 i=2 的情况,张量标量积为:
∇ ( 2 ) ⋅ ∂ f ∂ ( ∇ ( 2 ) ρ ) = ∑ α , β = 1 3 ∂ 2 ∂ r α ∂ r β ∂ f ∂ ρ α β where ρ α β ≡ ∂ 2 ρ ∂ r α ∂ r β {\displaystyle \nabla ^{(2)}\cdot {\frac {\partial f}{\partial \left(\nabla ^{(2)}\rho \right)}}=\sum _{\alpha ,\beta =1}^{3}\ {\frac {\partial ^{\,2}}{\partial r_{\alpha }\,\partial r_{\beta }}}\ {\frac {\partial f}{\partial \rho _{\alpha \beta }}}\qquad {\text{where}}\ \ \rho _{\alpha \beta }\equiv {\frac {\partial ^{\,2}\rho }{\partial r_{\alpha }\,\partial r_{\beta }}}\ } ∇(2)⋅∂(∇(2)ρ)∂f=α,β=1∑3 ∂rα∂rβ∂2 ∂ραβ∂fwhere ραβ≡∂rα∂rβ∂2ρ
1927 年的 Thomas-Fermi model 在电子结构的密度泛函理论的第一次尝试中使用了非相互作用均匀电子气的动能泛函:
T T F [ ρ ] = C F ∫ ρ 5 / 3 ( r ) d r {\displaystyle T_{\mathrm {TF} }[\rho ]=C_{\mathrm {F} }\int \rho ^{5/3}(\mathbf {r} )\,\mathrm{d}\mathbf {r} \ } TTF[ρ]=CF∫ρ5/3(r)dr
由于 T T F [ ρ ] T_{\mathrm{TF}}[\rho] TTF[ρ] 的被积函数不涉及 ρ ( r ) \rho(\mathbf{r}) ρ(r) 的导数,因此 T T F [ ρ ] T_{\mathrm{TF}}[\rho] TTF[ρ] 的泛函导数为:
δ T T F δ ρ ( r ) = C F ∂ ρ 5 / 3 ( r ) ∂ ρ ( r ) = 5 3 C F ρ 2 / 3 ( r ) {\displaystyle {\begin{aligned}{\frac {\delta T_{\mathrm {TF} }}{\delta \rho ({\boldsymbol {r}})}}&=C_{\mathrm {F} } {\frac {\partial \rho ^{5/3}(\mathbf {r} )}{\partial \rho (\mathbf {r} )}}\\&={\frac {5}{3}} C_{\mathrm {F} }\rho ^{2/3}(\mathbf {r} )\,\end{aligned}}} δρ(r)δTTF=CF∂ρ(r)∂ρ5/3(r)=35CFρ2/3(r)
对于电子-核势(electron-nucleus potential),Thomas 和 Fermi 采用库仑势能泛函:
V [ ρ ] = ∫ ρ ( r ) ∣ r ∣ d r {\displaystyle V[\rho ]=\int {\frac {\rho ({\boldsymbol {r}})}{|{\boldsymbol {r}}|}}\ \mathrm{d}{\boldsymbol {r}}} V[ρ]=∫∣r∣ρ(r) dr
应用泛函导数的定义,
∫ δ V δ ρ ( r ) ϕ ( r ) d r = [ d d ε ∫ ρ ( r ) + ε ϕ ( r ) ∣ r ∣ d r ] ε = 0 = ∫ 1 ∣ r ∣ ϕ ( r ) d r {\displaystyle {\begin{aligned}\int {\frac {\delta V}{\delta \rho ({\boldsymbol {r}})}}\ \phi ({\boldsymbol {r}})\ \mathrm{d}{\boldsymbol {r}}&{}=\left[{\frac {\mathrm{d}}{\mathrm{d}\varepsilon }}\int {\frac {\rho ({\boldsymbol {r}})+\varepsilon \phi ({\boldsymbol {r}})}{|{\boldsymbol {r}}|}}\ \mathrm{d}{\boldsymbol {r}}\right]_{\varepsilon =0}\\&{}=\int {\frac {1}{|{\boldsymbol {r}}|}}\,\phi ({\boldsymbol {r}})\ \mathrm{d}{\boldsymbol {r}}\,\end{aligned}}} ∫δρ(r)δV ϕ(r) dr=[dεd∫∣r∣ρ(r)+εϕ(r) dr]ε=0=∫∣r∣1ϕ(r) dr
所以,
δ V δ ρ ( r ) = 1 ∣ r ∣ {\displaystyle {\frac {\delta V}{\delta \rho ({\boldsymbol {r}})}}={\frac {1}{|{\boldsymbol {r}}|}}\ } δρ(r)δV=∣r∣1
对于电子-电子相互作用的经典部分,Thomas 和 Fermi 采用了库仑势能泛函
J [ ρ ] = 1 2 ∬ ρ ( r ) ρ ( r ′ ) ∣ r − r ′ ∣ d r d r ′ {\displaystyle J[\rho ]={\frac {1}{2}}\iint {\frac {\rho (\mathbf {r} )\rho (\mathbf {r} ')}{|\mathbf { r} -\mathbf {r} '|}}\,\mathrm{d}\mathbf {r} \mathrm{d}\mathbf {r} '\,} J[ρ]=21∬∣r−r′∣ρ(r)ρ(r′)drdr′
从泛函导数的定义:
∫ δ J δ ρ ( r ) ϕ ( r ) d r = [ d d ϵ J [ ρ + ϵ ϕ ] ] ϵ = 0 = [ d d ϵ ( 1 2 ∬ [ ρ ( r ) + ϵ ϕ ( r ) ] [ ρ ( r ′ ) + ϵ ϕ ( r ′ ) ] ∣ r − r ′ ∣ d r d r ′ ) ] ϵ = 0 = 1 2 ∬ ρ ( r ′ ) ϕ ( r ) ∣ r − r ′ ∣ d r d r ′ + 1 2 ∬ ρ ( r ) ϕ ( r ′ ) ∣ r − r ′ ∣ d r d r ′ {\displaystyle {\begin{aligned}\int {\frac {\delta J}{\delta \rho ({\boldsymbol {r}})}}\phi ({\boldsymbol {r}})\mathrm{d}{\boldsymbol {r}}&{}=\left[{\frac {\mathrm{d}\ }{\mathrm{d}\epsilon }}\,J[\rho +\epsilon \phi ]\right]_{\epsilon =0}\\&{}=\left[{\frac {\mathrm{d}\ }{\mathrm{d}\epsilon }}\,\left({\frac {1}{2}}\iint {\frac {[\rho ({\boldsymbol {r}})+\epsilon \phi ({\boldsymbol {r}})]\,[\rho ({\boldsymbol {r}}')+\epsilon \phi ({\boldsymbol {r}}')]}{|{\boldsymbol {r}}-{\boldsymbol {r}}'|}}\,\mathrm{d}{\boldsymbol {r}}\mathrm{d}{\boldsymbol {r}}'\right)\right]_{\epsilon =0}\\&{}={\frac {1}{2}}\iint {\frac {\rho ({\boldsymbol {r}}')\phi ({\boldsymbol {r}})}{|{\boldsymbol {r}}-{\boldsymbol {r}}'|}}\,\mathrm{d}{\boldsymbol {r}}\mathrm{d}{\boldsymbol {r}}'+{\frac {1}{2}}\iint {\frac {\rho ({\boldsymbol {r}})\phi ({\boldsymbol {r}}')}{|{\boldsymbol {r}}-{\boldsymbol {r}}'|}}\,\mathrm{d}{\boldsymbol {r}}\mathrm{d}{\boldsymbol {r}}'\\\end{aligned}}} ∫δρ(r)δJϕ(r)dr=[dϵd J[ρ+ϵϕ]]ϵ=0=[dϵd (21∬∣r−r′∣[ρ(r)+ϵϕ(r)][ρ(r′)+ϵϕ(r′)]drdr′)]ϵ=0=21∬∣r−r′∣ρ(r′)ϕ(r)drdr′+21∬∣r−r′∣ρ(r)ϕ(r′)drdr′
最后一个方程右侧的第一项和第二项相等,因为第二项中的 r 和 r’ 可以互换,而无需改变积分的值。所以,
∫ δ J δ ρ ( r ) ϕ ( r ) d r = ∫ ( ∫ ρ ( r ′ ) ∣ r − r ′ ∣ d r ′ ) ϕ ( r ) d r {\displaystyle \int {\frac {\delta J}{\delta \rho ({\boldsymbol {r}})}}\phi ({\boldsymbol {r}})\mathrm{d}{\boldsymbol {r}}=\int \left(\int {\frac {\rho ({\boldsymbol {r}}')}{|{\boldsymbol {r}}-{\boldsymbol {r}}'|}}\mathrm{d}{\boldsymbol {r }}'\right)\phi ({\boldsymbol {r}})\mathrm{d}{\boldsymbol {r}}} ∫δρ(r)δJϕ(r)dr=∫(∫∣r−r′∣ρ(r′)dr′)ϕ(r)dr
电子-电子库仑势能泛函 J [ ρ ] J[\rho] J[ρ] 的泛函导数为:
δ J δ ρ ( r ) = ∫ ρ ( r ′ ) ∣ r − r ′ ∣ d r ′ {\displaystyle {\frac {\delta J}{\delta \rho ({\boldsymbol {r}})}}=\int {\frac {\rho ({\boldsymbol {r}}')}{|{ \boldsymbol {r}}-{\boldsymbol {r}}'|}}d{\boldsymbol {r}}'\,} δρ(r)δJ=∫∣r−r′∣ρ(r′)dr′
二阶泛函导数是:
δ 2 J [ ρ ] δ ρ ( r ′ ) δ ρ ( r ) = ∂ ∂ ρ ( r ′ ) ( ρ ( r ′ ) ∣ r − r ′ ∣ ) = 1 ∣ r − r ′ ∣ {\displaystyle {\frac {\delta^{2}J[\rho]}{\delta\rho(\mathbf{r}')\delta\rho(\mathbf{r})}}={\frac { \partial }{\partial \rho(\mathbf{r}')}}\left({\frac{\rho(\mathbf{r}')}{|\mathbf{r} -\mathbf{r}' |}}\right)={\frac{1}{|\mathbf{r} -\mathbf{r}'|}}} δρ(r′)δρ(r)δ2J[ρ]=∂ρ(r′)∂(∣r−r′∣ρ(r′))=∣r−r′∣1
1935 年 von Weizsäcker 提议对 Thomas-Fermi 动能泛函添加梯度校正,以使其更适合分子电子云:
T W [ ρ ] = 1 8 ∫ ∇ ρ ( r ) ⋅ ∇ ρ ( r ) ρ ( r ) d r = ∫ t W d r {\displaystyle T_{\mathrm {W} }[\rho ]={\frac {1}{8}}\int {\frac {\nabla \rho (\mathbf {r} )\cdot \nabla \rho (\mathbf {r} )}{\rho (\mathbf {r} )}}d\mathbf {r} =\int t_{\mathrm {W} }\ d\mathbf {r} \,} TW[ρ]=81∫ρ(r)∇ρ(r)⋅∇ρ(r)dr=∫tW dr
其中
t W ≡ 1 8 ∇ ρ ⋅ ∇ ρ ρ and ρ = ρ ( r ) {\displaystyle t_{\mathrm {W} }\equiv {\frac {1}{8}}{\frac {\nabla \rho \cdot \nabla \rho }{\rho }}\quad {\text{and}}\ \ \rho =\rho ({\boldsymbol {r}})\ } tW≡81ρ∇ρ⋅∇ρand ρ=ρ(r)
使用先前导出的泛函导数公式:
δ T W δ ρ ( r ) = ∂ t W ∂ ρ − ∇ ⋅ ∂ t W ∂ ∇ ρ = − 1 8 ∇ ρ ⋅ ∇ ρ ρ 2 − ( 1 4 ∇ 2 ρ ρ − 1 4 ∇ ρ ⋅ ∇ ρ ρ 2 ) where ∇ 2 = ∇ ⋅ ∇ , {\displaystyle {\begin{aligned}{\frac {\delta T_{\mathrm {W} }}{\delta \rho ({\boldsymbol {r}})}}&={\frac {\partial t_{\mathrm {W} }}{\partial \rho }}-\nabla \cdot {\frac {\partial t_{\mathrm {W} }}{\partial \nabla \rho }}\\&=-{\frac {1}{8}}{\frac {\nabla \rho \cdot \nabla \rho }{\rho ^{2}}}-\left({\frac {1}{4}}{\frac {\nabla ^{2}\rho }{\rho }}-{\frac {1}{4}}{\frac {\nabla \rho \cdot \nabla \rho }{\rho ^{2}}}\right)\qquad {\text{where}}\ \ \nabla ^{2}=\nabla \cdot \nabla \ ,\end{aligned}}} δρ(r)δTW=∂ρ∂tW−∇⋅∂∇ρ∂tW=−81ρ2∇ρ⋅∇ρ−(41ρ∇2ρ−41ρ2∇ρ⋅∇ρ)where ∇2=∇⋅∇ ,
结果是:
δ T W δ ρ ( r ) = 1 8 ∇ ρ ⋅ ∇ ρ ρ 2 − 1 4 ∇ 2 ρ ρ {\displaystyle {\frac {\delta T_{\mathrm {W} }}{\delta \rho ({\boldsymbol {r}})}}=\ \ \,{\frac {1}{8}}{\frac {\nabla \rho \cdot \nabla \rho }{\rho ^{2}}}-{\frac {1}{4}}{\frac {\nabla ^{2}\rho }{\rho }}\ } δρ(r)δTW= 81ρ2∇ρ⋅∇ρ−41ρ∇2ρ
离散随机变量的熵是概率质量函数(probability mass function)的泛函。
H [ p ( x ) ] = − ∑ x p ( x ) log p ( x ) {\displaystyle H[p(x)]=-\sum _{x}p(x)\log p(x)} H[p(x)]=−x∑p(x)logp(x)
因此,
∑ x δ H δ p ( x ) ϕ ( x ) = [ d d ϵ H [ p ( x ) + ϵ ϕ ( x ) ] ] ϵ = 0 = [ − d d ε ∑ x [ p ( x ) + ε ϕ ( x ) ] log [ p ( x ) + ε ϕ ( x ) ] ] ε = 0 = − ∑ x [ 1 + log p ( x ) ] ϕ ( x ) {\displaystyle {\begin{aligned}\sum _{x}{\frac {\delta H}{\delta p(x)}}\,\phi (x)&{}=\left[{\frac {\mathrm{d}}{\mathrm{d}\epsilon }}H[p(x)+\epsilon \phi (x)]\right]_{\epsilon =0}\\&{}=\left[-\,{\frac {\mathrm{d}}{\mathrm{d}\varepsilon }}\sum _{x}\,[p(x)+\varepsilon \phi (x)]\ \log[p(x)+\varepsilon \phi (x)]\right]_{\varepsilon =0}\\&{}=-\sum _{x}\,[1+\log p(x)]\ \phi (x)\,\end{aligned}}} x∑δp(x)δHϕ(x)=[dϵdH[p(x)+ϵϕ(x)]]ϵ=0=[−dεdx∑[p(x)+εϕ(x)] log[p(x)+εϕ(x)]]ε=0=−x∑[1+logp(x)] ϕ(x)
因此,
δ H δ p ( x ) = − 1 − log p ( x ) {\displaystyle {\frac {\delta H}{\delta p(x)}}=-1-\log p(x)} δp(x)δH=−1−logp(x)
让
F [ φ ( x ) ] = e ∫ φ ( x ) g ( x ) d x {\displaystyle F[\varphi (x)]=e^{\int \varphi (x)g(x)dx}} F[φ(x)]=e∫φ(x)g(x)dx
使用 delta 函数作为测试函数:
δ F [ φ ( x ) ] δ φ ( y ) = lim ε → 0 F [ φ ( x ) + ε δ ( x − y ) ] − F [ φ ( x ) ] ε = lim ε → 0 e ∫ ( φ ( x ) + ε δ ( x − y ) ) g ( x ) d x − e ∫ φ ( x ) g ( x ) d x ε = e ∫ φ ( x ) g ( x ) d x lim ε → 0 e ε ∫ δ ( x − y ) g ( x ) d x − 1 ε = e ∫ φ ( x ) g ( x ) d x lim ε → 0 e ε g ( y ) − 1 ε = e ∫ φ ( x ) g ( x ) d x g ( y ) {\displaystyle {\begin{aligned}{\frac {\delta F[\varphi (x)]}{\delta \varphi (y)}}&{}=\lim _{\varepsilon \to 0}{\frac {F[\varphi (x)+\varepsilon \delta (x-y)]-F[\varphi (x)]}{\varepsilon }}\\&{}=\lim _{\varepsilon \to 0}{\frac {e^{\int (\varphi (x)+\varepsilon \delta (x-y))g(x)dx}-e^{\int \varphi (x)g(x)dx}}{\varepsilon }}\\&{}=e^{\int \varphi (x)g(x)dx}\lim _{\varepsilon \to 0}{\frac {e^{\varepsilon \int \delta (x-y)g(x)dx}-1}{\varepsilon }}\\&{}=e^{\int \varphi (x)g(x)dx}\lim _{\varepsilon \to 0}{\frac {e^{\varepsilon g(y)}-1}{\varepsilon }}\\&{}=e^{\int \varphi (x)g(x)dx}g(y)\end{aligned}}} δφ(y)δF[φ(x)]=ε→0limεF[φ(x)+εδ(x−y)]−F[φ(x)]=ε→0limεe∫(φ(x)+εδ(x−y))g(x)dx−e∫φ(x)g(x)dx=e∫φ(x)g(x)dxε→0limεeε∫δ(x−y)g(x)dx−1=e∫φ(x)g(x)dxε→0limεeεg(y)−1=e∫φ(x)g(x)dxg(y)
因而:
δ F [ φ ( x ) ] δ φ ( y ) = g ( y ) F [ φ ( x ) ] {\displaystyle {\frac {\delta F[\varphi (x)]}{\delta \varphi (y)}}=g(y)F[\varphi (x)]} δφ(y)δF[φ(x)]=g(y)F[φ(x)]
这对于使用量子场论中的配分函数,来计算相关函数(correlation functions)特别有用。
函数可以像泛函一样写成积分的形式。例如,
ρ ( r ) = F [ ρ ] = ∫ ρ ( r ′ ) δ ( r − r ′ ) d r ′ {\displaystyle \rho ({\boldsymbol {r}})=F[\rho ]=\int \rho ({\boldsymbol {r}}')\delta ({\boldsymbol {r}}-{\boldsymbol { r}}')\,\mathrm{d}{\boldsymbol {r}}'} ρ(r)=F[ρ]=∫ρ(r′)δ(r−r′)dr′
由于被积函数不依赖于 ρ \rho ρ 的导数,因此 ρ ( r ) \rho(\boldsymbol{r}) ρ(r) 的泛函导数是:
δ ρ ( r ) δ ρ ( r ′ ) ≡ δ F δ ρ ( r ′ ) = ∂ ∂ ρ ( r ′ ) [ ρ ( r ′ ) δ ( r − r ′ ) ] = δ ( r − r ′ ) {\displaystyle {\begin{aligned}{\frac {\delta \rho ({\boldsymbol {r}})}{\delta \rho ({\boldsymbol {r}}')}}\equiv {\frac { \delta F}{\delta \rho ({\boldsymbol {r}}')}}&={\frac {\partial \ \ }{\partial \rho ({\boldsymbol {r}}')}}\,[\rho ({\boldsymbol {r}}')\delta ({\boldsymbol {r}}-{\boldsymbol {r}}')]\\&=\delta ({\boldsymbol {r}}- {\boldsymbol {r}}')\end{aligned}}} δρ(r′)δρ(r)≡δρ(r′)δF=∂ρ(r′)∂ [ρ(r′)δ(r−r′)]=δ(r−r′)
迭代函数 f ( f ( x ) ) f(f(x)) f(f(x)) 的泛函导数由下式给出:
δ f ( f ( x ) ) δ f ( y ) = f ′ ( f ( x ) ) δ ( x − y ) + δ ( f ( x ) − y ) {\displaystyle {\frac {\delta f(f(x))}{\delta f(y)}}=f'(f(x))\delta (x-y)+\delta (f(x)-y )} δf(y)δf(f(x))=f′(f(x))δ(x−y)+δ(f(x)−y)
和
δ f ( f ( f ( x ) ) ) δ f ( y ) = f ′ ( f ( f ( x ) ) ( f ′ ( f ( x ) ) δ ( x − y ) + δ ( f ( x ) − y ) ) + δ ( f ( f ( x ) ) − y ) {\displaystyle {\frac {\delta f(f(f(x)))}{\delta f(y)}}=f'(f(f(x))(f'(f(x))\delta (x-y)+\delta (f(x)-y))+\delta (f(f(x))-y)} δf(y)δf(f(f(x)))=f′(f(f(x))(f′(f(x))δ(x−y)+δ(f(x)−y))+δ(f(f(x))−y)
一般来说:
δ f N ( x ) δ f ( y ) = f ′ ( f N − 1 ( x ) ) δ f N − 1 ( x ) δ f ( y ) + δ ( f N − 1 ( x ) − y ) {\displaystyle {\frac {\delta f^{N}(x)}{\delta f(y)}}=f'(f^{N-1}(x)){\frac {\delta f^ {N-1}(x)}{\delta f(y)}}+\delta (f^{N-1}(x)-y)} δf(y)δfN(x)=f′(fN−1(x))δf(y)δfN−1(x)+δ(fN−1(x)−y)
放入 N = 0 N = 0 N=0 给出:
δ f − 1 ( x ) δ f ( y ) = − δ ( f − 1 ( x ) − y ) f ′ ( f − 1 ( x ) ) {\displaystyle {\frac {\delta f^{-1}(x)}{\delta f(y)}}=-{\frac {\delta (f^{-1}(x)-y)} {f'(f^{-1}(x))}}} δf(y)δf−1(x)=−f′(f−1(x))δ(f−1(x)−y)
在物理学中,通常使用狄拉克 delta 函数 δ ( x − y ) \delta (x-y) δ(x−y) 代替通用测试函数 ϕ ( x ) \phi (x) ϕ(x),以得到 y y y 点的泛函导数(这是整个泛函导数的一个点,因为偏导数是梯度的一个分量):
δ F [ ρ ( x ) ] δ ρ ( y ) = lim ε → 0 F [ ρ ( x ) + ε δ ( x − y ) ] − F [ ρ ( x ) ] ε {\displaystyle {\frac {\delta F[\rho (x)]}{\delta \rho (y)}}=\lim _{\varepsilon \to 0}{\frac {F[\rho (x) +\varepsilon \delta (x-y)]-F[\rho (x)]}{\varepsilon }}} δρ(y)δF[ρ(x)]=ε→0limεF[ρ(x)+εδ(x−y)]−F[ρ(x)]
这适用于 F [ ρ ( x ) + ε f ( x ) ] F[\rho (x)+\varepsilon f(x)] F[ρ(x)+εf(x)] 形式上可以扩展为一个级数的情况(或至少 ε \varepsilon ε 中的第一阶)。然而,该公式在数学上并不严格,因为 F [ ρ ( x ) + ε δ ( x − y ) ] F[\rho (x)+\varepsilon \delta (x-y)] F[ρ(x)+εδ(x−y)] 通常甚至没有定义。
上一节给出的定义是基于对所有测试函数 ϕ ( x ) \phi (x) ϕ(x) 都成立的关系,所以人们可能认为它也应该成立,当 ϕ ( x ) \phi (x) ϕ(x) 被选为特定函数,例如 delta 函数。然而,后者不是一个有效的测试函数(它甚至不是一个正确的函数)。
在定义中,泛函导数描述了泛函 F [ ρ ( x ) ] F[\rho (x)] F[ρ(x)] 如何随着整个函数 ρ ( x ) \rho (x) ρ(x) 的微小变化而变化。 ρ ( x ) \rho (x) ρ(x) 的具体变化形式没有指定,但它应该延伸到定义 x x x 的整个区间。使用由 delta 函数给出的特定形式的扰动意味着 ρ ( x ) \rho (x) ρ(x) 仅在点 y y y 处变化。除了这一点, ρ ( x ) \rho (x) ρ(x) 没有变化。
在变分法和经典力学中,欧拉-拉格朗日方程是一个二阶常微分方程组,其解是给定作用泛函的驻点。这些方程是在 1750 年代由瑞士数学家 Leonhard Euler 和意大利数学家 Joseph-Louis Lagrange 发现的。
因为可微泛函在其局部极值处是静止的,所以欧拉-拉格朗日方程可用于解决优化问题,在这些问题中,给定一些泛函,人们寻求函数使其最小化或最大化。这类似于微积分中的费马定理,指出在可微函数达到局部极值的任何点,其导数为零。在拉格朗日力学中,根据汉密尔顿的静止作用原理,物理系统的演化是由系统作用的欧拉方程的解来描述的。在这种情况下,欧拉方程通常称为拉格朗日方程。在经典力学中,它等价于牛顿运动定律;事实上,欧拉-拉格朗日方程将产生与牛顿定律相同的方程。这在分析力矢量特别复杂的系统时特别有用。它的优点是在任何广义坐标系中都采用相同的形式,并且更适合泛化。在经典场论中,有一个类似的方程来计算场的动力学。
Euler-Lagrange 方程是在 1750 年代由 Euler 和 Lagrange 在他们对 tautochrone 问题的研究中开发的。这是确定一条曲线的问题,在该曲线上,加权粒子将在固定的时间内落到固定点,与起点无关。
拉格朗日在 1755 年解决了这个问题,并将解决方案发送给欧拉。两者都进一步发展了拉格朗日方法并将其应用于力学,从而形成了拉格朗日力学。他们的通信最终导致了变分法,这是欧拉本人在 1766 年创造的一个术语。
令 ( X , L ) (X,L) (X,L) 是一个具有 n n n 自由度的机械系统。这里 X X X 是配置空间, L = L ( t , q , v ) L=L(t,{\boldsymbol {q}},{\boldsymbol {v}}) L=L(t,q,v) 拉格朗日函数,即平滑实值函数,使得 q ∈ X {\boldsymbol {q}}\in X q∈X 和 v {\boldsymbol {v}} v 是一个 n n n 维“速度向量”。(对于那些熟悉微分几何的人来说, X X X 是一个光滑流形,而 L : R t × T X → R L:{\mathbb {R} }_{t}\times TX\to {\mathbb {R} } L:Rt×TX→R 其中 T X TX TX 是 X X X 的切丛(tangent bundle))。
让 P ( a , b , x a , x b ) \mathcal{P}(a,b,{\boldsymbol {x}}_{a},{\boldsymbol {x}}_{b}) P(a,b,xa,xb) 是平滑路径的集合 q : [ a , b ] → X {\boldsymbol {q}}:[a ,b]\to X q:[a,b]→X 其中 q ( a ) = x a {\boldsymbol {q}}(a)={\boldsymbol {x}} _{a} q(a)=xa 和 q ( b ) = x b {\boldsymbol {q}}(b)={\boldsymbol {x}}_ {b} q(b)=xb 动作泛函 S : P ( a , b , x a , x b ) → R S:{\cal {P}}(a, b,{\boldsymbol {x}}_{a},{\boldsymbol {x}}_{b})\to \mathbb {R} S:P(a,b,xa,xb)→R 定义为
S [ q ] = ∫ a b L ( t , q ( t ) , q ˙ ( t ) ) d t S[{\boldsymbol {q}}]=\int _{a}^{b}L(t,{\boldsymbol {q}}(t),{\dot {\boldsymbol {q}}} (t))\,dt S[q]=∫abL(t,q(t),q˙(t))dt
一条路径 q ∈ P ( a , b , x a , x b ) {\boldsymbol {q}}\in {\cal {P}}(a,b,{\boldsymbol {x}}_{a},{\boldsymbol {x}}_{b}) q∈P(a,b,xa,xb) 是 S S S 的驻点(stationary point),当且仅当
∂ L ∂ q i ( t , q ( t ) , q ˙ ( t ) ) − d d t ∂ L ∂ q ˙ i ( t , q ( t ) , q ˙ ( t ) ) = 0 , i = 1 , … , n {\frac {\partial L}{\partial q^{i}}}(t,{\boldsymbol {q}}(t),{\dot {\boldsymbol {q}}}(t)) -{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {q}}^{i}}}(t,{\boldsymbol {q}}(t),{\dot {\boldsymbol {q}}}(t))=0,\quad i=1,\dots ,n ∂qi∂L(t,q(t),q˙(t))−dtd∂q˙i∂L(t,q(t),q˙(t))=0,i=1,…,n
这里, q ˙ ( t ) {\dot {\boldsymbol {q}}}(t) q˙(t) 是 q ( t ) {\boldsymbol {q}}(t) q(t) 对时间的导数。
求泛函的极值类似于求函数的最大值和最小值。函数的最大值和最小值可以通过找到其导数等于零的点来定位。泛函的极值可以通过寻找泛函导数为零的函数来获得。这导致了求解相关的欧拉-拉格朗日方程的引入。
考虑泛函:
J [ y ] = ∫ x 1 x 2 L ( x , y ( x ) , y ′ ( x ) ) d x J[y]=\int _{x_{1}}^{x_{2}}L\left(x,y(x),y'(x)\right)\,\mathrm{d}x J[y]=∫x1x2L(x,y(x),y′(x))dx
其中
x
1
x_{1}
x1,
x
2
x_{2}
x2 是常数,
y
(
x
)
y(x)
y(x) 是两次连续可微的,
y
′
(
x
)
=
d
y
d
x
y'(x)={\frac {dy}{dx}}
y′(x)=dxdy,
L
(
x
,
y
(
x
)
,
y
′
(
x
)
)
L\left(x,y(x),y'(x)\right)
L(x,y(x),y′(x))关于它的参数
x
x
x,
y
y
y,
y
′
y'
y′两次连续可微。(可以使用一个较弱的假设,但证明变得更加困难。)
如果泛函 J [ y ] J[y] J[y] 在 f f f 处达到局部最小值(当然也可以讨论极大值,而与下述推导一致),并且 η ( x ) \eta (x) η(x) 是任意具有至少一个导数并且在端点 x 1 x_{1} x1 和 x 2 x_{2} x2 处消失( η ( x 1 ) = 0 = η ( x 2 ) \eta(x_{1})=0=\eta(x_{2}) η(x1)=0=η(x2))的函数,那么对于任意数 ε → 0 \varepsilon\rightarrow 0 ε→0:
J [ f ] ≤ J [ f + ε η ] J[f]\leq J[f+\varepsilon \eta] J[f]≤J[f+εη]
ε η \varepsilon \eta εη 称为函数 f f f 的变分,记为 δ f \delta f δf。
在泛函 J [ y ] J[y] J[y] 中将 y y y 替换为 f + ε η f+\varepsilon \eta f+εη,结果为 ε \varepsilon ε 的函数:
Φ ( ε ) = J [ f + ε η ] \Phi (\varepsilon )=J[f+\varepsilon \eta ] Φ(ε)=J[f+εη]
由于泛函 J [ y ] J[y] J[y] 对 y = f y=f y=f 有最小值,所以函数 Φ ( ε ) \Phi (\varepsilon) Φ(ε) 在 ε = 0 \varepsilon =0 ε=0 处有最小值,因此:
Φ ′ ( 0 ) ≡ d Φ d ε ∣ ε = 0 = ∫ x 1 x 2 d L d ε ∣ ε = 0 d x = 0 \Phi '(0)\equiv \left.{\frac {\mathrm{d}\Phi }{\mathrm{d}\varepsilon }}\right|_{\varepsilon =0}=\int _{x_{1}}^{ x_{2}}\left.{\frac {\mathrm{d}L}{\mathrm{d}\varepsilon }}\right|_{\varepsilon =0}\mathrm{d}x=0 Φ′(0)≡dεdΦ ε=0=∫x1x2dεdL ε=0dx=0
取 L [ x , y , y ′ ] L\left[x,y,y'\right] L[x,y,y′] 的全导数(total derivative),其中 y = f + ε η y=f+\varepsilon\eta y=f+εη 和 y ′ = f ′ + ε η ′ y'=f'+\varepsilon \eta ' y′=f′+εη′ 被认为是 ε \varepsilon ε 而不是 x x x 的函数,产生
d L d ε = ∂ L ∂ x d x d ε + ∂ L ∂ y d y d ε + ∂ L ∂ y ′ d y ′ d ε = ∂ L ∂ y d y d ε + ∂ L ∂ y ′ d y ′ d ε \begin{aligned} \frac {\mathrm{d}L}{\mathrm{d}\varepsilon } &=\frac {\partial L}{\partial x}\frac {\mathrm{d}x}{\mathrm{d}\varepsilon }+\frac {\partial L}{\partial y}\frac {\mathrm{d}y}{\mathrm{d}\varepsilon }+\frac {\partial L }{\partial y'}\frac {\mathrm{d}y'}{\mathrm{d}\varepsilon}\\ &=\frac {\partial L}{\partial y}\frac {\mathrm{d}y}{\mathrm{d}\varepsilon }+\frac {\partial L }{\partial y'}\frac {\mathrm{d}y'}{\mathrm{d}\varepsilon} \end{aligned} dεdL=∂x∂Ldεdx+∂y∂Ldεdy+∂y′∂Ldεdy′=∂y∂Ldεdy+∂y′∂Ldεdy′
其中由于变量 x x x 与 ε \varepsilon ε 不相关,所以 d x d ε = 0 ⇒ ∂ L ∂ x d x d ε = 0 \frac {\mathrm{d}x}{\mathrm{d}\varepsilon }=0\Rightarrow \frac {\partial L}{\partial x}\frac {\mathrm{d}x}{\mathrm{d}\varepsilon }=0 dεdx=0⇒∂x∂Ldεdx=0。
因为 d y d ε = η \frac {\mathrm{d}y}{\mathrm{d}\varepsilon }=\eta dεdy=η 和 d y ′ d ε = η ′ \frac {\mathrm{d}y' }{\mathrm{d}\varepsilon }=\eta ' dεdy′=η′:
d L d ε = ∂ L ∂ y η + ∂ L ∂ y ′ η ′ \frac {\mathrm{d}L}{\mathrm{d}\varepsilon}=\frac {\partial L}{\partial y}\eta +\frac {\partial L}{\partial y'}\eta ' dεdL=∂y∂Lη+∂y′∂Lη′
所以 ϵ = 0 \epsilon=0 ϵ=0 时,上式中的 y = f y=f y=f,于是上式变为:
d L d ε = ∂ L ∂ f η + ∂ L ∂ f ′ η ′ \frac {\mathrm{d}L}{\mathrm{d}\varepsilon}=\frac {\partial L}{\partial f}\eta +\frac {\partial L}{\partial f'}\eta ' dεdL=∂f∂Lη+∂f′∂Lη′
所以:
∫ x 1 x 2 d L d ε ∣ ε = 0 d x = ∫ x 1 x 2 ( ∂ L ∂ f η + ∂ L ∂ f ′ η ′ ) d x = ∫ x 1 x 2 ∂ L ∂ f η d x + ∂ L ∂ f ′ η ∣ x 1 x 2 − ∫ x 1 x 2 η d d x ∂ L ∂ f ′ d x = ∫ x 1 x 2 ( ∂ L ∂ f η − η d d x ∂ L ∂ f ′ ) d x \begin{aligned} \int _{x_{1}}^{x_{2}}\left.{\frac {\mathrm{d}L}{\mathrm{d}\varepsilon }}\right|_{\varepsilon =0} \mathrm{d}x &=\int _{x_{1}}^{x_{2}}\left({\frac {\partial L}{\partial f}}\eta +{\frac {\partial L}{\partial f '}}\eta '\right)\,\mathrm{d}x\\ &=\int _{x_{1}}^{x_{2}}{\frac {\partial L}{\partial f}}\eta \, \mathrm{d}x+\left.{\frac {\partial L}{\partial f'}}\eta \right|_{x_{1}}^{x_{2}}-\int _{x_{1}}^{ x_{2}}\eta {\frac {\mathrm{d}}{\mathrm{d}x}}{\frac {\partial L}{\partial f'}}\,\mathrm{d}x\\ &=\int _{x_{1}}^{ x_{2}}\left({\frac {\partial L}{\partial f}}\eta -\eta {\frac {\mathrm{d}}{\mathrm{d}x}}{\frac {\partial L}{\partial f' }}\right)\,\mathrm{d}x\\ \end{aligned} ∫x1x2dεdL ε=0dx=∫x1x2(∂f∂Lη+∂f′∂Lη′)dx=∫x1x2∂f∂Lηdx+∂f′∂Lη x1x2−∫x1x2ηdxd∂f′∂Ldx=∫x1x2(∂f∂Lη−ηdxd∂f′∂L)dx
其中当 ε = 0 \varepsilon =0 ε=0, L [ x , y , y ′ ] → L [ x , f , f ′ ] L\left[x,y,y'\right]\to L\left[x,f,f'\right] L[x,y,y′]→L[x,f,f′] ,推导中在第二项中使用了部分积分。第二行的第二项消失了,因为根据定义, η ( x 1 ) = 0 = η ( x 2 ) \eta(x_{1})=0=\eta(x_{2}) η(x1)=0=η(x2)。此外,如前所述,等式的左侧为零,因此:
∫ x 1 x 2 η ( x ) ( ∂ L ∂ f − d d x ∂ L ∂ f ′ ) d x = 0 \int _{x_{1}}^{x_{2}}\eta (x)\left({\frac {\partial L}{\partial f}}-{\frac {\mathrm{d}}{\mathrm{d}x }}{\frac {\partial L}{\partial f'}}\right)\,\mathrm{d}x=0 ∫x1x2η(x)(∂f∂L−dxd∂f′∂L)dx=0
根据变分法的基本引理(fundamental lemma of calculus of variations),括号中被积函数的部分为零,即
∂ L ∂ f − d d x ∂ L ∂ f ′ = 0 {\frac {\partial L}{\partial f}}-{\frac {\mathrm{d}}{\mathrm{d}x}}{\frac {\partial L}{\partial f'}}=0 ∂f∂L−dxd∂f′∂L=0
这称为欧拉-拉格朗日方程(Euler-Lagrange equation)。这个方程的左边称为 J [ f ] J[f] J[f] 的泛函导数,记为 δ J / δ f ( x ) \delta J/\delta f(x) δJ/δf(x)。
一般来说,这给出了一个二阶常微分方程,可以求解该方程以获得极值函数 f ( x ) f(x) f(x)。欧拉-拉格朗日方程是极值 J [ f ] J[f] J[f] 极值的必要条件,但不是充分条件。最小值的充分条件在后面变分和充分条件相关部分给出。
给定一个泛函
J = ∫ a b L ( t , y ( t ) , y ′ ( t ) ) d t J=\int _{a}^{b}L(t,y(t),y'(t))\,\mathrm {d} t J=∫abL(t,y(t),y′(t))dt
在 C 1 ( [ a , b ] ) C^{1}([a,b]) C1([a,b]) 上,边界条件为 y ( a ) = A y(a)=A y(a)=A 和 y ( b ) = B y(b)=B y(b)=B,我们通过一条具有 n n n 段的折线来逼近极值曲线,并随着段数任意增长而达到极限。
将区间 [ a , b ] [a,b] [a,b] 分成 n n n 等段,端点为 t 0 = a , t 1 , t 2 , … , t n = b t_{0}=a,t_{1},t_{2},\ldots ,t_{n}=b t0=a,t1,t2,…,tn=b 并令 Δ t = t k − t k − 1 \Delta t=t_{k}-t_{ k-1} Δt=tk−tk−1。我们不考虑平滑函数 y ( t ) y(t) y(t),而是考虑具有顶点 ( t 0 , y 0 ) , … , ( t n , y n ) (t_{0},y_{0}),\ldots ,(t_{n},y_{ n}) (t0,y0),…,(tn,yn),其中 y 0 = A y_{0}=A y0=A 和 y n = B y_{n}=B yn=B。因此,我们的泛函变成了 n − 1 n-1 n−1 个变量的实函数,由下式给出
J ( y 1 , … , y n − 1 ) ≈ ∑ k = 0 n − 1 L ( t k , y k , y k + 1 − y k Δ t ) Δ t J(y_{1},\ldots ,y_{n-1})\approx \sum _{k=0}^{n-1}L\left(t_{k},y_{k}, {\frac {y_{k+1}-y_{k}}{\Delta t}}\right)\Delta t J(y1,…,yn−1)≈k=0∑n−1L(tk,yk,Δtyk+1−yk)Δt
在离散点 t 0 , … , t n t_{0},\ldots ,t_{n} t0,…,tn 上定义的这个新函数的极值对应于
∂ J ( y 1 , … , y n ) ∂ y m = 0 \frac {\partial J(y_{1},\ldots ,y_{n})}{\partial y_{m}}=0 ∂ym∂J(y1,…,yn)=0
求偏导可得:
∂ J ∂ y m = L y ( t m , y m , y m + 1 − y m Δ t ) Δ t + L y ′ ( t m − 1 , y m − 1 , y m − y m − 1 Δ t ) − L y ′ ( t m , y m , y m + 1 − y m Δ t ) {\frac {\partial J}{\partial y_{m}}}=L_{y}\left(t_{m},y_{m},{\frac {y_{m+1}-y_ {m}}{\Delta t}}\right)\Delta t+L_{y'}\left(t_{m-1},y_{m-1},{\frac {y_{m}-y_{ m-1}}{\Delta t}}\right)-L_{y'}\left(t_{m},y_{m},{\frac {y_{m+1}-y_{m}}{ \Delta t}}\right) ∂ym∂J=Ly(tm,ym,Δtym+1−ym)Δt+Ly′(tm−1,ym−1,Δtym−ym−1)−Ly′(tm,ym,Δtym+1−ym)
将上述方程除以 Δ t \Delta t Δt 得到:
∂ J ∂ y m Δ t = L y ( t m , y m , y m + 1 − y m Δ t ) − 1 Δ t [ L y ′ ( t m , y m , y m + 1 − y m Δ t ) − L y ′ ( t m − 1 , y m − 1 , f r a c y m − y m − 1 Δ t ) ] {\frac {\partial J}{\partial y_{m}\Delta t}}=L_{y}\left(t_{m},y_{m},{\frac {y_{m+1 }-y_{m}}{\Delta t}}\right)-{\frac {1}{\Delta t}}\left[L_{y'}\left(t_{m},y_{m}, {\frac {y_{m+1}-y_{m}}{\Delta t}}\right)-L_{y'}\left(t_{m-1},y_{m-1},{\ frac {y_{m}-y_{m-1}}{\Delta t}}\right)\right] ∂ymΔt∂J=Ly(tm,ym,Δtym+1−ym)−Δt1[Ly′(tm,ym,Δtym+1−ym)−Ly′(tm−1,ym−1, fracym−ym−1Δt)]
并将该表达式右侧的极限设为 Δ t → 0 \Delta t\to 0 Δt→0 得到:
L y − d d t L y ′ = 0 L_{y}-{\frac {\mathrm {d} }{\mathrm {d} t}}L_{y'}=0 Ly−dtdLy′=0
上式的左边是泛函 J J J 的泛函导数 δ J / δ y \delta J/\delta y δJ/δy。可微泛函在某个函数上具有极值的必要条件是它在该函数处的泛函导数消失,这是由最后一个方程所认可的。
