1. 奇异值分解(SVD)
(1)奇异值分解
已知矩阵\(\bm{A} \in \R^{m \times n}\), 其奇异值分解为:
\[\bm{A} = \bm{U}\bm{S}\bm{V}^T \]
其中\(\bm{U} \in \R^{m \times m}\),\(\bm{V} \in \R^{n \times n}\)是正交矩阵,\(\bm{S} \in \R^{m \times n}\)是对角线矩阵。\(\bm{S}\)的对角线元素\(\bm{s}_1, \bm{s}_2,..., \bm{s}_{\min(m,n)}\)是矩阵的奇异值。
(2) 奇异值分解的求解
而求矩阵的奇异值的算法非常简单,对于实数域下的矩阵\(A\),我们只需要求\(A^TA\)的特征值和特征向量。其特征向量归一化后即右奇异向量\(\bm{v}_1,\bm{v}_2,...,\bm{v}_n\),其特征值开根号即对应的奇异值\(\bm{s}_1, \bm{s}_2,..., \bm{s}_{\min(m,n)}\)。 然后由等式
\[\bm{A}\bm{v}_1=s_1\bm{u}_1, \\ \bm{A}\bm{v}_2=s_2\bm{u}_2, \\ ..., \\ A\bm{v}_{\min(m,n)} = \bm{s}_{\min(m,n)}\bm{u}_{\min(m,n)}\]
依次计算出相应的\(\bm{u}_i\)向量的值。
至于特征值的计算,采用 QR 算法,此处不予介绍,这里可以直接调用 np.linalg.eig()函数实现。以下给出奇异值计算代码实例(此处仅为知识演示,具体的工业级别的奇异值计算算法要复杂得多,参考 Golub 与 Van Loan《矩阵计算》)
import numpy as np
def svd(A):
eigen_values, eigen_vectors = np.linalg.eig(A.T.dot(A))
singular_values = np.sqrt(eigen_values)
#这里奇异值要从大到小排序,特征向量也要随之从大到小排
val_vec = [] #存储奇异值-特征向量对
for i in range(len(eigen_values)):
val_vec.append((singular_values[i], eigen_vectors[:, i]))
val_vec.sort(key = lambda x:-x[0])
singular_values = [ pair[0] for pair in val_vec]
eigen_vectors = [ pair[1] for pair in val_vec]
# 在计算左奇异向量之前,先要对右奇异向量也就是特征向量组成的基正交化
# 不过linalg.eig返回的是已经正交化的,这一步可省略
# 由等式Avi = siui(vi是右奇异向量, ui是左奇异向量)
# 依次计算左奇异向量
U = np.zeros((A.shape[0], A.shape[1]))
for i in range(A.shape[1]):
u = A.dot(eigen_vectors[i])/singular_values[i]
U[:, i] = u
# 给U加上标准正交基去构造R3的基
for i in range(A.shape[1], A.shape[0]):
basis = np.zeros((A.shape[0], 1))
basis[i] = 1
U = np.concatenate([U, basis], axis=1)
eigen_vectors = [vec.reshape(-1, 1) for vec in eigen_vectors]
eigen_vectors = np.concatenate(eigen_vectors, axis=1)
return U, singular_values, eigen_vectors
if __name__ == '__main__':
# 例一:普通矩阵
A = np.array(
[
[0, 1],
[0, -1]
]
)
# 例二:对称矩阵
# A = np.array(
# [
# [0, 1],
# [1, 3/2]
# ]
# )
U, S, V = svd(A)
print("我们实现的算法结果:")
print(U, "\n", S, "\n", V)
print("\n")
print("调用库函数的计算结果:")
# 调用api核对
U2, S2, V2 = np.linalg.svd(A)
print(U2, "\n", S2, "\n", V2)
对普通矩阵\(\left(\begin{matrix}0 & 1 \\0 & -1\end{matrix}\right)\)运行该算法的结果为:
我们实现的算法结果:
[[ 0.70710678 0.70710678]
[-0.70710678 -0.70710678]]
[1.4142135623730951, 0.0]
[[0. 1.]
[1. 0.]]
调用库函数的计算结果:
[[-0.70710678 -0.70710678]
[ 0.70710678 -0.70710678]]
[1.41421356 0. ]
[[-0. -1.]
[-1. 0.]]
可以看到结果基本符合。此处矩阵\(\left(\begin{matrix}0 & 1 \\0 & -1\end{matrix}\right)\)的奇异值为0.41421和0。此处我们发现普通矩阵的奇异值可以为0。
对对称矩阵\(\left(\begin{matrix}0 & 1 \\1 & \frac{3}{2}\end{matrix}\right)\)运行该算法的结果为:
我们实现的算法结果:
[[-0.4472136 0.89442719]
[-0.89442719 -0.4472136 ]]
[2.0, 0.5]
[[-0.4472136 -0.89442719]
[-0.89442719 0.4472136 ]]
调用库函数的计算结果:
[[-0.4472136 -0.89442719]
[-0.89442719 0.4472136 ]]
[2. 0.5]
[[-0.4472136 -0.89442719]
[ 0.89442719 -0.4472136 ]]
可以看到结果基本符合。此处矩阵\(\left(\begin{matrix}0 & 1 \\0 & -1\end{matrix}\right)\)的奇异值为2和0.5。此处我们发现,对称矩阵的奇异值必为正,不可能为0。
(2)奇异值的应用1:推荐系统
在推荐系统中,我们常定义用户-评分矩阵,表示用户对商品的打分,这个矩阵我们称为共现矩阵。
而这就迫切地需要我们设计矩阵分解算法,为每一个用户和视频生成一个隐向量,将用户和视频定位到隐向量的表示空间上,并满足距离相近的用户和视频表示兴趣特点接近。
在推荐系统的应用场景下,我们企图使用矩阵分解算法将\(m\times n\)维的共现矩阵\(\bm{R}\)分解为\(m \times k\)维的用户矩阵和\(k*n\)维的物品矩阵(的转置)相乘的形式。其中\(m\)是用户数量,\(n\)是物品数量,\(k\)是隐向量。\(k\)的大小决定了隐向量表达能力的强弱。\(k\)越小,隐向量包含的信息越少,模型的泛化程度越高;反之,\(k\)越大,隐向量表达能力越强,泛化程度相应降低。此外,\(k\)的取值还与矩阵分解的求解复杂度直接相关。应用中,\(k\)的取值要经过试验多次找到一个推荐效果和工程开销的平衡。具体的形式如下图所示:
采用什么方法来进行矩阵分解呢?由矩阵分析的知识可得,特征值分解只能作用于方阵,显然不适合于分解用户-物品矩阵。我们在这里采用矩阵的奇异值分解以得到用户和物品的隐向量。
已知\(\bm{M}\)是矩阵\(m\times n\)的矩阵,则一定存在一个分解\(\bm{M} = \bm{U}diag(λ_1, λ_2,..., λ_n)\bm{V}^T\),其中\(U\)是\(m*m\)的正交矩阵,\(V\)是\(n\times n\)的正交矩阵,\(diag(λ_1, λ_2,..., λ_n)\) 是 \(m \times n\)的对角阵。 我们取对角阵 \(diag(λ_1, λ_2,..., λ_n)\)中较大的\(k\)个元素做为隐含特征,删除\(diag(λ_1, λ_2,..., λ_n)\)中的其他维度及\(U\)和\(V\)中对应的维度。矩阵\(M\)被分解为\(M=U_{m*k}diag(λ_1, λ_2,..., λ_k)V_{k*n}^T\),至此完成了隐向量维度为\(k\)的矩阵分解。 如果我们调用np.lialg.svd()函数接口,那我们可以将奇异值分解表述如下:
import numpy as np
if __name__ == '__main__':
M = np.array(
[
[0, 4.5, 2.0, 0],
[4.0, 0, 3.5, 0],
[0, 5.0, 0, 2.0],
[0, 3.5, 4.0, 1.0]
]
)
U, S, V_T = np.linalg.svd(M)
k = 2 # 取前2个奇异值对应的隐向量
# 分别打印物品向量和用户向量
Vec_user, Vec_item = U[:,:k], V_T[:k, :].T
print(Vec_user, "\n\n", Vec_item)
该算法对运行结果为:
[[-0.55043774 0.1361732 ]
[-0.26216705 -0.86775439]
[-0.52483774 0.4552962 ]
[-0.5939967 -0.1454804 ]]
[[-0.12135946 -0.63908086]
[-0.83093848 0.43821815]
[-0.50855715 -0.61619448]
[-0.19021762 0.14087178]]
可以看到我们由共现矩阵成功得到了用户向量和物品向量。
然而,运在推荐系统中的传统奇异值分解存在两点重大的缺陷:
- 奇异值分解要求原始共现矩阵是稠密的,而互联网场景下用户非常少,用 户-物品的共现矩阵非常系数。如果使用 SVD,就必须对缺失的元素值进行填充。
- 传统奇异值分解的计算复杂度达到了\(O(mn^2)\)的级别,这对于商品数量动辄上百万,用户数量往往上千万的互联网场景来说根本不可接受。 所以,传统奇异值分解不适用于解决大规模稀疏矩阵的矩阵分解。因此,梯度下降法成为了矩阵分解的主要方法。这部分内容我们会在推荐系统专栏中进行讲解。
(3)奇异值的应用2:矩阵的低秩近似和数据降维
将矩阵的奇异值分解形式\(\bm{M} = \bm{U}\bm{S}\bm{V}^T\)中的对角阵进一步写成多个子矩阵的和,我们有:
\[\bm{A} = \bm{U}\bm{S}\bm{V}^T=\bm{U} \left( \begin{matrix} s_1 & & \\ & \ddots & \\ & & s_r\\ & & \\ \end{matrix} \right) \bm{V}^T \\ =\bm{U} \left( \left( \begin{matrix} s_1 & & \\ & & \\ & & \\ & & \\ \end{matrix} \right) + \left( \begin{matrix} & & \\ & s_2 & \\ & & \\ & & \\ \end{matrix} \right) + \left( \begin{matrix} & & \\ & & \\ & & s_r\\ & & \\ \end{matrix} \right) \right) \bm{V}^T \\ =s_1\bm{u}_1\bm{v}_1^T+s_2\bm{u}_2\bm{v}_2^T+... + s_r\bm{u}_r\bm{v}_r^T \]
注意,这里\(\bm{u}_1\)和\(\bm{v}_1\)是做外积,运算得到一个矩阵。 也就是说,\(m\times n\)的矩阵\(\bm{A}\)可以写成秩为1的矩阵和,即:
\[ \bm{A} = \sum_{i=1}^{r}s_i\bm{u}_i\bm{v}_i^{T} \]
我们将这个性质称为 SVD 的低秩近似性质。
在介绍 SVD 的底秩近似的应用前,我们先介绍数据降维的思想。降维的思想是将数据投影到低维空间,假设\(\bm{a}_{1},\bm{a}_2...,\bm{a}_n\)都是\(m\)维向量(在数据科学的应用中, 一般\(m\)远小于\(n\),想想为什么)。降维的目标是使用\(n\)个\(p\)维的向量替换原本的\(n\)个\(m\)维的向量,其中新向量的维度\(p<m\),同时最小化该过程引入的误差。
那么 SVD 其实天然可以用于降维。我们定义矩阵\(A\)的秩\(p\)近似,将矩阵\(A\)的奇异值分解保留前\(p\)项,即:
\[\bm{A}_p = \bm{U}_{m\times p}\bm{S}_{p\times p}\bm{V}_{p*n}^T \]
也就是其低秩近似形式保留前\(p\)项,
\[\bm{A}_p= \sum_{i=1}^{p}s_i\bm{u}_i\bm{v}_i^{T} \]
这个式子也可以看做\(\bm{A}\)的最优最小二乘近似形式,即:
\[\bm{A}_p= \underset{\bm{B}}{\text{argmin}}||\bm{A} − \bm{B}||_F \]
这里,\(\bm{B}\)的大小和\(\bm{A}\)一样,\(\bm{B} \in \bm{\R}^{m\times n}\)(但是\(rank(\bm{B})\leqslant p\)),\(F\)指F范数。这里的F范数可以推广到任意的酉不变范数\(||\bm{A} − \bm{B}||_U\),不过在常规的使用中,大家就使用\(F\)范数就够了。
矩阵最优近似是有着几何解释的。空间\(<\bm{u}_1,...,\bm{u}_p>\)由左奇异向量\(\bm{u}_1,...,\bm{u}_p\)长成,这是对于\(\bm{a}_1,...,\bm{a}_n\)的\(p\)维子空间在最小二乘意义上的最优近似,\(\bm{A}\)的列\(\bm{a}_i\)在该空间上的正交投影对应\(\bm{A}_p\)的列。换句话讲,一组向量 \(\bm{a}_1,\bm{a}_2,...,\bm{a}_n\)找到其最优的最小二乘\(p\)维子空间的投影(最小二乘后面会介绍,这里暂时理解不了也没关系)就是矩阵最优的秩\(p\)近似矩阵\(\bm{A}_p\)。
比如,我们要找到最优的一维子空间拟合数据向量\((3,2)^T,(2,4)^T,(-2,-1)^T,(-3,-5)^T\)。 4 个向量近似指向相同的一维子空间,我们想找出这个子空间,该空间能够使向量投影到子空间的平方误差和最小。然后我们找出投影向量,投影向量组成的矩阵就是我们要求的近似矩阵\(\bm{A}_p\)。
如下图所示: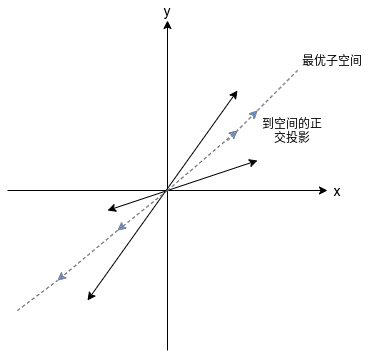
算法如下:
import numpy as np
from sklearn.decomposition import PCA
def approximation(A, p):
U, s, V_T = np.linalg.svd(A)
B = np.zeros(A.shape)
for i in range(p):
B += s[i]*U[:,i].reshape(-1, 1).dot(V_T[i, :].reshape(1, -1))
return B
if __name__ == '__main__':
# 例一:
# A = np.array(
# [
# [0, 1],
# [1, 3/2],
# ]
# )
# 例二:
A = np.array(
[
[3, 2, -2, -3],
[2, 4, -1, -5]
]
)
# p为近似矩阵的秩,秩p<=r
p = 1
B = approximation(A, p)
print(B)
#最终得到的矩阵秩
print(np.linalg.matrix_rank(B))
(注意,numpy 内置的 SVD 函数返回的是\(V^T\)而不是\(V\),我就在这儿犯过错。。。 导致后面求出来的近似矩阵不对/(ㄒoㄒ)/~~)
最终对例一矩阵\(\left(\begin{matrix}0 & 1 \\1 & \frac{3}{2}\end{matrix}\right)\)运行算法的结果如下:
[[0.4 0.8]
[0.8 1.6]]
1
该矩阵的四个列向量对应原始数据向量的投影向量。可以看到这四个向量线性相关, 且最终得到的矩阵的秩为1。
最终对例二矩阵\(\left(\begin{matrix}3 & 2 &-2 &-3 \\2 & 4 & -1 & -5 \end{matrix}\right)\)运行算法的结果如下:
[[ 1.99120445 2.59641446 -1.16885153 -3.41876737]
[ 2.73456571 3.56571418 -1.60521001 -4.69506988]]
1
该矩阵的四个列向量对应原始数据向量的投影向量。可以看到这四个向量线性相关, 且最终得到的矩阵的秩也为1。
也就是说我们的算法对这两个矩阵都达到了我们低秩近似的效果。因为降维后这两个矩阵的四个向量同属于一个一维子空间,我们只需要一个维度就可以区分这四个向量了,因此我们达到了数据降维的效果。
(3)奇异值的应用3:压缩
矩阵的奇异值分解可以用于压缩矩阵信息。我们注意到矩阵的展开式
\[\bm{A} = \sum_{i=1}^{r}s_i\bm{u}_i\bm{v}_i^{T} \]
中,每一项使用两个向量\(\bm{u}_i\),\(\bm{v}_i\),以及一个数字\(s_i\)定义。如果\(\bm{A}\)是一个\(n\times n\)矩阵,我们可以尝试矩阵\(\bm{A}\)的有损压缩,及扔掉求和后面的几项,它们具有较小的\(s_i\),也就是说对数据的存储而言显得“无关紧要”。就这样,我们可以保留前\(p\)项,将矩阵的\(p\)秩近似做为矩阵的压缩结果。\(p\)越多则近似矩阵对矩阵的近似程度越高,压缩程度越低;\(p\)越少则近似矩阵对矩阵的近似程度越低,压缩程度越高。每一项包括\(\bm{u}_i\)向量、\(\bm{v}_i\)向量和一个数字\(s_i\),总共需要\(2n+1\)个数字保存或者传输。例如,当\(n=8\)时,矩阵由\(64\)个图片定义。但是我们可以传输或者保存矩阵的第一项展开,仅仅使用\(2n+1=17\)个数字。如果大量信息可以由第一项捕捉, 例如,当第一个奇异值比其他的奇异值大得多的时候,以这种方式处理可能节省\(75\%\)的空间。
算法如下:
import numpy as np
from sklearn.decomposition import PCA
import cv2 as cv
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif']=[u'SimHei']
mpl.rcParams['axes.unicode_minus']=False
def approximation(A, p):
U, s, V_T = np.linalg.svd(A)
B = np.zeros(A.shape)
for i in range(p):
B += s[i]*U[:,i].reshape(-1, 1).dot(V_T[i, :].reshape(1, -1))
return B
if __name__ == '__main__':
img = cv.imread("chapter12.特征值和奇异值/12.4.SVD的应用/12.4.3.图像压缩/img.jpeg", flags=0)
img_output = img.copy()
# p为近似矩阵的秩,秩p<=r,p越大图像压缩程度越小,越清晰
p = 50
img_output = approximation(img, p)
fig, axs = plt.subplots(1, 2)
axs[0].imshow(img)
axs[0].set_title('原图')
axs[1].imshow(img_output)
axs[1].set_title('压缩后的图')
plt.savefig('chapter12.特征值和奇异值/12.4.SVD的应用/12.4.3.图像压缩/result.png')
plt.show()
最终图片的压缩效果: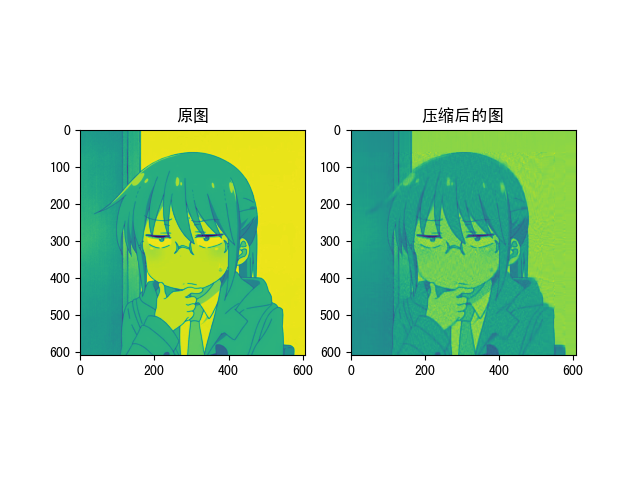
知名程序库和源码阅读建议
SVD 算法有很多优秀的开源甚至分布式的实现,这里推荐几个项目:
(1) Gensim
Gensim 是一个采用 Python 和 Cpython 实现的自然语言库,提供了很多统计自然语言处理算法的实现,也包括我们这里提到的 SVD 算法。文档地址:https://radimrehurek.com/gensim/源码地址:https://github.com/RaRe-Technologies/gensim.git
(2) Spark-MLlib
Spark 除了包含 GraphX,它还包括了机器学习库 MLlib,其中就有奇异值分解的分布式实现。文档地址:https://spark.apache.org/mllib/源码地址:https://github.com/apache/spark
参考文献
- [1] Timothy sauer. 数值分析(第2版)[M].机械工业出版社, 2018.
- [2] Golub, Van Loan. 矩阵计算[M]. 人民邮电出版社, 2020.
- [3] 深度学习推荐系统[M]. .2020