主成份分析(PCA)详解

主成分分析法（Principal Component Analysis）大多在数据维度比较高的时候，用来减少数据维度，因而加快模型训练速度。另外也有些用途，比如图片压缩（主要是用SVD，也可以用PCA来做）、因子分析等。具体怎么用，看个人需求如何，这篇文章主要解释一下PCA的原理。当然应用起来也非常简单，现在常用的语言，python、R、matlab都有直接求解PCA或者SVD的包了。

这篇文章主要想讲讲PCA的思想，当然有很多看官并不在乎这个算法的思想是什么，而仅仅急切地想要实现它，在文章最后，我们给出了R语言的实现方法，想看实现方法的可以直接跳到文章最后。 
下面我们看看PCA具体做了些什么。

我们有一组数据XX，维度是m x n，表示有 n个样本，每个样本有m个特征，即： 

现在我们想知道这个数据具体包含了哪些信息，这里可能需要引入一个大家都很熟悉的概念，方差。让我们先看其中某一维的数据，例如： x1=[x1,1,x1,2,⋯,x1,n]x1=[x1,1,x1,2,⋯,x1,n] 。如果说 x1x1 其中每一项都相等，也就是每一项都等于一个常数，那么我们认为 x1x1 并没有包含什么信息，因为它 就是一个已知的常数。所以，我们想要某一维的数据越多样性越好，这样它可以包含更多的信息，我们可以据此做出更多的推断。笼统来说，我们可以用方差来表示数据的多样性。

PCA对数据的分布其实是有一个假设的，即每一个维度上的数据都服从Gaussian分布。假设x1x1平均值是x1¯¯¯¯¯x1¯、方差是σ21σ12，令x1=[x1,1−x1¯¯¯¯¯¯σ1,⋯,x1,n−x1¯¯¯¯¯¯σ1]x1=[x1,1−x1¯σ1,⋯,x1,n−x1¯σ1]，这样x1x1就服从均值为0，方差为1的高斯分布。后面我们默认X的每一个维度都服从均值为0，方差为1 的高斯分布，即每一个维度上的数据方差都为1。这样处理过后，似乎每一个维度上的数据都包含等量的信息。

然而真实情况好像并不是这样，我们会发现有些特征能给我们带来更大的帮助，往往某一个或者两个特征能对模型产生重要的影响，而继续增加更多特征，也只会使模型在小幅度内提升。这说明有些特征能够给我们带来更多的信息，这是怎么回事呢？下面，我们来看另一个定义，协方差。

协方差是来反映数据间的相关性。有两组数据，他们的关系如下图： 
 
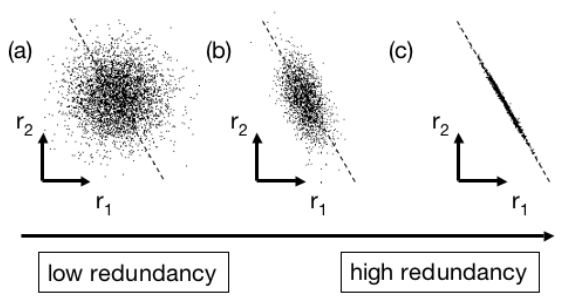
如果如图（a），则说明两组数据相关性低（或者说low redundancy）；如果如图（c），则说明两组数据的相关性高，也就是high redundancy，因为我们基本上可以认为r2=k∗r1r2=k∗r1，也就是r2r2其实是多余的。

x1=[x1,1,x1,2,⋯,x1,n]x1=[x1,1,x1,2,⋯,x1,n]，x2=[x2,1,x2,2,⋯,x2,n]x2=[x2,1,x2,2,⋯,x2,n]是服从均值为0，方差为1 的高斯分布的两组数据。我们知道方差的定义：

我们现在定义数据 x1x1 和 x2x2 的协方差： 

协方差有两个性质： 1）当且仅当 x1x1 和 x2x2 完全不相关时， σ21,2=0σ1,22=0 ；2）如果 x1=x2x1=x2 ，那么 σ21,2=σ21σ1,22=σ12 。 
现在，让我们看一个矩阵 XXTXXT ，实际上它是一个表示各维度之间方差的对称方阵， σ21,2=σ22,1σ1,22=σ2,12 ，也可以叫做协方差矩阵。 XX 的维度是 m×nm×n ， XTXT 的维度是 n×mn×m ，那么 XXTXXT 的维度则是 m×mm×m ，即： 

假设我们有一个矩阵 3×43×4 的矩阵 AA ： 

我们可以得到矩阵 AATAAT ： 

可以看到 AATAAT 是一个对称的矩阵，且每一个维度与自己的方差为1，而与其它维度的协方差则各不相同。也就是说每一个维度不仅表达了自身，这个维度所带有的信息，还表达了与其它维度的部分信息。这也就能解释，虽然每个维度的方差都为1，但是它们所包含的真实信息量是不同的。 
然而，假如我们得到一个 AATAAT 的矩阵： 

也就是说，各个维度是完全独立的，维度与维度之间的相关性为0。这样每个维度就只包含了自己的信息，我们现在就可以说第一个维度包含了矩阵 AA  59%（0.59/（0.59 + 0.29 + 0.12））的信息，第二个维度包含了29%的信息，第三个维度包含了12%的信息。

这是不是给了你一个启发，要是我能有一个数据（矩阵），它的每一个维度都是完全独立的，那么我计算出每个维度的方差，取方差最大的几个，这样我就可以用很少的几个维度，包含整个数据大部分的信息。比如上面那个例子，我用前面两个维度，就可以包含所有数据88%的信息。

这就是PCA的基本思想。然而现实中，并不是遇到的每个数据集合，它各个维度之间的方差均为0。实际上，基本上不可能存在这样的数据集合。我们收集到的数据之间或多或少都会存在关联。例如我们要预测一个人是否会发生购买行为，我们会看他浏览了了多少商品，收藏了多少商品，然而浏览与收藏之间肯定是有联系的。那么如何实现PCA呢。

矩阵当中有一个非常著名的理论，一个n×nn×n的对称矩阵AA可以表示为：A=VDVTA=VDVT。其中，VV是一个正交矩阵，DD是一个对角矩阵，除了对角线上的值可能不为0以外，其它的值均为0。

根据上面理论，对于任意一个m×nm×n的矩阵AA，AATAAT是一个m×mm×m的对称矩阵，因而AATAAT可以表示为：AAT=VDVTAAT=VDVT，即VTA(VTA)T=DVTA(VTA)T=D。也就是对于任意一个m×nm×n的矩阵AA，我们可以找到一个m×mm×m的矩阵VV，使得矩阵VTAVTA的方差矩阵VTA(VTA)TVTA(VTA)T，只有对角线上的值不为0，即矩阵各个维度之间相互独立。 

以上，PCA的思想就介绍完了。但是 VTAVTA 具体是做了什么事情呢？它对矩阵 AA 又有什么影响？让我们来看一下 VV 是一个什么样子的矩阵。

根据这个定理AAT=VDVTAAT=VDVT，实际上VV是矩阵AA中所有的特征向量构成的一个矩阵，不过这里我们并不考虑V是如何求来的，如何求得，不过是线性代数里面的一些知识。这里我们关心的是，VV是一个m×mm×m的矩阵，所以VTAVTA是一个m×nm×n的矩阵。如果我们在的VTAVTA左边乘上(VT)−1(VT)−1，矩阵又会变回AA，也就是(VT)−1VTA=A(VT)−1VTA=A。所以，实际上用VV的转置乘上AA，只是对AA做了一些行列上的变换，并没有减少任何信息，如果我们想要，我们还可以把AA变回来。这样，我们完全可以由变换后的矩阵VTAVTA，来表示原来的数据AA，且不会有任何信息损失。而且，转换后的矩阵有一个非常好的性质，就是各个维度之间相互独立，所以我们可以得到它的方差矩阵VTA(VTA)T=DVTA(VTA)T=D，是一个只有对角线上元素不为0的对角矩阵。

这样，我们就可以知道每一个维度分别包含了多少信息。假如数据的维度m，是一个非常大的值，例如10，0000，如果我们发现仅仅使用前10个维度，就能包含95%以上的信息，那么我们将很高兴用这10个维度，而舍弃掉剩下的其它维度，这相当于将数据压缩了10000倍，而并没有损失多少信息。当然这只是我们的臆想，实际情况不一定有这么好。

R实现：

#从R内置数据集iris中取前10行
> A <- as.matrix(iris[1:10,-5])
> A
   Sepal.Length Sepal.Width Petal.Length Petal.Width
1           5.1         3.5          1.4         0.2
2           4.9         3.0          1.4         0.2
3           4.7         3.2          1.3         0.2
4           4.6         3.1          1.5         0.2
5           5.0         3.6          1.4         0.2
6           5.4         3.9          1.7         0.4
7           4.6         3.4          1.4         0.3
8           5.0         3.4          1.5         0.2
9           4.4         2.9          1.4         0.2
10          4.9         3.1          1.5         0.1

#可以看到A是一个10x4的矩阵,下面我们对A进行标准化
> A <- scale(A)
> A
   Sepal.Length Sepal.Width Petal.Length Petal.Width
1     0.8237318   0.6186158     -0.46291  -0.2535463
2     0.1372886  -1.0093205     -0.46291  -0.2535463
3    -0.5491545  -0.3581460     -1.38873  -0.2535463
4    -0.8923761  -0.6837333      0.46291  -0.2535463
5     0.4805102   0.9442031     -0.46291  -0.2535463
6     1.8533965   1.9209649      2.31455   2.2819165
7    -0.8923761   0.2930285     -0.46291   1.0141851
8     0.4805102   0.2930285      0.46291  -0.2535463
9    -1.5788192  -1.3349078     -0.46291  -0.2535463
10    0.1372886  -0.6837333      0.46291  -1.5212777

#未对其进行转化前A的协方差矩阵如下，对角线上的值均为1，而协方差各异，
#因而不好估量每个维度所包含的信息
> var(A)
             Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length    1.0000000   0.7872066    0.6002160   0.3770977
Sepal.Width     0.7872066   1.0000000    0.5191385   0.6787563
Petal.Length    0.6002160   0.5191385    1.0000000   0.5216405
Petal.Width     0.3770977   0.6787563    0.5216405   1.0000000

#利用内置svd函数队矩阵t(A)进行分解，t(A)即A的转置，转置后变成4x10的矩阵,
#与文中一致。其中，得到的矩阵s$u即为文中的矩阵V 
> s <- svd(t(A))
> s$u
           [,1]        [,2]        [,3]       [,4]
[1,] -0.5088012  0.60992283 -0.19490104 -0.5754381
[2,] -0.5486817  0.02313419 -0.49127967  0.6760603
[3,] -0.4747485  0.08790411  0.84594304  0.2264225
[4,] -0.4633397 -0.78723048 -0.07098059 -0.4006822

#利用t(V)%*%t(A)原矩阵进行转换,再看一下转换后矩阵的协方差矩阵，这里保留两位小数
> AA <- t(s$u) %*% t(A)
> round(var(t(AA)), 2)
     [,1] [,2] [,3] [,4]
[1,] 2.75 0.00 0.00  0.0
[2,] 0.00 0.63 0.00  0.0
[3,] 0.00 0.00 0.52  0.0
[4,] 0.00 0.00 0.00  0.1

#可以看到，转换后矩阵各维度之间相互独立，并且可以知道每个矩阵包含了多少信息。
#假如我们取前三个纬度，则可以包含97.5%的信息，(2.75+0.63+0.53)/( 2.75+0.63+0.53+0.1)=0.975。

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60

这里我们使用R中内置的函数SVD，来实现PCA的算法。实际情况中，我们常常可以看到SVD和批PCA在一起被提到，它们之间又有什么关系。感兴趣的话，可以看看我的下一篇blog：SVD与PCA详解。