转载自：http://www.guokr.com/blog/444081/
自古计算圆周率是数学界一项流行运动，各大数学家争相破记录以名垂青史。想象有人为圆周率15年如一日地算，算的不是圆周率而是寂寞啊！
自有圆周率，计算
比的是数学；后有现代数学，计算比的是寂寞；自从有了计算机，计算变成程序员们（另一种）练手的健康活动：锻炼编程技术之余可比肩历史伟人，看官也来一发吧！不懂数学没关系，计算圆周率并不需要多少数学知识，你需要的只是一些编程基础、一点数据结构知识，还有本文准备给你的：算法。
（题外话：如果本文中所有公式都显示成叉，说明你在使用古董级浏览器，请升级……）
========【摘要】========
1）本文介绍编程计算圆周率的主流算法，从简单到复杂任君选择，目的是让读者看完能动手算一把。
2）不涉及具体的编程语言技术，也不涉及数学证明。
3）所有算法都不限编程语言，你可以用你最擅长的语言来实现。不过在科学计算领域，C/C++兼顾性能和便捷，依然是首选，文中少量示例都用C/C++。
4）即使你没时间动手，本文也可带你浏览一下科学计算王国。
【读懂本文，你需要一点点的……】
1）编程基础
2）数据结构基础
3）高等数学基础
========【概述】========
千言万语不如先来一发：
#include <stdio.h>
int main()
{
double p = 3;
for (int i = 2 ; i <= 100000 ; i+=4)
{
p += 4 / (double(i)*(i+1)*(i+2));
p -= 4 / (double(i+2)*(i+3)*(i+4));
}
printf("pi=%.14f\n", p);
return 0;
}
请把以上代码拷进C语言开发环境里运行，瞬间出结果如下：
pi=3.14159265358979
恭喜！14位小数无一错误！你已经破了公元1400年的纪录！祖冲之那7位小数真的弱爆啦！……只是开了个玩笑，算圆周率前请先拜大神，可保佑不溢出：
祖冲之（ 公元429年4月20日─公元500年），我国杰出的数学家，科学家。曾计算出圆周率7位小数，是之后近1000年的世界纪录保持者。
凡是讨论算法，必谈时间复杂度。祖冲之的年代，圆周率源自几何也算以几何，原理是在圆周割成多边形来计算周长，称为几何算法，时间复杂度高、计算量极大。经过现代数学和计算科学的发展，圆周率计算方法变得非常高效，例如上面的C语言例子用的是以下无穷三次级数：
不用计算机，笔算也能算出好几位，时间复杂度是O(10^(N/3*2))（N是十进制位数，下同），但仍不足以计算成千上万位。另外，例子中用double（双精度浮点数）类型来计算圆周率，但编程语言支持的浮点类型最多就十几、二十位几小数，显然上面那种简单的程序无法算出更精确的pi。为了让计算机处理超长的小数，我们要用很大的数组来储存小数（称为【高精度计算】），并为此实现专门的加减乘除、开方算法。本文后续将详细介绍高性能的圆周率计算方法和与之配套的高性能高精度计算。
圆周率计算方法极多，但不是每种都能高效实用。现代圆周率计算方法主要有两种：
第一种方法基于pi可以分解成一组幂级数和，例如等一下我会介绍的贝利－波尔温－普劳夫公式：
非常简单有效的算法，用最基本的高精度四则运算即可实现，没有高精度的分母，没有两个大数相乘，更没有开方，时间复杂度是O(N^2) ，推荐从这个上手。
第二种方法包括稍后介绍的高斯-勒让德算法，依靠上世纪60年代发明的神器快速傅里叶变换而达到时间复杂度O(N(logN)^2)，位数多时优势明显，是世界纪录和众多圆周率计算软件的算法，包括著名的SuperPI，但用到的高精度计算技术稍复杂。
========【高精度计算基础】========
在圆周率计算和各种科学计算中，都用数组来储存一个很长的小数（或者超大的整数，或小数点前后都有很多位）。例如，下面表示用【高精度数组】a储存的圆周率，数组每个单元保存8位十进制小数：
等同于：
其中100000000是进制。一般地，小数A用高精度数组a基于d进制储存可表示为：
计算机的储存空间有限，所以n是一个有限的整数。进制d一般是10或者16的整数次幂，其中16整数次幂的方法对储存的利用率更高、进位计算更快速，但输出时转成十进制需要很大的计算量（O(N^2)），有时甚至比计算pi本身更耗时间。
对高精度数组表示的小数进行各种加减乘除运算，称为【高精度计算】。例如，最简单的高精度计算是加法，把两个高精度数组对位相加，即可得出两个小数的和高精度小数：
代码看起来是这个样子的：
for (k=0 ; k<n ; k++)
c[k]=a[k]+b[k];
如果结果中若干项超过进制d，则对其进行进位运算。C语言进位的代码看起来是这个样子的：
for (k=n-1 ; k>=0 ; k--)
if (a[k] > d)
{
a[k-1]=a[k]/d;
a[k]=a[k]%d;
}
进位可能也造成a[k-1]也超过了d，于是进位从最低位a[n]一直到最高位a[0]反向遍历执行。
减法（或者负数加法）的原理也类似，对位相减后执行退位操作（略）。
【高精度乘法】基本计算方法是【卷积】，小学时教我们的竖式乘法本质也是卷积。所谓卷积，就是多项式每一项都与另一个多项式的每一项相乘、累加：
小学教的竖式乘法就是卷积，被乘数和乘数各位两两相乘、相加、进位：
高精度数组a和b相乘的数学表达是：
所以C的每一项是：
上面的式子看傻了没关系，高等数学就是喜欢把简单的东西写得很复杂……其实原理极简单，代码看起来是这个样子的：
for (k=0;k<n;k++)
for (j=0;j<m;j++)
c[k+j]+=a[k]*b[j];
同样要进行进位操作。两个n位精度的小数相乘，虽然结果有2n-1项，但其实精度只有前面n项是准确的，后n-1项丢弃或不予计算。卷积的时间复杂度是O(nm)。
如果加减乘对你来说都没有压力，那【高精度除法】也许能给你带来一些麻烦。高精度除法基本算法就是小学教的竖式除法：试除一位x、计算【被除数-（x×除数）】得余数，余数进行退位运算后作为被除数重复上面的过程。如果除数是一个整数，这个并不会很困难，试除用的是被除数的前几位除以除数。但如果除数也是高精度数组就有点麻烦了，除数也要用前几位作为试除位来试除。这种基本除法算法时间复杂度是O(nm)，n是结果精度，m是除数精度，与被除数精度无关。实际上这种代码实现起来比后面的高性能计算方法更长更麻烦（因为后面介绍的方法把除法转化成乘法，可直接调用乘法的代码），所以这里略去。
========【高精度数制的选择】========
在你实现高精度运算时，需要决定数制，或写出兼容任何数制的代码（但这并不好）。所谓数制，就是我们平时使用的十进制、十六进制。唯一不同的，高精度的数制不是其显示出来的数制，而是其每个单元储存数据的上限。例如规定高精度10000进制，表示一个单元达到或超过10000时，应该减去10000，并对其高一位的单元加1（进位），或是一个单元小于0，则加上10000，其高一位减1（退位）。
一般我们选用10或16的整数次幂作为高精度的数制，两者各有优缺点。10整数次幂的数制运算完后无需转数制可直接输出十进制的结果；而16整数次幂进制进位速度高，只需要用编程语言的位运算符，性能远好于取模、除法运算，而且下面的BBP公式和十六进制是绝配，通用所有数制的程序几乎不可能利用有这些优点，我们没必要写出通用的程序。
因此，有时我们可能选择用16整数次幂进制计算，然后转成十进制输出。转换算法很简单，对于任意一个高精度16整数次幂进制的小数，重复下面的步骤：
）
以上计算每一个循环能输出n位，总时间复杂度是O(N^2)：这个是个大问题，超过了高斯-勒让德算法的时间复杂度，所以如果用16整数次幂进制跑高斯-勒让德算法然后再转十进制会得不偿失，转换的速度甚至比计算更慢。幸好，这个计算易于实现多线程并行运算，很容易充分发挥CPU超过4个线程的性能。
现在你已经学会了基本的高精度计算，用BBP来算已经难不倒你了。
========【贝利－波尔温－普劳夫公式（BBP公式）】========
BBP公式是圆周率计算的众多无穷幂级数方法之一，均具有O(N^2)的时间复杂度，优点是实现简单、极容易实现多线程并行运算、内存使用效率高，使用最为广泛。
其计算过程是这样的：
其中每个方块都表示一个高精度数。留意左边1/16^k越来越少，总有某一项之后小于你设置的高精度数组的精度，之后就不用计算了，可输出结果。计算过程只有高精度加法、减法，高精度数乘除非高精度整数。计算总项数n正比于计算精度，每轮计算涉及的高精度计算时间复杂度都是O(N)，所以总复杂度是O(N^2) 。
刚才说，BBP和十六进制是绝配，不只是因为免去左边除以16的O(N)除法，还因为BBP公式在十六进制计算时可以只计算其中某些位而无需计算前面的未，例如从n位计算到n+m位，时间复杂度是O(n*m)。基于这个特点，BBP不是圆周率幂函数计算公式最高效的一个，却最适合多线程并行和分布式计算，还能用来验算其它算法算出来的十六进制结果。考虑到一点跑题，不在这里详述，有兴趣可看看维基百科中相关的方法（较简单）。
========【高斯-勒让德算法（GLA）】========
BBP之类的O(N^2)方法很简单，但在世界纪录级别（万亿位）难等大雅之堂，我们需要的一些O(N logN)级别的神器。其中最简单的是GLA，SuperPi用的就是这个。
GLA写出来很简单。
初始化：
迭代：
最后计算pi为：
其中，除了p外，其余（a，b，t，pi）都为高精度数，例如计算100万位圆周率，则这4个高精度数都是100万位。迭代过程中，a和b会不断接近，迭代结束条件是a和b的差距超过其本身精度的一半（例如计算100万位，那结果a和b第一个不同的位在50万位后即可结束迭代）。p是普通的整型。
每迭代一次，a和b的差的数量级增加一倍，所以迭代次数为O(log N)，计算100万位的圆周率约需要迭代20次。
GLA难点和主要计算量在高精度乘法和开方，乘法和开方的性能决定GLA的性能。要使GLA的时间复杂度达到O(N (log N)^2)，你需要下面的算法。
========【高精度乘法-快速傅里叶变换】========
基本的高精度乘法用卷积，时间复杂度O(nm)，用它的话我们GLA的O(N (log N)^2)就报销了。我们要祭出神器中的神器：FFT——快速傅里叶变换。有了FFT，对大数乘法、除法、开方通通有了过往不可想象超高性能，Pi的位数疯狂增长。
尽管我尽了最大努力，但本节仍是这篇文章最难读懂的部分，你可能会一头雾水——没办法，神器自有神器的架子，在我自行参透前网上几乎没找到清晰的讲解，所以写这部分结合了我自己的经验，着重解释最难理解的部分，并使用大量的图示，尽可能让过程更直观。尽管看起来很复杂，但代码核心部分也只有10-15行，因为其有着惊为天人的对称性，体现着让人叹为观止的数学美。
【傅里叶变换】和【快速傅里叶变换】：【傅里叶变换】本来不是用来算乘法的，而是用来分解波（例如声音或者电磁波），而用来做卷积则是上世纪自有计算机后发现的。傅里叶变换将一组复数通过一系列计算转换成另外一组复数，转换前后复数个数一样，转换后的每个复数都和转换前每个复数相关。【快速傅里叶变换】泛指可以在O(N logN)时间复杂度内完成傅里叶变换的算法。根据卷积定理，两个多项式的卷积的傅里叶变换等于其各自的傅里叶变换对位相乘，如果结合快速傅立叶变换，就可以在O(N logN)的时间复杂度内完成高精度乘法。本文只介绍算法而不论数学原理和证明，其实我还没搞懂我会告诉你吗？
【算法总体流程】假设要对高精度数组A和高精度数组B以快速傅里叶变换计算卷积，总体流程如下：
如图：
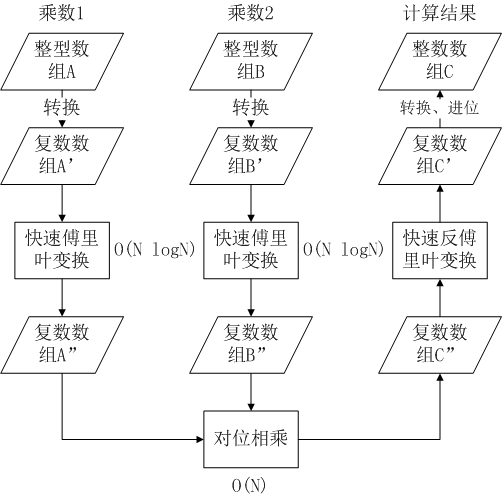
其中，转换就是普通的数据类型转换，整数转成一个虚部为0的复数，或者复数舍弃虚部，实部四舍五入成整数。
“快速反傅里叶变换”（IFFT）是“快速傅里叶变换”（FFT）的逆过程。事实上由于数学上的对称性，两者几乎是一样的，核心代码只用一套，无需分别写。
快速傅里叶变换有多种具体算法，以下介绍最简单的“库利－图基快速傅里叶变换”【C-T FFT】。
【转换】C-T FFT要求上图中所有复数数组统一大小，且为2的整数次幂，不小于相乘两个数的长度和，所以计算前需要先补0。假设计算1.11×2.22，高精度数组是十进制，1.11和2.22都是3个单元的精度，3+3=6，不小于6的2的整数次幂是8，所以整个流程看起来是这样的（用(a,b)表示复数a+bi，下同）：
【转换精度问题】复数使用两个浮点数表示，计算机支持的64bit浮点数一般只有54bit的有效位数（GCC支持96bit long double类型并不通用）。假设高精度整数数组每个单元是 x bit，即不大于
进制，FFT长度是
，那么为了防止精度不足而造成计算错误，x和N必须满足：
这个条件相当苛刻，意味着 x 得不超过16，即不超过2^16=65536进制。如果用10整数次幂计算，不能超过10000进制。所以当你用的数制较大，转复数数组时必须拆开到65536进制或10000进制。当高精度数组尺寸达到约2^24时，还得进一步下降到256进制和100进制。
【结果精度问题】用n位d进制表示一个无穷小数时，误差不超过
，那么两个小数相乘后，结果误差不超过
（和加减法一样），仍然是n位，超过n位即使算出来也是不准确的，可以舍去。证明很简单，略。
【FFT 和 IFFT】刚才提到，傅里叶变换和反傅里叶变换有漂亮的对称性，IFFT只需在FFT前后再加一点东西：
其中，共轭就是复数数组中所有单元的虚部取负值（高中数学呀），归一化就是全部复数除以N（数组的大小）。由于我们计算高精度乘法时，输出结果虚部一定是0，所以最后一个共轭计算可以节省。
【FFT过程】公式神马的最讨厌了，要说清楚FFT，千言万语不如一张图：
即使你没看明白也一定能感受到这图的震撼，它有着各种完美的周期性和对称性。留意从顶上的输入数组到底下输出结果数组有很多连线，输入的任意单元和输出的任意单元之间有且只有一条通途。
其中W(k,N)是“旋转因子”，表示模为1，-k/N个圆周角的复数，即：
(*)所谓位元反转排序就是把数组单元的序数k的N位二进制全部位取反，例如：
4的二进制是100，把所有位反过来是001，是1的二进制，所以x4和x1交换。
N=8时，0、5等因为位元反转后仍是自身，所以x0、x2、x5、x7无需换位。
请细细观察图中的规律，直到你有点头绪了，看看下面我归纳的规律：
一、对于N=2^p的FFT，有p轮计算。
二、每一轮计算都两两组合。
三、决定如何组合两个单元的规律在于两个单元的序数的二进制，例如第二轮组合的是：
四、组合右边的单元乘以W(k,N)，留意到 k 的规律，和组合的两个数密切相关，是两数【异位】右边部分的左移b位，第1轮b=2，第2轮b=1，第3轮b=0。举例：
五、组合的两个单元执行交叉加减法，左'=左+右，右'=左-右
算法都在上面了，你可以动手写程序了。你需要看清楚图中每一轮转换的规律，写出适应任意N=2^p的计算代码。
【优化】基于大数运算来计算圆周率的算法大部分时间都用来FFT，所以提高FFT性能是关键。下面是一些优化思路，需要一定的编程功底，可根据你自己的能力选择使用哪些。
【优化1：旋转因子缓存】计算中重复使用旋转因子，计算机计算cos和sin的速度较慢，可将其一次计算并保存在数组中，计算时直接提取，在整个计算过程中会被重复调用，可有效节约计算时间。
【优化2：CPU指令集优化】FFT中涉及大量复数运算，SSE系列指令集非常适合对其进行优化。VC和GCC编译器都有提供库（但不统一）来直接调用SSE指令集，经在VC中测试，对32位编译的程序性能提升达3倍，而64位编译程序提升没那么多但仍然显著，可能64位编译时已经有一些智能的方法自动调用SSE。
【优化3：多线程优化】FFT算法是典型的分治算法，非常适合多线程并行运算。注意上面的计算流程图，除了第三轮计算，前面的计算是左右独立的，意味着前两轮可以建立2个线程分别计算左右部分，两者汇合（Join）计算最后一轮。同理，第一轮可以分成4个线程计算，计算完毕后两两汇合成两组计算。当N非常大，可以很容易将计算量分摊到所有CPU线程中，例如N=1024=2^10，为10轮计算，CPU有4个线程，则前8轮分成4个线程计算，第9轮汇合成2个线程计算，最后第10轮一个线程完成计算。
========【高精度除法/开根号：牛顿迭代法】========
费了九牛二虎之力搞掂了FFT，我们的高速算pi已经几近成功了，接下来我们用牛顿迭代法把除法和开方转成乘法，那就功德完满了。
我们先来复习一下牛顿迭代法：牛顿迭代法可以用来计算任意2阶可导的函数f(x)=0的数值解。
假设方程
在
附近有一个解，那么使用迭代公式：
那么x序列将越来越接近方程的解，每迭代一次有效小数增加一倍。
对于除法和开方，f(x)有不只一种，要找到适当的f(x)，使迭代过程中没有除法和开方，只有乘法。
【除法算法】计算a/b，先用牛顿迭代计算1/b，f(x)是：
迭代式：
【取倒数算法】
迭代结果再乘以a，即为a/b。
由于牛顿跌代法对任意一步的误差都不敏感，你可以取任意初始值来计算，不过最好的方法是将b的前几个单元换算成浮点数，计算1/b然后开始迭代。由于开始迭代时精度低，无需用太高精度的数组，b也截断到较低精度，然后每迭代一次的精度增加一倍，直到达到指定的精度。如此，每迭代一次的开销增加一倍，总计算量的一半在进行最后一轮的迭代。最后一轮迭代有2次乘法，再加上最后计算一个乘法，总计算量约是同样精度乘法的5倍，时间复杂度依然是O(N logN)。
【开方算法1】计算a的开方：
迭代（这个方法不好，看下面的【开方算法2】）：
虽然我们已经能算除法了，但这就成了迭代中的迭代，让人不舒服。
【开方算法2】
先计算：
迭代 x 的f(x)是：
迭代式：
迭代完成后再用上面【取倒数算法】计算1/x即为
计算方法与除法很相似，你甚至可以重用大部分代码。一次迭代3次乘法，开始时只需要截断到低精度计算并逐次精度加倍，总迭代计算量是6个乘法，加上取倒数是4个乘法，总共是10个乘法的计算量，时间复杂度依然是O(N logN)。测试证明【开方2】比【开方1】快20%左右，而且避免了迭代套迭代，推荐使用。
========【写在最后】========
本文主要介绍了这几个计算圆周率相关的要点：
事实上如果你掌握了高性能高精度计算方法，可以挑战一些更有难度但更快的算法。
目前世界纪录是用巨型机跑出来的10万亿位，如果用SuperPI和普通CPU计算的话，它要吃掉600T的内存和耗时20年。
笔者使用OpenCL编程开发的程序可使用GPU进行计算，可在3秒内完成一百万位计算，参见：http://www.guokr.com/blog/483329/
