浅谈对梯度下降法的理解

浅谈梯度下降法

如果读者对方向导数和梯度的定义不太了解，请先阅读上篇文章《方向导数与梯度》。

前些时间接触了机器学习，发现梯度下降法是机器学习里比较基础又比较重要的一个求最小值的算法。梯度下降算法过程如下：

1）随机初始值；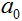

2）迭代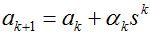，直至收敛。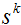表示在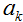处的负梯度方向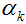，表示学习率。

在这里，简单谈一下自己对梯度下降法的理解。

首先，要明确梯度是一个向量，是一个n元函数f关于n个变量的偏导数，比如三元函数f的梯度为(f_x,f_y,f_z)，二元函数f的梯度为(f_x,f_y），一元函数f的梯度为f_x。然后要明白梯度的方向是函数f增长最快的方向，梯度的反方向是f降低最快的方向。

我们以一元函数为例，介绍一下梯度下降法。

设f(x) = (x-1)²+1/2，

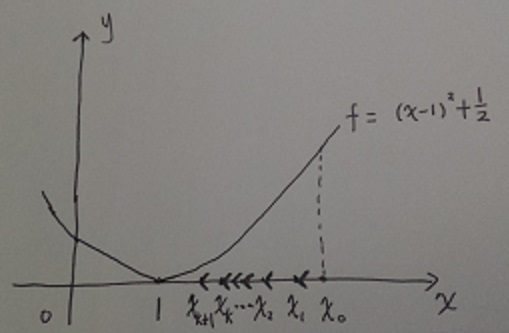
上图给出了函数f的图像和初始值x₀，我们希望求得函数f的最小值，因为沿负梯度方向移动一小步后，f值降低，故只需x₀沿着负梯度方向移动一小步即可。

而f在点x₀的导数大于0，从而f在点x₀的梯度方向为正，即梯度方向为f’(x₀)，故由梯度下降法可知，下一个迭代值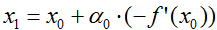，也就是说x₀向左移动一小步到了x₁，同理在x₁点的导数同样大于零，下一次迭代x₁向左移动一小步到达x₂，一直进行下去，只要每次移动的步数不是很大，我们就可以得到收敛1的解x。

上述证实了我们对分析（蓝色倾斜字体）的验证。

同样，如果处置选在了最小值的左边，即如图所示：

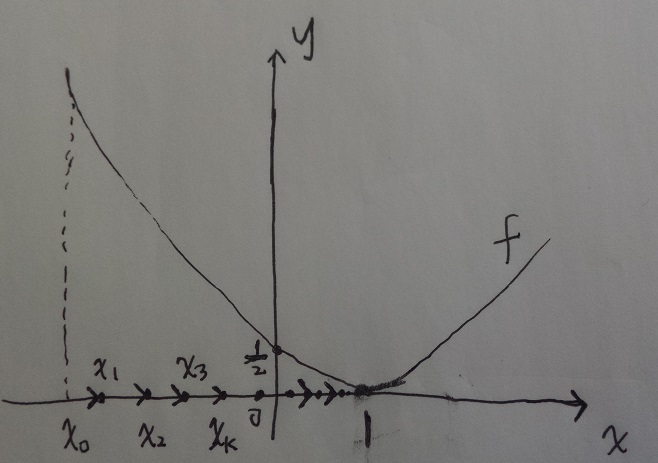
由于f’(x₀)<0，所以梯度方向为负，负梯度方向为正，故需将x₀沿负梯度方向移动一小步，即向右移动一小步，这样使得f值更小一些。或用梯度下降法迭代公式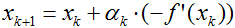，依次我们可以得到如图所示的x₁,x₂,...,x_k,...，直到收敛至最小值。

对于二元函数，我们也可以通过实例验证梯度下降法的合理性：

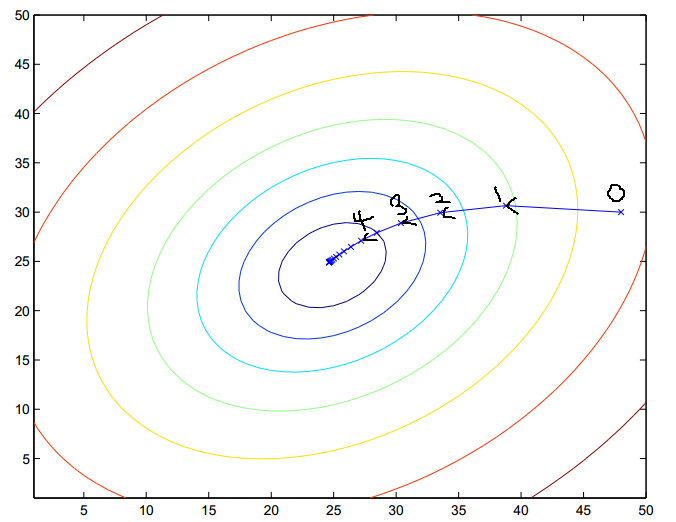
在每次得到一个点(x_k,y_k)时，我们需要计算(f_x(x_k),f_y(y_k))，这个方向表示梯度f增长最快的方向，-(f_x(x_k),f_y(y_k))表示梯度下降最快的方向，故只需将(x_k,y_k)沿着-(f_x(x_k),f_y(y_k))这个方向移动一小步，就可以减少f的值，直至收敛到最小值，如上图所示。

谈几点梯度下降法需要注意的地方，也是自己对梯度下降法的理解：

1）梯度下降不一定可以收敛到最小值。

梯度下降法是收敛到局部最小值，不一定可以收敛到全局最小值。

比如：

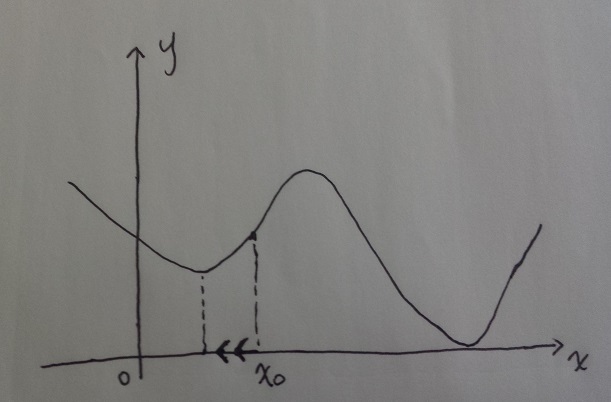
我们初始值选择了如图的x₀，由于f在点x₀的导数大于0，梯度方向向右，负梯度方向向左，从而x₀向左移动，逐渐收敛到了局部最小值，而不能收敛到全局最小值。

2）学习率的大小要适中。

学习率太小，每次移动步长太小，收敛太慢，这个比较容易理解。

学习率太大，每次移动步长大，可能导致不收敛，这里用一个图来表示一下：

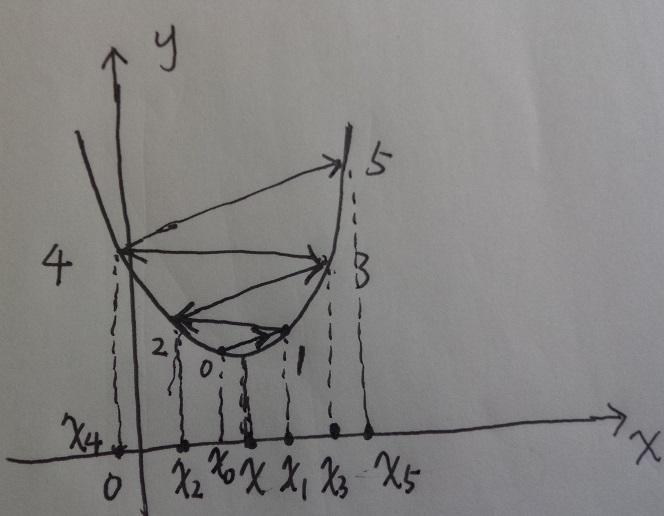
由于距离最小值点越远，导数越大，从而导致步长越来越大，不会收敛。

3）不一定选择负梯度方向，只要是值下降的方向即可。

在每一次迭代选择方向时，我们只要选择与梯度方向夹角小于90度的向量的反方向就可，不一定要选择负梯度方向。但由于，满足这样条件的向量不太容易求出，我们就选择了与梯度方向0度的向量的反方向（负梯度方向），而且这个方向函数值减少的更快，更快的收敛，故是个不错的选择。

4）求最大值的梯度上升法。

f的梯度方向是f的值增长最快的方向。我们每次沿负梯度方向移动一小步可以逐步收敛到局部最大值，因此我们每次沿梯度方向也可以得到函数f的局部最大值。迭代公式为：

，

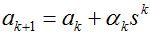这里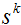表示在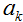处的梯度方向，与梯度下降法的含义不同。

本文由作者结合自己对梯度的理解写出，希望对大家有所帮助，敬请阅读、指正。