版权声明

原创作品，整理不易，转载请标明出处。本篇推送更详细的内容介绍，可参见本人微信公众号“优化与博弈的数学原理”，公众号二维码参见文末。或参见以下网址：优化理论 | Time-Sharing Condition

编者按

OFDM系统中的功率分配问题是通信领域中的研究热点。本文重点考虑了面向同频干扰场景下OFDM系统的功率分配问题，该问题通常被建模为含复杂多耦合变量的非凸优化问题，因此现有方法难以求得该问题的最优解（即存在对偶间隙）。本篇推送通过文献阅读及相关调研，学习并记录了基于 Time-Sharing Condition 及 General Duality Theory 的求解思路，该方法可有效解决同频干扰场景下OFDM系统功率分配问题的非凸性，相关文献证明了在特定的条件下，该方法可以完全消除对偶间隙。

一、问题描述

问题1：无干扰场景下的信道容量最大化

先让我们回顾一下MIMO无线通信领域的一个常见问题，受限功率下最大化信道容量问题，即注水问题：
P 1 : min ⁡ p ∑ n = 1 N l o g ( 1 + p n σ n 2 ) s . t . { p ⪰ 0 ∑ n = 1 N p n ≤ P \begin{align} {P_1:}&\mathop{\min}_{p}{ \sum\limits_{n=1}^N log(1+\frac{p_n}{\sigma_n^2}) } \nonumber \\ &s.t. \begin{cases} p \succeq 0 \nonumber \\ \sum\limits_{n=1}^{N}p_n \leq P \nonumber \end{cases} \end{align} P1​:​minp​n=1∑N​log(1+σn2​pn​​)s.t.⎩ ⎨ ⎧​p⪰0n=1∑N​pn​≤P​​

其中，目标函数表示包含 N N N 个并行子信道的系统信道容量（如OFDM系统）。 p = [ p 1 , p 2 , … , p N ] p=\left[ p_1, p_2, \dots, p_N \right] p=[p1​,p2​,…,pN​] 表示信号功率且为决策变量， p n p_n pn​是子信道 n n n中的信号功率， σ n 2 \sigma_n^2 σn2​是子信道 n n n中的噪声功率。

问题2：有干扰场景下的信道容量最大化

今天主要想介绍，在存在干扰的情况下，如何求解其优化问题，并确保对偶间隙为0。 仍然考虑K个用户，N个子信道的优化问题，如下：
P 2 : min ⁡ p ∑ k = 1 K w k ∑ n = 1 N l o g ( 1 + p k n σ k n + ∑ j ≠ k α j k n p j n ) s . t . { p k n ≥ 0 ,    ∀ k , n ∑ n = 1 N p n k ≤ P k ,    ∀ k \begin{align} {P_2:}&\mathop{\min}_{p}{ \sum\limits_{k=1}^K w_k \sum\limits_{n=1}^N log(1+\frac{p^n_k}{\sigma_k^n+\sum_{j \neq k}\alpha_{jk}^n p_j^n)} } \nonumber \\ &s.t. \begin{cases} p_k^n \geq 0, \ \ \forall k,n \nonumber \\ \sum\limits_{n=1}^{N}p_n^k\leq P_k, \ \ \forall k \nonumber \end{cases} \end{align} P2​:​minp​k=1∑K​wk​n=1∑N​log(1+σkn​+∑j=k​αjkn​pjn​)pkn​​s.t.⎩ ⎨ ⎧​pkn​≥0,  ∀k,nn=1∑N​pnk​≤Pk​,  ∀k​​
注1：上述问题摘自 Multiuser DSLs 场景，与 OFDM 类似，后文不予区分 DSL 与 OFDM 的区别；
注2：为方便符号表述， σ k n \sigma_k^n σkn​表示噪声功率，这里不写平方了。

下文，我们将回顾问题1的经典求解方法[1]，并详细介绍针对问题2的研究现状、理论证明及求解方法。

二、问题1的求解方法（基础回顾）

由于问题1满足 Slater 条件，故具有强对偶性，且其 Lagrange 函数为：

L ( p , λ , ν ) = − ∑ n = 1 N l o g ( 1 + p n σ n 2 ) − λ T p + ν ( ∑ n = 1 N p n − P ) L(p,\lambda,\nu)=-\sum\limits_{n=1}^{N}log(1+\frac{p_n}{\sigma_n^2}) -\lambda^Tp+\nu(\sum\limits_{n=1}^{N}p_n-P) L(p,λ,ν)=−n=1∑N​log(1+σn2​pn​​)−λTp+ν(n=1∑N​pn​−P)
计算其KKT条件：
∂ L ( p , λ , ν ) ∂ p n = − 1 1 + p n σ n 2 1 σ n 2 − λ n + ν = 0 \frac{\partial L(p,\lambda,\nu)}{\partial p_n}=\frac{-1}{1+\frac{p_n}{\sigma_n^2}}\frac{1}{\sigma_n^2}-\lambda_n+\nu=0 ∂pn​∂L(p,λ,ν)​=1+σn2​pn​​−1​σn2​1​−λn​+ν=0
可得：
λ n = ν − 1 p n + σ n 2 \lambda_n = \nu - \frac{1}{p_n+\sigma_n^2} λn​=ν−pn​+σn2​1​

• 情况1： λ n > 0 \lambda_n >0 λn​>0 且 p n = 0 p_n=0 pn​=0 ⇒ λ n = ν − 1 σ n 2 > 0 \lambda_n = \nu - \frac{1}{\sigma_n^2}>0 λn​=ν−σn2​1​>0 ⇒ 1 ν < σ n 2 \frac{1}{\nu}<\sigma_n^2 ν1​<σn2​
• 情况2： λ n = 0 \lambda_n =0 λn​=0 且 p n ≥ 0 p_n\geq0 pn​≥0 ⇒ ν = 1 p n + σ n 2 \nu = \frac{1}{p_n + \sigma_n^2} ν=pn​+σn2​1​ ⇒ p n = 1 ν − σ n 2 ≥ 0 p_n=\frac{1}{\nu}-\sigma_n^2\geq 0 pn​=ν1​−σn2​≥0

因此：
p n ∗ = max ⁡ { 0 , 1 ν ∗ − σ n 2 } p_n^*=\max\{0,\frac{1}{\nu^*}-\sigma_n^2\} pn∗​=max{0,ν∗1​−σn2​}

其中，最优解 1 ν ∗ \frac{1}{\nu^*} ν∗1​ 可由下式解出：【记下式为 ( ∗ ) (*) (∗)式】
∑ n = 1 n p n ∗ = max ⁡ { 0 , 1 ν ∗ − σ n 2 } = P \sum\limits_{n=1}^n p_n^* = \max\{0,\frac{1}{\nu^*}-\sigma_n^2\}=P n=1∑n​pn∗​=max{0,ν∗1​−σn2​}=P

显然求和约束在最优解处一定为紧约束，故取等。现求解 ( ∗ ) (*) (∗) 式的方法如下：

首先，假设对任意 n n n 都有 p n > 0 p_n>0 pn​>0（即对任意 n n n 都有 1 ν − σ n 2 > 0 \frac{1}{\nu}-\sigma_n^2>0 ν1​−σn2​>0），然后找到 ( ∗ ) (*) (∗)式的解 1 ν ∗ \frac{1}{\nu^*} ν∗1​。若不存在可行解，则可得 p l ∗ = 0 p_l^*=0 pl∗​=0，其中 l = a r g m a x { σ n 2 } l=argmax\{\sigma_n^2\} l=argmax{σn2​}，再次求解 ( ∗ ) (*) (∗) 式得到 1 ν ∗ \frac{1}{\nu^*} ν∗1​ 。重复上述步骤，使得每次循环的时候，在剩余子信道中至少有一个子信道（对应于噪声功率最大的子信道）的功率为0，直到获得最优的 1 ν ∗ \frac{1}{\nu^*} ν∗1​ 与 p n ∗ > 0 p_n^*>0 pn∗​>0 为止。上述方法获得的解称作集中式解，记作向量 p ∗ p^* p∗ 。这个解也是 λ 1 = ⋯ = λ N \lambda_1=\dots=\lambda_N λ1​=⋯=λN​ 时， ( ∗ ) (*) (∗) 式的最优解；也是凸矢量优化问题式 ( ∗ ) (*) (∗) 的 Pareto 最优解，其在 Pareto 边界上的目标函数值为：

( R 1 ∗ = l o g ( 1 + p 1 ∗ σ 1 2 , … , R n ∗ = l o g ( 1 + p N ∗ σ N 2 ) ) (R_1^*=log(1+\frac{p_1^*}{\sigma_1^2},\dots,R_n^*=log(1+\frac{p_N^*}{\sigma_N^2})) (R1∗​=log(1+σ12​p1∗​​,…,Rn∗​=log(1+σN2​pN∗​​))

上述思想的核心原理如下图所示：

三、问题2的研究现状（文献综述）

现状 1 ：

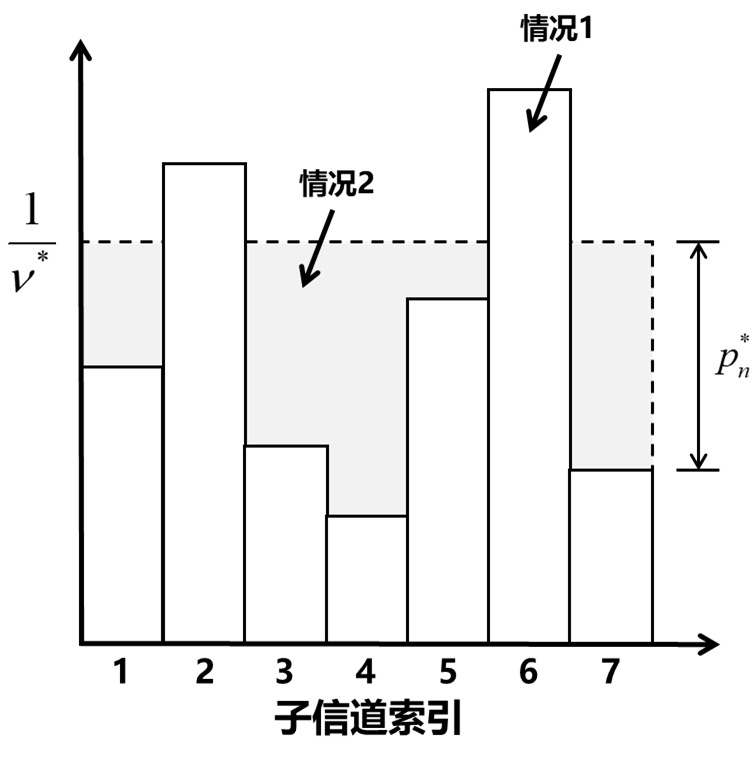
Iterative waterfilling (迭代注水，后文简称 IWF) [2] 是早期的多用户频谱优化技术之一，它利用DSL调制解调器进行频谱整形。在IWF算法中，每个用户通过执行单用户注水，将来自所有其他用户的串扰干扰视为噪声，迭代地最大化自己的可实现速率。但是，IWF进程并不寻求为整个DSL包找到全局最优。该方法只是将每个用户都看成一个非合作博弈的参与者，最终IWF会收敛至一个均衡点。虽然IWF不是最优的，但该方法已被证明优于传统的SSM方案。
解释：
这里以OFDM为例，解释一下上述加粗字体的含义。首先，信道容量可计算为： C = l o g ( 1 + P N ) C=log(1+\frac{P}{N}) C=log(1+NP​)，其中 P P P 是信号功率， N N N 是噪声功率。如果总信号功率被拆为两部分，即： P = P 1 + P 2 P=P_1+P_2 P=P1​+P2​，则可以验证以下公式：

C = l o g ( 1 + P 1 + P 2 N ) = l o g ( ( 1 + P 1 N ) + P 2 N ) = l o g [ ( 1 + P 1 N ) ( 1 + P 2 P 1 + N ) ] = l o g ( 1 + P 1 N ) + l o g ( 1 + P 2 P 1 + N ) \begin{align} C&=log(1+\frac{P_1+P_2}{N})=log((1+\frac{P_1}{N})+\frac{P_2}{N}) \nonumber \\ &=log\left[(1+\frac{P_1}{N})(1+\frac{P_2}{P_1+N})\right] \nonumber \\ &=log(1+\frac{P_1}{N}) +log(1+\frac{P_2}{P_1+N}) \nonumber \end{align} C​=log(1+NP1​+P2​​)=log((1+NP1​​)+NP2​​)=log[(1+NP1​​)(1+P1​+NP2​​)]=log(1+NP1​​)+log(1+P1​+NP2​​)​
也就是说，在这两部分功率中，第一份功率 P 1 P_1 P1​ 产生了一个容量 l o g ( 1 + P 1 N ) log(1+\frac{P_1}{N}) log(1+NP1​​) ，功率 P 1 P_1 P1​ 同时等效成了对第二份功率的噪声。了解了这个原理，不难读懂 IWF 算法中，“每个用户通过执行单用户注水，将来自所有其他用户的串扰干扰视为噪声，迭代地最大化自己的可实现速率”的原理及算法思想了。

现状 2 ：

[3]提出精确OSB算法，可实现全局最优解，该方法的基本策略是将信道容量优化问题 P 2 P_2 P2​ 转化为对偶域，转换成拉格朗日对偶的形式：

P 3 : min ⁡ p ∑ k = 1 K w k ∑ n = 1 N l o g ( 1 + p k n σ k n + ∑ j ≠ k α j k n p j n ) + ∑ k = 1 K λ k ( P k − ∑ n = 1 N p n ) s . t . p k n ≥ 0 ,    ∀ k \begin{align} {P_3:}&\mathop{\min}_{p}{ \sum\limits_{k=1}^K w_k \sum\limits_{n=1}^N log(1+\frac{p^n_k}{\sigma_k^n+\sum_{j \neq k}\alpha_{jk}^n p_j^n)} + \sum\limits_{k=1}^K \lambda_k (P_k - \sum\limits_{n=1}^{N}p_n) } \nonumber \\ &s.t. p_k^n \geq 0, \ \ \forall k \nonumber \end{align} P3​:​minp​k=1∑K​wk​n=1∑N​log(1+σkn​+∑j=k​αjkn​pjn​)pkn​​+k=1∑K​λk​(Pk​−n=1∑N​pn​)s.t.pkn​≥0,  ∀k​

该文献的核心思想是为每个非负且固定的 ( λ 1 , λ 2 , … , λ K ) (\lambda_1,\lambda_2,\dots,\lambda_K) (λ1​,λ2​,…,λK​) 集合，分别求解其拉格朗日函数。然后，原优化问题 P 2 P_2 P2​ 的解，可在 λ \lambda λ 空间内，通过嵌套式的二分法搜索找到。可以看出，OSB算法的计算复杂度与载波数 N N N 呈线性关系。如[3]所示，与IWF相比，OSB算法可以提供显著的性能改进。
OSB算法的缺点：OSB算法的计算复杂度虽然对载波数 N N N 是线性的，但在用户数量 K K K 上仍然是指数级的。即：OSB算法的复杂性变得令人望而却步。

四、问题2的求解方法（优化理论）

在本节我将先后介绍时域共享条件（Time-Sharing Condition）及其证明[4]，随后说明有干扰场景下的信道容量最大化问题 P 2 P_2 P2​ 满足 Time-Sharing Condition。

PART I ： Time-Sharing Condition

在多载波系统中，优化目标和约束通常由大量单独的函数组成，每个函数对应于一个频率载波。因此，优化问题具有以下一般形式：【记下式为 ( ∗ ∗ ) (**) (∗∗) 式】
P 4 : max ⁡ p ∑ n = 1 N f n ( x n ) s . t .   ∑ n = 1 N h n ( x n ) ≤ P \begin{align} {P_4:}&\mathop{\max}_{p}{ \sum\limits_{n=1}^N f_n(x_n) } \nonumber \\ &s.t. \ \sum\limits_{n=1}^N h_n(x_n)\leq P \nonumber \end{align} P4​:​maxp​n=1∑N​fn​(xn​)s.t. n=1∑N​hn​(xn​)≤P​
其中， x n ∈ R K x_n \in \mathcal{R}^K xn​∈RK 为优化问题中的决策变量，函数 f n ( x ) : R K → R f_n(x):\mathcal{R}^K \rightarrow \mathcal{R} fn​(x):RK→R 不必是凹函数，函数 h n ( x ) : R K → R K h_n(x):\mathcal{R}^K \rightarrow \mathcal{R}^K hn​(x):RK→RK 也不必是凸函数。功率约束以 K K K 维向量 P P P 表示，即：component-wise inequality。

上述的泛化优化问题， 在考虑 N N N 个子载波、 K K K 个用户的场景下，对应在多用户 OFDM 系统中有下述结论：

{ x n = ( p 1 n , p 2 n , … , p K n ) ∈ R K f n ( x n ) = ∑ k = 1 K w k l o g ( 1 + p k n σ k n + ∑ j ≠ k α j k n p j n ) h n ( x n ) = [ p 1 n , p 2 n , … , p K n ] T \begin{align} \begin{cases} x_n = (p_1^n,p_2^n,\dots,p_K^n) \in \mathcal{R}^K \nonumber \\ f_n(x_n)={ \sum_{k=1}^K w_k log(1+\frac{p^n_k}{\sigma_k^n+\sum_{j \neq k}\alpha_{jk}^n p_j^n }) } \nonumber \\ h_n(x_n)= \left[ p_1^n, p_2^n, \dots, p_K^n \right]^T \end{cases} \end{align} ⎩ ⎨ ⎧​xn​=(p1n​,p2n​,…,pKn​)∈RKfn​(xn​)=∑k=1K​wk​log(1+σkn​+∑j=k​αjkn​pjn​pkn​​)hn​(xn​)=[p1n​,p2n​,…,pKn​]T​​

下面考虑 ( ∗ ∗ ) (**) (∗∗) 式的对偶问题，先求其 Lagrangian 函数：

L ( x n , λ ) = ∑ n = 1 N f n ( x n ) + λ T ( P − ∑ n = 1 N h n ( x n ) ) L(x_n,\lambda)=\sum\limits_{n=1}^{N}f_n(x_n) +\lambda^T(P-\sum\limits_{n=1}^{N}h_n(x_n)) L(xn​,λ)=n=1∑N​fn​(xn​)+λT(P−n=1∑N​hn​(xn​))

定义对偶目标函数 g ( λ ) g(\lambda) g(λ) 如下：

g ( λ ) = max ⁡ L ( x n , λ ) g(\lambda)=\max {L(x_n,\lambda)} g(λ)=maxL(xn​,λ)

则对偶优化问题为：
P 5 : min ⁡ λ g ( λ ) s . t . λ ≥ 0 \begin{align} {P_5:}&\mathop{\min}_{\lambda}{ g(\lambda) } \nonumber \\ &s.t. \lambda \geq 0 \nonumber \end{align} P5​:​minλ​g(λ)s.t.λ≥0​

显然，当 f n ( x n ) f_n(x_n) fn​(xn​) 是凹函数且 h n ( x n ) h_n(x_n) hn​(xn​) 是凸函数时，标准凸优化结果保证了原问题 P 4 P_4 P4​ 与对偶问题 P 5 P_5 P5​ 具有相同的解，此时对偶间隙为0。而当 f n ( x n ) f_n(x_n) fn​(xn​) 不是凹函数或 h n ( x n ) h_n(x_n) hn​(xn​) 不是凸函数时，对偶问题提供了一个解，该解是 P 5 P_5 P5​ 的上界，此时对偶间隙未必是0。这是教材告诉我们的。**而本节的主要目的，是给出即使优化问题不是凸问题，对偶间隙也为零的条件。**为此，定义了以下 Time-Sharing Condition：

定义：
令 x n ∗ x_n^* xn∗​ 与 y n ∗ y_n^* yn∗​ 分别是在给定 P = P x P=P_x P=Px​ 与给定 P = P y P=P_y P=Py​ 条件下，优化问题 P 4 P_4 P4​ 的最优解。如果对任意的 P x P_x Px​ 与 P y P_y Py​ ，对任意的 0 ≤ ν ≤ 1 0 \leq \nu\leq1 0≤ν≤1 ，都存在一个可行的 z n z_n zn​ ，使得下式成立：
{ ∑ n = 1 N h n ( z n ) ≤ ν P x + ( 1 − ν ) P y ∑ n = 1 N f n ( z n ) ≥ ν ∑ n = 1 N f n ( x n ∗ ) + ( 1 − ν ) ∑ n = 1 N f n ( y n ∗ ) \begin{align} \begin{cases} \sum\limits_{n=1}^{N}h_n(z_n)\leq \nu P_x + (1-\nu) P_y \nonumber \\ \sum\limits_{n=1}^{N}f_n(z_n)\geq \nu \sum\limits_{n=1}^{N}f_n(x_n^*) + (1-\nu)\sum\limits_{n=1}^{N} f_n(y_n^*) \nonumber \end{cases} \end{align} ⎩ ⎨ ⎧​n=1∑N​hn​(zn​)≤νPx​+(1−ν)Py​n=1∑N​fn​(zn​)≥νn=1∑N​fn​(xn∗​)+(1−ν)n=1∑N​fn​(yn∗​)​​
则称优化问题 P 4 P_4 P4​ 满足 Time-Sharing Condition。

理解：
上述定义看起来很玄幻，但其本质并不难理解。首先，要知道原始优化问题 的最优解（optimal solutions）是 x n ∗ x_n^* xn∗​，很显然 x n ∗ x_n^* xn∗​ 必须满足约束 ∑ n = 1 N h n ( x n ∗ ) = P \sum\limits_{n=1}^N h_n(x_n^*) = P n=1∑N​hn​(xn∗​)=P 为紧约束。因此，约束上限 P P P 的取值，决定了 x n ∗ x_n^* xn∗​ 的取值。所以，我们也可以将 x n ∗ x_n^* xn∗​ 看成 P P P 的函数，即： x n ∗ = x n ∗ ( P ) x_n^*=x_n^*(P) xn∗​=xn∗​(P) 。其次，理解了这一点，就可以理解为什么定义中要给定 P = P x P=P_x P=Px​ 与 P = P y P=P_y P=Py​ 这两种情况了，其实就是为了刻画 x n ∗ = x n ∗ ( P x ) x_n^*=x_n^*(P_x) xn∗​=xn∗​(Px​) 以及 y n ∗ = y n ∗ ( P y ) y_n^*=y_n^*(P_y) yn∗​=yn∗​(Py​) ，通过变化不同的 P P P 值（体现在定义中“对任意的 P = P x P=P_x P=Px​ 与 P = P y P=P_y P=Py​ ”一句），研究函数的性质。最后，需要理解作者为什么要这么刻画呢？其实就是为了说明函数整体的凹凸性而已。观察第一条约束描述的是对整体约束函数 ∑ n = 1 N h n ( x n ) \sum\limits_{n=1}^N h_n(x_n) n=1∑N​hn​(xn​) 凸性的刻画（注意，刻画的不是单独的 h n ( x n ) h_n(x_n) hn​(xn​) 函数，没必要研究单独的一个 h n ( x n ) h_n(x_n) hn​(xn​) 函数是否为凸性）；观察第二条约束描述的是整体目标函数 ∑ n = 1 N f n ( x n ) \sum\limits_{n=1}^N f_n(x_n) n=1∑N​fn​(xn​) 凹性的刻画。

因此，可以理解 Time-Sharing Condition 无非是通过刻画求和后，函数整体的凹凸性，以替代单独每一个函数凹凸性。显然，如果每一个函数的凹凸性得到满足，那么 Time-Sharing Condition 自然成立，因此这部分理论也被称为广义对偶理论（General Duality Theory）。

PART II ： 定理及其证明

接下来介绍 Time-Sharing Condition 有什么作用？主要体现在下述定理：

定理：
考虑如 所示的优化问题形式，如果满足 Time-Sharing Condition，则该优化问题的对偶间隙为0。

证明：

显然，如果 h n ( x n ) h_n(x_n) hn​(xn​) 是凸函数、 f n ( x n ) f_n(x_n) fn​(xn​) 是凹函数，根据保凸运算易知，优化问题是凸优化问题，则其对偶间隙为0。下面我们证明：当 h n ( x n ) h_n(x_n) hn​(xn​) 不是凸函数、 f n ( x n ) f_n(x_n) fn​(xn​) 不是凹函数，但优化问题 P 4 P_4 P4​ 满足 Time-Sharing Condition 时，其对偶间隙仍为0。

令向量 P x , P y P_x, P_y Px​,Py​ 和 P z P_z Pz​ 是满足 P z = ν P x + ( 1 − ν ) P y P_z=\nu P_x + (1-\nu)P_y Pz​=νPx​+(1−ν)Py​ 的功率约束向量（注意：这里的向量 ν \nu ν 是只要找到或存在一个属于 [ 0 , 1 ] [0,1] [0,1] 区间的 ν \nu ν ，使得上述等式成立即可），令 x n ∗ , y n ∗ x_n^*,y_n^* xn∗​,yn∗​ 和 z n ∗ z_n^* zn∗​ 是在 P x , P y P_x, P_y Px​,Py​ 和 P z P_z Pz​ 功率约束下优化问题 P 4 P_4 P4​ 的最优解（注意：这里的逻辑是先给出一组满足上述等式的功率约束组 { P x , P y , P z } \{P_x, P_y, P_z\} {Px​,Py​,Pz​} ，然后依据这三个数，分别求出他们对应的最优解 { x n ∗ , y n ∗ , z n ∗ } \{x_n^*,y_n^*,z_n^*\} {xn∗​,yn∗​,zn∗​} ）。

第一步证明：基于 Time-Sharing Condition ，证明 是关于 的凹函数

这里我先给出适当说明，然后再讲述原文步骤，不然直接看原文容易懵逼：
Step（a）先将 ∑ n f n ( x n ∗ ) \sum_{n}f_n(x_n^*) ∑n​fn​(xn∗​) 写为 ∑ n f n ( x n ∗ ( P x ) ) \sum_{n}f_n(x_n^*(P_x)) ∑n​fn​(xn∗​(Px​)) 的形式；
Step（b）为简洁表示，记 g ( P x ) = ∑ n f n ( x n ∗ ( P x ) ) g(P_x)=\sum_{n}f_n(x_n^*(P_x)) g(Px​)=∑n​fn​(xn∗​(Px​)) ;
Step（c）因此，我们需要证明：对任意的 P x , P y P_x,P_y Px​,Py​ ，对任意的 ν ∈ [ 0 , 1 ] \nu\in \left[0,1\right] ν∈[0,1]，都有 g ( ν P x + ( 1 − ν ) P y ) ≥ ν g ( P x ) + ( 1 − ν ) g ( P y ) g(\nu P_x+(1-\nu)P_y) \geq \nu g(P_x)+(1-\nu)g(P_y) g(νPx​+(1−ν)Py​)≥νg(Px​)+(1−ν)g(Py​) 成立；
Step（d）也就是需要证明下式成立
∑ n f n ( x n ∗ ( ν P x + ( 1 − ν ) P y ) ) ≥ ν ∑ n f n ( x n ∗ ( P x ) ) + ( 1 − ν ) ∑ n f n ( y n ∗ ( P y ) ) \begin{align} \sum_{n}f_n(x_n^*(\nu P_x+(1-\nu & )P_y)) \nonumber \\ \geq \nu &\sum_{n}f_n(x_n^*(P_x))+(1-\nu)\sum_{n}f_n(y_n^*(P_y)) \nonumber \end{align} n∑​fn​(xn∗​(νPx​+(1−ν≥ν​)Py​))n∑​fn​(xn∗​(Px​))+(1−ν)n∑​fn​(yn∗​(Py​))​
注意：左式 x n ∗ ( ν P x + ( 1 − ν ) P y ) x_n^*(\nu P_x+(1-\nu )P_y) xn∗​(νPx​+(1−ν)Py​) 中的 x n ∗ x_n^* xn∗​ 写法不严谨，需要依据内部的自变量而定。在这里，严谨的应该写为 q ( x n ∗ y n ∗ ) ( ν P x + ( 1 − ν ) P y ) q(x_n^*y_n^*)(\nu P_x+(1-\nu )P_y) q(xn∗​yn∗​)(νPx​+(1−ν)Py​) ， 表示是 P x P_x Px​ 与 P y P_y Py​ 的函数多对应的 x n ∗ x_n^* xn∗​ 与 y n ∗ y_n^* yn∗​ 的函数。
Step（e）因为 P z = ν P x + ( 1 − ν ) P y P_z=\nu P_x + (1-\nu)P_y Pz​=νPx​+(1−ν)Py​ ，所以需要证明下式成立即可：
∑ n f n ( z n ∗ ( P z ) ) ≥ ν ∑ n f n ( x n ∗ ( P x ) ) + ( 1 − ν ) ∑ n f n ( y n ∗ ( P y ) ) \begin{align} \sum_{n}f_n(z_n^*(P_z )) \geq \nu &\sum_{n}f_n(x_n^*(P_x))+(1-\nu)\sum_{n}f_n(y_n^*(P_y)) \nonumber \end{align} n∑​fn​(zn∗​(Pz​))≥ν​n∑​fn​(xn∗​(Px​))+(1−ν)n∑​fn​(yn∗​(Py​))​
注意：左式直接替换上述等式后，应为 f n ( x n ∗ ( P z ) ) f_n(x_n^*(P_z )) fn​(xn∗​(Pz​))，但此时自变量是 P z P_z Pz​ 了，因此对应改为 f n ( z n ∗ ( P z ) ) f_n(z_n^*(P_z )) fn​(zn∗​(Pz​)) 。

看完前面的解释，再看原文证明步骤，简述如下：
Step（1）因为 Time-Sharing Condition 成立，所以对前文给定的 P x , P y P_x, P_y Px​,Py​ 以及给定的 ν \nu ν，一定存在一个 z ~ \widetilde{z} z ，使得下式成立：
{ ∑ n = 1 N h n ( z ~ n ) ≤ ν P x + ( 1 − ν ) P y ∑ n = 1 N f n ( z ~ n ) ≥ ν ∑ n = 1 N f n ( x n ∗ ) + ( 1 − ν ) ∑ n = 1 N f n ( y n ∗ ) \begin{align} \begin{cases} \sum\limits_{n=1}^{N}h_n(\widetilde{z}_n)\leq \nu P_x + (1-\nu) P_y \nonumber \\ \sum\limits_{n=1}^{N}f_n(\widetilde{z}_n)\geq \nu \sum\limits_{n=1}^{N}f_n(x_n^*) + (1-\nu)\sum\limits_{n=1}^{N} f_n(y_n^*) \nonumber \end{cases} \end{align} ⎩ ⎨ ⎧​n=1∑N​hn​(z n​)≤νPx​+(1−ν)Py​n=1∑N​fn​(z n​)≥νn=1∑N​fn​(xn∗​)+(1−ν)n=1∑N​fn​(yn∗​)​​
注意：这里的 z ~ \widetilde{z} z 与前文的 z z z 不一样，但原文中并没有声明，我在推送里区分一下，故用 z ~ \widetilde{z} z 表示。
Step（2）又因为 z ~ \widetilde{z} z 是优化问题可行集内的一个可行点，这意味着该点对应的目标函数一定小于最优解，因此有下式成立：
∑ n = 1 N f n ( z n ∗ ) ≥ ∑ n = 1 N f n ( z ~ n ) ≥ ν ∑ n = 1 N f n ( x n ∗ ) + ( 1 − ν ) ∑ n = 1 N f n ( y n ∗ ) \begin{align} \sum\limits_{n=1}^{N}f_n(z_n^*)\geq\sum\limits_{n=1}^{N}f_n(\widetilde{z}_n)\geq \nu \sum\limits_{n=1}^{N}f_n(x_n^*) + (1-\nu)\sum\limits_{n=1}^{N} f_n(y_n^*) \nonumber \end{align} n=1∑N​fn​(zn∗​)≥n=1∑N​fn​(z n​)≥νn=1∑N​fn​(xn∗​)+(1−ν)n=1∑N​fn​(yn∗​)​
Step（3）根据Step(a)-Step(e)的解释可知，上式便是Step(e)中的结论，所以， ∑ n f n ( x n ∗ ) \sum_{n}f_n(x_n^*) ∑n​fn​(xn∗​) 是关于 P P P 的凹函数得证。

注意：原文没有Step(a)-Step(e)的解释，我看到论文中Step(2)后，最开始不太明白，为什么Step(2)成立后， ∑ n f n ( x n ∗ ) \sum_{n}f_n(x_n^*) ∑n​fn​(xn∗​) 就是关于 P P P 的凹函数了？后来才想明白的，所以记录在Step(a)-Step(e)的解释里。

第二步证明：利用 ∑ n f n ( x n ∗ ) \sum_{n}f_n(x_n^*) ∑n​fn​(xn∗​) 是关于 P P P 的凹函数的性质，证明对偶间隙为0

Step（1）考虑到 ∑ n f n ( x n ∗ ) \sum_{n}f_n(x_n^*) ∑n​fn​(xn∗​) 是关于 P P P 的凹函数，所以我们以 P P P 为横坐标（等价于以 ∑ n h n ( x n ∗ ) \sum_{n}h_n(x_n^*) ∑n​hn​(xn∗​)为横坐标，因为 ∑ n h n ( x n ∗ ) = P \sum_{n}h_n(x_n^*)=P ∑n​hn​(xn∗​)=P 显然成立），以 ∑ n f n ( x n ∗ ) \sum_{n}f_n(x_n^*) ∑n​fn​(xn∗​) 为纵坐标，用实线画出如下图所示凹函数：

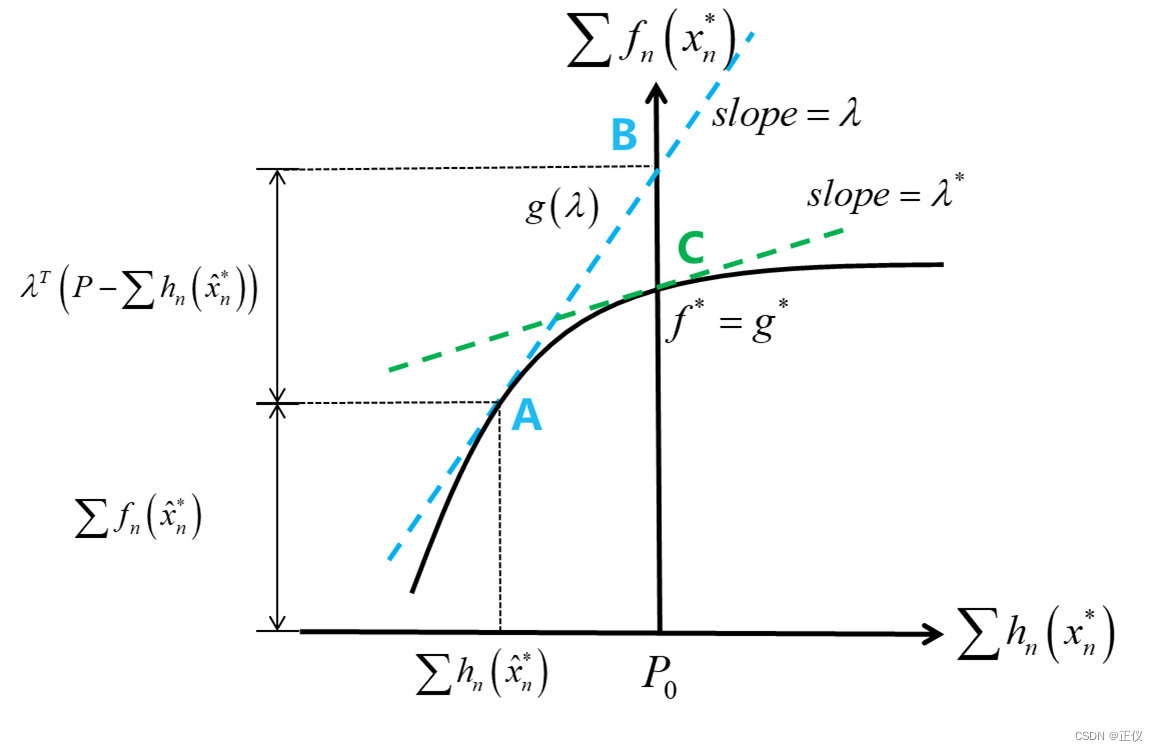
理解：
显然，在变化 P P P 的时候（即变化 ∑ n h n ( x n ∗ ) \sum_{n}h_n(x_n^*) ∑n​hn​(xn∗​) 的时候）， x n ∗ x_n^* xn∗​ 也随之而变，导致目标函数 ∑ n f n ( x n ∗ ) \sum_{n}f_n(x_n^*) ∑n​fn​(xn∗​) 也随之而变，所以，可以画出 ∑ n h n ( x n ∗ ) \sum_{n}h_n(x_n^*) ∑n​hn​(xn∗​)与 ∑ n f n ( x n ∗ ) \sum_{n}f_n(x_n^*) ∑n​fn​(xn∗​) 之间的变化规律图（即函数图）。而前文证明了，这个函数是凹函数，因此可以做出曲线 ( ∑ n h n ( x n ∗ ) , ∑ n f n ( x n ∗ ) ) (\sum_{n}h_n({x}_n^*),\sum_{n}f_n({x}_n^*)) (∑n​hn​(xn∗​),∑n​fn​(xn∗​)) 如图实线所示。

Step（2）又考虑到 g ( λ ) g(\lambda) g(λ) 可写成下式：
g ( λ ) = max ⁡ x n ( ∑ n f n ( x n ) + λ T ( P − ∑ n h n ( x n ) ) ) \begin{align} g(\lambda)&=\mathop{\max}_{x_n}\left( \sum_{n}f_n(x_n)+\lambda^T \left( P-\sum_{n}h_n(x_n) \right) \right) \nonumber \end{align} g(λ)​=maxxn​​(n∑​fn​(xn​)+λT(P−n∑​hn​(xn​)))​

令 x ^ n ∗ \hat{x}_n^* x^n∗​ 是上述优化问题的最优解，则 g ( λ ) g(\lambda) g(λ) 可写为下式：

g ( λ ) = ∑ n f n ( x ^ n ∗ ) + λ T ( P − ∑ n h n ( x ^ n ∗ ) ) g(\lambda)=\sum_{n}f_n(\hat{x}_n^*)+\lambda^T \left( P-\sum_{n}h_n(\hat{x}_n^*) \right) g(λ)=n∑​fn​(x^n∗​)+λT(P−n∑​hn​(x^n∗​))

显然， g ( λ ) g(\lambda) g(λ) 是关于 P P P 的线性函数，且斜率为 λ \lambda λ 。因此，根据其几何意义，我们可在曲线 ( ∑ n h n ( x n ∗ ) , ∑ n f n ( x n ∗ ) ) (\sum_{n}h_n({x}_n^*),\sum_{n}f_n({x}_n^*)) (∑n​hn​(xn∗​),∑n​fn​(xn∗​)) 上，做一条切线，且切点为 ( ∑ n h n ( x ^ n ∗ ) , ∑ n f n ( x ^ n ∗ ) ) (\sum_{n}h_n(\hat{x}_n^*),\sum_{n}f_n(\hat{x}_n^*)) (∑n​hn​(x^n∗​),∑n​fn​(x^n∗​)) 。此外，这条切线与纵坐标的交点为 ∑ n f n ( x ^ n ∗ ) + λ T ( P − ∑ n h n ( x ^ n ∗ ) ) \sum_{n}f_n(\hat{x}_n^*)+\lambda^T \left( P-\sum_{n}h_n(\hat{x}_n^*) \right) ∑n​fn​(x^n∗​)+λT(P−∑n​hn​(x^n∗​)) ，而这个交点，便是 g ( λ ) g(\lambda) g(λ) 的确切取值（即图中的点 B B B ）。

Step（3）对偶问题中，需要通过寻找 λ \lambda λ，以最小化 g ( λ ) g(\lambda) g(λ) ，记最优解为 g ∗ g^* g∗ 。显然，只有当曲线 ( ∑ n h n ( x n ∗ ) , ∑ n f n ( x n ∗ ) ) (\sum_{n}h_n({x}_n^*),\sum_{n}f_n({x}_n^*)) (∑n​hn​(xn∗​),∑n​fn​(xn∗​)) 是凹的，此时在整条曲线上寻找最优的切线斜率 λ \lambda λ 时，才可以找到最优的 λ ∗ \lambda^* λ∗ 。此时， g ( λ ) g(\lambda) g(λ) 与纵坐标交点的最小值就等于曲线自身的最小值，即：f^*=g* ，如图中点 C C C 所示。

Step（4）为了说明 Time-Sharing Condition 的重要性，下图说明了当该条件不成立的时候，对偶间隙不为0。

PART III ：用Time-Sharing Condition解释问题2

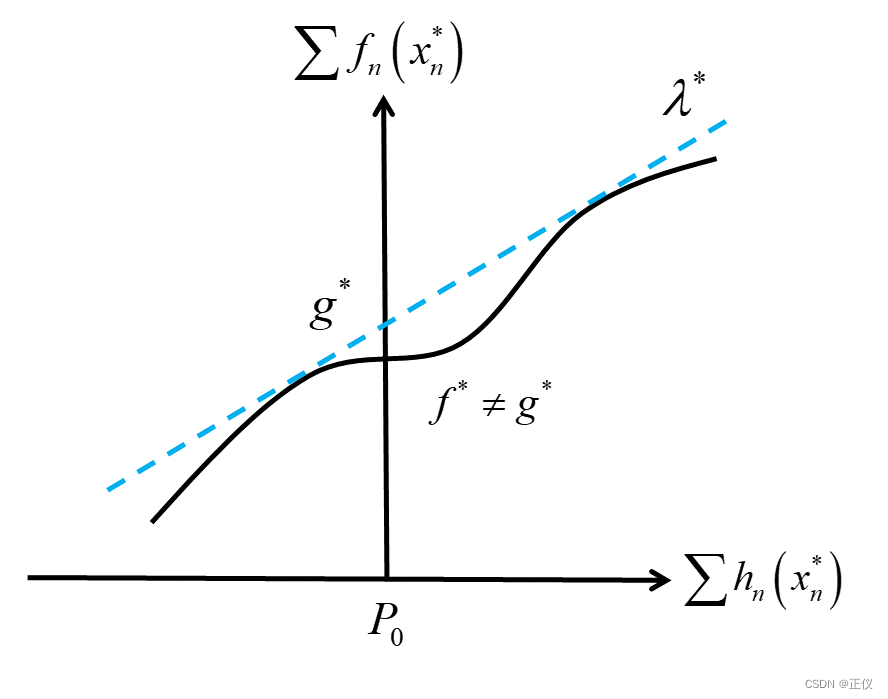
方案1： 如果OFDM系统可以实现完美的时分复用功能，则 Time-Sharing Condition 显然满足，直观解释如下：
令 x n x_n xn​ 与 y n y_n yn​ 是两种功率分配方案。在这种情况下，全部的频谱带宽可以以 ν \nu ν 的比率分配给策略 x n x_n xn​ ，以 1 − ν 1-\nu 1−ν 的比例分给策略 y n y_n yn​ 。此时，原始的目标函数变为两套方案的线性组合，即：
∑ n f n = ∑ n [ ν f n ( x n ) + ( 1 − ν ) f n ( y n ) ] \sum_{n} f_n= \sum_{n}\left[\nu f_n(x_n)+(1-\nu) f_n(y_n)\right] n∑​fn​=n∑​[νfn​(xn​)+(1−ν)fn​(yn​)]
与此同时，约束也是时隙分配的线性组合，此时为线性关系，自然满足 Time-Sharing Condition中的凹性与凸性 。

方案2： 如果OFDM系统可以实现频分复用功能，且子载波数 N → + inf ⁡ N \rightarrow +\inf N→+inf ，此时，通过在频域上按比例 ν \nu ν 交错 x n x_n xn​ 与 y n y_n yn​ ，则也可以得到上述结论。

参考文献：

[1]祁忠勇.信号处理与通信中的凸优化: 从基础到应用,2019:300-302.
[2]Yu W, Ginis G, Cioffi J M. Distributed multiuser power control for digital subscriber lines[J]. IEEE Journal on Selected areas in Communications, 2002, 20(5): 1105-1115.
[3]Cendrillon R, Yu W, Moonen M, et al. Optimal multiuser spectrum balancing for digital subscriber lines[J]. IEEE Transactions on Communications, 2006, 54(5): 922-933.
[4]Yu W, Lui R. Dual methods for nonconvex spectrum optimization of multicarrier systems[J]. IEEE Transactions on communications, 2006, 54(7): 1310-1322.

文字 | 正仪
编辑 | 正仪
作图 | 正仪

更多优化内容，欢迎关注本人微信公众号：优化与博弈的数学原理

最后，助大家学业有成！早日毕业~