虽然基于CCA的方法在识别SSVEP信号方面具有不错的表现,但这类方法的性能仍旧易受到自发脑电活动的干扰的影响。除此之外,研究人员们考虑到基于CCA的方法还有一个很大的问题,即没有利用到相位信息(参考信号中正余弦中没有包含相位项)。那么如果能够有效地利用相位信息,想必会给SSVEP的识别性能带来较大的提升。
由此研究人员便提出了TRCA方法,TRCA的方法即通过最大化每个task中神经影像数据的复现性(reproducibility),提取任务相关成分(task-related com-ponents)。对于SSVEP这种锁时(time-locked)信号,该方法非常合适,因为在SSVEP中可以最大化多个trial之间的可再现性,提高SNR(Signal-to-Noise),抑制自发脑电活动。
a)、首先,我们认为待识别的SSVEP信号
X
(
t
)
X(t)
X(t)通常由任务相关(task-related)信号
s
(
t
)
s(t)
s(t)和任务无关(task-independent)信号
n
(
t
)
n(t)
n(t)组成,即
x
j
(
t
)
=
a
1
,
j
s
(
t
)
+
a
2
,
j
n
(
t
)
,
j
=
1
,
2
,
…
N
c
x_j (t)=a_{1,j} s(t)+a_{2,j} n(t),j=1,2,…N_c
xj(t)=a1,js(t)+a2,jn(t),j=1,2,…Nc
其中,
a
1
,
j
a_{1,j}
a1,j 、
a
2
,
j
a_{2,j}
a2,j表示混合系数。除此之外,
s
(
t
)
s(t)
s(t)在跨试次过程中保持着不变性,而
n
(
t
)
n(t)
n(t)在跨试次中是变化的,导致它们两者间存在着这么一个性质:对于某一个时间窗口内的
s
(
i
)
和
n
(
i
)
s^{(i)} 和n^{(i)}
s(i)和n(i),
s
(
i
)
s^{(i)}
s(i) 之间的协方差为一个正常数,而
s
(
i
)
s^{(i)}
s(i)和
n
(
i
)
n^{(i)}
n(i)之间的协方差为0。
b)、我们期望能从
X
(
t
)
X(t)
X(t)中提取到任务相关成分
s
(
t
)
s(t)
s(t),为此我们首先对多通道的EEG信号进行加权求和。
y
(
t
)
=
∑
j
=
1
N
c
w
j
∗
x
j
(
t
)
=
∑
j
=
1
N
c
(
w
j
∗
a
1
,
j
s
(
t
)
+
w
j
∗
a
2
,
j
n
(
t
)
)
y(t)=\sum_{j=1}^{N_c}w_j*x_j(t)=\sum_{j=1}^{N_c}(w_j*a_{1,j} s(t)+w_j*a_{2,j} n(t))
y(t)=j=1∑Ncwj∗xj(t)=j=1∑Nc(wj∗a1,js(t)+wj∗a2,jn(t))
为了达到我们期待的目标,使得任务相关成分
y
(
t
)
=
s
(
t
)
y(t)=s(t)
y(t)=s(t)那么就必须有
∑
j
=
1
N
c
w
j
∗
a
1
,
j
=
1
,
∑
j
=
1
N
c
w
j
∗
a
2
,
j
=
0
\sum_{j=1}^{N_c}w_j*a_{1,j}=1,\quad \sum_{j=1}^{N_c}w_j*a_{2,j}=0
j=1∑Ncwj∗a1,j=1,j=1∑Ncwj∗a2,j=0
如果我们得到了这样的一个解,那么多通道的EEG信号经过线性加权求和后,便能够得到在多个trial之间的高相关性的 y ( t ) y(t) y(t)。
c)、那么接下来的问题就是去求解上述方程解的中的 w w w。其中一种方案是采用基于皮尔森相关系数的Correlation Maximization(CorrMax)，但该方法的解并不是封闭解(封闭解即解析解,可根据可表达的函数形式对任意所给的自变量求出对应的因变量),而且只能得到一个任务相关成分。故实际上在SSVEP识别任务中,采用的是另外一种方法——基于协方差的Covariance Maximiza-tion(CovMax)。
d)、记 h 1 t h h_1^{th} h1th trial的EEG信号与任务相关成分为 x ( h 1 ) ( t ) x^{(h1)} (t) x(h1)(t)和 y ( h 1 ) ( t ) y^{(h1)}(t) y(h1)(t), 记 h 2 t h − t r i a l h2^{th} -trial h2th−trial的EEG信号与任务相关成分为 x ( h 2 ) ( t ) x^{(h2)}(t) x(h2)(t)和 y ( h 2 ) ( t ) y^{(h2)}(t) y(h2)(t),那么 h 1 t h h_1^{th} h1th trial和 h 2 t h h_2^{th} h2th trial的 y ( t ) y(t) y(t)之间的协方差可由下式表示:
C h 1 , h 2 = C o v ( y ( h 1 ) ( t ) , y ( h 2 ) ( t ) ) \quad \quad \quad \quad C_{h1,h2}=Cov(y^{(h1)} (t),y^{(h2)}(t)) Ch1,h2=Cov(y(h1)(t),y(h2)(t))
= ∑ j 1 , j 2 = 1 N c w j 1 w j 2 C o v ( x j 1 ( h 1 ) ( t ) , x j 2 ( h 2 ) ( t ) ) \quad \quad \quad \quad \quad \quad=\sum_{j_1,j_2=1}^{N_c}w_{j_1}w_{j_2}Cov(x_{j_1}^{{(h_1)}}(t),x_{j_2}^{{(h_2)}}(t)) =∑j1,j2=1Ncwj1wj2Cov(xj1(h1)(t),xj2(h2)(t))
所有试次的组合可由下式表示:
∑
h
1
,
h
2
=
1
h
1
≠
h
2
N
t
C
h
1
,
h
2
=
∑
h
1
,
h
2
=
1
h
1
≠
h
2
N
t
∑
j
1
,
j
2
=
1
N
c
w
j
1
w
j
2
C
o
v
(
x
j
1
h
1
(
t
)
,
x
j
2
h
2
(
t
)
)
=
w
T
S
w
=
1
\begin{aligned} \sum_{\begin{matrix} {h_1,h_2}=1 \\ h_1≠h_2 \end{matrix}}^{N_t}C_{{h_1},{h_2} }\ &=\sum_{\begin{matrix}h_1,h_2=1 \\ h_1≠h_2 \end{matrix}}^{N_t}\sum_{j_1,j_2=1}^{N_c}w_{j_1}w_{j_2}Cov(x_{j_1}^{h_1}(t),x_{j_2}^{h_2}(t)) \\ \\ &=w^TSw=1 \end{aligned}
h1,h2=1h1=h2∑NtCh1,h2 =h1,h2=1h1=h2∑Ntj1,j2=1∑Ncwj1wj2Cov(xj1h1(t),xj2h2(t))=wTSw=1
其中,对称矩阵S可表示为:
S
j
1
,
j
2
=
∑
h
1
,
h
2
=
1
h
1
≠
h
2
N
t
C
o
v
(
x
j
1
(
h
1
)
(
t
)
)
,
x
j
2
(
h
2
)
(
t
)
)
S_{{j_1},{j_2}}=\sum_{\begin{matrix}h_1,h_2=1 \\ h_1≠h_2 \\ \end{matrix}}^{N_t}Cov(x_{j_1}^{(h_1)}(t)), x_{j_2}^{(h_2)}(t))
Sj1,j2=h1,h2=1h1=h2∑NtCov(xj1(h1)(t)),xj2(h2)(t))
为了得到有效解,我们需要对y(t)做归一化约束,即
V
a
r
(
y
(
t
)
)
=
∑
j
1
,
j
2
=
1
N
c
w
j
1
w
j
2
C
o
v
(
x
j
1
(
h
1
)
(
t
)
)
,
x
j
2
(
h
2
)
(
t
)
)
Var(y(t))=\sum_{j_1,j_2=1}^{N_c}w_{j_1}w_{j_2}Cov(x_{j_1}^{(h_1)}(t)), x_{j_2}^{(h_2)}(t))
Var(y(t))=j1,j2=1∑Ncwj1wj2Cov(xj1(h1)(t)),xj2(h2)(t))
最终,我们的约束优化问题转变为Rayleigh-Ritz特征值问题
w
^
=
argmax
w
w
T
S
w
w
T
Q
w
\hat{w} = {\underset{w}{\operatorname {argmax} }\frac{w^TSw}{w^TQw}}
w^=wargmaxwTQwwTSw
根据Rayleigh-Ritz理论,最佳的系数向量 W W W ̂可通过求解 Q − 1 S Q^{-1} S Q−1S的特征向量得到。 Q − 1 S Q^{-1} S Q−1S的特征向量为一个N维的向量矩阵,每一维对应一个特征值,并且按特征值大小排列。特征值的大小表示了按其对应的特征向量对信号进行空间滤波后, y ( t ) y(t) y(t)在trial之间的任务一致性(task consistency)。而在SSVEP识别过程中,仅使用了最大特征值对应的特征向量。
e)、由于在整个TRCA算法过程中,我们利用了待识别信号 x ( t ) x(t) x(t)去计算得出最佳的 w w w,故表明了TRCA算法也是需要受试者的训练数据的。我们利用受试者某一刺激n的训练数据 X n ( m ) X_n^{(m)} Xn(m)通过TRCA得到对应的空间滤波器 w n ( m ) w_n^{(m) } wn(m),利用 w n ( m ) w_n^{(m)} wn(m)对test trial X ( m ) X^{(m)} X(m)和训练集平均信号 X ‾ n ( m ) \overline X_n^{(m)} Xn(m)进行空间滤波,然后计算两者的Pearson correlation coefficients(皮尔森相关系数)
r n ( m ) = ρ ( ( X ( m ) ) T w n ( m ) , ( ( X n ‾ ) ( m ) ) T w n ( m ) ) r_n^{(m)}=ρ((X^{(m)})^T w_n^{(m)},((\overline{X_n})^{(m)})^T w_n^{(m)} ) rn(m)=ρ((X(m))Twn(m),((Xn)(m))Twn(m))
最后找到最大相关系数对应的刺激频率即可。
理想情况下,SSVEP源信号传递至头表记录的各个电极通道的信号混合系数使用的频率范围是一致的,这导致对于K个刺激类别,TRCA算法学习的K个空间滤波器是具有一定相似度的。Ensemble TRCA算法充分利用这一特性,首先将学习的K个空间滤波器进行结合:
W ( m ) = [ w 1 ( m ) , w 2 ( m ) ⋯ w K ( m ) ] W^{(m)}=[w_{1}^{(m)}, w_{2}^{(m)} \cdots w_{K}^{(m)} ] W(m)=[w1(m),w2(m)⋯wK(m)]
最后使用二维皮尔森相关系数求解识别的刺激频率:
r
n
(
m
)
=
ρ
(
(
X
(
m
)
)
T
W
(
m
)
,
(
(
X
n
‾
)
(
m
)
)
T
W
(
m
)
)
r_n^{(m)}=ρ((X^{(m)})^T W^{(m)},((\overline{X_n})^{(m)})^T W^{(m)} )
rn(m)=ρ((X(m))TW(m),((Xn)(m))TW(m))
TRCA算法和ensemble TRCA的大致流程下图所示。
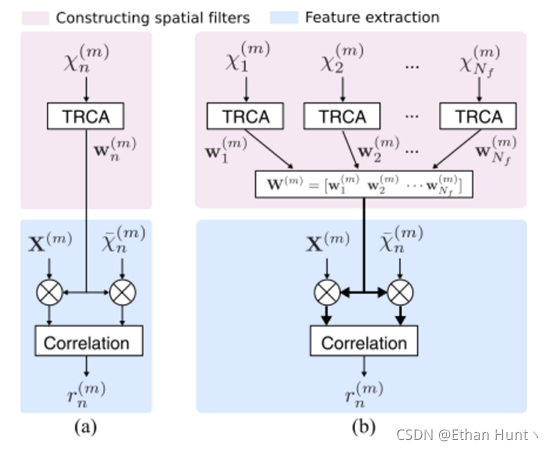
实现代码: https://github.com/YuDongPan/Canonical_Classifier
参考资料与文献:
