目录
一、简介
1.泰勒公式及其证明过程
2.两种类型的余项
3.麦克劳林公式
二、泰勒公式常见题型
1.用泰勒公式展开函数
2.用泰勒公式求极限
3.用泰勒公式讨论无穷小的比较
4.用泰勒公式证明等式和不等式
一、简介
1.泰勒公式及其证明过程
-
泰勒中值定理1:若f(x)在含有
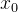 的某个邻域内具有n阶倒数,则对于该邻域内任一点x,(x趋近于
的某个邻域内具有n阶倒数,则对于该邻域内任一点x,(x趋近于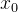 )则有:
)则有:
其中 为余项,根据需要选择使用佩亚诺型还是拉格朗日型,具体见后文(两种类型的余项)
为余项,根据需要选择使用佩亚诺型还是拉格朗日型,具体见后文(两种类型的余项)

 一次表达式
一次表达式
令
当 ;
;
 ,
,  ……
……  先求导再代入
先求导再代入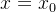
则 ,
,  ……
……  即证。
即证。
2.两种类型的余项
1.佩亚诺型余项 取前一项的自变量
取前一项的自变量
若你所写的泰勒公式只有三项,则 ,取四项则
,取四项则 ,其他同理
,其他同理
2.拉格朗日型余项
泰勒中值定理2: 若f(x)在含有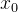 的某个邻域内具有n+1阶导数,则对于该邻域内任一点x,(x趋近于
的某个邻域内具有n+1阶导数,则对于该邻域内任一点x,(x趋近于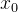 ),则有
),则有 ,此式子即为拉格朗日型余项
,此式子即为拉格朗日型余项
 时
时  即
即  为拉格朗日中值定理
为拉格朗日中值定理
3.麦克劳林公式
当泰勒公式中  时即为麦克劳林公式:
时即为麦克劳林公式: 

注意:麦克劳林公式的使用条件:因为x趋近于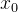 ,而此时
,而此时 ,所以x也趋近于零
,所以x也趋近于零
二、泰勒公式常见题型(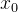 的选取很关键)
的选取很关键)
1.用泰勒公式展开函数
-
方法:对原函数多求几次导,找到规律,写出有规律的式子
-
例子:求函数f(x)=lnx按(x-2)展开的带有佩亚诺型余项的n阶泰勒公式
解:令 ,
,  对f(x)多次求导,又对
对f(x)多次求导,又对 不断求导找出规律
不断求导找出规律


 ……
……
 ,将x=2带入式子,然后写出泰勒展开式
,将x=2带入式子,然后写出泰勒展开式



2.用泰勒公式求极限
2.再观察分子分母中哪些式子需要用泰勒展开
3.展开时泰勒公式中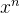 与原式中本身次方最大的
与原式中本身次方最大的 的关系为n<=m
的关系为n<=m
4.注意可以转换的式子如 ,再对
,再对 用泰勒公式展开
用泰勒公式展开
5.展开时注意是否可以自变量整体代换如  ,我们知道常用的
,我们知道常用的 的泰勒展开式,可以直接用1/x替换x,前提是用来替换的式子必须趋近于零
的泰勒展开式,可以直接用1/x替换x,前提是用来替换的式子必须趋近于零
-
例题1:求极限
 (提示:对cosx泰勒展开,对
(提示:对cosx泰勒展开,对 ,由常见
,由常见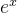 泰勒展开,用
泰勒展开,用  整体代换
整体代换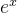 展开式中的x,两项展开式中x最大次方应该 <=4,最后答案为
展开式中的x,两项展开式中x最大次方应该 <=4,最后答案为 )
)
-
例题2:求极限
 (提示:使用等价无穷小的替换,再对
(提示:使用等价无穷小的替换,再对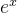 用泰勒展开,最后答 案为2)
用泰勒展开,最后答 案为2)
-
例题3:求极限
![\lim_{x\rightarrow +\infty }{\frac{e}{2}}x+x^{2}[ (1+\frac{1}{x})^{x}-e]](https://latex.csdn.net/eq?%5Clim_%7Bx%5Crightarrow%20+%5Cinfty%20%7D%7B%5Cfrac%7Be%7D%7B2%7D%7Dx+x%5E%7B2%7D%5B%20%281+%5Cfrac%7B1%7D%7Bx%7D%29%5E%7Bx%7D-e%5D)
解:由泰勒公式![(1+\frac{1}{x})^{x}=e^{xln^{(1+\frac{1}{x})}}=e^{x[\frac{1}{x}-{\frac{1}{2x^{2}}}+\frac{1}{3x^{3}}+\circ (\frac{1}{x^{3}})]}=e^{1-\frac{1}{2x}+\frac{1}{3x^{2}}+\circ (\frac{1}{x^{2}})}](https://latex.csdn.net/eq?%281+%5Cfrac%7B1%7D%7Bx%7D%29%5E%7Bx%7D%3De%5E%7Bxln%5E%7B%281+%5Cfrac%7B1%7D%7Bx%7D%29%7D%7D%3De%5E%7Bx%5B%5Cfrac%7B1%7D%7Bx%7D-%7B%5Cfrac%7B1%7D%7B2x%5E%7B2%7D%7D%7D+%5Cfrac%7B1%7D%7B3x%5E%7B3%7D%7D+%5Ccirc%20%28%5Cfrac%7B1%7D%7Bx%5E%7B3%7D%7D%29%5D%7D%3De%5E%7B1-%5Cfrac%7B1%7D%7B2x%7D+%5Cfrac%7B1%7D%7B3x%5E%7B2%7D%7D+%5Ccirc%20%28%5Cfrac%7B1%7D%7Bx%5E%7B2%7D%7D%29%7D) 对转换后 的式子提出一个e,得到
对转换后 的式子提出一个e,得到![e\cdot e^{[-\frac{1}{2x}+\frac{1}{3x^{2}}+\circ (\frac{1}{x^{2}})]}](https://latex.csdn.net/eq?e%5Ccdot%20e%5E%7B%5B-%5Cfrac%7B1%7D%7B2x%7D+%5Cfrac%7B1%7D%7B3x%5E%7B2%7D%7D+%5Ccirc%20%28%5Cfrac%7B1%7D%7Bx%5E%7B2%7D%7D%29%5D%7D) ,此时对
,此时对![e^{[-\frac{1}{2x}+\frac{1}{3x^{2}}+\circ (\frac{1}{x^{2}})]}](https://latex.csdn.net/eq?e%5E%7B%5B-%5Cfrac%7B1%7D%7B2x%7D+%5Cfrac%7B1%7D%7B3x%5E%7B2%7D%7D+%5Ccirc%20%28%5Cfrac%7B1%7D%7Bx%5E%7B2%7D%7D%29%5D%7D) 用麦克劳林展 开,将
用麦克劳林展 开,将![[-\frac{1}{2x}+\frac{1}{3x^{2}}+\circ (\frac{1}{x^{2}})]](https://latex.csdn.net/eq?%5B-%5Cfrac%7B1%7D%7B2x%7D+%5Cfrac%7B1%7D%7B3x%5E%7B2%7D%7D+%5Ccirc%20%28%5Cfrac%7B1%7D%7Bx%5E%7B2%7D%7D%29%5D) 整体看做x代入
整体看做x代入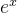 的麦克劳林公式,后续步骤比较简 单,这里不给出解答了,最后答案等于
的麦克劳林公式,后续步骤比较简 单,这里不给出解答了,最后答案等于
(为什么上一步展开到 时不能用整体代入而要先提一个e出来呢?,因为x趋近于无穷,原来的次方
时不能用整体代入而要先提一个e出来呢?,因为x趋近于无穷,原来的次方 是趋近于1的,而不符合麦克劳林的展开条件x趋近于0,当提出e时,后式就可以直接整体代入,用麦克劳林公式展开)
是趋近于1的,而不符合麦克劳林的展开条件x趋近于0,当提出e时,后式就可以直接整体代入,用麦克劳林公式展开)
3.用泰勒公式讨论无穷小的比较
-
方法:统一单位,赋值
-
例题:设
 时,
时, 是比
是比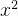 高阶的无穷小,求a和b的值(提示:由题
高阶的无穷小,求a和b的值(提示:由题 ,对
,对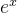 泰勒展开至式子中出现
泰勒展开至式子中出现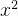 ,再对分母合并同类项,整体等于0,即可求出a、b)
,再对分母合并同类项,整体等于0,即可求出a、b)
4.用泰勒公式证明等式和不等式(重难点)
- 方法:注意
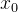 的选取
的选取
1.若只需要证明的结果中不含一阶导数时,可考虑选取题目已知的一阶导数的点或隐含为一阶导数已知的点
2.积分不等式还可考虑选取 ,因为
,因为 积分后可把含
积分后可把含 消去
消去
-
例题1:试证明:若f(x)在[a,b]上存在二阶导数,且
 ,则存在
,则存在 使
使 (想办法用给出的条件构造该函数,选取题目已知的一阶导数的点a,b为分别为
(想办法用给出的条件构造该函数,选取题目已知的一阶导数的点a,b为分别为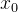 )
)
证明:将 分别在点a,点b泰勒展开得
分别在点a,点b泰勒展开得




令 ,则以上两式相减得
,则以上两式相减得
 ,即证
,即证
-
例题2:设f(x)在[0,1]上二阶可倒,f(0)=f(1)=0,f(x)在[0,1]上的最小值等于-1,试证明至少存在一点
 使
使
证明:由题设存在 ,使f(a)=-1,
,使f(a)=-1, ,对f(x)在a点泰勒展开(即取
,对f(x)在a点泰勒展开(即取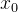 =a),有
=a),有

将x=0,x=1代入上式有




若0<a<1/2,由上式得 , 若1/2<=a<1,由下式得
, 若1/2<=a<1,由下式得 ,故结论成立
,故结论成立
ps:1.想要熟练地掌握泰勒公式并对其加以使用需要琢磨清楚泰勒公式,自己找更多的题练习
2.上述例题摘自《吉米多维奇高等数学练习题》