机器学习笔记1—泰勒展开式和牛顿法

写在前面：自学机器学习的菜鸟一枚，希望通过记录博客的形式来记录自己一点点的进步~ 
下面都是学习过程中自己的一些思考和学习，希望大神们批评指正。

1.1 泰勒展开式

1.1.1泰勒展开式入门

首先，百度了一波，搜到了一个泰勒展开式入门的短短6分钟的视频，好像突然感受到了一点点数学的美。还有发现其实真的没有必要死记公式啊。泰勒展开式的入门浓浓的台湾腔调啊。

---

泰勒公式的表达式：就是下面这个看起来很复杂的公式。 

---

【对于泰勒展开式存在性的一些思考】 
一切事物都是存在即是合理，严密而美好的数学更是如此。 
关于多项式 (x−a)2(x−a)2 
在历史的进程中，多项式是人们最熟悉的函数。对于一些比较复杂的函数，要对这些函数进行处理的时候，我们希望能够近似的将这些函数用我们熟悉的函数来表示。这就是为什么泰勒展开式中会有多项式的成分。当我们可以用这个多项式表示一个函数时，就应该更进一步的思考一下这个多项式之前的系数。

关于系数fn(a)n!fn(a)n! 
这个系数刻画了“一叶知秋”的含义。“一叶知秋”：一片叶子掉下来，就知道秋天来了。 
对于x=a这个点的领域，我们知道了它的一些信息：一阶变化率（知道了函数是增还是减），二阶变化率（知道了是凹还是凸）…..到n阶变化率）通过这些信息，基本就可以想象出这个函数的样子，一点看全的这种感觉。

---

1.1.2 泰勒展开式的推导

下面对泰勒展开式进行推导，这里是学习了[YuanLiangDing的博客](http://blog.sina.com.cn/s/blog_5d323f950101ieyo.html) 
里面介绍的很详细，在这里就不浪费时间敲字了。 
只稍微补充一下文中提到的：从函数的线性近似f(a+Δx)=f(a)+f′(a)Δxf(a+Δx)=f(a)+f′(a)Δx来估计函数值。

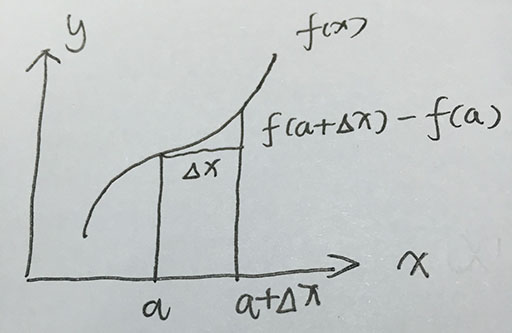
如上图所示（字丑图丑）要估计a点的函数值，我们无法直接代入a来计算。所以就通过取a+Δxa+Δx这一点的函数值，使Δx→0Δx→0时f(a)f(a)和f(a+Δx)f(a+Δx)近似相等。函数在a点的斜率为tanαtan⁡α忘记画出αα了。 
易知 

又有 f′(a)=tanα(3)f′(a)=tan⁡α(3)

将式(3)代入式(2)就得出了线性近似，也就是泰勒的一阶展开：

---

上面的的图片上已经有点函数定积分的几何意义的那个图的感觉了吧。这里就比较好理解为什么泰勒展开式会是由微积分基本定理，就是牛顿莱布尼茨公式通过一系列的换元，转换，得到了泰勒展开式。

---

1.2 牛顿法

这里是学习了luoleicn的专栏里关于牛顿法的文章很通俗易懂。 
总结如下： 
牛顿法主要有两方面的应用： 
1、求方程的根（函数比较复杂，没有求根公式）。 
2、应用于最优化方法求解无约束问题的最优解（通常是求函数的极大极小值）

---

1.2.1 求方程的根

这里马上就用到了刚刚泰勒展开式推导过程中用到的函数的线性近似公式，也就是泰勒公式的一阶展开。

原理：f(a+Δx)=f(a)+f′(a)Δxf(a+Δx)=f(a)+f′(a)Δx

步骤：

(1). 第一步选取初始点，构造一阶泰勒展开式。 
在x0x0处展开到一阶泰勒公式：f(x)=f(x0)+f′(x0)(x−x0)f(x)=f(x0)+f′(x0)(x−x0) 
求解f(x)=0⟹f(x0)+f′(x0)(x−x0)=0f(x)=0⟹f(x0)+f′(x0)(x−x0)=0 
设x1x1是上式的解： 
x1=x0−f′(x0)f(x0)x1=x0−f′(x0)f(x0) 
虽然这个x1x1并不是f(x)=0f(x)=0 的解，但它比f(x0)f(x0)更靠近0。 
(2).迭代公式 
xn+1=xn−f′(xn)f(xn)xn+1=xn−f′(xn)f(xn) 
根据上面公式迭代，必定能找到一个x∗x∗使得f(x∗)→0f(x∗)→0。

---

1.2.2 求最优化方法（非线性函数的无约束问题）

1、二维情况 
任务：优化目标函数ff,通常是求ff的极大极小值的问题。（基本所有的最优化问题都可以用minf(x)的问题minf(x)的问题来描述）

---

补充： 
(1) 函数极小值的一阶必要条件：若x∗∈Dx∗∈D是一个极小点，则必有f′(x∗)=0f′(x∗)=0 
(2) 函数极小值的二阶必要条件：若x∗∈Dx∗∈D是一个极小点，则必有f′(x∗)=0f′(x∗)=0&&f′′(x∗)>0f″(x∗)>0

---

所以求ff的极小值问题可以转换为求f′(x)=0f′(x)=0的解的问题。这就可以转化为上面的求方程根的方法了。 
对目标函数进行二次函数近似： 
f′(x)=0⟹f′(x0)+f′′(x0)(x1−x0)=0f′(x)=0⟹f′(x0)+f″(x0)(x1−x0)=0 
⟹x1=x0−f′(x0)f′′(x0)⟹x1=x0−f′(x0)f″(x0) 
⇓⇓ 
推出迭代公式： xn+1=xn−f′(xn)f′′(xn)xn+1=xn−f′(xn)f″(xn)

正规来说就是对函数f(x)f(x)进行二阶泰勒展开： 
原理：f(a+Δx)=f(a)+f′(a)Δx+12f′′(x)Δx2f(a+Δx)=f(a)+f′(a)Δx+12f″(x)Δx2 
对函数f(x)f(x)近似二次函数近似。 
f(x)=f(xa)+f′(xa)(x−xa)+12f′′(xa)(x−xa)2f(x)=f(xa)+f′(xa)(x−xa)+12f″(xa)(x−xa)2 
求解f′(x)=0⟹{f(xa)+f′(xa)(x−xa)+12f′′(xa)(x−xa)2}′=0f′(x)=0⟹{f(xa)+f′(xa)(x−xa)+12f″(xa)(x−xa)2}′=0

2、高维度 
这里x就不是简单的一个数字了，而是一个矩阵，更应该说是一个n维的列向量。 
推导过程和上面类似，这里我对包含矩阵的函数的求导还没有思考清楚，就贴上公式吧 
之后再具体学习一下。 
Xn+1=Xn−G−1kgkXn+1=Xn−Gk−1gk

---

2015/10/29 first version

---

推导高维度的牛顿公式： 
f(X),Xf(X),X为n维列向量，表示含有n个变量。 

对 f(X)f(X) 在 XkXk 处泰勒二阶展开。 
函数为二维时的展开公式： f(x)=f(xk)+f′(xk)(x−xk)+12f′′(xk)(x−xk)2f(x)=f(xk)+f′(xk)(x−xk)+12f″(xk)(x−xk)2  
相应的高维展开式如下： 





可以看出 ∇f(X)∇f(X) 和 X−XkX−Xk 都是列向量，无法相乘取内积。所以这里要将 gkgk 转置。后面的 （X−Xk）2（X−Xk）2 也是一样的道理。 
所以对于高维函数的泰勒展开式为： 

接着就应该求解 f′(X)=0f′(X)=0  
这里就涉及到矩阵求导问题，先贴出我的参考链接 矩阵向量求导法则  
对 f(X)f(X) 求导时，就不要写成泰勒展开式的形式了，直接写成二维函数那个样子。我把它拆分为三部分。 
f(X)1=f(Xk)f(X)1=f(Xk)  
f(X)2=f′(Xk)(X−Xk)f(X)2=f′(Xk)(X−Xk)  
f(X)3=12f′′(Xk)(X−Xk)2f(X)3=12f″(Xk)(X−Xk)2  
（1） 对 f(X)1f(X)1 求导， f(Xk)f(Xk) 不含有变量 XX 所以此项导数为0。 
（2） 对 f(X)2f(X)2 求导。 
gTkgkT 不含有变量 XX 所以为常数，不需要考虑，这时要求导的部分变成了 y=(X−Xk)y=(X−Xk) 。 
为简便，我设X为3维的列向量 

yy 对 XX 求导： yy 为矩阵 XX 为列向量。属于矩阵对列向量求导的那一类。 
根据求导公式： 

对于 ∂y1∂X∂y1∂X 是 y1=x1−xk1y1=x1−xk1 对 XX 求导，属于元素对列向量求导的类型。 
根据求导公式： 

同理可知


所以  f′(X)2=f′(Xk)=gkf′(X)2=f′(Xk)=gk  
（3） 对 f(X)3f(X)3 求导。 
与上一步类似。 
f′(X)3=f′′(Xk)=Gkf′(X)3=f″(Xk)=Gk  
所以：  f′(X)=gk+Gk(X−Xk)=0f′(X)=gk+Gk(X−Xk)=0  
若 GkGk 为非奇异（则矩阵可逆），解这个方程，记其解为 Xk+1Xk+1 即得牛顿法的迭代公式： 
Xk+1=Xk−G−1kgkXk+1=Xk−Gk−1gk

---

2015/11/3 second version