机器学习算法中，有一个基础的算法，线性回归，它的目的是求出一条直线，满足所有点到这条直线的距离最短，也就是这些数据点能够看起来都在这条直线附近，最后，可以根据这条直线来预测其他数据的值。
线性回归，最推荐的做法其实是使用梯度下降算法，这种算法比较通用，对数据要求不高，可以离散不连续。如下所示，是一个使用梯度下降算法来进行线性回归的示例：
准备数据：
这两列数据最后是放在lineardata.csv中的，分别对应x,y集合。
1 3
1.2 3
1.2 4
1.5 4.5
1.6 4.3
6.5 12
3.6 7.1
2.5 9
5.7 14
6 11
9 17
8.9 17
7.1 15
7 14
2.5 4
0.8 2
0.5 2
3.4 7
3.6 9
5.6 12
6.7 15
6.9 15
7.1 14
7.5 17
7.8 16
8.1 15
8.3 15
8.5 15
8.7 16
8.7 17
8.8 18
8.8 20
8 16
9 19
9.2 18
10.1 20
1.1 3.2
1.6 4.2
4 9
12 25
9.5 20
程序代码：
import numpy as np
import matplotlib.pyplot as plt
def loss_error(w, b, data):
x = data[:, 0]
y = data[:, 1]
loss = np.sum((y - w * x - b) ** 2) / data.shape[0]
return loss
def linear_gradient(w, b, data, lr):
N = float(len(data))
x = data[:, 0]
y = data[:, 1]
dw = np.sum(-(2 / N) * x * (y - w * x - b))
db = np.sum(-(2 / N) * (y - w * x - b))
w = w - (lr * dw)
b = b - (lr * db)
return w, b
def optimizer(data, w, b, lr, epoch):
for i in range(epoch):
w, b = linear_gradient(w, b, data, lr)
if i % 100 == 0:
print('epoch {0}:loss={1}'.format(i, loss_error(w, b, data)))
return w, b
def plot_data(data, w, b):
x = data[:, 0]
y = data[:, 1]
y_predict = w * x + b
plt.plot(x, y, 'o')
plt.plot(x, y_predict, 'k-')
plt.show()
def linear_regression():
data = np.loadtxt('lineardata.csv', delimiter=',')
# data = pd.read_csv('lineardata.csv',encoding='utf8')
x = data[:, 0]
y = data[:, 1]
plt.plot(x, y, 'o')
#plt.show()
lr = 0.01
epoch = 1000
w = 0.0
b = 0.0
print("initial variables:\n initial_b={0}\n initial_w={1}\n loss={2}\n".format(b, w, loss_error(w, b, data)))
w, b = optimizer(data, w, b, lr, epoch)
print('final formula parameters:\n b = {0}\n w={1} \n loss={2}\n'.format(b, w, loss_error(w, b, data)))
plot_data(data, w, b)
if __name__ == '__main__':
linear_regression()运行，打印结果：
initial variables:
initial_b=0.0
initial_w=0.0
loss=184.68365853658537
epoch 0:loss=3.265436338536489
epoch 100:loss=1.4187213286545117
epoch 200:loss=1.3652986742281288
epoch 300:loss=1.3437697330412992
epoch 400:loss=1.3350937263246236
epoch 500:loss=1.3315973587190568
epoch 600:loss=1.330188348003359
epoch 700:loss=1.329620526932774
epoch 800:loss=1.3293916991711343
epoch 900:loss=1.3292994832474747
final formula parameters:
b = 1.2393038013472177
w=1.8672419688724071
loss=1.3292625499252577同时，画出的图形：
我们这里重点关注最后计算出来的系数w,b，他们分别是 w=1.8672419688724071， b = 1.2393038013472177，后面通过最小二乘法计算来做对别。
============================================
下面开始这篇文章的主题，最小二乘法。
在最小二乘法之前，人们知道，让一些离散的数据点靠近一条直线，可以通过求距离的办法，但是距离是作减法，结果有正，有负，最后其实是计算绝对值的和最小。
最小二乘法最早是由法国科学家勒让德发明的，但是当时没有人知道，直到高斯提供了最小二乘法优化方法强于其他方法的证明才被世人知道。
最小二乘法是计算差值的平方和最小。
假定拟合直线为 y = wx + b ，最小二乘法就是要求公式：
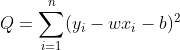最小值。
一般使用求导法。分别对w,b求导：
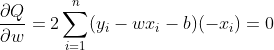(1)
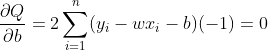(2)
这里分别要求出w,b的值。上面的公式中（2）中，可以把求和公式展开，得到：
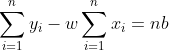
进而求出b, 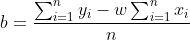(3) ，将b带入（1）式，求出w。
求出了w,那么再计算b就容易了。一般直接使用上面推导的公式(3)表示。
下面，我们通过java语言编写算法来实现最小二乘法：
package mr;
public class LeastSquareMethod {
private static double w;
private static double b;
private static int n;
public static void fit(double[] x,double[] y){
n = x.length<y.length?x.length:y.length;
double xy = 0,xT = 0,yT = 0,xS = 0;
for(int i=0;i<n;i++){
xy+=x[i]*y[i];
xT += x[i];
yT += y[i];
xS += Math.pow(x[i],2);
}
w = (n*xy-xT*yT)/(n*xS-Math.pow(xT,2));
b = yT/n - w*xT/n;
}
public static double predict(double x){
System.out.println("w="+w);
System.out.println("b="+b);
return w*x + b;
}
public static void main(String[] args) {
double[] x = {1,1.2,1.2,1.5,1.6,6.5,3.6,2.5,5.7,6,9,8.9,7.1,7,2.5,0.8,0.5,3.4,3.6,5.6,6.7,6.9,7.1,7.5,7.8,8.1,8.3,8.5,8.7,8.7,8.8,8.8,8,9,9.2,10.1,1.1,1.6,4,12,9.5};
double[] y = {3,3,4,4.5,4.3,12,7.1,9,14,11,17,17,15,14,4,2,2,7,9,12,15,15,14,17,16,15,15,15,16,17,18,20,16,19,18,20,3.2,4.2,9,25,20};
fit(x,y);
System.out.println(predict(15));
}
}程序运行结果：
w=1.8658557134722435
b=1.2497797817573275
29.237615483840983这个结果跟上面梯度下降计算的直线系数，w=1.8672419688724071， b = 1.2393038013472177,很接近，但是有一些差别。
最小二乘法公式里面，还有一个隐含的公式就是：
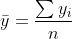和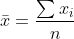
，这两个很好理解，就是y的平均数=
，x的平均数 =
。
所以把这两个公式代入上面w的表达式，可以计算出另一个w,b的表达式：
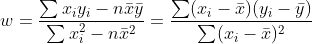(4)
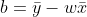
公式（4）中的分子推导如下：
分母的推导如下：
根据公式（4），我们有另一种计算最小二乘法直线系数的算法：
package mr;
import org.apache.commons.math3.stat.descriptive.moment.Mean;
public class LeastSquareMethod2 {
private double[] x;
private double[] y;
public LeastSquareMethod2(double[] x, double[] y){
this.x = x;
this.y = y;
}
public double[] getRegressionModel(){
if(x.length!=y.length)
return null;
Mean meanUtil = new Mean();
double xmean = meanUtil.evaluate(x);
double ymean = meanUtil.evaluate(y);
double numerator = 0d;
double denominator = 0d;
for(int i=0;i<x.length;i++){
double xi = x[i];
double yi = y[i];
numerator = numerator+(xi-xmean)*(yi-ymean);
denominator = denominator+(xi-xmean)*(xi-xmean);
}
double w = numerator/denominator;
double b = ymean - w*xmean;
double[] model = {w,b};
return model;
}
public static void main(String[] args) {
double[] x = {1,1.2,1.2,1.5,1.6,6.5,3.6,2.5,5.7,6,9,8.9,7.1,7,2.5,0.8,0.5,3.4,3.6,5.6,6.7,6.9,7.1,7.5,7.8,8.1,8.3,8.5,8.7,8.7,8.8,8.8,8,9,9.2,10.1,1.1,1.6,4,12,9.5};
double[] y = {3,3,4,4.5,4.3,12,7.1,9,14,11,17,17,15,14,4,2,2,7,9,12,15,15,14,17,16,15,15,15,16,17,18,20,16,19,18,20,3.2,4.2,9,25,20};
LeastSquareMethod2 leastSquareMethod2 = new LeastSquareMethod2(x,y);
double[] model = leastSquareMethod2.getRegressionModel();
System.out.println("w=" + model[0]);
System.out.println("b=" + model[1]);
}
}打印结果：
w=1.8658557134722438
b=1.2497797817573257这个结果跟上面算法结果高度接近。只有w结果最后一位有差别。
这篇文章通过机器学习算法中线性回归的实例，分别使用梯度下降和最小二乘法来计算，效果很接近，一般而言，梯度下降使用的更广泛一些，但是最小二乘法对于这类线性回归也是适合的。
最小二乘法的这套公式推导，使用了求导数，求和运算，不管怎么样，这里要计算出w,b两个未知数，需要两个方程。最后根据公式计算出w,b的值，同时根据平均数的计算公式，我们又推导了另一种表示方法，他们是等价的。