在之前的一篇博客机器学习中的数学(7)——PCA的数学原理中深入讲解了，PCA的数学原理。谈到PCA就不得不谈LDA，他们就像是一对孪生兄弟，总是被人们放在一起学习，比较。这这篇博客中我们就来谈谈LDA模型。由于水平有限，积累还不够，有不足之处还望指点。下面就进入正题吧。
前面的博客提到PCA是常用的有效的数据降维的方法，与之相同的是LDA也是一种将数据降维的方法。PCA已经是一种表现很好的数据降维的方法，那为什么还要有LDA呢？下面我们就来回答这个问题？
PCA是一种无监督的数据降维方法，与之不同的是LDA是一种有监督的数据降维方法。我们知道即使在训练样本上，我们提供了类别标签，在使用PCA模型的时候，我们是不利用类别标签的，而LDA在进行数据降维的时候是利用数据的类别标签提供的信息的。
从几何的角度来看，PCA和LDA都是讲数据投影到新的相互正交的坐标轴上。只不过在投影的过程中他们使用的约束是不同的，也可以说目标是不同的。PCA是将数据投影到方差最大的几个相互正交的方向上，以期待保留最多的样本信息。样本的方差越大表示样本的多样性越好，在训练模型的时候，我们当然希望数据的差别越大越好。否则即使样本很多但是他们彼此相似或者相同，提供的样本信息将相同，相当于只有很少的样本提供信息是有用的。样本信息不足将导致模型性能不够理想。这就是PCA降维的目标：将数据投影到方差最大的几个相互正交的方向上。这种约束有时候很有用，比如在下面这个例子： 
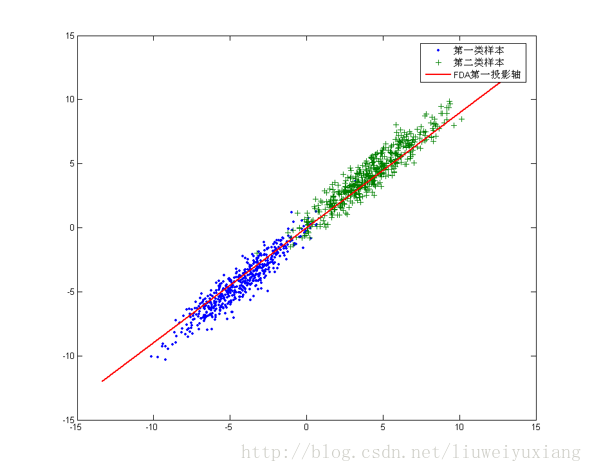
对于这个样本集我们可以将数据投影到x轴或者y轴，但这都不是最佳的投影方向，因为这两个方向都不能最好地反映数据的分布。很明显还存在最佳的方向可以描述数据的分布趋势，那就是图中红色直线所在的方向。也是数据样本做投影，方差最大的方向。向这个方向做投影，投影后数据的方差最大，数据保留的信息最多。
但是，对于另外的一些不同分布的数据集，PCA的这个投影后方差最大的目标就不太合适了。比如对于下面图片中的数据集： 
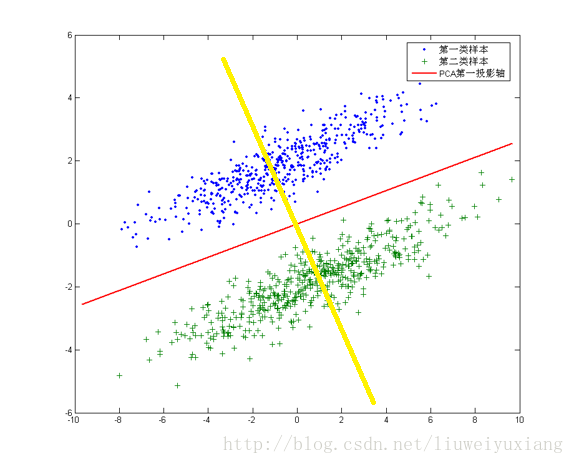
针对这个数据集，如果同样选择使用PCA，选择方差最大的方向作为投影方向，来对数据进行降维。那么PCA选出的最佳投影方向，将是图中红色直线所示的方向。这样做投影确实方差最大，但是是不是有其他问题。聪明的你一定发现了，这样做投影之后两类数据样本将混合在一起，将不再线性可分，甚至是不可分的。这对我们来说简直就是地狱，本来线性可分的样本被我们亲手变得不再可分。
帅气英俊的你也一定发现了，图中还有一条耀眼的黄色直线，向这条直线做投影即能使数据降维，同时还能保证两类数据仍然是线性可分的。上面的这个数据集如果使用LDA降维，找出的投影方向就是黄色直线所在的方向。
这其实就是LDA的思想，或者说LDA降维的目标：将带有标签的数据降维，投影到低维空间同时满足三个条件：
其实第二个和第三个条件是基本等价的，我们很容易想到，使样本尽可能好分的投影方向，就是要使投影后使得同类样本尽可能近，不同类样本尽可能远。
上面大致讲解的LDA的基本思想，以及与PCA的不同，下面就来介绍一下LDA模型。
LDA模型实现基本思想是和PCA相同的，都是向低维空间做投影，所以对于向量投影的基本的知识，这里就不再进行讲解了，不懂得同学可以参看文章开头提到的那篇PCA的博客。
为什么是线性判别分析呢？所谓的线性就是，我们要将数据点投影到直线上（可能是多条直线），直线的函数解析式又称为线性函数。通常直线的表达式为
y=wTxy=wTx
其实这里的x就是样本向量（列向量），如果投影到一条直线上w就是一个特征向量（列向量形式）或者多个特征向量构成的矩阵。至于w为什么是特征向量，后面我们就能推导出来。y为投影后的样本点（列向量）。
我们首先使用两类样本来说明，然后再推广至多类问题。
将数据投影到直线w上，则两类样本的中心在直线上的投影分别为wTμ0wTμ0和wTμ1wTμ1，若将所有的样本点都都投影到直线上，则两类样本的协方差分别为wT∑0wwT∑0w和wT∑1wwT∑1w.
投影后同类样本协方差矩阵的求法：
∑x∈Di(wTx−wTui)2=∑x∈Di(wT(x−ui))2=∑x∈DiwT(x−μi)(x−ui)Tw=wT∑x∈Di[(x−μi)(x−ui)T]w∑x∈Di(wTx−wTui)2=∑x∈Di(wT(x−ui))2=∑x∈DiwT(x−μi)(x−ui)Tw=wT∑x∈Di[(x−μi)(x−ui)T]w
上式的中间部分∑x∈Di(x−μi)(x−ui)T∑x∈Di(x−μi)(x−ui)T便是同类样本投影前的协方差矩阵。由还可以看出同类样本投影前后协方差矩阵之间的关系。如果投影前的协方差矩阵为ΣΣ 则投影后的为 wTΣwwTΣw.
上式的推导需要用到如下公式：a,ba,b 都是列向量，(a⋅b)2=(aTb)2=(aTb)(aTb)=(aTb)(aTb)T=aTbbTa(a⋅b)2=(aTb)2=(aTb)(aTb)=(aTb)(aTb)T=aTbbTa .
欲使同类样例的投影点尽可能接近，可以让同类样本点的协方差矩阵尽可能小，即wT∑0w+wT∑1wwT∑0w+wT∑1w 尽可能小; 而欲使异类样例的投影点尽可能远离，可以让类中心之间的距离尽可能大，即||wTμ0−wTμ1||22||wTμ0−wTμ1||22 尽可能大。同时考虑二者，则可得到欲最大化的目标
J=||wTμ0−wTμ1||22wT(∑0+∑1)w=wT(μ0−μ1)(μ0−μ1)TwwT(∑0+∑1)wJ=||wTμ0−wTμ1||22wT(∑0+∑1)w=wT(μ0−μ1)(μ0−μ1)TwwT(∑0+∑1)w
上式中的||⋅||||⋅||表示欧几里得范数，||x−μi||2=(x−μi)T(x−μi)||x−μi||2=(x−μi)T(x−μi)
上面的这段话来自于周志华老师的机器学习书籍，不知道大家对上面的这段话是否存在疑问? 我在阅读 的时候是存在疑问的，即为什么同类样本点的协方差矩阵尽可能小，同类样例的投影点就尽可能接近。我想大概是这样的：我们在最初接触协方差是用来表示两个变量的相关性，我们来看一下协方差和方差的公式：
cov=1n∑(X−X¯)(Y−Y¯)cov=1n∑(X−X¯)(Y−Y¯)
cov=1n∑(X−X¯)(X−X¯)cov=1n∑(X−X¯)(X−X¯)
可以看到协方差的公式和方差十分相近，甚至可以说方差是协方差的一种特例。我们知道方差可以用来度量数据的离散程度，(X−X¯)(X−X¯)越大，表示数据距离样本中心越远，数据越离散，数据的方差越大。同样我们观察，协方差的公式，(X−X¯)(X−X¯)和(Y−Y¯)(Y−Y¯)越大，表示数据距离样本中心越远，数据分布越分散，协方差越大。相反他们越小表示数据距离样本中心越近，数据分布越集中，协方差越小。
所以协方差不仅是反映了变量之间的相关性，同样反映了多维样本分布的离散程度(一维样本使用方差)，协方差越大（对于负相关来说是绝对值越大），表示数据的分布越分散。所以上面的“欲使同类样例的投影点尽可能接近，可以让同类样本点的协方差矩阵尽可能小”就可以理解了。
类间散度矩阵其实就是协方差矩阵乘以样本数目，即散度矩阵与协方差矩阵只是相差一个系数。对于协方差矩阵和散度矩阵有疑问的同学可以参考博文：机器学习中的数学(3)——协方差矩阵和散布（散度）矩阵
对于两类样本而言：
Sb=(μ0−μ1)(μ0−μ1)TSb=(μ0−μ1)(μ0−μ1)T
对于多类问题，类间散度矩阵公式：
Sb=∑i=1C(μi−μ)(μi−μ)TSb=∑i=1C(μi−μ)(μi−μ)T
表示各个类样本均值的协方差矩阵。
如果我们只使用这样一个类间散度矩阵这样一个约束条件来对数据进行降维：即使得类间的样本投影后尽可能远离。那么参考PCA的降维过程：
Sbu=λuSbu=λu
不同的是，为了保证类间的样本投影后尽可能远离，我们应该选择特征值最大的特征向量代表的方向做投影。这样才能保证，不同类样本投影之后方差尽可能地大，尽可能能地远离。
对于两类问题而言：
Sw=Σ0+Σ1=∑x∈D0(x−μ0)(x−u0)T+∑x∈D1(x−μ1)(x−u1)TSw=Σ0+Σ1=∑x∈D0(x−μ0)(x−u0)T+∑x∈D1(x−μ1)(x−u1)T
对于多类问题类内散度矩阵公式：
Sw=∑i=1C∑j=1Mi(xji−μi)(xji−μ1)TSw=∑i=1C∑j=1Mi(xij−μi)(xij−μ1)T
其中：
∑j=1Mi(xji−μi)(xji−μi)T∑j=1Mi(xij−μi)(xij−μi)T
表示第i类样本的协方差矩阵。所以SwSw就是表示C类样本协方差矩阵之和。
如果我们只使用这样一个类内散度矩阵这样一个约束条件来对数据进行降维：即使得类内的样本投影后尽可能接近。那么参考PCA的降维过程：
Swu=λuSwu=λu
不同的是，为了保证类内的样本投影后尽可能接近，我们应该选择特征值最小的特征向量代表的方向做投影。这样才能保证，同类样本投影之后方差尽可能地小，尽可能能地接近。
定义过类内散度矩阵和类间散度矩阵后，我们可以将上述的优化目标重新写为：
J=wTSbwwTSwwJ=wTSbwwTSww
这就是LDA欲最大化的目标，即SbSb与SwSw的广义瑞利商。
如何确定ww呢？注意到上式的分子和分母都是关于ww的二次项，因此上式的解与ww的长度无关,只与其方向有关.不失一般性，令wTSww=1wTSww=1,则上式等价于：
minw−wTSbwminw−wTSbw
st.wTSww=1st.wTSww=1
使用拉格朗日乘子法,(对于拉格朗日乘子法不太了解的同学可以参考博文：机器学习中的数学(5)——拉格朗日乘子法和KKT条件)上式等价于：
c(w)=wTSbw−λ(wTSww−1)c(w)=wTSbw−λ(wTSww−1)
dcdw=2Sbw−2λSww=0dcdw=2Sbw−2λSww=0
Sbw=λSwwSbw=λSww
S−1wSbw=λwSw−1Sbw=λw
可以看到上式就有转化为一个求解特征值和特征向量的问题了。w就是我们要求解的特征向量，这就验证了我们之前所说的式子y=wTxy=wTx中的w就是特征向量构成的矩阵。
但是到这里我们仍然有个问题需要解决，那就是SwSw是否可逆。遗憾的是在实际的应用中，它通常是不可逆的，我们通常有连个办法解决该问题。
解决方法一：
令Sw=Sw+γISw=Sw+γI, 其中γγ是一个特别小的数，这样SwSw一定可逆。
解决方法二：
先使用PCA对数据进行降维，使得在降维后的数据上SwSw可逆，在使用LDA。
1.机器学习-线性判别分析.周志华x
2.机器学习中的数学(4)-线性判别分析（LDA）, 主成分分析(PCA)
LDA算法流程
现在我们对LDA降维的流程做一个总结。
输入：数据集D={(x1,y1),(x2,y2),...,((xm,ym))},其中任意样本xi为n维向量，yi∈{C1,C2,...,Ck}，降维到的维度d。
输出：降维后的样本集$D′$
1) 计算类内散度矩阵Sw
2) 计算类间散度矩阵Sb
3) 计算矩阵Sw^−1*Sb
4）计算Sw^−1*Sb的最大的d个特征值和对应的d个特征向量(w1,w2,...wd),得到投影矩阵W
5) 对样本集中的每一个样本特征xi,转化为新的样本zi=WT*xi
6) 得到输出样本集
线性判别分析（Linear Discriminant Analysis, LDA）是一种有监督降维方法，有关机器学习的书上一定少不了对 PCA 和 LDA 这两个算法的介绍。LDA 的标准建模形式是这样的（这里以两类版本为例，文章会在几个关键点上讨论多类情况）：
其中，
是类间散布矩阵，
是类内散布矩阵， w 是投影直线：
怎么样，一定非常熟悉吧，经典的 LDA 就是长这个样子的。这个式子的目标也十分直观：将两类样本投影到一条直线上，使得投影后的类间散布矩阵与类内散布矩阵的比值最大。
三个加粗的词隐含着三个问题：
1. 为什么是类间散布矩阵
呢？直接均值之差 m1-m2 不是更符合直觉吗？这样求出来的解和原来一样吗？
2. 为什么是投影到直线，而不是投影到超平面？PCA 是把 d 维样本投影到 c 维 (c<d)，LDA 为什么不能也投影到 c 维，而是直接投影到 1 维呢？同样地，在 K 类 LDA 中，为什么书上写的都是投影到 K-1 维，再高一点不行吗？这是必然吗？
3. 为什么是类间散布与类内散布的比值呢？差值不行吗？
这篇文章就围绕这三个问题展开。我们先回顾一下经典 LDA 的求解，然后顺次讲解分析这三个问题。
原问题等价于这个形式：
然后就可以用拉格朗日乘子法了：
求导并令其为 0：
得到解：
对矩阵
进行特征值分解就可以得到 w。但是有更简单的解法：
而其中
是一个标量，所以
和 λw 共线，得到：
求解完毕。非常优雅，不愧是教科书级别的经典算法，整个求解一气呵成，标准的拉格朗日乘子法。但是求解中还是用到了一个小技巧：
是标量，从而可以免去特征值分解的麻烦。
那么，我们能不能再贪心一点，找到一种连这个小技巧都不需要的求解方法呢？答案是可以，上面的问题在下一节中就能得到解决。
我们不用类内散布矩阵
了，改用均值之差 m1-m2 这个更符合直觉的东西：
还是用拉格朗日乘子法：
求导并令其为 0：
得到解：
怎么样，是不是求解更简单了呢？不需要任何技巧，一步一步下来就好了。
为什么说均值之差更符合直觉呢？大家想啊，LDA 的目的是让投影后的两类之间离得更远，类内离得更近。说到类内离得更近能想到的最直接的方法就是让类内方差最小，这正是类内散布矩阵；说到类间离得更远能想到的最直接的方法肯定是让均值之差最大，而不是均值之差与自己的克罗内克积这个奇怪的东西最大。
那么经典 LDA 为什么会用类间散布矩阵呢？我个人认为是这样的表达式看起来更加优雅：分子分母是齐次的，并且这个东西恰好就是广义瑞利商：
虽然经典 LDA 求解没有上面这个方法直接，但是问题表述更加规范，所用到的技巧也非常简单，不会给是使用者带来困扰，所以 LDA 最终采用的就是类间散布矩阵了吧。
上面那个问题只算是小打小闹，没有太大的意义，但是这个问题就很有意义了：LDA 为什么直接投影到直线（一维），而不能像 PCA 一样投影到超平面（多维）呢？ 我们试试不就完了。
假设将样本投影到
上，其中每一个 wi 都是经典 LDA 中的 w 。也就相当于我们不是把样本投影到一条直线上，而是投影到 c 条直线上，也就相当于投影到了超平面上。投影后的样本坐标为：
所以样本的投影过程就是：
那么，均值的投影过程也是这样：
投影后的均值之差的二范数：
为什么不用第一行的向量内积而偏要用第二行的迹运算呢？因为这样可以拼凑出类间散布
来，和经典 LDA 保持形式的一致。
回顾一下经典 LDA 的形式：
现在我们有了
，还缺个约束，类比一下就可以得到
了：
实际上，约束也可以选择成
，这两个约束实际上都是在限制 W 的解空间，得出来的解是等价的，这两个约束有什么区别呢？我只发现了一点：
回想
是 c 条投影直线，为了确保向这 c 条直线投影能等价于向 c 维子空间投影，我们需要保证 c 条直线是线性无关的，即 rank(W) =c。看一下约束：
右边是秩为 c 的单位矩阵，因为矩阵乘积的秩不大于每一个矩阵的秩，所以左边这三个矩阵的秩都要不小于 c，因此我们得到了 rank(W) = c。也就是说，
能够保证我们在向一个 c 维子空间投影。而约束
中没有显式地表达这一点。
我对矩阵的理解还不够深入，不知道
是否也隐含了对秩的约束，所以为了保险起见，我选择了带有显式秩约束的
，这样就得到了我们的高维投影版 LDA：
下面来求解这个问题。还是拉格朗日乘子法：
求导并令其为 0：
得到了：
在大部分情况下，一些协方差矩阵的和
是可逆的。即使不可逆，上面这个也可以用广义特征值问题的方法来求解，但是这里方便起见我们认为
可逆：
我们只要对
进行特征值分解，就可以得到 d 个特征向量了，挑出最大特征值对应的 c 个特征向量来组成 W，我们不就得到向 c 维子空间的投影了吗？
真的是这样吗？
不是这样的。诚然，我们可以选出 c 个特征向量，但是其中只有 1 个特征向量真正是我们想要的，另外 c-1 个没有意义。
观察：
发现了吗？等式右边的 (m1-m2) 是一个向量，换句话说，是一个秩为 1 的矩阵。那么，这个乘积的秩也不能大于 1，并且它不是 0 矩阵，所以：
秩为 1 的矩阵只有 1 个非零特征值，也只有 1 个非零特征值对应的特征向量 w。
可能有人会问了，那不是还有零特征值对应的特征向量吗，用它们不行吗？
不行。来看一下目标函数：
我们刚才得到的最优性条件：
所以目标函数为：
而我们的 W 只能保证 λ1, λ2, ..., λd 中的一个非零，无论我们怎么选取剩下的 c-1 个 w，目标函数也不会再增大了，因为唯一一个非零特征值对应的特征向量已经被选走了。
所以，两类 LDA 只能向一条直线投影。
这里顺便解释一下 K 类 LDA 为什么只能投影到 K-1 维，其实道理是一样的。K 类 LDA 的类间散布矩阵是：
可以看出，
是 K 个秩一矩阵
的和（因为 mk-m 是秩一的向量），所以它的秩最大为 K。并且
，所以这 K 项中有一项可以被线性表出。所以，
的秩最大为 K-1。也即：
只有 K-1 个非零特征值。所以，K 类 LDA 最高只能投影到 K-1 维。
咦？刚才第三个问题怎么提的来着，可不可以不用比值用差值，用差值的话会不会解决这个投影维数的限制呢？
经典 LDA 的目标函数是投影后的类间散布与类内散布的比值，我们很自然地就会想，为什么非得用比值呢，差值有什么不妥吗？ 再试试不就完了。
注意，这一节我们不用向量 w，而使用矩阵 W 来讨论，这也就意味着我们实际上在同时讨论二类 LDA 和多类 LDA，只要把
和
换成对应的就好了。
注意到可以通过放缩 W 来得到任意大的目标函数，所以我们要对 W 的规模进行限制，同时也进行秩限制：
也就得到了差值版的 LDA：
依然拉格朗日乘子法：
求导并令其为 0：
得到了：
由
，有：
可以得到：
若括号内的东西可逆，则上式可以写为：
注意到， 
的秩不大于 K-1，说明等号左边的秩不大于 K-1，那么等号右边的秩也不大于 K-1，即：
所以我们还是会遇到秩不足，无法求出 K-1 个以上的非零特征值和对应的特征向量。这样还不够，我们还需要证明的一点是，新的目标函数在零特征值对应的特征向量下依然不会增加。
目标函数（稍加变形）为：
再利用刚才我们得到的最优性条件（稍加变形）：
所以目标函数为：
结论没有变化，新的目标函数依然无法在零特征值的特征向量下增大。
综合新矩阵依然秩不足和零特征值依然对新目标函数无贡献这两点，我们可以得到一个结论：用差值代替比值也是可以求解的，但是我们不会因此受益。
既然比值和差值算出来的解性质都一样，那么为什么经典 LDA 采用的是比值而不是差值呢？
我个人认为，这可能是因为比值算出来的解还有别的直觉解释，而差值的可能没有，所以显得更优雅一些。什么直觉解释呢？
在二分类问题下，经典 LDA 是最小平方误差准则的一个特例。若让第一类的样本的输出值等于 N/N1 ，第二类样本的输出值等于 -N/N2 ， N 代表相应类样本的数量，然后用最小平方误差准则求解这个模型，得到的解恰好是（用比值的）LDA 的解。这个部分 PRML 上有讲解。
这篇文章针对教科书上 LDA 的目标函数抛出了三个问题，并做了相应解答，在这个过程中一步一步深入理解 LDA。
第一个问题：可不可以用均值之差而不是类间散布？
答案：可以，这样做更符合直觉，并且更容易求解。但是采用类间散布的话可以把 LDA 的目标函数表达成广义瑞利商，并且上下齐次更加合理。可能是因为这些原因，经典 LDA 最终选择了类间散布。
第二个问题：可不可以把 K 类 LDA 投影到大于 K-1 维的子空间中？
答案：不可以，因为类间散布矩阵的秩不足。K 类 LDA 只能找到 K-1 个使目标函数增大的特征值对应的特征向量，即使选择了其他特征向量，我们也无法因此受益。
第三个问题：可不可以用类间散布与类内散布的差值，而不是比值？
答案：可以，在新准则下可以得到新的最优解，但是我们无法因此受益，K 类 LDA 还是只能投影到 K-1 维空间中。差值版 LDA 与比值版 LDA 相比还缺少了一个直觉解释，可能是因为这些原因，经典 LDA 最终选择了比值。
所以，教科书版 LDA 如此经典是有原因的，它在各个方面符合了人们的直觉，本文针对它提出的三个问题都没有充分的理由驳倒它，经典果然是经典。
https://www.jiqizhixin.com/articles/2018-08-30-12
https://www.jianshu.com/p/bc97f487ad02
https://blog.csdn.net/liuweiyuxiang/article/details/78874106
https://blog.csdn.net/brucewong0516/article/details/78684005
https://www.zybuluo.com/gump88/note/402479