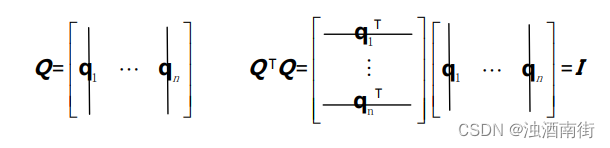
投影矩阵 P,最小二乘法,在方程无解时求“最优解”。 Gram-Schmidt 正交化——从任意一组基得到标准正交基,策略是从向量
中减去投影到其它向量方向的分量。
行列式 det(A)
三个性质定义了行列式,可以推导出之后的性质 4~10。
行列式展开公式包含 n!个非零项,一半取+,一半取-。
代数余子式公式,以及推导出逆矩阵公式
A
−
1
=
1
d
e
t
(
A
)
C
T
A^{−1}= \frac{1}{det(A)}C^T
A
−
1
=
d
e
t
(
A
)
1
C
T
特征值 Ax = λx
det(A-λI)=0
对角化:如果矩阵 A 包含 n 个线性无关的特征向量,可以对角化得到
S
−
1
A
S
=
Λ
S^{-1}AS=Λ
S
−
1
A
S
=
Λ
矩阵 A 的幂:
A
k
=
(
S
Λ
S
−
1
)
k
=
S
Λ
k
S
−
1
A^k=(SΛS^{-1})^k=SΛ^kS^{-1}
A
k
=
(
S
Λ
S
−
1
)
k
=
S
Λ
k
S
−
1
1、a =
[
2
1
2
]
\begin{bmatrix} 2\\1\\2 \end{bmatrix}
2
1
2
a)求投影到向量 a 方向的投影矩阵 P。
解:
P
=
A
(
A
T
A
)
−
1
A
T
P=A(A^TA)^{-1}A^T
P
=
A
(
A
T
A
)
−
1
A
T
,这里 a 是向量,因此有
P
=
a
a
T
a
T
a
=
1
9
[
4
2
4
2
1
2
4
2
4
]
P= \frac{aa^T}{a^Ta}=\frac{1}{9} \begin{bmatrix} 4 & 2 & 4 \\ 2 & 1 & 2 \\ 4 & 2 & 4 \end{bmatrix}
P
=
a
T
a
a
a
T
=
9
1
4
2
4
2
1
2
4
2
4
b)求矩阵 P 的秩
解:矩阵的秩为 1,因为所有的列都是第二列的倍数。或者从投影矩阵投影的空间是 1 维可以判断出来。
c)矩阵 P 的列空间?
解:向量 a 所在的直线。
d)矩阵 P 的特征值?
解:矩阵的秩为 1,因此存在重特征值 0,再从矩阵的迹可以得到另一个特征值为 1。即特征值为 1,0,0。
e)求矩阵 P 对应特征值 1 的特征向量?
解:因为矩阵 P 为投影矩阵,在投影空间中的向量就是对应特征值 1 的特征向量,因此 a 就是对应的特征向量。
f)若有
u
k
+
1
=
P
u
k
u_{k+1}=Pu_k
u
k
+
1
=
P
u
k
,且有初值 u0=
[
9
9
0
]
\begin{bmatrix} 9\\9\\0 \end{bmatrix}
9
9
0
求 uk?
解:重复将一个向量投影到一条直线,从第二次开始投影结果即不发生变化。
u
k
=
P
k
u
0
=
P
u
0
=
a
T
u
0
a
T
a
=
3
a
=
[
6
3
6
]
uk=P^ku_0=Pu_0= \frac{a^Tu_0}{a^Ta}=3a=\begin{bmatrix} 6\\3\\6 \end{bmatrix}
u
k
=
P
k
u
0
=
P
u
0
=
a
T
a
a
T
u
0
=
3
a
=
6
3
6
g)测验中可能出现
u
k
+
1
=
A
u
k
u_k+1=Au_k
u
k
+
1
=
A
u
k
,其中的矩阵 A 不是投影矩阵,没有投影矩阵的性质
P
k
u
0
=
P
u
0
P^ku_0= Pu_0
P
k
u
0
=
P
u
0
,此时需要求矩阵的特征值和特征向量。
u
0
=
c
1
x
1
+
c
2
x
2
+
c
3
x
3
u_0=c_1x_1+c_2x_2+c_3x_3
u
0
=
c
1
x
1
+
c
2
x
2
+
c
3
x
3
则
u
k
=
c
1
λ
1
k
x
1
+
c
2
λ
2
k
x
2
+
c
3
λ
3
k
x
3
uk=c_1λ_1^kx_1+c_2λ_2^k x_2+c_3λ_3^kx_3
u
k
=
c
1
λ
1
k
x
1
+
c
2
λ
2
k
x
2
+
c
3
λ
3
k
x
3
对于投影矩阵而言,
λ
1
=
1
,
λ
2
=
λ
3
=
0
λ_1=1,λ_2=λ_3=0
λ
1
=
1
,
λ
2
=
λ
3
=
0
。因此有
u
1
=
u
2
=
u
3
=
…
…
u_1=u_2=u_3=……
u
1
=
u
2
=
u
3
=
……
| t | y |
|---|---|
| 1 | 4 |
| 2 | 5 |
| 3 | 8 |
a)求利用三个数据点拟合过原点的一条直线 y=Dt?
解:
[
1
2
3
]
D
=
[
4
5
8
]
\begin{bmatrix} 1\\2\\ 3 \end{bmatrix}D=\begin{bmatrix} 4\\5\\ 8 \end{bmatrix}
1
2
3
D
=
4
5
8
,我们求解的问题就是求方程的最优解 Dˆ 。
A
T
A
D
ˆ
=
A
T
b
A^TA Dˆ =A^Tb
A
T
A
D
ˆ
=
A
T
b
。 解得 Dˆ =19/7。因此直线解析式为 y=(19/7)t。
b)怎样从投影来理解这个问题?
解:对于最小二乘问题有两种理解方法。其中一种是找到平面内最优的一条直线。另一种是将
b
=
[
4
5
8
]
b=\begin{bmatrix} 4\\5\\ 8 \end{bmatrix}
b
=
4
5
8
投影到 A 的列空间,来得到最接近于 Ax=b 的解。
向量
a
1
=
[
1
2
3
]
a_1=\begin{bmatrix} 1\\2\\ 3 \end{bmatrix}
a
1
=
1
2
3
和
a
2
=
[
1
1
1
]
a_2=\begin{bmatrix} 1\\1\\ 1 \end{bmatrix}
a
2
=
1
1
1
向量确定了一个平面,找到该平面的一组正交基。
解:应用 Gram-Shmidt 正交化方法。取 a1为第一个方向,找出垂直于该方向的向量 B。策略就是在 a2中减掉它在 a1方向上的分量,得到完全垂直于 a1的部分:
B
=
a
2
−
a
1
T
a
2
a
1
T
a
1
a
1
=
[
4
/
7
1
/
7
−
2
/
7
]
B= a_2 - \frac{a_1^Ta_2}{a_1^Ta_1}a_1 =\begin{bmatrix} 4/7\\1/7\\ -2/7 \end{bmatrix}
B
=
a
2
−
a
1
T
a
1
a
1
T
a
2
a
1
=
4/7
1/7
−
2/7
已知一个 4 阶方阵 A 具有特征值λ1,λ2,λ3,λ4。
a)特征值需要满足什么条件才能保证 A 为可逆矩阵。
解:当且仅当矩阵的特征值均不为 0 的时候,A 为可逆矩阵。若有特征值 0 存在,则矩阵零空间有非零向量,矩阵不可逆。
b)求逆矩阵行列式的值?
解:
A
−
1
A^{-1}
A
−
1
的特征值为 A 特征值的倒数。因此
d
e
t
(
A
−
1
)
=
1
λ
1
1
λ
2
1
λ
3
1
λ
4
det(A^{-1})= \frac{1}{λ_1}\frac{1}{λ_2}\frac{1}{λ_3}\frac{1}{λ_4}
d
e
t
(
A
−
1
)
=
λ
1
1
λ
2
1
λ
3
1
λ
4
1
c)求(A+I )的迹?
解:矩阵的迹等于其特征值的和,(A+I)的特征值为
λ
1
+
1
,
λ
2
+
1
,
λ
3
+
1
,
λ
4
+
1
λ_1+1,λ_2+1,λ_3+1,λ_4+1
λ
1
+
1
,
λ
2
+
1
,
λ
3
+
1
,
λ
4
+
1
,则该矩阵的迹为
λ
1
+
λ
2
+
λ
3
+
λ
4
+
4
λ_1+λ_2+λ_3+λ_4+4
λ
1
+
λ
2
+
λ
3
+
λ
4
+
4
。
已知三对角矩阵:
A
4
=
[
1
1
0
0
1
1
1
0
0
1
1
1
0
0
1
1
]
A_4=\begin{bmatrix} 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 \end{bmatrix}
A
4
=
1
1
0
0
1
1
1
0
0
1
1
1
0
0
1
1
令
D
n
=
d
e
t
(
A
n
)
D_n=det(A_n)
D
n
=
d
e
t
(
A
n
)
a)用代数余子式的方法求出
D
n
=
a
D
n
−
1
+
b
D
n
−
2
D_n=aD_{n-1}+bD_{n-2}
D
n
=
a
D
n
−
1
+
b
D
n
−
2
中的 a,b?
解:用代数余子式可得 D4=(1)D3+(-1)D2。
b)利用找到的递归方程
D
n
=
a
D
n
−
1
+
b
D
n
−
2
D_n=aD_{n-1}+bD_{n-2}
D
n
=
a
D
n
−
1
+
b
D
n
−
2
,求
D
n
D_n
D
n
?
解:把它当作方程组来求解,我们首先解得初值 D1=1,D2=0。
按照递归方程构造 2 阶线性方程:
[
D
n
D
n
−
1
]
=
[
1
−
1
1
0
]
[
D
n
−
1
D
n
−
2
]
\begin{bmatrix}D_n\\D_{n-1} \end{bmatrix} = \begin{bmatrix} 1&-1\\1&0 \end{bmatrix}\begin{bmatrix}D_{n-1}\\D_{n-2} \end{bmatrix}
[
D
n
D
n
−
1
]
=
[
1
1
−
1
0
]
[
D
n
−
1
D
n
−
2
]
求解矩阵的特征值可得:
λ
=
1
±
3
i
2
=
e
±
i
π
3
λ = \frac{1±\sqrt{3}i}{2}=\frac{e±iπ}{3}
λ
=
2
1
±
3
i
=
3
e
±
iπ
,均为模为 1 的复数,在单位圆上旋转。可以看到
λ
1
6
=
λ
2
6
=
1
λ_1^6=λ_2^6=1
λ
1
6
=
λ
2
6
=
1
,矩阵经六次变换变为单位阵。该序列既不发散也不收敛,数列以 6 次为重复周期不停循环,1,0,-1,0,1,1。
有一组对称矩阵:
A
2
=
[
0
1
1
0
]
A
3
=
[
0
1
0
1
0
2
0
2
0
]
A
4
=
[
0
1
0
0
1
0
2
0
0
2
0
3
0
0
3
0
]
A_2=\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}A_3=\begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 2 \\ 0 & 2 & 0 \end{bmatrix}A_4=\begin{bmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 2 & 0 \\ 0 & 2 & 0 & 3 \\ 0 & 0 & 3 & 0 \end{bmatrix}
A
2
=
[
0
1
1
0
]
A
3
=
0
1
0
1
0
2
0
2
0
A
4
=
0
1
0
0
1
0
2
0
0
2
0
3
0
0
3
0
a)找到投影到矩阵 A3列空间的投影矩阵 P。
解:矩阵 A3为奇异阵,其第 3 列列向量为第 1 列的 3 倍,而第 1,2 列线性无关,因此其列空间为一个平面,取其前两列列向量组成矩阵 A,则有
P
=
A
(
A
T
A
)
−
1
A
T
=
[
1
/
5
0
2
/
5
0
1
0
2
/
5
0
4
/
5
]
P=A(A^TA)^{-1}A^T=\begin{bmatrix} 1/5 & 0 & 2/5 \\ 0 & 1 & 0 \\ 2/5 & 0 & 4/5 \end{bmatrix}
P
=
A
(
A
T
A
)
−
1
A
T
=
1/5
0
2/5
0
1
0
2/5
0
4/5
可以通过将矩阵 A3的列向量乘以投影矩阵来验证这一结果,在平面内的向量投影后应该不发生变化。
b)求 A3的特征值和特征向量?
解:
d
e
t
(
A
3
−
λ
I
)
=
∣
−
λ
1
0
1
−
λ
2
0
2
−
λ
∣
=
−
λ
3
+
5
λ
=
0
det(A_3-λI)=\begin{vmatrix} -λ & 1& 0\\1& -λ& 2\\0&2&-λ \end{vmatrix} =-λ^3+5λ =0
d
e
t
(
A
3
−
λ
I
)
=
−
λ
1
0
1
−
λ
2
0
2
−
λ
=
−
λ
3
+
5
λ
=
0
解得三个特征值,λ1=0,λ2=
5
\sqrt{5}
5
,λ3=
−
5
-\sqrt{5}
−
5
。可用矩阵的迹做检查。
求解(
A
3
−
λ
I
A_3-λI
A
3
−
λ
I
)x=0,可得特征向量
x
1
=
[
−
2
0
1
]
,
x
2
=
[
1
−
5
2
]
,
x
3
=
[
1
5
2
]
x_1=\begin{bmatrix} -2\\0\\1 \end{bmatrix},x_2=\begin{bmatrix} 1\\ -\sqrt{5} \\2\end{bmatrix},x_3=\begin{bmatrix} 1\\ \sqrt{5} \\2 \end{bmatrix}
x
1
=
−
2
0
1
,
x
2
=
1
−
5
2
,
x
3
=
1
5
2
c)找到投影到矩阵 A4列空间的投影矩阵 P?
解:因为
A
4
A_4
A
4
为可逆矩阵,所以它的列空间就是整个
R
4
R_4
R
4
空间,所以 P=I。而可逆矩阵的证明可以采用求行列式的办法,用代数余子式展开可得
d
e
t
(
A
4
)
=
9
det(A_4)=9
d
e
t
(
A
4
)
=
9
。
