在这一章里,我们将探索四旋翼无人机的运动学原理。 这章将会讲机器人学中的坐标转换(Transformation)、旋转(Rotation)、欧拉角(Euler Angles)、角-轴旋转表示(Axis/Angle Representations for Rotations)、角速度(Angular Velocity) 等知识。
上一章链接:
Robotics: Aerial Robotics(空中机器人)笔记(二):无人机能量学与系统设计
坐标变换(Transformations)
在这部分中,我们将深入了解描述三维刚体运动所需的基本概念和描述三维位移的基本工具。
参考坐标系(reference frame)
首先我们来讲一下参考坐标系:
因为是要描述三维刚体运动,所以参考坐标系是三个相互正交(虽然不一定要正交,但是正交会更方便)的向量。通常对于四旋翼无人机来说,这三个方向一般如图所示,一个是无人机的前进方向,一个垂直于前进方向,最后一个是垂直于这两个轴的相交平面指向上方。


那么四旋翼无人机的速度就可以确定下来了:

刚体位移(Rigid Body Displacemen)
当这个刚体位移时,点  位移到一个新的点,我们称之为
位移到一个新的点,我们称之为 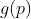 ,位移本质上是点的变换。当然如果有一个点
,位移本质上是点的变换。当然如果有一个点  ,那么位移后的点就是
,那么位移后的点就是 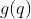 。
。 到
到  的矢量
的矢量  经过位移后的向量为
经过位移后的向量为 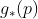 ,因为一个输入的是点,一个输入的是向量,所以名字不一样。
,因为一个输入的是点,一个输入的是向量,所以名字不一样。

那么刚体的位移有什么特性?
(1)刚体内任意两点的距离不变,这很容易理解:

(2)刚体内任意向量的外积经过位移等于位移后的向量的外积:

(3)正交的向量也互相映射:

(4)内积也满足:

旋转矩阵(Rotation Matrix):
我们在刚体位移中引入参考坐标系(向量两两正交),那么这两个参考坐标系怎么描述呢?

我们通过线性代数的学习就可以知道,每个向量都可以用相互正交的向量来描述,在三维空间中就有:

其中,这样的矩阵就是定义为旋转矩阵:

旋转矩阵的特性(Properties of a Rotation Matrix) :
(1)旋转矩阵是个正交矩阵,也就是它与它的转置相乘就是单位矩阵。
(2)其行列式等于1。
(3)任意两个旋转矩阵相乘也是旋转矩阵,也就是当刚体运动多次时,我们只需要把每个旋转矩阵相乘就能得到最后的坐标变换。
(4)旋转矩阵的逆矩阵也是旋转矩阵,这里稍微提一下,如果我们旋转一个矩阵,要把它还原回去,其实旋转回去的的旋转矩阵就是原先的逆矩阵(转回去就是逆回来)。而正交矩阵的转置是其逆矩阵,所以旋转矩阵的逆矩阵是其转置。
那么刚体位移后的点 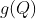 应当怎么描述?
应当怎么描述?

我们把位移后的  (称之为
(称之为 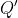 )放到位移前的参考坐标系中,那在参考坐标系下的从原点到
)放到位移前的参考坐标系中,那在参考坐标系下的从原点到 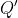
的向量可以这样描述:

其中:

旋转(Rotation)
我们之前讨论了旋转矩阵,旋转矩阵是3X3矩阵,其为正交矩阵,并且行列式的值为1。
这些类型的矩阵构成了特殊的正交群。我们用 SO(3)来指代这个群。它是指三个维度上的特殊正交
群
(Special Orthogonal group in 3 dimensions
) :

描述旋转其实有多种方法,旋转矩阵就是其中一种,但不够直观,接下来我们会讲一些描述旋转的其它方法,其中有些方法在这门课中不会提及:
(1)旋转矩阵(Rotation matrices)
(2)欧拉角(Euler angles)
(3)Axis angle parameterization
(4)指数坐标(Exponential coordinates,不讲)
(5)四元数(Quaternions,不讲)
这里还提到了一点,我们经常会使用纬度和经度来描述地球表面上的一点。也就是说这一点和这一点的经纬度是一一对应的,没有其它的点可以用这对经纬度来描述,这对经纬度也只能指代这一个点。但事实上并不是所以的点都可以由唯一的经纬度来描述,这些点就是地球的南北两极点。两极有可以一个独特的纬度,但经度却没有明确定义。事实上,任何经度都可以用来描述北极或南极。

为什么特别提出这一点呢?这在后面的内容会有涉及。
欧拉角(Euler Angles)
欧拉证明了描述一般旋转需要三个坐标,这些坐标称为欧拉角。如果我们要描述A坐标系到D坐标系的旋转 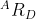 ,我们可以将其分解成三个过程,分别是将A坐标系绕
,我们可以将其分解成三个过程,分别是将A坐标系绕  轴旋转角度
轴旋转角度 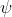 ,绕
,绕  轴旋转角度
轴旋转角度 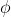 以及绕
以及绕  轴旋转角度
轴旋转角度  ,其中这三个角度就是翻滚角(roll)、俯仰角(pitch)和偏航角(yaw),并且这样的描述方式我们称之为X-Y-Z 欧拉角:
,其中这三个角度就是翻滚角(roll)、俯仰角(pitch)和偏航角(yaw),并且这样的描述方式我们称之为X-Y-Z 欧拉角:

还有一种描述方式我们称之为Z-Y-Z欧拉角,其实就是先绕  轴旋转
轴旋转 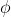 ,再绕
,再绕  轴旋转
轴旋转  ,最后再绕
,最后再绕  轴旋转
轴旋转 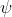 :
:

我们发现当  不为 0 时,其它两个旋转时的
不为 0 时,其它两个旋转时的  轴是不共线的,这三个旋转的组合就可以与特定的旋转一一对应。但当
轴是不共线的,这三个旋转的组合就可以与特定的旋转一一对应。但当  为 0 时, 其它两个旋转时的
为 0 时, 其它两个旋转时的  轴是共线的,这时候的情况就与地球的南北两极点类似。比如说,当
轴是共线的,这时候的情况就与地球的南北两极点类似。比如说,当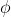 =
= 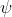 = 45度时实际步就是绕
= 45度时实际步就是绕  轴旋转了90度,那么其实也可以用
轴旋转了90度,那么其实也可以用 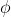 = 30度且
= 30度且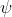 = 60度来描述,也就是说这个旋转组合的描述就不唯一了。
= 60度来描述,也就是说这个旋转组合的描述就不唯一了。

我们再深入了解一下,Z-Y-Z欧拉角对应的旋转矩阵如下:

怎么推的,这里我用matlab代码演示一下:
syms psi theta phi real; %定义三个角度的符号变量并设置成实数
R1 = [cos(phi) -sin(phi) 0; sin(phi) cos(phi) 0; 0 0 1];
R2 = [cos(theta) 0 sin(theta); 0 1 0; -sin(theta) 0 cos(theta)];
R3 = [cos(psi) -sin(psi) 0; sin(psi) cos(psi) 0; 0 0 1];
simplify(R1*R2*R3)
结果就是上面的公式,至于R1,R2,R3为什么这么设置,推荐看下面的链接:
3维旋转矩阵推导与助记
感兴趣的同学也可以试下用代码看一下X-Y-Z欧拉角的旋转矩阵的样子。
假如我们已经知道了旋转矩阵的具体值,那么通过绿色的方框也就是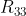 我们就能求得
我们就能求得  的值,再通过蓝色的方框我们就能求得
的值,再通过蓝色的方框我们就能求得 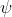 的值,同时通过黄色的方框求得
的值,同时通过黄色的方框求得 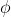 的值:当
的值:当 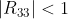 时的计算公式如下:
时的计算公式如下:

注意这里用的是atan2函数。这是因为如果用普通的反正切,输入正切值的话会造成模糊的结果,用atan2函数则可以避免:


当 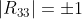 时,我们会发现,旋转矩阵里的每一个元素其实都是关于
时,我们会发现,旋转矩阵里的每一个元素其实都是关于 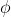 和
和 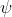 的正余弦角度求和公式,所以说这时的旋转矩阵其实就是一个关于
的正余弦角度求和公式,所以说这时的旋转矩阵其实就是一个关于 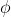 +
+ 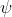 的函数。假设
的函数。假设 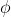 +
+ 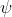 =90,那么就有无数个
=90,那么就有无数个 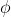 和
和 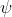 的组合满足这一条件。就如同我们之前讲的Z-Y-Z欧拉角中绕
的组合满足这一条件。就如同我们之前讲的Z-Y-Z欧拉角中绕  轴旋转的
轴旋转的  为 0 时, 其它两个旋转时的
为 0 时, 其它两个旋转时的  轴是共线的,那这个旋转组合的描述就不唯一了。
轴是共线的,那这个旋转组合的描述就不唯一了。

最后还讲到他们实验室用的四旋翼无人机常用的欧拉角描述方式是 Z-X-Y欧拉角,如下图所示:

角-轴旋转表示(Axis/Angle Representations for Rotations)
现在看看另一种描述旋转的方式,这种方式给定一个旋转轴和旋转角度就能描述一个旋转。
假设刚体上有一个点O,如果经过位移后这个点O保持不变,就相当于刚体在绕着这个穿过点O的轴旋转。
怎么证明这一点呢?
通过之前的讨论我们可以知道,刚体经过旋转后的某个点可以这样表示:

所以我们就有两个3 X 1的向量 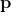 和
和 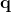 ,与旋转矩阵相关:
,与旋转矩阵相关:

那么我们想知道的是:是否存在一个点 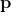 使得经过 R 的旋转后,保持不变?也就是:
使得经过 R 的旋转后,保持不变?也就是:

这个形式学过线性代数的同学就会很熟悉,这不就是特征向量和特征值吗:

所以当特征值,也就是 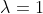 里就是这个问题的解,也就是说结果是存在的,即经过旋转后p的方向和大小保持不变,那就相当于绕着经过
里就是这个问题的解,也就是说结果是存在的,即经过旋转后p的方向和大小保持不变,那就相当于绕着经过 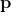 的轴旋转了。
的轴旋转了。
接下来我们反过来思考,给定一个特定的轴 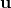 和旋转方向
和旋转方向 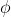 ,我们怎么计算旋转矩阵?如下图所示,我们建立一个与旋转轴
,我们怎么计算旋转矩阵?如下图所示,我们建立一个与旋转轴 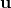 垂直的向量
垂直的向量 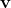 ,把
,把 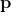 分解成这两个向量的量,那么在
分解成这两个向量的量,那么在 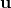 方向上的分量就是
方向上的分量就是 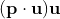 (因为点积就是求一个向量在另一个方向的投影的大小)。在
(因为点积就是求一个向量在另一个方向的投影的大小)。在 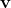 方向上的分量就是
方向上的分量就是 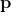 本身减去
本身减去 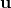 方向上的分量
方向上的分量 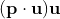 ,由于是在三维空间,我们还建了一个
,由于是在三维空间,我们还建了一个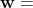
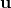 X
X 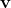 的轴,表示与其它两个轴正交:
的轴,表示与其它两个轴正交:

接下来我们可以考虑绕特定的轴 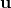 和旋转
和旋转 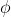 的情况了,其相关的公式如下图所示,我们来进行一个个推导:
的情况了,其相关的公式如下图所示,我们来进行一个个推导:

首先是向量 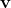 绕
绕 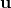 旋转后的向量,我们可以用其在
旋转后的向量,我们可以用其在 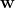 和
和 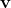 上的分量相加得到,也就是:
上的分量相加得到,也就是:

那么向量 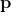 在这个向量上的投影就是把
在这个向量上的投影就是把 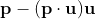 代入到
代入到 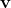 :
:

由于向量 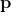 在
在 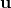 轴上的分量
轴上的分量 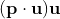 旋转后也不会变化,所以向量
旋转后也不会变化,所以向量 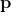 旋转后的向量就是这两个向量相加:
旋转后的向量就是这两个向量相加:

 其中
其中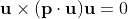
我们把 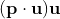 改写成向量相乘的形式:
改写成向量相乘的形式:
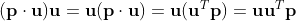
那么就得到:

因为叉积的形式可以这么表达,我们用hat操作符表示一个反对称矩阵:

所以就有:
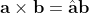
所以就得到最终的形式以及相应的旋转矩阵:


通过这个旋转矩阵的公式我们就可以知道,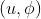 和
和 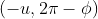 可以描述同一个旋转,所以不是一对一的关系,那么要是把
可以描述同一个旋转,所以不是一对一的关系,那么要是把 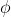 限制到
限制到 ![[0,\pi]](https://latex.codecogs.com/gif.latex?%5B0%2C%5Cpi%5D) 呢,这个我们后面讨论。
呢,这个我们后面讨论。

得到这个旋转矩阵之后,我们怎么求得对应的轴 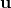 和旋转角度
和旋转角度 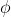 呢?公式如下:
呢?公式如下:

其中 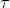 是旋转矩阵的迹:
是旋转矩阵的迹:



由于反对称矩阵的性质我们可以知道 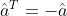 ,而旋转矩阵的转置其它两个相加的量不会发生变化,所以我们就有:
,而旋转矩阵的转置其它两个相加的量不会发生变化,所以我们就有:
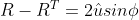
所以得证。由公式就可以知道当 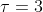 时
时 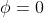 ,那么相当于没有旋转,也就不用讨论要绕那个特定的轴,换句话说,就是任意的轴都可以用来描述。也就是此时
,那么相当于没有旋转,也就不用讨论要绕那个特定的轴,换句话说,就是任意的轴都可以用来描述。也就是此时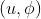 和旋转矩阵不是一对一的关系。
和旋转矩阵不是一对一的关系。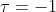 时
时 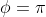 ,可以用
,可以用 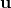 和
和 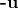 来描述,我们可以把其代入公式看看,所以也不是一对一的关系。所以当把
来描述,我们可以把其代入公式看看,所以也不是一对一的关系。所以当把 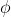 限制到
限制到 ![[0,\pi]](https://latex.codecogs.com/gif.latex?%5B0%2C%5Cpi%5D) 时,除了这两种情况其它都是一对一的关系。
时,除了这两种情况其它都是一对一的关系。

角速度(Angular Velocity)
讨论完旋转的概念之后,我们就可以来讲一下旋转变化率,也就是角速度了。我们知道,线速度的话就是位移对时间求导,那么自然地,求角速度就是旋转角度对时间求导。
现在我们来对一个3 X 3 的旋转矩阵求导,我们知道,旋转矩阵是正交的,所以有如下性质,并对其求导得到如下的恒等式:

那么我们就可以得到 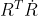 和
和 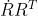 是反对称矩阵,简单推导
是反对称矩阵,简单推导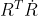 ,另一个同理:
,另一个同理:
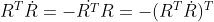
我们再来考虑如下的旋转:

这次我们要想象,这次的旋转是随着时间发生变化的,也就是:

注意到向量 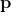 是一个常量,因为我们把
是一个常量,因为我们把 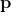 放在固连系(body-fixed frame)思考,也就是这个坐标系会随着刚体的旋转而旋转,即
放在固连系(body-fixed frame)思考,也就是这个坐标系会随着刚体的旋转而旋转,即 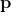 在这个坐标系上的位置不会发生改变,而q是在惯性系(inertial frame)考量的,也就是有一个绝对的坐标系,它不会随着刚体的旋转而发生改变。所以有以上的式子。
在这个坐标系上的位置不会发生改变,而q是在惯性系(inertial frame)考量的,也就是有一个绝对的坐标系,它不会随着刚体的旋转而发生改变。所以有以上的式子。
我们对这个式子求导,所以左边的部分的 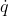 是惯性系下的速度,右边部分的
是惯性系下的速度,右边部分的  是固连系下的位置:
是固连系下的位置:

然后我们在式子两边同时左乘上 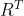 ,那么在式子右边就是固连系下的速度。这是因为我们在上面两个坐标系的定义就可以知道,固连系旋转回去就和惯性系重合,就得到如下的式子,紫色方框内的变量我们在上面就推导出了是反对称矩阵,所以可以用
,那么在式子右边就是固连系下的速度。这是因为我们在上面两个坐标系的定义就可以知道,固连系旋转回去就和惯性系重合,就得到如下的式子,紫色方框内的变量我们在上面就推导出了是反对称矩阵,所以可以用 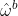 表示:
表示:

那在惯性系下的表示如下,用 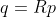 两式左乘
两式左乘 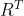 得到
得到 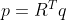 ,将其代入上式中得到。同理橙色方框的式子用
,将其代入上式中得到。同理橙色方框的式子用 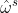 表示:
表示:

有了这两个式子,我们就可以分别求到惯性系和固连系上的角速度。
下一章链接:
Robotics: Aerial Robotics(空中机器人)笔记(四):无人机动力学
本文内容由网友自发贡献,版权归原作者所有,本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容,请联系:hwhale#tublm.com(使用前将#替换为@)