基于拉格朗日对偶的凸全局三维配准

2023-05-16

在这里插入图片描述
论文地址

文章导读

最近自己的工作有借鉴这篇文章中用到的拉格朗日对偶，然后就细读了文章的内容并且分析了对应的代码。拉格朗日对偶属于凸优化的范畴，详细的定义和理论可以在《Convex optimization》一书中进行深入学习。本篇博客仅重点解读该文章的主要内容。

摘要

通过欧几里德变换进行三维模型的配准是计算机视觉中许多核心应用的基础任务。因为旋转约束，所以这个问题是非凸的，这就使得传统的局部优化方法容易陷入局部极小值。本文集成常见的几何配准模态（比如点对点，点对线，点对平面），建立一个统一的公式，从而在多个三维配准问题中寻找全局最优变换。这个公式使得优化问题与对应关系的数量和性质无关。
本工作的主要创新点是引入该问题的强化拉格朗日对偶松弛，这个松弛在有效性上超越了之前类似的方法[1]。事实上，虽然没有理论上的保证，但在合成和真实数据实验中进行的经验上详尽的验证，通常能够产生紧的松弛，这样就可以利用对偶理论，恢复一个能够保证的全局最优解。
因此，该方法允许在全局最优性能够保证的前提下有效地求解三维配准问题，并且，该方法比基于计算量更大的Branch and Bound的当前最先进方法[2]运行速度更快。

动机

将多模态（基于）配准问题统一到一个框架中；
能够全局地求解三维多模态配准问题，不需要依赖初始值；
能够比基于搜索求解的方法运行得更快；
能够提供正式的性能保证，也就是全局最优性保证。

主要贡献

将点对点、点对线和点对平面的对应关系整合为一个二次目标的统一公式，该二次目标是只关于旋转矩阵的函数；
针对该统一的公式，在拉格朗日对偶问题的一般框架下设计全新的凸松弛，从而产生一个小规模的半定规划问题（SDP）。

算法流程

多模态配准
1.1 三维配准原生问题
给定物体的三维点集 { x i } i = 1 m \left \{ x_i \right \}^m_{i=1} {xi}i=1m 和对应模型的三位基元（一般是点，线或者平面） { P i } i = 1 m \left \{ P_i \right \}^m_{i=1} {Pi}i=1m，以及它们之间的对应关系 x i ↔ P i x_i \leftrightarrow P_i xi↔Pi，则原生的三维配准问题就是寻找一个包含旋转和平移的变换 T = ( R , t ) ∈ S E ( 3 ) T=(R, t) \in SE(3) T=(R,t)∈SE(3) 满足：

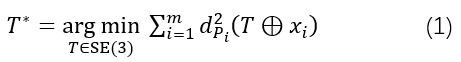
1.2 广义距离函数
三维点 x x x 到三维基元 P P P 的平方距离可以表示为一个广义距离函数：

其中 y y y 为 P P P 上的任意一点， C C C 是一个对称矩阵，根据不同的基元，会有不同的形式，如下图所示

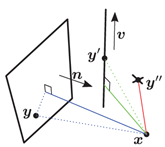
因为基元 P P P 可以有三种情况，分别是点，直线和平面，那么实际上广义距离函数（1）也可以根据这三种基于写成三种形式：
点：

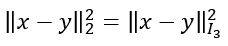
直线：

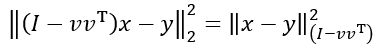
v v v 为直线的单位方向向量
平面：

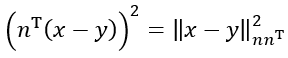
n i n_i ni 是平面的单位法向量
1.3 二次模型
首先将变换矩阵 T T T 拆开表示为旋转 R R R 和平移 t t t，这样就可以得到如下线性的参数化：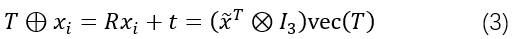
其中， x ~ = [ x T , 1 ] T \tilde{x} = [x^T,1]^T x~=[xT,1]T 是 x x x 的齐次形式， ⊗ \otimes ⊗ 是克罗内克积， v e c ( T ) vec(T) vec(T) 是变换矩阵的向量化。这样， T ⊗ x i T \otimes x_i T⊗xi 对于 R R R 和 t t t 是线性的。
然后根据广义距离定义(2)，三维配准原生问题中的距离可以表示为 τ = v e c t ( T ) \tau=vect(T) τ=vect(T) 的二次函数：

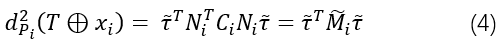
其中 N i = [ x ~ i T ⊗ I 3 ∣ − y i ] N_i=[\tilde{x}^T_i \otimes I_3 | -y_i] Ni=[x~iT⊗I3∣−yi]， τ ~ = [ v e c ( T ) T , 1 ] \tilde{\tau}=[vec(T)^T,1] τ~=[vec(T)T,1]。
将所有测量值 x i x_i xi 和 y i y_i yi 累积起来组成一个13维的矩阵 M ~ \tilde{M} M~，则整体的目标函数为：

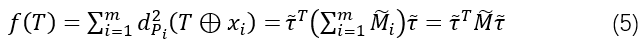
1.4 边缘化的二次模型
通过边缘化平移量 t t t，目标函数(5)可以进一步约化为：

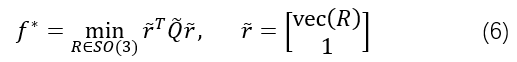
然后通过(6)中得到的 r ~ \tilde{r} r~，求解一个线性系统就可以直接得到最优的平移：

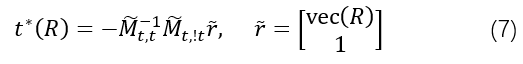
其中下标 t t t 表示对应于平移变量的索引， ! t !t !t 表示 t t t 的补， Q ~ = M ~ / M ~ t , t \tilde{Q}=\tilde{M}/\tilde{M}_{t,t} Q~=M~/M~t,t 是矩阵 M ~ \tilde{M} M~ 中矩阵块 M ~ t , t \tilde{M}_{t,t} M~t,t 的舒尔补。
边缘化问题的紧对偶松弛
边缘化问题(6)对于旋转 R 仍然是一个非凸问题，所以这里采用一个凸松弛求解该问题
2.1 原问题
为了应用拉格朗日对偶松弛，首先将问题(6)转化为一个QCQP问题，因为(6)中目标函数已经是一个二次型了，所以接下来的工作就是将(6)中可行域参数化为尽可能多的二次约束。
对于旋转矩阵的正交约束，文献[3]针对列正交和行正交，提供了一组完整的二次约束：

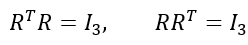
文献[4]提出旋转矩阵的列需要满足右手定则，才能保证旋转矩阵的行列式为+1，比如：

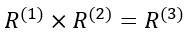
其中， R ( k ) R^{(k)} R(k) 是旋转矩阵 R R R 的第k列。
同时引入辅助变量 y y y，增加额外约束 y 2 = 1 y^2=1 y2=1，问题（6）就可以重新建模为一个等价、齐次、加强的原问题：

2.2 对偶问题
原问题( P ~ \tilde{P} P~)是一个QCQP问题，它的拉格朗日函数为：

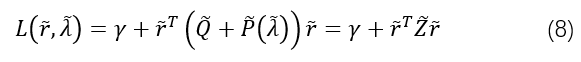
其中，齐次对偶向量为 λ ~ = [ λ T , γ ] T ∈ R 22 \tilde{\lambda}=[\lambda^T, \gamma]^T \in \mathbb{R}^{22} λ~=[λT,γ]T∈R22，对偶变量 λ \lambda λ 对应于所有的旋转矩阵约束， γ \gamma γ 对应于齐次约束 y 2 = 1 y^2=1 y2=1，如下图所示； Q ~ \tilde{Q} Q~ 包含原问题的所有数据， P ~ ( λ ~ ) = P ~ r ( Λ r ) + P ~ c ( Λ c ) + P ~ d ( { λ d i j k } ) + P ~ h ( γ ) \tilde{P}(\tilde{\lambda})=\tilde{P}_r(\Lambda_r)+\tilde{P}_c(\Lambda_c)+\tilde{P}_d(\left\{ \lambda_{d_{ijk}} \right\})+\tilde{P}_h(\gamma) P~(λ~)=P~r(Λr)+P~c(Λc)+P~d({λdijk})+P~h(γ) 表示对应于不同约束的所有惩罚项的和，它们组成了惩罚矩阵 Z ~ \tilde{Z} Z~。

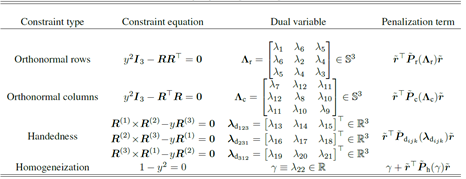
所以拉格朗日对偶函数为：

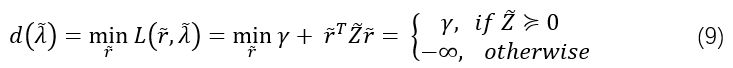
那么对应于原问题( P ~ \tilde{P} P~)的对偶问题就是是一个半正定规划(SDP)：

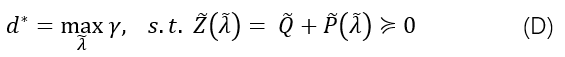
这个问题就是凸的，并且很容易用现有的算子求解。
2.3 通过对偶解求原问题
根据对偶理论，原问题最优解 r ~ ∗ \tilde{r}^* r~∗ 必须是拉格朗日函数（8）在 λ ~ ∗ \tilde{\lambda}^* λ~∗ 处最小值的解：

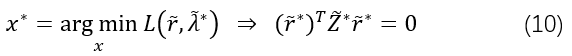
因为 Z ~ ⪰ 0 \tilde{Z} \succeq 0 Z~⪰0，所以原问题最优解 r ~ ∗ \tilde{r}^* r~∗ 属于 Z ~ ∗ \tilde{Z}^* Z~∗ 的零空间：
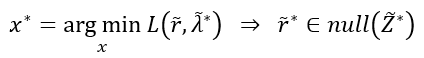
问题整体算法
多模态配准问题的整体算法如下：

其中边缘化问题(6)的算法(Alg. 2)如下：

算法主要代码解析

该算法的主要部分为函数 function [R,t,dstar,times,R0] = method_RCQP( correspondences, header )

公式(5)将所有测量值 x i x_i xi 和 y i y_i yi 对应点累积起来组成一个13维的矩阵 M ~ \tilde{M} M~

function q = compress_quadData( correspondences )
  % q = compress_quadData( correspondences )
  % Given correspondences whose cost function is quadratic in the unknowns,
  % compress the problem data into a single quadratic function.
 % Initialize quadratic form
  q = Quadratic(zeros(13));
  % Accumulate quadratic form corresponding to each correspondence
  for i=1:numel(correspondences)
  q = q + quad( correspondences(i) );
  end
end

公式(6)边缘化

function [q_margin, A] = marginalize(q,i)
  % [q_margin, A] = marginalize(q,MARGINALIZED_IDXS)
  % Compute the marginalization of a quadratic form
  % wrt the variables y in positions MARGINALIZED_IDXS.
  % This consists of finding the critical point wrt those variables,
  % find the optimal value in terms of the rest of unknowns as
  %   y_optim = A*x
  % and obtain the quadratic form q(x) wrt the remaining variables x.
  %
  % The results here are obtained from directly deriving the quadratic
  % function (simpler if homogeneized) wrt the desired variables.
  % The results are equivalent to applying the Schur complement.
      
  % Get matrix data
  M = q.Q_;
  dim = size(M,1);
  not_i = setdiff(1:dim,i);
      
  % Compute marginalized cost function (a new quadratic form)
  M_margin = M(not_i,not_i) - M(not_i,i)*pinv(M(i,i))*M(i,not_i);
  q_margin = Quadratic(symmetrize(M_margin));
      
  if nargout == 2
    % Compute linear map from non-marginalized x to marginalized y
    s = svd(M(i,i));
    if s(end) < 1e-2
      warning('Marginalization possibly degenerate: sv(end)=%E',s(end))
    end
    A = -pinv(M(i,i))*M(i,not_i);
  end
end

求解对偶SDP问题(D)为函数function [d,Z,G,lam,time] = solve_dual_template( q, header )
a) 构建对偶变量 λ ~ = [ λ T , γ ] T \tilde{\lambda}=[\lambda^T, \gamma]^T λ~=[λT,γ]T

lam = Clam_RCQP( lam_unit_cols, lam_unit_rows,...
                 		   lam_ort_cols, lam_ort_rows,...
                      	   lam_det, lam_g );

b) 根据对偶变量计算各个惩罚项

function Qpen_ = build_penalizationMat( lam )
% Qpen_ = build_penalizationMat( lam )
% 
% Creates the *homogeneous* penalization matrix for LMI in SDP:
%   Z = Q0_ + Qpen_(lam) >= 0
% 
% The penalization matrix depends *only* on the dual variables lam
% It is independent of the problem data or the primal variables
% 
% The expressions are mat-like (more compact), see the report for details 
 
% Assert the values of lam are given struct-like
if numel(lam)==22 || ~isstruct(lam) && ~isobject(lam)
  % Convert from vec-format to struct-format
  lam = Clam_RCQP(lam);
end
 
% Quadratic term
Lam_cols = diag(lam.unit_cols) + 0.5*offsym(lam.ort_cols);
Lam_rows = diag(lam.unit_rows) + 0.5*offsym(lam.ort_rows);
skew_det = cell(1,3);
for k=1:3
  skew_det{k} = skew(lam.det(:,k));
end
Q_pen = -kron(Lam_cols,eye(3)) - kron(eye(3),Lam_rows) + 0.5*skew( skew_det );
 
% Linear term
b_pen = - 0.5*vec(lam.det);
 
% Independent term
c_pen = sum(lam.unit_cols) + sum(lam.unit_rows) - lam.g;
 
% Complete homogeneous matrix
Qpen_ = [Q_pen  b_pen;
         b_pen' c_pen];
 
end

c) 计算惩罚矩阵

% Build slack matrix: -P + Z = Q ? Z = Q + P
% Penalize homogeneous quadratic matrix (PSD slack matrix)
if all(size(q.Q_)==[10 10])
  % Marginalized case: [vec(R) y]
  Z = q.Q_ + P;
elseif all(size(q.Q_)==[13 13])
  % Non-marginalized case: [vec(R) t y]
  % Pad with zero blocks in penalization
  P_padded = [ P(1:9,1:9) zeros(9,3) P(1:9,end)
               zeros(3,9) zeros(3,3) zeros(3,1)
               P(end,1:9) zeros(1,3) P(end,end) ];
    Z = q.Q_ + P_padded;
else
  error('Wrong dimensions of the quadratic function')
end

d) 设置SDP目标函数和约束函数

Z = symmetrize(Z);
dual variable G
G : Z >= 0; % Slack matrix must be positive semidefinite
d = lam_g;
maximize(d)

通过对偶解求原问题的最优旋转和平移
(a) 零空间求解原问题的初步解

function [R,szep] = solve_PrimalFromDual( Z )
% [R,szep] = solve_PrimalFromDual( Z )
 
% Decompose penalized matrix
[U,S,~] = svd(full(Z));
s = diag(S);
 
% Check SZEP condition,
szep = s(end)<1e-3 && (s(end)/s(end-1))<1e-3;
% Zero eigenvalue and margin to distinguish from numerical accuracy
 
if szep
  % Recovering the solution is trivial, just scale the eigenvector
  r = makenonhom( U(:,end) );
  R = reshape(r,3,3);
else
  error('No solution for non-tight case through nullspace yet')
end
 
end

(b) 将初步解投影到SO(3)流形上，得到最近似的最优旋转矩阵

function [R,f] = project_rotation( M, fmin )
% R = project_rotation( M )
% 
% Takes a general linear matrix M and projects it to
% the rotation matrix in SO(3) minimizing the chordal distance.
% This is equivalent to find the closest matrix under Frobenius norm
% (see "Hartley et al. Rotation averaging" in IJCV).
% 
% The problem is solved using the SVD decomposition of M:
%   M = U*S*V'
% If det(U*V')>0, R = U*V'
% BUT if det(U*V')<0, R = U*V'
% 
% 
% [R,f] = project_rotation( M, fmin )
% If the projected rotation seeks to minimize a certain objective fmin,
% it may be preferrable to search for the rotation
%   R=U*S*V', S=diag(s_i), s_i=+-1
% that minimizes fmin (this can be done by brute-force search)
 
% Project to valid rotation
[U,D,V] = svd(M);
if nargin == 1
  if det(U*V')>0
    R = U*V';
  else
    R = U*diag([1 1 -1])*V';
  end
else
  if det(U*V')>0
    signs = {[1 1 1],[1 -1 -1],[-1 1 -1],[-1 -1 1]};
  else
    signs = {[-1 1 1],[1 -1 1],[1 1 -1],[-1 -1 -1]};
  end
  numCombs = numel(signs);
  fvalues = zeros(1,numCombs);
  for i=1:numCombs
    fvalues(i) = fmin(U*diag(signs{i})*V');
  end
  [f,bestIdx] = min(fvalues);
  R = U*diag(signs{bestIdx})*V';
end

t = A*makehom(vec(R0));

主要实验结果

对比方法：一个BnB方法[2]，Olsson[1]方法，该方法
度量尺度：次最优间隙，最优率，算法耗时
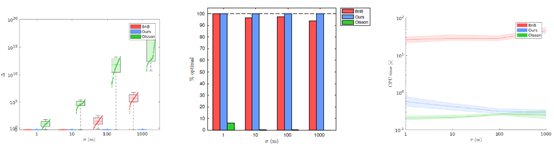
生成数据比较结果
3.1 噪声变化，测量对应点数量不变

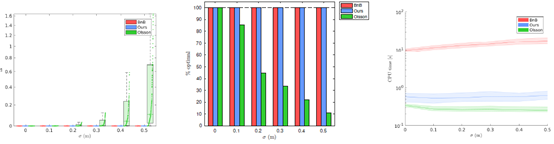
3.2 测量对应点数量变化，噪声不变

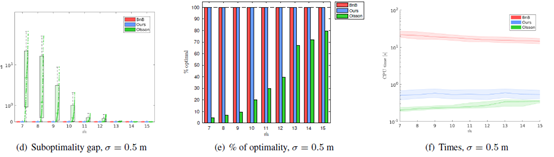
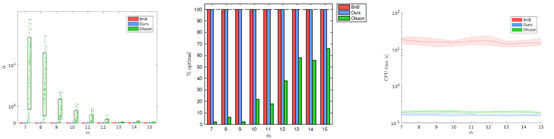
3.3 极端实验：测量对应点数量最小为7，噪声很大
真实数据(来自文献[1])比较结果

总结

这个工作提出了一个基于拉格朗日对偶理论的算法，用于解决广义的三维配准问题。虽然该方法通过大量实验证实经验上全局最优，但也是存在问题和改进点的：

算法本身还是基于SDP的，而且使用现有的原生SDP算子，所以可能会有随着问题规模增大求解速度大幅变慢的问题，所以可以利用底层SDP问题的低秩结构设计专门的算子
作者在文章中也说明了这个工作里的全局性能并没有理论上的证明，只是经验上(也就是大量实验结论)的全局最优保证，所以可以从理论上去分析紧度和证明最优性

该工作的作者有一系列使用对偶(优化)理论的solid工作，十分值得学习和研究。

参考文献

[1] C. Olsson and A. Eriksson. Solving quadratically constrained geometrical problems using lagrangian duality. In Pattern Recognition, 2008. ICPR 2008. 19th Int. Conf., pages 1–5. IEEE, 2008.
[2] C. Olsson, F. Kahl, and M. Oskarsson. Branch-and-Bound Methods for Euclidean Registration Problems. IEEE Trans. Pattern Anal. Mach. Intell., 31(5):783–794, 2009.
[3] K. Anstreicher and H.Wolkowicz. On Lagrangian relaxation of quadratic matrix constraints. SIAM J. Matrix Anal. Appl., 22(1):41–55, 2000.
[4] R. Tron, D. M. Rosen, and L. Carlone. On the Inclusion of Determinant Constraints in Lagrangian Duality for 3D SLAM.

本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容，请联系:hwhale#tublm.com(使用前将#替换为@)