几年前就想写这篇文章，但是在解析神经网络的数学原理问题上断断续续，加上个人能力有限，很多问题并没有研究的很明白，以及神经网络本身高维问题的复杂性，导致这个问题的理解也是有限的。个人希望在这篇文章里抛砖引玉，让大家能更深入理解神经网络内部的基础数学原理与编码逻辑，启发大家后面的工作，如有错误请不吝啬指出。本文不会过多的介绍梯度下降或反向传播等参数更新的原理或动力学过程，而是以前向过程（Feed Forward）作为本文的重点。
和支持向量机（Support Vector Machine）一样，在神经网络或深度学习中也几乎处处都会涉及到分离超平面，也是其核心内容之一，所以这里会用较大的篇幅说明分离超平面的内容。
分离超平面（Separating Hyperplane）是指将两个不相交的凸集分割成两部分的一个平面。在数学中，超平面是 n n n 维欧氏空间中余维度等于 1 的线性子空间 。 H = { x ∣ w T x + b = 0 } H=\{x \mid w^Tx+b = 0\} H={x∣wTx+b=0} 就是这样的一个分离超平面，即将 n n n维欧式空间分离为两个半空间的一个超平面。
对于只有1个变量的方程 w 1 x 1 + b = 0 w_1x_1+b=0 w1x1+b=0而言，能显然得到 x 1 = − b w 1 x_1=\frac{-b}{w_1} x1=w1−b，在 1 1 1维直线上 x x x为一个点，将直线分为两部分。
而对于有2个变量的方程 w 1 x 1 + w 2 x 2 + b = 0 w_1x_1+w_2x_2+b=0 w1x1+w2x2+b=0我们能直接计算出 x 2 = ( − w 1 x 1 − b ) / w 2 x_2=(-w_1x_1-b)/w_2 x2=(−w1x1−b)/w2，我们做一次代数替换 α = − w 1 w 2 ， β = − b w 2 \alpha=\frac{-w_1}{w_2}，\beta=\frac{-b}{w_2} α=w2−w1，β=w2−b，方程变为了 x 2 = α x 1 + β x_2=\alpha x_1+\beta x2=αx1+β，这个是一元一次函数的等价形式，其中 α \alpha α为斜率 β \beta β为截距，当 α , β \alpha,\beta α,β确定时，该函数在2维平面是一条直线，将平面一分为二。
当方程为3个变量是时， w 1 x 1 + w 2 x 2 + w 3 x 3 + b = 0 ⇔ x 3 = α x 1 + β x 2 + γ w_1x_1+w_2x_2+w_3x_3+b=0\Leftrightarrow x_3 =\alpha x_1+\beta x_2+\gamma w1x1+w2x2+w3x3+b=0⇔x3=αx1+βx2+γ ，该函数在三维空间中是一个平面，将三维空间分离为2个子空间。
同理 n > 3 n>3 n>3时， H = { x ∣ w T x + b = 0 } H=\{x \mid w^Tx+b = 0\} H={x∣wTx+b=0} 是 n n n维空间中的一个超平面，由于物理限制我们无法直观的画出超平面了，但是这个超平面是存在的，所谓分离超平面只是沿用 3 3 3维空间中分离平面的概念。为了方便，在任意维的空间中我们统一称 H = { x ∣ w T x + b = 0 } H=\{x \mid w^Tx+b = 0\} H={x∣wTx+b=0}为分离超平面，或简称 w T x + b = 0 w^Tx+b=0 wTx+b=0为分离超平面，在超平面的一侧 w T x + b > 0 w^Tx+b>0 wTx+b>0，在超平面的另一侧 w T x + b < 0 w^Tx+b<0 wTx+b<0。
我们知道感知机 (perceptron) 是一个线性分类模型，其公式如下：
y
=
s
i
g
n
(
w
T
x
+
b
)
=
{
1
,
w
T
x
+
b
>
0
−
1
,
w
T
x
+
b
⩽
0
y = sign(w^Tx+b) =\left\{\begin{matrix} 1&,w^Tx+b>0 \\ -1&,w^Tx+b\leqslant 0 \end{matrix}\right.
y=sign(wTx+b)={1−1,wTx+b>0,wTx+b⩽0单层感知机是非常简单的一个模型，激活函数
s
i
g
n
(
x
)
sign(x)
sign(x)将超平面的一侧的输入空间强制划分为
1
1
1，另一侧划分为
−
1
-1
−1，本质上是分离超平面的推广（当然激活函数也是神经网络中的核心内容之一，后文会详细解释），为了能使用随机梯度下降(SGD)等算法，即函数可微，我们可以将
s
i
g
n
(
x
)
sign(x)
sign(x)函数替换为
t
a
n
h
(
x
)
tanh(x)
tanh(x)、
s
i
g
m
o
i
d
(
x
)
sigmoid(x)
sigmoid(x)或
R
e
L
U
(
x
)
ReLU(x)
ReLU(x)。因为感知机非常简单，这里只简单介绍，我们的重点放在不含隐藏层的全连接（Fully Connected，FC）模型解析上。
单层线性回归模型 y = w T x + b y=w^Tx+b y=wTx+b，区别于分类模型，回归模型相当于直接求超平面，而不必硬性划分超平面的两侧，所以回归和分类一脉相承，核心内容是一样的，这也是神经网络可以既用来做分类也可以用来做回归的原因。区别之处在回归的 y y y值是连续的，而分类是离散的。后文会讲到如何将分类问题转换为回归问题。
读者可能会疑问，感知机不就是二分类的单层全连接模型吗？是的，我们知道在神经网络中一般有多少个分类就有多少个输出节点，对于神经网络的二分类而言我们一般使用2个节点作为输出，最后我们会阐明感知机模型等价于单层全连接二分类模型。 研究2个节点的原理能更好理解多节点的情形。
对于输出节点1，我们有
y
1
=
w
1
T
x
+
b
1
y_1 = w^T_1x+b_1
y1=w1Tx+b1，对于输出节点2，我们有
y
2
=
w
2
T
x
+
b
2
y_2 = w^T_2x+b_2
y2=w2Tx+b2，在全连接分类模型中我们一般使用
a
r
g
max
(
x
)
arg \max(x)
argmax(x)获得输出节点的分类标签，即：
y
=
a
r
g
max
(
y
1
,
y
2
)
=
{
1
,
w
1
T
x
+
b
1
≥
w
2
T
x
+
b
2
2
,
w
1
T
x
+
b
1
<
w
2
T
x
+
b
2
y = arg \max(y_1,y_2)=\left\{\begin{matrix} 1&,w^T_1x+b_1\geq w^T_2x+b_2 \\ 2&,w^T_1x+b_1<w^T_2x+b_2 \end{matrix}\right.
y=argmax(y1,y2)={12,w1Tx+b1≥w2Tx+b2,w1Tx+b1<w2Tx+b2在上式中我们注意到，该二分类模型的决策超平面为
w
1
T
x
+
b
1
=
w
2
T
x
+
b
2
w^T_1x+b_1 = w^T_2x+b_2
w1Tx+b1=w2Tx+b2，这里我们作一次变换可得方程
(
w
1
−
w
2
)
T
x
+
(
b
1
−
b
2
)
=
0
(w_1-w_2)^Tx+(b_1-b_2) = 0
(w1−w2)Tx+(b1−b2)=0，作一次代数替换，令
w
=
(
w
1
−
w
2
)
,
b
=
(
b
1
−
b
2
)
w=(w_1-w_2),b=(b_1-b_2)
w=(w1−w2),b=(b1−b2) 可得
w
T
x
+
b
=
0
w^Tx+b=0
wTx+b=0，这里因为对
y
1
,
y
2
y_1,y_2
y1,y2作了差值，
a
r
g
max
(
x
)
arg \max(x)
argmax(x)不再适用，用
s
i
g
n
(
x
)
sign(x)
sign(x)代替，即：
y
=
s
i
g
n
(
y
1
−
y
2
)
=
{
1
,
w
T
x
+
b
>
0
−
1
,
w
T
x
+
b
≤
0
y = sign(y_1-y_2)=\left\{\begin{matrix} 1&,w^Tx+b> 0\\ -1&,w^Tx+b\leq 0 \end{matrix}\right.
y=sign(y1−y2)={1−1,wTx+b>0,wTx+b≤0所以我们可以看到，二节点的单层全连接层分类模型等价于感知机模型（
w
T
x
+
b
=
0
w^Tx+b = 0
wTx+b=0时分到哪类都是一样的，
a
r
g
max
arg \max
argmax默认分到第
1
1
1 类），区别在于该分类网络多了一倍的参数，其构造的超平面并非
w
1
T
x
+
b
1
=
0
w^T_1x+b_1=0
w1Tx+b1=0或
w
2
T
x
+
b
2
=
0
w^T_2x+b_2=0
w2Tx+b2=0，而是通过节点间计算得到的，在多节点的分类中单个节点的意义比较有限，分离超平面是一个相对问题，而非单个节点所决定的。
以上是二维数据上训练后的结果（损失函数为CrossEntropy，优化器为SGD，学习率固定为0.01，下同）；其中蓝色直线表示节点超平面
w
1
T
x
+
b
1
=
0
w^T_1x+b_1=0
w1Tx+b1=0，绿色直线表示节点超平面
w
2
T
x
+
b
2
=
0
w^T_2x+b_2=0
w2Tx+b2=0，红色直线为（节点间）决策超平面
w
T
x
+
b
=
0
w^Tx+b=0
wTx+b=0。受参数随机初始化的影响，虽然产生了几乎相同的决策超平面，但是节点的超平面却非常不同。
上面总结了 2 2 2个分类的情形，相对而言还是比较简单的，但是到多分类这里就变得更加复杂了。多分类中最简单的模型是 3 3 3分类模型，下面我们将解析 3 3 3分类模型，并推广到大于 3 3 3类的情形。
对于
3
3
3分类模型，输出由
3
3
3个节点组成，
y
1
=
w
1
T
x
+
b
1
y_1 = w^T_1x+b_1
y1=w1Tx+b1，
y
2
=
w
2
T
x
+
b
2
y_2 = w^T_2x+b_2
y2=w2Tx+b2 和
y
3
=
w
3
T
x
+
b
3
y_3 = w^T_3x+b_3
y3=w3Tx+b3，这里有多少分离超平面呢？每
2
2
2个节点构成一个超平面，所以
3
3
3个节点构成
3
3
3个分离超平面，分别为
h
12
=
0
,
h
13
=
0
,
h
23
=
0
h_{12}=0,h_{13}=0,h_{23}=0
h12=0,h13=0,h23=0，其中
h
12
=
(
y
1
−
y
2
)
,
h
13
=
(
y
1
−
y
3
)
,
h
23
=
(
y
2
−
y
3
)
h_{12}=(y_1-y_2),h_{13}=(y_1-y_3),h_{23}=(y_2-y_3)
h12=(y1−y2),h13=(y1−y3),h23=(y2−y3)，同理根据排列组合原理，可以推导出任意节点
n
≥
2
n \geq 2
n≥2构成的超平面数量为：
f
(
n
)
=
C
n
2
=
n
∗
(
n
−
1
)
2
f(n) =C_n^2=\frac{n*(n-1)}{2}
f(n)=Cn2=2n∗(n−1)当我们使用激活函数
s
(
h
)
=
{
1
,
h
>
0
0
,
h
≤
0
s(h)=\left\{\begin{matrix} 1&,h> 0\\ 0&,h\leq 0 \end{matrix}\right.
s(h)={10,h>0,h≤0 去编码超平面所划分的空间，会得到
y
1
=
max
(
y
1
,
y
2
,
y
3
)
⇔
s
(
[
h
12
,
h
13
,
h
23
]
)
=
[
1
,
1
,
0
∨
1
]
y_1=\max(y_1,y_2,y_3)\Leftrightarrow s([h_{12},h_{13},h_{23}])=[1,1,0\vee 1]
y1=max(y1,y2,y3)⇔s([h12,h13,h23])=[1,1,0∨1]
y
2
=
max
(
y
1
,
y
2
,
y
3
)
⇔
s
(
[
h
12
,
h
13
,
h
23
]
)
=
[
0
,
0
∨
1
,
1
]
y_2=\max(y_1,y_2,y_3)\Leftrightarrow s([h_{12},h_{13},h_{23}])=[0,0\vee 1,1]
y2=max(y1,y2,y3)⇔s([h12,h13,h23])=[0,0∨1,1]
y
3
=
max
(
y
1
,
y
2
,
y
3
)
⇔
s
(
[
h
12
,
h
13
,
h
23
]
)
=
[
0
∨
1
,
0
,
0
]
y_3=\max(y_1,y_2,y_3)\Leftrightarrow s([h_{12},h_{13},h_{23}])=[0\vee 1,0,0]
y3=max(y1,y2,y3)⇔s([h12,h13,h23])=[0∨1,0,0]
这里 0 ∨ 1 0\vee 1 0∨1指：0或1，这也意味着，当我们确定空间划分（Space Partitioning）的编码时，我们就能得到概率最大的输出节点。 在大于3个节点时也是同样的道理，不过编码长度会随节点数接近平方增长。下面的图片是超平面将各划分的空间区域编码的一个示例：
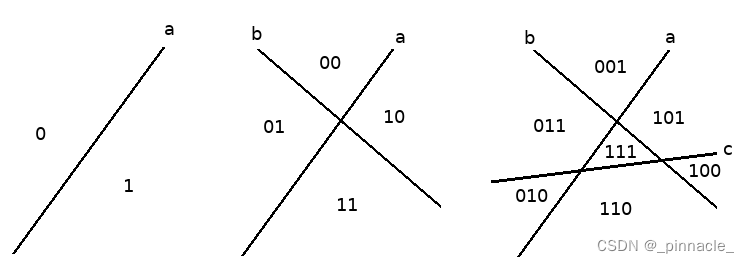
但是我们也注意到这样的编码是不存在的：
s
(
[
h
12
,
h
13
,
h
23
]
)
=
[
0
,
1
,
0
]
s([h_{12},h_{13},h_{23}])=[0,1,0]
s([h12,h13,h23])=[0,1,0]和
s
(
[
h
12
,
h
13
,
h
23
]
)
=
[
1
,
0
,
1
]
s([h_{12},h_{13},h_{23}])=[1,0,1]
s([h12,h13,h23])=[1,0,1]，原因是逻辑不自洽，即：
(
h
12
<
0
,
h
13
>
0
)
⇒
(
y
2
>
y
1
>
y
3
)
⇒
(
y
2
>
y
3
)
⇒
h
23
>
0
(h_{12}<0,h_{13}>0)\Rightarrow (y_2>y_1>y_3)\Rightarrow (y_2>y_3)\Rightarrow h_{23}>0
(h12<0,h13>0)⇒(y2>y1>y3)⇒(y2>y3)⇒h23>0
同理 ( h 12 > 0 , h 13 < 0 ) ⇒ h 23 < 0 (h_{12}>0,h_{13}<0)\Rightarrow h_{23}<0 (h12>0,h13<0)⇒h23<0，这个是节点比较或分类层所带来的特性，意味着3个输出节点产生的3个超平面只产生一个交点，那么在 n > 3 n>3 n>3个节点上的逻辑呢？这个问题留给读者。
模型中还有其他的编码逻辑吗？通过实验归纳我们会发现，节点的超平面也可以参与到编码中，即任意的节点 y i > 0 y_i>0 yi>0能将一半空间中的其他类别数据简单的分离，而因为在 y i > 0 y_i>0 yi>0的空间中可能包含非该类的数据，这个时候需要 y i > y n ∖ i y_i>y_{n\setminus i} yi>yn∖i，那么这个模型中的存在这样的编码逻辑：任意类别数据 x i x_i xi如果可以被单一超平面分离，且对应的 y i y_i yi是 m a x max max输出节点，那么 y i > 0 y_i>0 yi>0 且 y i − y n ∖ i > 0 y_i-y_{n\setminus i}>0 yi−yn∖i>0，即先通过节点划分一半的空间，再在半空间中通过节点间超平面划分。
因为数据并非线性可分，这里需要有一个重要的约束：任意类别数据可以被单一超平面分离，也就是在划分的半空间中存在该类的完整数据。虽然该逻辑是存在的，但模型会受初始化参数与代价函数影响，在边界处理上有权衡，如 y i ≤ 0 y_i\leq0 yi≤0的空间也可能包含该类数据，如上图及下图中个别蓝点存在于 y i ≤ 0 y_i\leq0 yi≤0的区域中，所以以上逻辑中 y i > 0 y_i>0 yi>0更像是一个约束条件，这个约束条件能更好的理解单个节点的逻辑。
以上是二维数据上训练后的结果；其中虚线分别表示节点超平面： y 1 = 0 , y 2 = 0 , y 3 = 0 y_1=0,y_2=0,y_3=0 y1=0,y2=0,y3=0，节点超平面将节点所属类别数据几乎完整划分到半空间中；实线分别表示决策超平面： h y 1 y 2 = 0 , h y 1 y 3 = 0 , h y 2 y 3 = 0 h_{y_1y_2}=0,h_{y_1y_3}=0,h_{y_2y_3}=0 hy1y2=0,hy1y3=0,hy2y3=0，决策超平面将3类数据划分到6个区域中，且每个超平面将两类数据完整分离。
所谓线性区域，特指由线性函数所划分出来的区域，在神经网络中特指超平面所划分的区域。如上图，3个分离超平面（实线）将输入空间划分为了6个线性区域，训练后理想情况下使得每一个区域只包含单个类别的数据，任何输入数据通过获取区域编码就可得到数据的类别。线性区域在深度学习理论中有很多的研究，尤其是在模型复杂度上，线性区域数量能很好的描述模型容量。
对于神经网络而言，最大线性区域数量
f
f
f与输入空间维度
d
d
d、超平面数量
m
m
m的关系为:
f
(
d
,
m
)
=
1
+
m
+
C
m
2
+
.
.
.
+
C
m
d
=
∑
i
=
0
d
C
m
i
f(d,m)=1+m+C_m^2+...+C_m^d=\sum_{i=0}^{d}C_m^i
f(d,m)=1+m+Cm2+...+Cmd=i=0∑dCmi我们带入在2维空间上，超平面数量为3时，可以得到最大可以划分的线性区域数量为
1
+
3
+
3
=
7
1+3+3=7
1+3+3=7，而在单层全连接分类模型中，最大线性区域数量
f
f
f与输入空间维度
d
d
d、节点数量
n
n
n的关系为:
f
(
d
,
n
)
=
∑
i
=
0
d
C
c
n
2
i
f(d,n)=\sum_{i=0}^{d}C_{c_n^2}^i
f(d,n)=i=0∑dCcn2i在有隐藏层的模型中，隐藏层因为激活函数的作用，其节点数量和超平面的关系为
m
=
n
m=n
m=n，最大线性区域的数量计算也较简单，而有隐藏层模型总的线性区域数量计算会不太相同，后续会讨论，其他组合问题可参考 Enumerative Combinatorics 或 Combinatorial Theory的内容。
线性不可分的定义：数据集 D D D存在 n = 2 n=2 n=2类数据，对于任意类别数据 x i x_i xi与其他类别数据 x n ∖ i x_{n\setminus i} xn∖i，存在 ( w , b ) (w,b) (w,b)使得 w T x i + b > 0 w^Tx_i+b>0 wTxi+b>0且 w T x n ∖ i + b ≤ 0 w^Tx_{n\setminus i}+b \leq0 wTxn∖i+b≤0，这时我们称数据集 D D D是线性可分的，反之我们称数据集 D D D是线性不可分的。
这里为什么是 n = 2 n=2 n=2，目前看到的线性可分的定义都是在2类问题上，那就意味着在 n > 2 n>2 n>2类时数据不能被线性划分，但是全连接层的分类模型是可以处理这种 n ≥ 2 n\geq2 n≥2类问题的，且在 n > 2 n>2 n>2时能处理比这个问题稍强的线性不可分情形，即在 w T x i + b > 0 w^Tx_i+b>0 wTxi+b>0的半空间中可以再次划分。
对于多个节点的全连接层模型，模型裁剪与压缩，和有效输入特征的维数有关，所以更多集中在输入特征消减上。
而对于二分类模型，则可以通过前面二分模型的解释里的公式，将 y = ( w 1 − w 2 ) T x + ( b 1 − b 2 ) y=(w_1-w_2)^Tx+(b_1-b_2) y=(w1−w2)Tx+(b1−b2)，作一次代数替换(也即分类模型转换为回归模型)， w = ( w 1 − w 2 ) , b = ( b 1 − b 2 ) w=(w_1-w_2),b=(b_1-b_2) w=(w1−w2),b=(b1−b2) 得到 y = w T x + b y=w^Tx+b y=wTx+b，当 y > 0 时 y>0时 y>0时分为类别一， y ≤ 0 y\leq0 y≤0时分为类别二，这样就可以将模型的参数量减少一半。对于输出为一个或多个二分类节点的模型（如：目标检测模型，分割模型等），通过这种裁剪与压缩方式，其参数量变得和多分类相等，但是却增强了模型的开集识别能力。
其实 B C E W i t h L o g i t s L o s s BCEWithLogitsLoss BCEWithLogitsLoss就是利用这个原理工作的，即模型有多少个类别就输出多少个节点（一个类别时只需要输出一个节点），而不是输出 2 2 2倍类别数的节点， B C E W i t h L o g i t s L o s s BCEWithLogitsLoss BCEWithLogitsLoss显式的带了 s i g m o i d 函数 sigmoid函数 sigmoid函数，所以在模型预测的时候需要带 s i g m o i d sigmoid sigmoid获得概率值，训练时则不用。
通过本篇文章，希望大家能理解单层全连接分类模型的数学原理与编码逻辑，这边文章没有解析多层感知机（MLP），因为多层感知机相对来说会更加复杂其数学原理与编码逻辑，和单层模型有较大的区别，且内容较多，多层感知机的内容将留在下一篇文章分析。代码已开源 DNNexp。
